A novel anti-disturbance fast terminal sliding mode method based on DC-DC boost converter

Bo LIANG; Xiang XU; Rongchao NIU; Hongyu ZHANG; Xuan ZHANG; Yuren LI

doi:10.1051/jnwpu/20254320338

All issues

Volume 43 / No 2 (April 2025)

JNWPU, 43 2 (2025) 338-344

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 2, April 2025


Page(s)		338 - 344
DOI		https://doi.org/10.1051/jnwpu/20254320338
Published online		04 June 2025

JNWPU 2025, 43(2): 338–344

A novel anti-disturbance fast terminal sliding mode method based on DC-DC boost converter

针对DC-DC升压变换器的新型抗干扰快速终端滑模控制方法

Bo LIANG (梁波)¹, Xiang XU (徐翔)¹, Rongchao NIU (牛荣超)², Hongyu ZHANG (张宏宇)¹, Xuan ZHANG (张璇)¹ and Yuren LI (李玉忍)¹

¹ School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
² Xi'an Institute of Applied Optics, Xi'an 710065, China

Received: 14 March 2024

Abstract

In order to stabilize the bus voltage and match the power demand, this paper proposes a new fast terminal sliding mode control strategy to enhance the system's anti-disturbance ability for the DC-DC boost converter. Firstly, a full order sliding mode surface is proposed to ensure finite time convergence of the system state, and an integral type switching control term is proposed to handle large disturbances. Then, perturbation observation is used to calculate system uncertainty which further enhances robustness and reduces chattering. Next, a parameter update mechanism is proposed to calculate the model parameters of the current working point, which helps to improve control performance and enhance flexibility in dealing with different working conditions. Finally, the effectiveness of this method is verified through simulation.

摘要

为了稳定母线电压并匹配功率需求, 以DC-DC升压变换器为研究对象, 提出了一种新的快速终端滑模控制策略, 来增强系统的抗干扰能力。采用一个全阶滑模面保证系统状态的有限时间收敛, 并利用一种积分型切换控制项处理系统扰动; 使用扰动观测器估计系统的不确定性, 从而进一步增强鲁棒性, 减少抖振; 提出了一种参数更新机制计算当前工作点的模型参数, 这有助于改善控制性能并提高应对不同工况的灵活性; 通过仿真验证了所提方法的有效性。

Key words: DC-DC boost converter / parameter estimation / sliding mode control / anti-disturbance

关键字 : DC-DC升压变换器 / 参数估计 / 滑模控制 / 抗干扰

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

随着交通电气化快速发展, DC-DC升压变换器也越来越多地应用在许多能量转换工作中, 如锂电池、燃料电池等。作为直流电力系统的重要组成部分, 变换器的鲁棒性在稳定母线电压、确保电气系统正常运行上至关重要。但是非最小相位行为让升压变换器具有显著的不稳定性, 同时由负载变化或其他因素引起的工作点频繁变化也会影响变换器的控制性能[1–2]。因此研究一种鲁棒控制方法来提高升压变换器的抗干扰能力具有重要意义。

近年来, 学者们提出了许多用于升压变换器的控制策略。在文献[3]中, 将双闭环比例积分控制(PI)用于交错并联升压变换器, 但是它只能确保在额定工作点附近的局部稳定性。在文献[4]中, 提出了一种模糊控制器, 使用Takagi-Sugeno模糊模型来描述系统动力学, 但计算成本较大。文献[5]中还提出了一种反步控制器, 但需要提前将控制对象变换为Brunovsky标准形式, 会涉及到复杂的模型转换和参考轨迹设计。文献[6]中设计了一个内模控制器, 但它需要求解线性扰动模型的逆变换矩阵, 这在实际系统中比较复杂。文献[7]为交错并联升压变换器设计了一种线性有源自抗扰控制器, 但过度简化了控制对象, 增加了观测器的负担。

在各种控制算法中, 滑模控制(sliding mode control, SMC)因对系统参数变化及扰动不灵敏、响应快速等优点而受到广泛关注。文献[8]中为降压转换器提出了线性SMC控制器, 但其跟踪误差渐近收敛到零。文献[9]中为功率转换器开发了终端滑模控制(terminal SMC, TSMC)。通过在滑模面中引入非线性函数, TSMC可以保证误差状态的有限时间收敛。如何确保控制性能并抑制抖振是TSMC应用中的一个挑战。文献[10]将高阶SMC应用于功率转换器, 通过将离散项隐藏到其导数中来减少抖振问题，增强了鲁棒性, 但它需要关于扰动导数的边值信息。在文献[11]中, 通过开发自适应律调整开关增益以减少抖振, 但控制律仍然是离散的。在文献[12]中, 饱和函数被用来代替符号函数, 尽管获得了更平滑的控制信号，减少了抖振问题, 但这是以牺牲鲁棒性为代价的。在这种情况下，扰动估计技术也被集成到了控制器中。系统扰动由观测器估计, TSMC主要用于参考跟踪[13–14]。在文献[13]中, 针对降压转换器提出了具有延迟估计技术的快速终端滑模控制器(fast terminal SMC, FTSM)。在文献[14]中, 有限时间观测器被用作TSM控制器的前馈补偿项, 实验结果显示出更好的跟踪性能。然而, 文献[13–14]倾向于选择较小的开关增益减少抖振。当发生较大的外部扰动时, 仅利用观测器估计所有系统的不确定性将导致缓慢的动态响应。此外, 基线TSM定律中模型参数的不准确也会在一定程度上影响系统的稳定性。

综合上述问题, 本文提出了一种将扰动估计和参数更新机制相结合的新型FTSM律。与现有的基于观测器的FTSM采用标称模型并定义总扰动不同, 本文开发了一种参数更新机制来计算当前工作点的模型参数。除了正常工作条件下的负载或输入电压变化外, 还可以识别开路故障条件下的模型失配。在实时更新模型的基础上, 设计了一个全阶滑模流形来解决奇异性问题, 设计了积分切换控制项来产生连续信号并减少抖振。最后, 使用扰动观测器来补偿系统的不确定性。由于通过参数更新机制识别外部扰动引起的模型失配, 大大减少了需要观测器估计的不确定性, 从而提高了鲁棒性和收敛速度。

1 变换器动态模型

1.1 变换器拓扑

为了便于说明, 选择两相交错并联升压变换器(TIBC), 如图 1所示。该拓扑包含2个电感器L₁, L₂, 2个开关管S₁, S₂, 2个二极管D₁, D₂, 1个电容C和1个等效负载R_L。v_i为电源电压, v_o为输出电压, i_L₁, i_L₂为电感电流, d₁, d₂为2个开关管的占空比, 初始相位δ₁和δ₂间隔π。为简化计算, 假设两相电路的电感值相同, 即L₁=L₂=L。

假设变换器总是工作于连续导通模式, 并忽略电路中的损耗, 则变换器的增益为

式中, V_o, V_i, D分别是状态变量v_o, v_i, 以及d₁, d₂的平均值。

变换器的动态模型为

图1

变换器拓扑

1.2 等效电压控制策略

本文采用如图 2所示的级联控制方法, 重点研究负责电压跟踪以及抑制扰动的外环控制器, 因此电流控制器采用Super-Twisting滑模控制, 设计为

式中：i_{L_ref}是参考电感电流；α₁, β₁是控制器增益。

电流环的控制频率通常远高于电压环, 因此在设计电压控制环时可以认为电感电流被严格控制到参考值。在理想的滑模下(ṡ_k=s_k=0), 根据(2)~(3)式, 电流环的等效控制为

将(4)式代入(2)式中的电压动态方程, 可得电感电流和输出电压之间的动态模型为

基于(5)式, 变换器的平衡点为

再结合图 2, 2个电流控制器接收相同的参考电流值, 因此(5)式可以改写为

(7) 式是参考电感电流和输出电压的非线性函数关系, 这给控制设计和性能分析带来了困难。为了简化分析和便于控制设计, 假定u为电感电流参考值, y为输出电压, 则(7)式改写为

式中：a=1/R_LC; b=2V_i/CV_o；w是系统的总扰动, 包含非最小相位行为和参数a, b的模型失配。

图2

TIBC的双闭环控制策略

2 总体控制策略

2.1 FTSM设计

对于功率变换器, 控制目标是将(8)式中的实际输出y调节到其参考y_r。将控制误差定义为e_v=y-y_r, 建立一阶滑模面为

式中: k₁>0;0 < α < 1。建立理想滑动s_v=0后, 根据(9)式, 控制误差如(10)式所示。

通过求解(10)式, 可以得到e_v及其导数的收敛轨迹如(11)~(12)式所示。

式中, e_v(0)是控制误差的初始值。

由(11)式可知, 当系统状态轨迹满足s_v=0时, 控制误差将会在有限时间t_s内收敛到平衡点e_v=ė_v=0。

FTSM控制系统的收敛包含到达阶段s_v→0和e_v→0沿着(10)式滑动的阶段。对应的2个控制项是切换控制项u_sw和等效控制项u_eq。因此, FTSM方法定义为

当状态轨迹接近s_v=0时, 等效控制项u_eq可以将其限制在滑模面上。结合(8)式, 将s_v=0代入(9)式, 并考虑ẏ_r=0, u_eq可求解为

切换控制法迫使系统轨迹向s_v=0移动。对于传统的SMC, 切换控制是离散的, 而当状态轨迹接近s_v=0时, 切换项的不连续性将导致抖振问题, 所以利用积分型控制律来平滑控制信号并减少抖振, 并将切换控制项定义为

2.2 基于扰动观测器的FTSM控制

本节主要研究系统不确定性的估计。假定参考输出恒定, 将(8)式代入(9)式, 得到滑动流形s_v为

将(14)~(16)式代入(17)式, 有

根据(18)式, 当阶跃扰动发生时, 假设w>0, s_v将满足

状态轨迹会在t_s=w/k_s中达到s_v=0, 这代表积分型切换控制项(16)式可以补偿系统扰动, 但抖振、鲁棒性和收敛速度之间存在着矛盾。一方面, 从(19)式中可知, 需要高控制增益k_s确保对大扰动的适应和收敛速度, 但另一方面, 需要低控制增益k_s减少抖振问题。因此, 利用非线性扰动观测器(NDO)估计(8)式中的扰动项w, 然后在等效控制项(15)式中消除干扰估计。NDO如(20)式所示。

式中: ŵ是w的扰动估计；z是辅助变量；p(*)是辅助函数；l_d是观测器增益。

如果满足(21)式, NDO就可以渐近估计总扰动。

将NDO的估计误差定义为e_r=w-ŵ, 基于(20)式和(21)式, e_r的导数为

求解(22)式后, 可得NDO的误差动力学为

对于阶跃扰动, 存在ẇ(t>0)=0, 误差动力学将渐近收敛到ė_r=e_r=0;对于时变扰动, e_r将渐近收敛到e_r=ẇ/l_d。等效控制项重写为

根据(24)式, (18)式可写为

根据(25)式, 李雅普诺夫函数的导数为

再根据(23)式, 假定e_r(0)>ẇ/l_d, 则e_r的上限可以表示为e_r≤(ẇ+δ)/l_d, 其中δ>0并且满足δ≪ε。

因此确保系统稳定的k_s范围为

δ值在实际应用中难以识别, 为明确表现出扰动观测器的影响, 确保系统稳定性的一个充分条件是

这证明利用NDO可以在不增加控制增益k_s的情况下有效地提高FTSM的收敛速度, 且有助于进一步减少抖振。

2.3 模型参数更新机制

上文的设计过程中, 从(8)式开始计算模型参数a, b, 所以总扰动w会包含a, b的模型失配和变换器的非最小相位行为。而不准确的模型参数a, b可能会影响到等效控制项。另一方面, 由于通常选择较低的控制增益k_s减少抖振, 干扰主要由观测器来补偿, 增加了观测器的估计负担。高的观测器增益l_d可以提高收敛速度, 降低误差e_r, 但也会放大测量噪声。

因此本文提出了一种基于稳态模型的模型参数更新机制, 通过测量变量i_{L_k}, d_k来更新当前工作点的相关参数a, b, 其中核心思想是连续执行(5)~(8)式。有了这个机制, 就能利用精确的模型参数设计FTSM控制律和观测器, 同时减少观测器估计的总扰动值。

根据(2)式, TIBC的稳态模型为

由(8)式可知, a=1/(R_LC), 受负载R_L的影响, 这也是功率变换器的主要外部扰动。将(29)式代入(8)式, 将R_L替换为测量值, 得到

对于模型参数b=2V_i/(CV_o), 实际系统中通常不测量输入电压。将(29)式代入(8)式, 模型参数b近似为

另外, (31)式在开路故障工况中同样适用。当其中某一相电路断开时, 相应的占空比将为d_k=1, 且由(31)式计算出的值是初始值的一半。

所提出的FTSM方法详细框图如图 3所示。可以看出，与(14)式相比，参数更新机制不需要额外的传感器，并且能以较低的计算成本计算精确的模型参数。

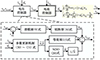图3

提出的FTSM方法框图

3 测试分析

为了验证所提出的FTSM方法有效性, 在MATLAB/Simulink中搭建了变换器系统模型和级联控制器。测试的TIBC详细参数如表 1所示。控制器参数选择为k₁=200, α=0.5, k_s=500, l_d=500, 电流内环参数整定为α₁=0.05, β₁=30。

在此基础上, 测试了参数更新机制对控制系统的影响。先对具有固定模型参数的FTSM控制器进行了测试, 然后根据(30)~(31)式进行参数辨识, 并在0.3 s后实时更新观测器中的模型参数和等效控制律。固定模型参数a, b，根据(8)式中的标准操作点计算, 取a=100, b=1 200。另外, 将k_a和k_b定义为a, b的估计值和标准值的比值。

首先, 将输入电压设置为v_i=20+4sin(40πt), 负载电阻设置为14.4 Ω, 仿真结果如图 4所示。可以看出, 在0.3 s之前, 参数更新机制不工作, 此时输出电压范围为62.9~65.0 V。在0.3 s之后, 模型参数自动更新。当输入电压变化时, 变化率k_a几乎不变, 在0.95~1.06的范围内；而b与输入电压有关, 因此变化率k_b在0.62~1.02的范围内。当参数更新机制工作后, 输出电压仅在63.8~64.2 V的范围内波动, 电压扰动显著减小。

其次, 对系统正常工况下的负载扰动进行测试。负载电流设为i_o=6+2sin(40πt), 仿真结果如图 5所示。在0.3 s之前, 参数更新机制并不工作, 输出电压范围为62.4~65.5 V。在0.3 s之后, 模型参数自动更新。变化率k_a在0.46~1.36的范围内, 因为a的值与等效负载电阻有关。从(8)式中可以看出, b的值与负载电阻无关, 因此图 5中的变化率k_b几乎不变。在0.3 s之后, 输出电压范围变为63.3~64.5 V, 表明变换器鲁棒性明显增强。

假设发生开路故障, 只有一路正常工作, 且负载电流设置为i_o=6+2sin(40πt), 此时仿真结果如图 6所示。可以看出, 模型参数的标准值与实际值相差很大, 因此0.3 s之前的电压扰动大于图 5中的正常工况, 在61.2~66.5 V之间。0.3 s后, 模型参数更新机制工作, 变化率k_a在0.79~1.68之间。这是因为此时TIBC作为传统的升压变换器工作, 转换效率较低, 并且产生较高的占空比d_k以满足负载功率。0.3 s后, 输出电压为63.3~64.6 V, 与正常工况一致。因此, 参数更新机制增强了系统在单相开路故障工况下的灵活性。

最后, 基于dSPACE实时仿真系统搭建了直流变换器的实验测试平台, 硬件电路参数与控制器参数与仿真测试中相同。考虑到直流变换器的应用情况, 重点测试了2种FTSM方法对负载扰动的抑制能力, 负载电流在2.5~5 A之间周期变化, 实验结果如图 7~8所示。

如图 7~8所示, 当负载电流在2.5~5 A之间周期性变化时, 2种FTSM方法对应的输出电压均可被调节至输出参考值64 V, 然而电压瞬态过程有所不同。当负载电流升高时, 基于观测器的固定参数FTSM方法电压跌落为7.4 V, 恢复时间为21 ms; 对于本文提出的自适应参数FTSM方法, 电压跌落为5.5 V, 恢复时间为9 ms。当负载电流下降50%时, 基于观测器固定参数FTSM方法电压超调为8.5 V, 恢复时间为23 ms; 对于本文提出的自适应参数FTSM方法, 电压超调为6.5 V, 恢复时间为12 ms。因此, 参数更新机制的使用增强了直流变换器对负载扰动的抵抗能力。

表1

变换器参数

图4

在v_i=20+4sin(40πt)下的仿真结果

图5

在标准工况下i_o=6+2sin(40πt)的仿真结果

图6

在开路故障工况下i_o=6+2sin(40πt)的仿真结果

图7

固定参数FTSM方法对应的实验结果

图8

自适应模型参数的FTSM方法对应的实验结果

4 结论

为了提高DC-DC升压变换器的抗干扰能力, 本文提出了一种新型的FTSM控制器。与现有的利用固定模型进行控制的系统不同, 本文的主要贡献之一是设计了一种参数更新机制, 该机制可以通过测量每个采样周期的状态变量更新模型参数。利用实时更新的实际模型参数建立等效控制项, 并将积分型切换控制项与观测器相结合, 抑制了抖振问题。测试结果表明, 该参数更新机制可以提高FTSM在不同工况下的灵活性和鲁棒性。

References

HEGAZY O, MIERLO J V, LATAIRE P. Analysis, modeling, and implementation of a multidevice interleaved DC/DC converter for fuel cell hybrid electric vehicles[J]. IEEE Trans on Power Electronics, 2012, 27(11): 4445–4458. [Article] [Google Scholar]
JANABI A, WANG B. Switched-capacitor voltage boost converter for electric and hybrid electric vehicle drives[J]. IEEE Trans on Power Electronics, 2020, 35(6): 5615–5624. [Article] [Google Scholar]
KABALO M, PAIRE D, BLUNIER B, et al. Experimental evaluation of four-phase floating interleaved boost converter design and control for fuel cell applications[J]. IET Power Electronics, 2013, 6(2): 215–226. [Article] [Google Scholar]
BEID S, DOUBABI S. DSP-based implementation of fuzzy output tracking control for a boost converter[J]. IEEE Trans on Industrial Electronics, 2014, 61(1): 196–209. [Article] [Google Scholar]
XU Q, JIANG W, BLAABJERG F, et al. Backstepping control for large signal stability of high boost ratio interleaved converter interfaced DC microgrids with constant power loads[J]. IEEE Trans on Power Electronics, 2020, 35(5): 5397–5407. [Article] [Google Scholar]
KOBAKU T, PATWARDHAN S C, AGARWAL V. Experimental evaluation of internal model control scheme on a DC-DC boost converter exhibiting nonminimum phase behavior[J]. IEEE Trans on Power Electronics, 2017, 32(11): 8880–8891. [Article] [Google Scholar]
ZHUO S, GAILLARD A, XU L, et al. Extended state observer-based control of DC-DC converters for fuel cell application[J]. IEEE Trans on Power Electronics, 2020, 35(9): 9923–9932. [Article] [Google Scholar]
WANG B, MA G, XU D, et al. Switching sliding-mode control strategy based on multi-type restrictive condition for voltage control of buck converter in auxiliary energy source[J]. Applied Energy, 2018, 228: 1373–1384. [Article] [Google Scholar]
KOMURCUGIL H. Adaptive terminal sliding-mode control strategy for DC-DC buck converters[J]. ISA Trans, 2012, 51(6): 673–681. [Article]. [Google Scholar]
SHI S, XU S, GU J, et al. Global high-order sliding mode controller design subject to mismatched terms: application to buck converter[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2019, 66(12): 4840–4849. [Article] [Google Scholar]
SHEN X, LIU J, ALCAIDE A M, et al. Adaptive second-order sliding mode control for grid-connected npc converters with enhanced disturbance rejection[J]. IEEE Trans on Power Electronics, 2022, 37(1): 206–220. [Article] [Google Scholar]
LIU J, VAZQUEZ S, WU L, et al. Extended state observer-based sliding-mode control for three-phase power converters[J]. IEEE Trans on Industrial Electronics, 2017, 64(1): 22–31. [Article] [Google Scholar]
WANG Z, LI S, LI Q. Discrete-time fast terminal sliding mode control design for DC-DC buck converters with mismatched disturbances[J]. IEEE Trans on Industrial Informatics, 2020, 16(2): 1204–1213. [Article] [Google Scholar]
WANG Z, LI S, LI Q. Continuous nonsingular terminal sliding mode control of DC-DC boost converters subject to time-varying disturbances[J]. IEEE Trans on Circuits and SystemsⅡ: Express Briefs, 2020, 67(11): 2552–2556. [Article] [Google Scholar]

All Tables

表1

变换器参数

In the text

All Figures

	图1 变换器拓扑
In the text

	图2 TIBC的双闭环控制策略
In the text

	图3 提出的FTSM方法框图
In the text

	图4 在v_i=20+4sin(40πt)下的仿真结果
In the text

	图5 在标准工况下i_o=6+2sin(40πt)的仿真结果
In the text

	图6 在开路故障工况下i_o=6+2sin(40πt)的仿真结果
In the text

	图7 固定参数FTSM方法对应的实验结果
In the text

	图8 自适应模型参数的FTSM方法对应的实验结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] HEGAZY O, MIERLO J V, LATAIRE P. Analysis, modeling, and implementation of a multidevice interleaved DC/DC converter for fuel cell hybrid electric vehicles[J]. IEEE Trans on Power Electronics, 2012, 27(11): 4445–4458. [Article] [Google Scholar]

[2] JANABI A, WANG B. Switched-capacitor voltage boost converter for electric and hybrid electric vehicle drives[J]. IEEE Trans on Power Electronics, 2020, 35(6): 5615–5624. [Article] [Google Scholar]

[3] KABALO M, PAIRE D, BLUNIER B, et al. Experimental evaluation of four-phase floating interleaved boost converter design and control for fuel cell applications[J]. IET Power Electronics, 2013, 6(2): 215–226. [Article] [Google Scholar]

[4] BEID S, DOUBABI S. DSP-based implementation of fuzzy output tracking control for a boost converter[J]. IEEE Trans on Industrial Electronics, 2014, 61(1): 196–209. [Article] [Google Scholar]

[5] XU Q, JIANG W, BLAABJERG F, et al. Backstepping control for large signal stability of high boost ratio interleaved converter interfaced DC microgrids with constant power loads[J]. IEEE Trans on Power Electronics, 2020, 35(5): 5397–5407. [Article] [Google Scholar]

[6] KOBAKU T, PATWARDHAN S C, AGARWAL V. Experimental evaluation of internal model control scheme on a DC-DC boost converter exhibiting nonminimum phase behavior[J]. IEEE Trans on Power Electronics, 2017, 32(11): 8880–8891. [Article] [Google Scholar]

[7] ZHUO S, GAILLARD A, XU L, et al. Extended state observer-based control of DC-DC converters for fuel cell application[J]. IEEE Trans on Power Electronics, 2020, 35(9): 9923–9932. [Article] [Google Scholar]

[8] WANG B, MA G, XU D, et al. Switching sliding-mode control strategy based on multi-type restrictive condition for voltage control of buck converter in auxiliary energy source[J]. Applied Energy, 2018, 228: 1373–1384. [Article] [Google Scholar]

[9] KOMURCUGIL H. Adaptive terminal sliding-mode control strategy for DC-DC buck converters[J]. ISA Trans, 2012, 51(6): 673–681. [Article]. [Google Scholar]

[10] SHI S, XU S, GU J, et al. Global high-order sliding mode controller design subject to mismatched terms: application to buck converter[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2019, 66(12): 4840–4849. [Article] [Google Scholar]

[11] SHEN X, LIU J, ALCAIDE A M, et al. Adaptive second-order sliding mode control for grid-connected npc converters with enhanced disturbance rejection[J]. IEEE Trans on Power Electronics, 2022, 37(1): 206–220. [Article] [Google Scholar]

[12] LIU J, VAZQUEZ S, WU L, et al. Extended state observer-based sliding-mode control for three-phase power converters[J]. IEEE Trans on Industrial Electronics, 2017, 64(1): 22–31. [Article] [Google Scholar]

[13] WANG Z, LI S, LI Q. Discrete-time fast terminal sliding mode control design for DC-DC buck converters with mismatched disturbances[J]. IEEE Trans on Industrial Informatics, 2020, 16(2): 1204–1213. [Article] [Google Scholar]

[14] WANG Z, LI S, LI Q. Continuous nonsingular terminal sliding mode control of DC-DC boost converters subject to time-varying disturbances[J]. IEEE Trans on Circuits and SystemsⅡ: Express Briefs, 2020, 67(11): 2552–2556. [Article] [Google Scholar]