| Issue |
JNWPU
Volume 43, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 305 - 315 | |
| DOI | https://doi.org/10.1051/jnwpu/20254320305 | |
| Published online | 04 June 2025 | |
Study on influence of dense medium on impact pressure of detonation waves subjected to contact blasts
接触爆炸下密实介质对爆轰波垂直入射压力的影响规律研究
1
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China
2
Hubei Aerospace Flight Vehicle Institute, Wuhan 430040, China
Received:
17
April
2024
In order to investigate the buffering effect of the different dense medium on the shock waves in the contact blasts, a dimensional analysis method by using the zero-pressure sound speed of dense medium was proposed. The present approach led to the establishment of a dimensionless relationship describing the influence of the impedance on the vertical incident pressure. To validate this methodology, the classical detonation wave propagation theory was employed to calculate the pressure values of shock waves propagating into typical dense medium. Additionally, finite element analysis software was used to simulate the initiation processes of three types of explosives with different dense medium acting as buffer layers. Explicit simulations accurately reproduced the reflection of shock waves/rarefaction waves within the explosives after passing through medium with varying impedances, with the error in pressure value calculations being controlled below 8%. Combining these results with the assumptions made in dimensional analysis and a large dataset, the specific form of the dimensionless relationship was established. Subsequently, a dimensionless model for pressure of shock waves incident on dense medium, based on the explosive density and detonation velocity, was developed. By comparing the predicted with the experimental results, it was found that the error was below 10%, thus confirming the accuracy of the model in engineering applications. Moreover, since obtaining the zero-pressure sound impedance is much easier than that by using the Hugoniot relation, the present model greatly simplifies the computational complexity and provides the useful references for predicting the pressure values incident on novel dense medium.
摘要
为了研究接触爆炸时不同密实介质对于爆轰波缓冲作用的影响规律, 提出用密实介质的零压体声速进行量纲分析的方法, 建立了阻抗影响垂直入射压力的无量纲关系式。为了验证所提方法的准确性, 通过经典爆轰波传播理论分析计算传入典型密实介质中冲击波的压力值; 利用有限元分析软件模拟了不同密实介质作为缓冲层的3种炸药起爆过程。显式仿真中通过压力云图的方式展现了爆轰波经过不同阻抗的介质后反射回炸药中的冲击波/稀疏波情况, 两者压力值计算结果的误差在8%以内。从而结合验证了量纲分析时的假设条件, 通过大量数据点确立了无量纲关系式的具体形式。拟合了通过炸药密度和爆速的预测爆轰波入射密实介质压力的无量纲数学模型, 经过与实验结果进行对比, 误差在10%以内, 验证了建立的预测模型在工程应用上的准确性。并且由于零压声阻的获取难度远远小于Hugoniot关系, 因此建立的预测模型大大节约了计算时间, 同时对其入射新型密实介质的压力值预测能够提供一定的参考。
Key words: contact blasts / dimensional analysis / pressure change / numerical simulation / predictive model
关键字 : 接触爆炸 / 量纲分析 / 压力变化 / 数值仿真 / 预测模型
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
提高破片战斗部的毁伤能力是当前高效毁伤领域的研究热点, 受到了世界各国广泛关注和大力研究。现阶段破片战斗部的研究中常常将破片视为刚体[1]。但是实际上由于爆轰波产生的超压过高, 破片会发生变形行为[2]。当破片材料脆性较强时, 甚至会发生断裂破碎行为[3–4]。而破片的变形和断裂破碎行为, 会影响破片的初速, 甚至导致提前释能从而影响终点毁伤能力[5–7]。
在破片与战斗部装药间加覆一层密实介质作为缓冲层以降低破片所受载荷, 可有效防止破片在爆炸驱动过程中发生碎裂, 破片的破碎程度越低, 其飞散速度和毁伤能力越高[8–11]。因此为了保证破片的结构完整性和初速, 应该选择合适的密实介质作为缓冲层材料。
前期相关学者研究发现, 破片式战斗部中采用不同的缓冲层不会改变破片的变形机制, 但是能影响破片的变形程度, 其主要通过调节冲击波波形和压力值大小实现[9, 12]。相比高冲击阻抗密实介质, 低冲击阻抗密实介质能更好地减小施加在破片上的压力。但是前期研究没有对密实介质影响入射压力的规律进行总结, 从而找出影响入射压力值的主要因素与其影响的相关特性。除此之外, 冲击阻抗是一个随波速变化的值, 因此现阶段对炸药和密实介质的冲击阻抗大小判断比较困难, 基本都采用对比密度的方式进行粗略比较[13–14]。
本研究提出采用零压体声速进行量纲分析的方法, 讨论了零压体声速阻抗和垂直入射压力的对应关系, 通过经典理论和仿真验证了假设条件, 同时确立了关系式的具体形式。最终建立了预测典型炸药入射不同阻抗密实介质内的压力值的数学模型, 与相关实验数据进行对比, 从而验证了模型的适用性与准确性。本文研究能够为破片战斗部缓冲材料的选择以及基于新型炸药的密度和爆速预测入射压力提供参考。西北工业大学学报第43卷第2期孟元沛, 等:接触爆炸下密实介质对爆轰波垂直入射压力的影响规律研究
1 量纲分析
密实介质在接触爆炸载荷作用下的响应涉及多个物理量, 进行量纲分析时, 决定密实介质内的冲击波压力pm的物理量包含以下3个方面。
1) 炸药的物理量参数, 包括炸药密度ρe、炸药爆速De、炸药绝热指数γ;
2) 爆轰波入射时的物理量参数, 包括爆轰波入射密实介质的角度φ;
3) 密实介质的物理量参数, 包括介质密度ρm0、介质的Hugoniot参数am和bm。
各物理量的基本量纲幂次如表 1所示。
基于上述分析, 密实介质内的冲击波压力pm与各物理量之间的关系函数可写为
取炸药密度ρe和炸药爆速De为基本量, (1)式可化为
当讨论爆轰波垂直入射的压力时, 可以忽略φ的影响, 即
参考炸药的爆轰波Chapman-Jouguet[13]面上产物压力pC-J,如(4)式所示, 增加无量纲量γ为基本量, 进行简单变换可化简(2)式为无量纲关系(5)式。
事实上, 当无量纲表达式化简为(5)式, 对关系式左右两边进行拟合时, 需要考虑的因素仍然较多, 现阶段进行具体表达式的拟合时缺乏直接的表达形式, 得到其对应关系较为困难。因此需要对(5)式进行分析。
密实介质的相关基本物理属性参数还包括
式中,C, K, G, E, Cl和Ct分别表示固体的零压体声速、体积模量、剪切模量、弹性模量、纵波声速和横波声速。其中零压体声速包含了体积模量、剪切模量、弹性模量和密度的影响。密实介质内冲击波传播速度如(10)式所示。由(10)式可知am实际上可以被视为在零压时(或极低压力时)的声速, 这与零压体声速的概念吻合(即C=am)。即相对来说, 零压体声速可以表征冲击波速的相对大小。
结合文献[13], 发现D是一个随um不断变化的值, 并且不同介质的am, bm变化规律不明显。这给判断炸药和密实介质的阻抗关系常来了阻碍, 同时使无量纲表达式变得复杂。
综合以上2个因素, 同时基于简化表达式的初衷, 选择忽略bm的影响, 并且参考炸药冲击阻抗ρeDe(Ie)的概念, 引入零压体声速阻抗Im(Im=amρm0, 下文简称零压声阻)对(5)式进行简化, 得到
由(11)式可知, 只要确定了密实介质的零压声阻, 得到Im/Ie和pm/pC-J两者之间无量纲表达式的具体形式, 原理上便可以预估传入该密实介质的压力值大小。
通过上述量纲分析建立的无量纲关系式, 需要解决3个问题: ①是否可以采用零压声阻Im近似代替固体的冲击阻抗进行反射波类型的判断;②忽略bm的影响后, 零压体声阻Im(amρm0)与pm之间是否存在对应关系;③建立Im/Ie和pm/pC-J两者无量纲表达式的具体形式并验证其工程应用。
密实介质内爆轰波初入射压力值的量纲幂次系数
2 垂直入射压力计算理论模型
第1节忽略bm建立了Im/Ie和pm/pC-J两者的对应关系, 为了解决问题①, 本节首先介绍垂直入射密实介质的经典理论模型。
接触爆炸下, 爆轰产物向密实介质中飞散时, 在密实介质中会透射冲击波, 但根据密实介质的不同, 爆轰产物中会反射回冲击波或者稀疏波, 这取决于密实介质和炸药的冲击阻抗比[12–13]。
因此基于爆轰波的Chapman-Jouguet(C-J)理论[13], 首先建立爆轰波C-J面上产物的初始参数为
式中,pC-J, ρC-J, uC-J和cC-J分别为炸药产生爆轰波在C-J点的压力、密度、质点速度和声速; γ是炸药的气体膨胀系数; ρe是炸药装药的初始密度; De是炸药爆速。
2.1 反射波为稀疏波
当与炸药接触的密实介质冲击阻抗小于炸药时, 爆轰产物中反射回稀疏波。为了解决第1节中问题①,本研究采用零压声阻代替密实介质的冲击阻抗进行判断。当与炸药接触的密实介质零压声阻小于炸药时,爆轰产物中反射回稀疏波。稀疏波传入爆轰产物之后, 介质中的粒子受到扰动, 从而发生相对运动, 导致粒子之间的间距增大, 从而降低其平均密度。而爆轰产物中压力定义为单位面积上的力, 粒子的分散会导致粒子之间的碰撞频率减少, 并减小了单位面积上施加的力, 从而使压力降低。
此时, 炸药与密实介质分界面处的质点速度为[13]
式中,um和pm分别为分界面运动速度和压力值。
另一方面, 由冲击突跃条件可知冲击波阵面后介质的运动速度为
式中:pm0和vm0分别是爆轰波未与密实介质作用时密实介质内的压力和比容。
联立(12)~(14)式可得反射回爆轰产物为稀疏波时, 密实介质中的压力和速度。
2.2 反射波为冲击波
当与炸药接触的密实介质的零压声阻大于炸药的冲击阻抗时, 密实介质内和爆轰产物将透射形成冲击波, 在爆轰产物中反射回冲击波。爆轰产物中粒子在冲击波前沿受到极端压缩,粒子密度增加, 同时粒子之间的高速运动和碰撞会导致动能增加。这些因素使得爆轰产物内压力比C-J压力更高。
此时, 炸药与密实介质分界面处的质点速度为
反射波为冲击波的情况不会影响冲击波阵面后介质的运动速度, 因此其速度也如(15)式所示。
联立(12)、(14)和(15)式可得反射回爆轰产物为冲击波时, 密实介质中的压力和速度。
3 计算模型的建立
3.1 图解法理论模型
图解法的关键是确立以压力p和速度u为坐标系并且初始状态为(pC-J, uC-J)的爆轰产物的Hugoniot方程, 进而画出其相应曲线。对于爆炸产物中反射稀疏波的情况, 对(13)式进行以(pC-J, uC-J)为始点的改写,如(16)式所示。
而爆轰产物反射冲击波的情况需要对(15)式进行以(pC-J, uC-J)为始点的改写,如(17)式所示。
最后根据爆轰产物中反射波的情况, (16)式或(17)式联立密实介质的Hugoniot方程(10)式, 可以通过图解法交点求得初入参数
式中:ρm0为密实介质的密度; am和bm是密实介质的Hugoniot的2个参数。
表 2~3所示是上文理论所需的不同密实介质参数[13–14]。
所需炸药参数表
所需密实介质参数表
3.2 数值仿真模型
数值模拟可以在一定程度上再现密实介质在爆炸加载下的动态响应及变形过程。本文主要使用商业有限元仿真软件LS-DYNA对密实介质在接触爆炸下的过程进行数值模拟。LS-DYNA是一款非常强大的显式动力学有限元分析软件, 在模拟高速、非线性、瞬态加载情况下具有高度可靠性, 能够准确地预测结构在极端载荷下的响应, 并且提供了丰富的后处理功能, 能够直观地显示仿真结果, 并支持动画显示, 便于分析密实介质和炸药中波的传播过程。
为保证爆轰波垂直入射缓冲层的条件, 简化后的1/4战斗部仿真模型如图 1所示, 由战斗部装药、密实介质和空气域组成。采用TrueGrid编程网格模型, 从而最大程度地避免由于网格质量问题导致的仿真收敛性和稳定性的问题。同时为提高分析效率, 并最大可能保证垂直入射条件, 引入基于LS-DYNA软件的二维数值计算方法设置炸药和密实介质[6, 9, 12]。
战斗部装药采用TNT、RDX和8701炸药, 其二维尺寸为半径20 mm的1/4圆形, 采用*MAT_HIGH_EXPLOSIVE_BURN和*EOS_JWL关键字设置炸药基本参数, 这些关键字能定义炸药燃烧速率模型、能量输出模型和压力响应模型, 并且预测燃烧产生的气体压力波的传播, 并考虑到密度、温度和化学反应等因素。
密度介质二维尺寸为内径20 mm,外径30 mm的1/4圆环。密实介质和战斗部装药之间设置0.01 mm的空隙, 这样可以避免几何上的干涉或碰撞, 防止错误的力传递造成非预期的应力和变形分布,避免刚度矩阵的奇异性或收敛困难。密实介质依据不同阻抗的材料特性采用*MAT_JOHNSON_COOK和*MAT_ELASTIC_PLASTIC_HYDRO关键字来预测材料在爆炸加载条件下的行为。
空气域和炸药相邻, 其二维尺寸为内径20 mm, 外径45 mm的1/4圆环。空气域的本构模型采用*MAT_NULL。空气域的设置能够将固体和流体之间的相互作用转移到空气域上, 通过空气域定义固体和流体之间的传递条件从而简化问题并降低计算复杂性。
对于空气域和战斗部装药采用ALE网格, 其相比于传统的欧拉方法具有更好的适应性和精确性, 特别适用于模拟自由面流动、液固耦合、多介质流动等需要考虑大变形和移动边界的问题。对于密实介质采用Lagrange网格, 设置流固耦合对爆炸驱动过程进行数值模拟研究。利用这一方法, 由于材料物质在网格中可以流动, 因此不存在单元畸变问题。
 |
图1 数值仿真模型 |
4 结果与讨论
4.1 图解法的计算结果
由于聚苯乙烯、环氧树脂、酚醛树脂的零压声阻均小于炸药的冲击阻抗,所以爆轰产物中反射回稀疏波。而铝、钛、铜、钨的零压声阻均大于炸药的冲击阻抗,因此爆轰产物中反射回冲击波。
图 2所示是图解法计算结果。
图 2a)为pm < pC-J时密实介质中的p-u曲线, 对应2.1节中反射稀疏波的情况; 图 2b)为pm>pC-J时密实介质中的p-u曲线, 对应2.2节中反射冲击波的情况。炸药根据其产生的爆轰波C-J压力排序为: TNT < RDX < 8701;密实介质根据零压声阻排序为: 聚苯乙烯 < 环氧塑料 < 酚醛树脂 < 铝 < 钛 < 铜 < 钨。图 2中炸药(实线)和密实介质(虚线)的交点即为该炸药产生的爆轰波传入对应密实介质冲击波的压力值和质点速度。
图 2中炸药和密实介质均有交点, 由此验证了采用密实介质的零压声阻代替冲击阻抗进行判定的适用性, 其相比用密度对比的方式更为精准。为了更清晰地展示爆轰波在分界面的变化情况(稀疏波或者冲击波), 以及对压力值的影响, 对数值模拟的结果进一步讨论。
 |
图2 图解法p-u曲线图 |
4.2 数值仿真的计算结果
通过二维可视化方式, 显示有限元仿真得到的炸药和密实介质中各个位置的压力分布情况。图 3和图 4所示分别是8701炸药传入2种不同的典型密实介质2.2 μs和2.3 μs的压力云图。在数值计算中, 特别是在高频振荡或高应变率的冲击波等问题中, 由于离散化误差、数值格式和网格分辨率等因素影响, 可能会出现数值解的振荡或不稳定情况。这些振荡和不稳定行为会影响数值解的准确性和可靠性。因此在如图 3~4所示的压力云图中, 将爆轰波的强间断面进行了数值耗散, 通过引入人为的耗散效应来抑制数值解中的振荡和不稳定行为。除此之外这样的方式也有利于直接观测分界面前后冲击波的透反射情况。
图 3a)和图 4a)是8701炸药传入聚苯乙烯密实介质前后0.1 μs的压力云图, 云图颜色表示了不同位置的压力大小。云图红色程度越高, 则压力值越高, 反之越低。如图 3a)所示,在爆轰波传入聚苯乙烯前,其压力值为32.51 GPa。当爆轰波传入聚苯乙烯后压力值变为了20.81 GPa,2.3 μs时刻压力云图如图 4a)所示。同时云图中炸药产生了压力值较低的波形, 这是因为炸药的阻抗比聚苯乙烯的阻抗高, 所以在炸药中反射回稀疏波, 压力云图中的情况对应了2.1节中理论分析的结果。
图 3b)和图 4b)是8701炸药传入铜密实介质前后0.1 μs的压力云图。图 3a)和图 3b)有相同的压力云图, 这是因为此时爆轰波仍在炸药传播, 不涉及跨介质传播, 同时证明了仿真的可重复性。而如图 4b)所示的压力云图中, 在爆轰波传入密实介质后, 在炸药中产生了压力值高于C-J值的波形, 这是由于炸药阻抗小于密实介质, 因此在炸药中反射回冲击波, 导致其压力升高。图 4b)所示的结果对应了2.2节中理论分析的结果。
表 4所示是根据图解法和数值仿真得到的计算结果, 依据炸药类型进行分类, 并且为了对比传入密实介质中的压力值, 同时给出了炸药定常爆轰的C-J理论压力值。
对比仿真压力值和理论计算的误差, 控制在8%以内, 通过仿真一定程度上直观再现了反射波为稀疏波或者冲击波的情况。从而再一次验证了采用密实介质的零压声阻代替冲击阻抗进行判断的适用性。
基于爆轰波基本理论及数值模拟结果,采用零压声阻代替冲击阻抗对密实介质的影响较小,尤其对炸药爆轰产物中反射波的波形及压力值的变化影响不显著。因此问题①得到有效验证。
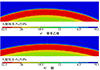 |
图3 2.2 μs时刻压力云图 |
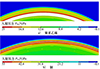 |
图4 2.3 μs时刻压力云图 |
理论和仿真计算结果对比表
4.3 密实介质声阻对传入其内压力值的影响分析
为了更清晰地研究不同炸药和密实介质对于爆轰波入射压力值的影响, 图 5给出了密实介质内压力计算结果曲线, 展示了压力值的变化趋势, 其中Im表示密实介质材料的零压阻抗, T和S分别代表理论和仿真结果。
如图 5a)所示, 对比同一种炸药产生的爆轰波传入不同密实介质的压力值, 其压力值随着密实介质阻抗的增大而增大。如图 5b)所示, 综合对比不同炸药产生的爆轰波入射同一种密实介质的压力, 其压力值主要随着炸药的C-J压力增大而增大。图 5b)结合表 4结果, 得到: 当密实介质零压声阻小于炸药冲击阻抗时, 爆轰波传入密实介质的压力小于炸药的C-J压力; 反之, 传入密实介质的压力将大于炸药的C-J压力。两者均呈现正相关的趋势。综合图 5中不同炸药产生的爆轰波传入对于不同密实介质的压力值分析, 不论在分界面产生稀疏波或者冲击波, 对于其压力值正相关的趋势没有影响, 即密实介质的阻抗越大, 爆轰波传入密实介质的压力值越大; 炸药的C-J压力越大则传入密实介质的压力值越大。
因此,采用密实介质的零压声阻代替冲击阻抗后,其与压力值之间呈现出非线性特征的对应关系。
 |
图5 密实介质入射压力计算结果图 |
5 预测模型的建立
5.1 对应关系的拟合
基于上述分析, 综合炸药和密实介质的阻抗差异情况, 依据不同密实介质的密度和冲击波Hugoniot参数(文献[14]附录), 得到3种典型炸药入射后的压力值。根据得到的压力值数据点, 可以拟合出如图 6所示的曲线图。
3种炸药的爆轰波入射压力值和零压声阻均遵循指数关联的规律, 即压力值与密实介质零压声阻之间的非线性关系一定程度上可以用一个指数函数来描述, 如(19)式所示。
式中: 当A0值较大时, 曲线整体上移; 当A0值较小时, 曲线整体下移; B的大小决定了压力值随指数增长的快慢程度。
(19) 式中的参数数值会根据具体炸药类型有所不同。TNT、RDX和8701炸药分别对应的参数值如表 5所示。
大量数据点与拟合关系(19)式的拟合程度由表 6展现。其中相关系数均十分接近1说明相关性很强, 决定系数均十分接近1说明拟合程度很好。均方根误差展示了拟合曲线和数据点的平均偏差程度, 考虑到由于炸药本身问题导致的实际压力值大小差异, 其误差值较小。
爆轰波从炸药传播到不同冲击阻抗的密实介质时, 部分冲击能量会被反射、透射或吸收。这些反射、透射和吸收效应受到密实介质的冲击阻抗特性影响, 产生非线性效应。压力值和密实介质零压声阻之间的非线性效应随着两者阻抗差异变大而变大, 这种非线性响应, 造成炸药入射密实介质压力的预测模型呈指数增加的形式。
显然,当量纲分析时忽略bm, 这种非线性效应的对应关系仍然存在, 图 6的指数型曲线和(19)式的指数型关系式中可以证明。因此, 大量数据点和拟合结果验证了第1节中问题②。
综上所述, 可以根据具体的炸药和密实介质情况, 利用建立的模型预测相应的压力值。并且根据拟合结果的(19)式, 第1节问题③中所需建立的关系式形式被确定。基于此指数形式, 下一节将讨论和建立无量纲关系式。
 |
图6 3种典型炸药入射密实介质内压力拟合曲线图 |
3种典型炸药入射密实介质的模型参数
拟合程度参数表
5.2 无量纲关系式的建立
通过5.1节得到的3种炸药在不同密实介质中压力值的预测模型, 证明了此非线性的指数形式的适用性。因此综合炸药和密实介质的阻抗比和压力比, 结合(11)式和图 7进一步拟合得到其无量纲理论预测模型为
式中:Ie为炸药的密度与爆速的乘积;Im为密实介质的阻抗;pm为爆轰波传入密实介质后密实介质内的压力。
对3种典型炸药进行拟合, 以零压声阻的选取范围为基准, 所建模型在阻抗比为0.04~7.77时能够预测不同炸药产生的爆轰波入射不同密实介质时压力值情况。图 7中放大图显示的是阻抗比介于0~0.6之间的数据点与预测模型的对应情况。
 |
图7 不同炸药的爆轰波入射不同密实介质时的归一化模型 |
5.3 试验验证
为了验证模型的准确性和对不同炸药密实介质组合的适用性, 将本文法与现有研究中不同炸药在不同密实介质内由接触爆炸产生的压力值进行比对。基于本文建立预测模型的条件限制, 验证预测模型时选用的文献试验工况需要满足以下条件: ①炸药空气中起爆;②炸药发生稳定爆轰;③需要与密实介质进行直接接触爆炸。
基于上述条件选择文献[15–23]的试验结果进行验证。具体对比情况如表 7和图 8所示。其中文献[15–22]均有试验得到的直接结果。而文献[23]中, 其实验得到了冲击波在介质内不同位置的压力实验值后, 其进行该密实介质的衰减公式总结, 得到了密实介质内由接触爆炸产生的初入射压力值。
建立的无量纲预测模型采用文献中的炸药和密实介质计算压力值,与其结果误差值在10%以内,具有一定的工程应用价值。因此第1节中的问题③得到验证。建立的预测模型准确性和对其他炸药的适用性较强,同时其计算过程可以被大大简化,相对于经典理论所需的炸药及密实介质的各种参数而言(其中零压声阻的获取难度远远小于Hugoniot的获取难度),(20)式仅需炸药的冲击阻抗和密实介质的零压声阻。经过表 7和图 8的试验验证后,其可以推广应用到现有炸药以预测其在密实介质中的传播特性。
预测模型与文献结果对比情况表
 |
图8 预测模型与现有研究结果对比情况图 |
6 结论
提出用密实介质的零压体声速进行量纲分析的方法, 初步建立了压力值和阻抗之间的对应关系。接着通过一维冲击波理论分析建立了接触爆炸下密实介质中初始冲击波压力的计算模型, 通过仿真建模与计算结果进行对比, 两者曲线趋势一致, 误差在8%以内, 仿真结果再现了爆轰波经过不同阻抗的介质后反射回炸药中的冲击波/稀疏波情况。两者结合验证了零压声阻代替冲击阻抗方法的适用性, 最终基于大量数据点建立了预测炸药入射密实介质的压力值的无量纲模型, 通过试验结果进行了验证。得到的具体结论如下:
1) 可以采用零压体声速阻抗近似代替冲击阻抗进行量纲分析。由于冲击波速与波后粒子速度相关, 相对于密度或者冲击阻抗, 采用零压声阻可以较为简单且相对准确地判断爆轰波传入密实介质时反射的稀疏波还是冲击波, 进而对其采用不同的计算理论求得压力值。
2) 接触爆炸作用下密实介质中初始冲击波压力与其零压声阻呈正相关, 密实介质的零压声阻越高, 则传入密实介质的压力值越高。两者呈现非线性的指数相关特性, 与炸药冲击阻抗的差异越大, 压力值的增大趋势越小。
3) 建立了爆轰波垂直入射不同阻抗密实介质时冲击波压力的预测模型。经过对比验证,与试验结果的误差控制在10%以内。该模型可以根据密实介质零压声阻直接预测不同炸药接触爆炸时产生的压力值。
4) 由于零压声阻的获取难度远远小于材料的Hugoniot关系,因此所建模型大大简化了计算过程和难度。对于预测新型炸药在新型材料中的冲击波压力具有一定的指导作用。
References
- WANG Shushan. Termainal Effectology[M]. 2nd ed. Beijing: Science Press, 2019 (in Chinese) [Google Scholar]
- HUER J. A coalescence criterion for porous single crystals[J]. Journal of the Mechanics and Physics of Solids, 2019, 124: 505–525. [Article] [Google Scholar]
- MENG Y P, HE Y, GUO L, et al. Influence of metal on the far-exploding surface on fragment deformation behavior under contact explosion[J]. Journal of Applied Physics, 2024, 136: 145902. [Article] [Google Scholar]
- TANG Jiaojiao, LIANG Zhengfeng, QU Kepeng, et al. Correlation between the mechanical properties of tungsten alloy fragments and fracture behavior driven by detonation loading[J]. Chinese Journal of Explosives & Propellants, 2020, 43(3): 293–297 (in Chinese) [Google Scholar]
- YANG Y S, WANG C T, MENG Y P, et al. Recent progress on impact induced reaction mechanism of reactive alloys[J]. Defence Technology, 2024, 37: 69–95. [Article] [Google Scholar]
- MA Yue, HE Yong, WANG Chuanting, et al. Response behavior of double layer tungsten fragments under detonation loading[J]. Journal of Northwestern Polytechnical University, 2022, 40(4): 819–828. [Article] (in Chinese) [Google Scholar]
- CHENG Xingwang, WANG Jinxiang, TANG Kui, et al. Analysis on the initial velocity field of a multi-layer spherical fragment driven by explosion[J]. Journal of Vibration and Shock, 2020, 39(16): 129–134 (in Chinese) [Google Scholar]
- YU Qingbo, WANG Haifu, JIN Xueke, et al. Influence of buffer material on explosive driven of reactive fragment warhea[J]. Transactions of Beijing Institute of Technology, 2013, 33(2): 124–126 (in Chinese) [Google Scholar]
- MA Y, HE Y, WANG C T, et al. Influence of lining materials on the detonation driving of fragments[J]. Journal of Mechanical Science and Technology, 2022, 36(3): 1337–1350. [Article] [Google Scholar]
- DENG X M, WU H J, YANG X. Preformed fragment velocity distribution of elliptical cross-section projectile[J]. Latin American Journal of Solids and Structures, 2022, 19: 423. [Article] [Google Scholar]
- CHEN Chuang, HAO Yongping, YANG Li, et al. Research on double layer medium gap test and analysis of shock initiation characteristics of acceptor explosive[J]. Acta Armamentarii, 2017, 38(10): 1957–1964. [Article] (in Chinese) [Google Scholar]
- MENG Y P, HE Y, WANG C T, et al. The effect of surface electroplating on fragment deformation behavior when subjected to contact blasts[J]. Materials, 2023, 16(15): 5464. [Article] [Google Scholar]
- ZHANG Shouzhong. Explosion and shock dynamics[M]. Beijing: The Publishing House of Ordnance Industry, 1993 (in Chinese) [Google Scholar]
- ZHANG Baoping, ZHANG Qingming, HUANG Fenglei. Detonation Physics[M]. Beijing: The Publishing House of Ordnance Industr, 2009 (in Chinese) [Google Scholar]
- XU Seng, LIU Dabin, PENG Jinhua, et al. Study on the shock wave attenuation of the booster charge in the PMMA gap[J]. Chinese Journal of High Pressure Physics, 2010, 24: 431–437. [Article] (in Chinese) [Google Scholar]
- ZHANG Baoping, JIANG Chunlan, HONG Bing, et al. Experim ental Investigations on the oblique reflection of detonation waves at the explosive-metal interface[J]. Transactions of Beijing Institute of Technology, 1992, 12: 26–33 (in Chinese) [Google Scholar]
- LIU Haoquan, HE Yangyang, ZHANG Yangyi, et al. Numerical analysis of the antiexplosion anchored effects of linedtunnel under dynamic loads[J]. Explosive Materials, 2009, 38: 1–8 (in Chinese) [Google Scholar]
- LI Shuyan, WANG Zaicheng, MAO Liang, et al. Characterization and mechanical behavior of Ti/Al nanoscaled multilayers[J]. Ordnance Material Science and Engineering, 2020, 43: 43–49 (in Chinese) [Google Scholar]
- WANG Quan, ZHANG Jinyuan, GUO Ziru, et al. Research of explosion pressure on the lnterface between emulsion explosive and steel target[J]. Journal of Anhui University of Science and Technology Company, 2022, 42: 66–70 (in Chinese) [Google Scholar]
- CHEN Chuang, WANG Xiaoming, LI Wenbin, et al. Influence of multilayered media impedance matching on explosion interruption effect[J]. Journal of Vibration and Shock, 2014, 33: 105–110 (in Chinese) [Google Scholar]
- JIANG Xibo, RAO Guoning, XU Sen, et al. Numerical simulation and experimental research on shock wave attenuation properties in PMMA[J]. Journal of Nanjing University of Science and Technology, 2012, 36: 1059–1064 (in Chinese) [Google Scholar]
- HOU Haizhou, PENG Jinhua, HU Yiting. Experimental study of shock wave attenuation properties in phenolic cotton fabric material[J]. Initiators and Pyrotechnics, 2016, 2: 13–16 (in Chinese) [Google Scholar]
- WANG Zuoshan, LIU Yucun, ZHENG Min, et al. Study on the attenuating mbdel of detonation shock wave in the PMMA gap[J]. Journal of Basic Science and Engineering, 2001, 9: 316–319 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 数值仿真模型 |
| In the text | |
 |
图2 图解法p-u曲线图 |
| In the text | |
 |
图3 2.2 μs时刻压力云图 |
| In the text | |
 |
图4 2.3 μs时刻压力云图 |
| In the text | |
 |
图5 密实介质入射压力计算结果图 |
| In the text | |
 |
图6 3种典型炸药入射密实介质内压力拟合曲线图 |
| In the text | |
 |
图7 不同炸药的爆轰波入射不同密实介质时的归一化模型 |
| In the text | |
 |
图8 预测模型与现有研究结果对比情况图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


