| Issue |
JNWPU
Volume 43, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 488 - 495 | |
| DOI | https://doi.org/10.1051/jnwpu/20254330488 | |
| Published online | 11 August 2025 | |
Experimental research of pulsation pressure and hydrodynamic noise at the bow of underwater vehicle
水下航行器艏部脉动压力及水动力噪声试验研究
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
2
Key Laboratory of Unmanned Underwater Vehicle Technology, Northwestern Polytechnical University, Xi'an, 710129, China
3
Soaring Key Laboratory, Northwestern Polytechnical University, Xi'an 710129, China
Received:
13
July
2024
The design of the bow of the underwater vehicle affects its hydrodynamic performance, and a better design can reduce the direct impact of water on the bow and thus reduce the hydrodynamic noise of the underwater vehicle. In the towing pool, five models with different bow shapes were tested for the first time using pulsation pressure sensors and hydrophone to synchronize the pulsation pressure and hydrodynamic noise at different speeds and flow positions. The experiment results show that the velocity and bow shape have significant effects on the pulsation pressure and hydrodynamic noise. The higher the speed, the higher the instability of the fluid flow and the higher the intensity of the pulsation pressure; the bow shape has a critical value between "sharp" and "rounded", which makes the peak of the pulsation pressure most backward and shows a lower hydrodynamic noise.
摘要
水下航行器艏部的设计影响其在水中的流体动力性能, 较好的线型设计可以减少水对艏部的直接冲击从而降低航行器水动力噪声。在拖曳水池中, 针对5种具有不同艏部线型的航行器模型, 使用脉动压力传感器和水听器对不同速度、不同流向位置的脉动压力和水动力噪声进行了同步测试。试验结果表明, 航行速度及艏部线型对脉动压力和水动力噪声均有显著影响。速度越大, 流体流动的不稳定性增加, 脉动压力强度增大; 艏部线型在"尖锐"和"圆钝"之间存在临界值, 使得脉动压力峰值的位置最靠后, 表现出较低的水动力噪声。
Key words: underwater vehicle / bow shape / pulsation pressure / hydrodynamic noise
关键字 : 水下航行器 / 艏部线型 / 脉动压力 / 水动力噪声
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
水下航行器的声隐身性能是其生存和执行作战任务的首要目标。航行器水下辐射噪声主要包括机械噪声、螺旋桨噪声和水动力噪声。在低速航行时, 水动力噪声的数值比机械振动噪声和螺旋桨噪声要低, 但是随着航行速度的提高, 水动力噪声在总噪声中的比重会迅速增加, 水动力噪声问题变得尤为突出。水动力噪声由航行器周围湍流边界层扰动、壁面脉动压力以及流固耦合作用导致的结构振动共同引起[1]。
目前有很多针对水下航行器流场和声场的研究。在流场研究中, 美国泰勒中心[2]对SUBOFF潜艇模型进行了试验, 得到了速度、压力和雷诺应力等试验数据, 为近年来的仿真研究提供了对照基准。Suh等[3]使用数值仿真手段, 分别采用雷诺平均Navier-Stokes方程(Reynolds-averaged Navier-Stokes equations, RANS)和分离涡模拟(detached eddy simulation, DES)研究了SUBOFF潜艇模型周围的流动, 通过对比得到, 利用DES模拟出的流场更加真实。Qu等[4]采用大涡模拟(large eddy simulation, LES)结合浸没边界法(boundary data immersion method, BDIM)分析了潜艇围壳周围马蹄涡、发卡涡和项链涡的拓扑结构, 揭示了不同涡结构的形成机制。姜宜辰等[5]研究了附体对潜艇阻力及尾部伴流场的影响, 结果表明附体的存在会导致黏压阻力和伴流场不均性显著增加, 稳定翼对桨盘面半径内伴流场不均匀性的影响较大, 围壳主要影响桨盘面半径外伴流场不均匀性。
在声场研究中, 于连杰等[6]基于Ffowcs Williams-Hawkings方程预报线性噪声, 使用直接体积分方法预报非线性噪声, 分析了SUBOFF远场和近场声压频域分布特征, 并结合双网格方法降低计算量。俞孟萨等[7]通过仿真模拟过渡区的声辐射, 建立了水下航行器艏部低噪声线型的设计方法, 艏部声呐部位自噪声的计算结果与试验结果相比, 在3 000 Hz以上频段偏差小于3 dB。吕世金等[8]对水下航行体艏部水动力噪声和平头端面直径之间的关系进行了研究, 结果表明端面直径增加1倍, 水动力噪声增加约5 dB, 故采用减小端面直径的方法降低艏部水动力噪声。
在水下航行器流场和声场研究的基础上, 学者们从降低阻力、改善伴流场以及降低噪声等角度出发, 开展了附体外形、附体与主艇体连接形式和艏部线型优化设计等研究。李芳等[9]基于仿生学将座头鲸尾鳍前缘波浪结构应用于翼型外形设计, 达到了较好的降噪效果。王曦晖等[10]研究了不同围壳形状对流噪声的影响和抑制作用, 发现通过在围壳前缘加装填角可以有效抑制流噪声, 总声压级可以降低9.3 dB。Moonesun等[11]从阻力最小化的角度探讨了潜艇艏部的最佳线型, 对半球型艏部、圆锥形艏部和椭圆型艏部进行了仿真模拟, 从阻力系数、总阻力等角度分析了不同形状的优劣。除了以上基于计算流体动力学(computational fluid dynamics, CFD)的研究手段, 开展相关试验也是一个重要的研究方式。Javadi等[12]进行了2种不同艏部形状潜艇模型的试验测试, 讨论了艏部形状对阻力的影响, 结果表明当弗劳德数相同时, Tango型模型的波浪阻力明显小于标准艏形, 然而当弗劳德数较高时, 艏形效应较小, 总阻力取决于潜艇长度和排水量。
通过上述文献可以看出, 水下航行器外形的优化设计是一个重要的方向, 其目的为改善水动力性能、减少阻力和降低噪声。当航行器在水中航行时, 其几何形状会影响水流分布, 艏部一般承受着较大的压力; 其次, 艏部表面经历层流、转捩和湍流3个状态, 转捩区域和湍流区域存在强烈的涡流运动和脉动压力, 这些涡运动和脉动压力是流噪声的来源, 对航行器艏部的声呐基阵产生影响。本文将采用试验的方法, 对5个具有不同艏部线型的航行器模型进行测试, 分析航行速度及艏部线型对艏部表面脉动压力的影响, 揭示脉动压力峰值位置与艏部噪声之间的关系。
1 试验模型和设备
1.1 试验模型
模型由艏部、平行中段、艉部以及连接杆四部分组成, 如图 1所示。由于研究聚焦于艏部, 模型的艉部进行了简化处理, 仅起导流作用。模型通过连接杆和拖车连接, 在试验过程中, 仅替换模型艏部, 平行中段、艉部和连接杆保持不变。中段长500 mm, 艉部长500 mm, 连接杆长度为210 mm。模型艏部采用回转体外形, 最大直径为500 mm, 不同艏部线型示意如图 2所示。模型材质为铝合金, 厚度为8 mm, 部分位置进行了加厚处理以提高模型的强度, 模型总质量约为135 kg。
 |
图1 试验模型组成 |
 |
图2 模型艏部线型示意图 |
模型艏采用双参数椭圆线型, 符合
式中: x为模型外形横坐标; y为模型外形纵坐标; D为模型最大直径; Df为模型艏部端面直径; Lh为艏部长度; n和m为线型参数。
各线型的具体参数如下。
线型1: n=6.397 3, m=1.939 9;
线型2: n=3.450 9, m=1.939 2;
线型3: n=2.533 7, m=1.825 3;
线型4: n=2.124 5, m=1.785 1;
线型5: n=2.396 9, m=1.223 1。
在试验之前, 通过仿真计算证明了平行中段及艉部简化的合理性, 航速为3.08 m/s时, 线型1~5的阻力值依次为54.8, 52.8, 50.59, 49.79, 49.29 N, 符合流线型艏部的阻力值更小的规律。
1.2 试验设备
脉动压力和噪声同步测试试验在西北工业大学拖曳水池实验室完成。该水池长170 m, 宽7 m, 深6 m, 最大试验速度为7.20 m/s。本试验的测试系统由脉动压力传感器、水听器、信号放大器、采集系统和计算机等组成。
1) 脉动压力传感器。型号为PCB 106B50, 该传感器灵敏度为72.5 mV/kPa, 谐振频率大于40 kHz, 量程为182 dB。
2) 水听器。型号为B & K 8103, 灵敏度为30 μV/Pa, 并经过了单独校准, 可保证在很宽的频率范围内具有平坦的频率响应。
3) 放大器。仅在噪声采集通道使用。
4) 采集系统。采样频率为65 536 Hz。
较“钝”的线型1和较“尖”的线型5, 受限于加工工艺, 同时考虑到传感器分布均匀性, 安装了6个脉动压力传感器, 线型2~4安装了7个脉动压力传感器, 首先在艏部顶端安装1个传感器, 然后在流向方向上依次进行安装。在距离艏部顶端150 mm处安装水听器。脉动压力传感器和水听器安装位置示意图如图 3所示。试验流程如图 4所示。
 |
图3 脉动压力传感器和水听器安装示意图 |
 |
图4 试验流程 |
2 试验测试
分别对5个艏部线型不同的模型进行了3.08, 4.11, 5.14, 6.17 m/s航速下的水下拖曳试验, 每个速度重复3次, 保证数据的可靠性和可重复性。不同航速下试验测试照片如图 5所示。在每次测试之前, 均进行水面消波处理和背景噪声采集。
 |
图5 不同航速下实验测试照片 |
3 试验结果讨论
3.1 脉动压力试验结果与讨论
脉动压力是由于水流运动的强烈紊动在物体表面产生的围绕在时均压强上下的脉动量。水下航行器在流体介质中运动时, 物体边界层由层流状态发展为湍流状态, 在时间和空间上均有随机变化的不稳定现象, 这个过程称之为转捩。在失稳的过程中, 流动特性如速度、压力等物理量也会发生显著的不规则变化。基于此, 通过对脉动压力的测量和分析, 可以了解和判断流动是否进入了转捩区域。
图 6为线型1模型在速度为3.08 m/s下3个测量点的脉动压力时域信号, 3个测量点的Res是以距离艏部顶点的轴线长度s为特征长度的雷诺数, 图 6a)中测量点与艏部顶点的距离为93 mm, 图 6b)中为173 mm, 图 6c)中为362 mm。可以看到脉动压力的幅值在图 6a)非常小, 在图 6b)有一个突然增大, 到图 6c)有一定程度下降, 但幅值仍高于图 6a)。
 |
图6 3.08 m/s下3个测量点脉动压力的时间历程 |
胡成行等[13]在风洞中探测锥体边界层转捩, 得到了相似的规律。可以推测这3个位置分别属于层流区域、转捩区域和湍流区域。脉动压力在层流区域很小, 到转捩区域有一个剧烈的变化, 之后迅速衰减发展到湍流区域。在模型表面, 脉动压力迅速增加的过程, 体现出流体流动结构在此区域变得更加复杂和混乱, 与转捩过程中的非定常现象相关, 特别是高频振荡和湍流斑的猝发。
线型1模型在速度为3.08 m/s下不同监测点脉动压力的频谱曲线如图 7所示。脉动压力的频域特征用脉动压力级Gp表示, 定义为
 |
图7 3.08 m/s下3个测量点脉动压力的频域曲线 |
式中：pref为基准声压, 水中的基准声压为1×10-6 Pa; G(f)为脉动压力功率谱密度函数。
由图 7可以看出, 脉动压力遵循转捩区域(B点)谱级最高, 往湍流发展的区域(C点)谱级降低, 层流区(A点)域谱级最低的规律。
脉动压力尤其是测量得到的近场脉动压力, 是流噪声的主要成分, 分别计算3个测量点的总脉动压力级, 结果如表 1所示。转捩区域(B点)的总脉动压力级比湍流区域(C点)的总脉动压力级大9.63 dB, 说明了在转捩区域会产生更大的流动激励源。水下航行器艏部一般安装声呐基阵, 为了避免转捩引起的自噪声影响艏部声呐的工作, 通常通过调整艏部线型延迟转捩。
3.08 m/s下3个位置处总脉动压力级
由于脉动压力是随时间发生周期性或非周期性变化的一种压力现象, 通过统计分析, 可以更加准确地描述脉动压力的变化规律。本文定义脉动压力的均方根值PRMS表示测量信号的强度, 有
式中: pi是数据集中的第i个数据; N是数据集中的数据总数。
将5个不同线型的模型在不同速度下的脉动压力强度进行对比分析, 结果如图 8所示。可以看到随着速度的增加, 脉动压力的强度增加, 航速从3.08~4.11 m/s, 艏部顶点脉动压力强度增加7%;航速从5.14~6.17 m/s, 脉动压力强度增加22%。这是由于随着速度的增大, 雷诺数增大, 流体流动的不稳定性增加, 旋涡和湍流等现象更加显著所导致。对于线型3, 可以看到不同速度下均在x/Lh=0.37达到了峰值, 在3.08 m/s和4.11 m/s下, x/Lh=0.46和x/Lh=0.56的脉动压力强度大于5.14 m/s和6.17 m/s。这是由于随着速度的增大, 艏部转捩区前移, 对于3.08 m/s和4.11 m/s, 流场在x/Lh=0.46和x/Lh=0.56仍处于转捩区域, 脉动压力强度大, 而对于5.14 m/s和6.17 m/s, 流场在x/Lh=0.46和x/Lh=0.56已经从转捩过渡到湍流区域, 脉动压力强度比转捩区小。受限于脉动压力传感器的测量面无法做到无限小, 试验不能判断出具体的转捩点位置, 但是根据脉动压力的统计值, 可以得到3.08~6.17 m/s速度范围内, 转捩发生的区域范围。
 |
图8 不同速度下的脉动压力变化曲线 |
图 9为不同线型的模型在速度为3.08 m/s下脉动压力强度变化曲线, 图 10为不同线型脉动压力强度峰值点位置。可以发现脉动压力峰值的位置随着艏部线型的变化而变化, 但两者不是简单的线性关系。直观地表述, 从线型1~3, 随着艏部线型变“尖”, 峰值出现的位置向后移, 但是随艏部线型往更“尖”的趋势发展(线型3~5), 脉动压力出现的峰值又开始向前移动。这说明了在“尖”和“钝”中间, 存在一个临界线型, 使得脉动压力峰值出现的位置最靠后。
 |
图9 3.08 m/s下不同艏部线型模型脉动压力强度变化曲线 |
 |
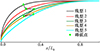图10 不同线型的脉动压力强度峰值点位置 |
3.2 噪声试验结果和讨论
本节研究艏部水动力噪声和艏部线型之间的关系。图 11为线型1模型速度为3.08 m/s时和拖车静止时的噪声测量结果, 拖车静止时的噪声视为背景噪声, 用“BG”表示。从图 11中可以看出, 模型噪声幅度明显高于背景噪声, 信噪比较高, 故在后续分析中不再考虑背景噪声的影响。纵坐标用声压级LSP表示, 计算公式为
 |
图11 线型1噪声和背景噪声测量结果 |
式中：pref为基准声压；S(f)为声压功率谱密度函数。
图 12为线型1模型在不同速度下的噪声测量结果。在100~1 500 Hz范围内, 模型噪声幅度基本保持不变。大于1 500 Hz时, 随着频率的增大, 噪声幅度逐渐降低, 符合水下噪声在高频衰减较快的规律。图 12展示了3.08~6.17 m/s速度下的噪声频谱曲线, 可以看到随着速度增加, 噪声幅值也逐渐增加。上节分析提到, 速度增加脉动压力的强度也增加, 但是两者在频域上的表现略有不同, 脉动压力在8 500 Hz后出现衰减的趋势, 噪声在1 500 Hz开始衰减, 引起差异的原因主要是试验所测得的噪声并不是单纯的流噪声, 还包括了由于模型振动引起的流激噪声。图 13~16为其他4个线型的模型在不同速度下的噪声频谱, 可以看到和线型1模型的变化规律基本相似, 在此不再赘述。
 |
图12 线型1不同速度下的噪声频谱 |
 |
图13 线型2不同速度下的噪声频谱 |
 |
图14 线型3不同速度下的噪声频谱 |
 |
图15 线型4不同速度下的噪声频谱 |
 |
图16 线型5不同速度下的噪声频谱 |
表 2为不同线型的模型在3.08, 4.11, 5.14, 6.17 m/s下的总声压级, 不同线型模型在速度为3.08 m/s时的1/3倍频程如图 17所示。通过对比可以看到在不同的速度工况下, 线型3的总声压级最小。但是在频域范围内线型3并不是全频段均比其他线型幅值小, 在50~250 Hz范围内, 线型3的幅值和其他线型相差不大, 在250~600 Hz, 线型3的幅值最低, 在1 000 Hz以上, 线型3和线型5的幅值低于其余3个线型。其次, 线型3和线型5的1/3倍频程分布较为一致, 总声压级较为接近, 在脉动压力的分析中, 线型3和线型5的脉动强度最高点位置也较接近。由此可以得到噪声和转捩点的位置有关, 转捩点越靠后, 艏部噪声越低。
不同线型的总声压级 dB
 |
图17 3.08 m/s速度下不同线型的1/3倍频程 |
对比不同速度下各线型的噪声变化, 可以发现不同的线型对速度变化的敏感度不同, 线型1在3.08~6.17 m/s航速下, 最大总声压级与最小总声压级的差值为7.66 dB, 线型2为6.55 dB, 线型3为5.53 dB, 线型4为4.37 dB, 线型5为3.75 dB。线型1对速度的变化最为敏感, 这种敏感性是由试验装置还是艏部线型曲率引起的还需要进一步研究。
4 结论
本文采用拖曳水池对水下航行器模型艏部的脉动压力及水动力噪声进行测试试验, 分析了不同航速下不同艏部线型的脉动压力和水动力噪声变化规律, 从转捩点位置和低噪声的角度考虑, 线型3为最优线型, 并得到以下结论。
1) 在同一线型下, 随着速度的增加, 艏部顶点处的脉动压力强度增加幅值最大, 航速从3.08~4.11 m/s, 艏部顶点脉动压力强度增加5%~7%;航速从5.14~6.17 m/s, 脉动压力强度增加16%~22%。航行器在相对较高的航速下, 脉动压力强度的变化更剧烈。
2) 对于艏部线型, 转捩点的区域并不是线型越尖越往后, 在“尖锐”和“圆钝”的艏部线型之间存在临界值, 使得脉动压力峰值的位置最靠后, 在本试验中线型3为最优线型。
3) 水动力噪声声压级随着来流速度的增大而增大, 不同线型对速度变化的敏感度不同, 线型1在3.08~6.17 m/s速度下, 水动力噪声最大总声压级和最小总声压级差值为7.66 dB, 对速度变化的敏感性最大。
4) 给定速度下, 对于不同的艏部线型, 转捩点越靠后, 艏部噪声越低, 越有利于艏部声呐的工作。
References
- TANG Weilin, YU Mengsa, WANG Bin. Hydrodynamic noise theory[M]. Beijing: Science Press, 2019 (in Chinese) [Google Scholar]
- GROVES N, HUANG T, CHANG M. Geometric characteristics of DARPA(defense advanced research projects agency) SUBOFF models(DTRC model numbers 5470 and 5471)[M]. Maryland: David Taylor Research Center, 1989 [Google Scholar]
- SUH S, PARK I. Numerical simulation of the flow around the suboff submarine model using a des method[J]. Journal of the Society of Naval Architects of Korea, 2021, 58(2): 73–83 [Google Scholar]
- QU Y, WU Q, ZHAO X, et al. Numerical investigation of flow structures around the darpa suboff model[J]. Ocean Engineering, 2021, 239: 109866 [Google Scholar]
- JIANG Yichen, LI Yongkun, WANG Qing, et al. Research on influence of appendage position on wake field of underwater vehicleJournal of Huazhong Univerity Science and Technology, 2021, 49(5): 32–37 (in Chinese) [Google Scholar]
- YU Lianjie, YANG Luchun, ZHAO Weiwen, et al. Numerical prediction study of nonlinear hydrodynamic noise for SUBOFF submarine[J]. Shipbuilding of China, 2023, 64(4): 229–239 (in Chinese) [Google Scholar]
- YU Mengsa, LYU Shijin, WU Yongxing. An acoustic designing method of low noise profile for for-body of underwater vehicle[J]. Chinese Journal of Hydrodynamics, 2002, 17(5): 529–537 (in Chinese) [Google Scholar]
- LYU Shijin, MIAO Jinlin, ZHANG Xiaowei. Prediction method of hydrodynamic self-noise and design of low noise bow profile for underwater high speed vehicle[J]. Chinese Journal of Hydrodynamics, 2012, 27(3): 303–310 (in Chinese) [Google Scholar]
- LI F, HUANG Q, PAN G. Effect of hydrofoil leading edge waviness on hydrodynamic performance and flow noise[J]. Ocean Engineering, 2021, 231: 108883 [Google Scholar]
- WANG Xihui, HUANG Qiaogao, PAN Guang. Numerical research on influence of fairwater shape on flow-induced noise of submarine[J]. Shipbuilding of China, 2020, 61(2): 262–272 (in Chinese) [Google Scholar]
- MOONESUN M, KOROL Y, DALAYELI H. CFD analysis on the bare hull form of submarines for minimizing the resistance[J]. International Journal of Maritime Technology, 2015, 3: 1–16 [Google Scholar]
- JAVADI M, MANSHADI D, KHERADMAND S. Experimental investigation of the effect of bow profiles on resistance of an underwater vehicle in free surface motion[J]. Journal of Marine Science and Application, 2015, 14: 53–60 [Google Scholar]
- HU Chengxing, HUANG Xuhui, LI Hongmei. The location of boundary-layer transition detected by pressure fluctuation measurements[J]. Journal of Experiments in Fluid Mechanics, 2002, 16(2): 67–71 (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 试验模型组成 |
| In the text | |
|
图2 模型艏部线型示意图 |
| In the text | |
|
图3 脉动压力传感器和水听器安装示意图 |
| In the text | |
|
图4 试验流程 |
| In the text | |
|
图5 不同航速下实验测试照片 |
| In the text | |
|
图6 3.08 m/s下3个测量点脉动压力的时间历程 |
| In the text | |
|
图7 3.08 m/s下3个测量点脉动压力的频域曲线 |
| In the text | |
|
图8 不同速度下的脉动压力变化曲线 |
| In the text | |
|
图9 3.08 m/s下不同艏部线型模型脉动压力强度变化曲线 |
| In the text | |
|
图10 不同线型的脉动压力强度峰值点位置 |
| In the text | |
|
图11 线型1噪声和背景噪声测量结果 |
| In the text | |
|
图12 线型1不同速度下的噪声频谱 |
| In the text | |
|
图13 线型2不同速度下的噪声频谱 |
| In the text | |
|
图14 线型3不同速度下的噪声频谱 |
| In the text | |
|
图15 线型4不同速度下的噪声频谱 |
| In the text | |
|
图16 线型5不同速度下的噪声频谱 |
| In the text | |
|
图17 3.08 m/s速度下不同线型的1/3倍频程 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.