| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 152 - 159 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710152 | |
| Published online | 03 April 2019 | |
Real-Time Artifact Compensation for Depth Images of Multi-Frequency ToF
多频飞行时间相机实时深度补偿算法研究
1
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
2
School of Computer Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
Received:
6
March
2018
During the last few years, Time-of-Flight(TOF) sensor achieved a significant impact onto research and industrial fields due to that it can capture depth easily. For dynamic scenes and phase fusion, ToF sensor's working principles can lead to significant artifacts, therefore an efficient method to combine motion compensation and kernel density estimate multi-frequency unwrapping is proposed. Firstly, the raw multi-phase images are captured, then calculate the optical flow between each frequency. Secondly, by generating multiple depth hypotheses, uses a spatial kernel density estimation is used to rank them with wrapped phase images. Finally, the accurate depth from fused phase image is gotten. The algorithm on Kinect V2 is validated and the pixel-wise part is optimized using GPU. The method shows its real time superior performance on real datasets.
摘要
针对多频飞行时间相机在曝光时间内物体运动以及相位融合中产生的偏差,提出一种基于光流以及空间核密度估计的实时补偿算法。首先获取原始的多频相位图像,计算出不同频率之间的相对光流,获得每种频率下的补偿相位;在此基础上针对不同频率的相位做出可信度假设并利用空间核密度估计对其进行排名,获得最终的相位融合图并生成对应的深度图。实验部分,使用Kinect V2相机获取的原始多频相位图对算法进行验证,同时利用GPU进行并行加速;结果表明该算法可以实时对物体平行于光轴运动的相位融合偏差进行补偿,有效地提高了深度图像的精度和稳定性。
Key words: ToF / multi-frequency / optical flow / kernel density estimation / Kinect V2
关键字 : 飞行时间相机 / 多频 / 光流 / 空间核密度估计 / Kinect V2
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
消费级别的飞行时间相机由于不需要复杂的机械安装与校准, 并且可方便的提供物体的深度信息成为学术界和工业界研究的热点[1]。但是由于其测距原理限制, 会产生一些系统和非系统的误差[2]。当物体运动时, 对应的相位图像也会移动, 在利用多帧相位图进行深度融合计算时, 由于数据差异较大, 会造成边缘数据的不一致和不稳定, 严重影响后续使用。从文献[1]中可以明显看出快速运动人体深度图像的边缘缩减问题。
为了解决移动物体单帧中的相位图移动问题, Hussmann等[3]利用相位图差标记出物体移动区域, 然后根据物体线性移动的特点计算出移动距离, 最终利用FPGA进行加速, 可达到实时效果。但是该算法仅限于线性平动的物体。Lindner等[4]在传统四相位漂移算法的基础上, 计算任意连续2个相位之间稠密的光流场并对其他相位图进行补偿。Lefloch[5]在文献[4]的基础上, 只计算一组频率中首尾2帧的光流场, 其余光流场则由线性插值而来, 该算法提高了整体的计算效率, 但是其严重依赖运动的连续性, 当首尾2帧出现周期性运动时会出现较大的系统偏差。Crabb等[6]利用概率框架输入多张同频率相位图对深度图像进行全局优化, 但是无法很好地解决物体运动的问题。
为了增加深度测距的稳定性以及距离, 仿照多普勒雷达效应, 在单一频率的基础上产生了多频飞行时间相机, 利用不同频率在同一位置返回的距离, 采用经典的中国剩余定理[7]可以较大地提升精度并扩大无歧义的距离。但是中国剩余定理仅适用于系统误差与噪声较小的情况。由于相位的测定与物体的距离及表面的反射率有关, 因此可认定物体表面的反射率局部恒定, 在该假设下, 利用马尔科夫随机场、数据项以及反射平滑项作为目标函数进行优化成为一种通用的方法。Droeschel等[8]利用2个不同的时间飞行相机模拟双频的相位图, 采用马尔科夫随机场加入频率和反射率的数据项作为优化目标。Ti等[9]则模拟间隔频率的时间飞行相机相位图生成方式, 只利用一次生成的多频相位图对整体进行优化。Lawin[10]利用空间核密度估计对每种频率的可信度进行对比, 有效地提高了整体测量距离和准确度。
为了提高多频飞行时间相机在物体运动时的测距精度, 本文结合单一频率的运动补偿以及多频率的空间核密度预估相位融合算法(以下简称为MCO算法), 分别利用大范围偏移的光流进行运动补偿及空间核密度对相位进行融合。最终利用Kinect V2相机验证算法的有效性。结果表明, 该算法可以针对物体平行于光轴的运动, 可实时有效地提高深度图像的精度和稳定性。
1 背景
1.1 飞行时间测距原理
传统的单一频率飞行时间相机利用传感器发出经调制的近红外光, 遇物体后反射, 计算光线发射和反射的相位差来计算被拍物体的距离。针对单一频率的测距, 学者们为了简化计算, 利用4张1组的相位图进行计算, 其距离计算如公式(1)~(2)所示:
式中,c为光速, φ为相位差, ω为角速度, Pi(i=0, 1, 2, 3)表示对应时刻的相位图, 其差值为2张图的标量之差, 为对应像素的直接相减。
当一组相位图包含任意N张图时, 其相位计算如公式(3)[11]所示
式中,p0表示相位的补偿, vn表示对应频率下的测量电压。
由以上测距原理可以推出对应调制频率可探测到的无歧义的距离最大距离为
式中,f为信号的频率, f=ω/2π。
1.2 多频飞行时间原理
为了解决单一频率测量距离有限以及稳定性不高的问题, 人们提出了多频率的飞行时间测距方法。利用不同频率在同一位置的返回距离进行融合, 其经典的方法为中国剩余定理, 如等式(5)和(6)所示:
式中,i表示频率, ri表示第i个频率下的无歧义最大距离, mod表示取余, D表示实际的距离。该算法适合在无噪音下的多频率融合。di表示取余后的实际距离, ki表示该频率下可能取到的的整数倍数。
Kinect V2是目前消费级别深度相机中比较常用的一种多频率的飞行时间相机, 该相机在1张深度图像的生产中采集了3种不同频率的相位图(如图 1[10]所示), 每组频率包含3张相位图。
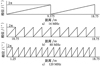 |
图1 Kinect V2在不同频率及相位下的对应距离 |
1.3 光流原理
假设2帧图像间的亮度恒定而且保持空间的一致性, 那么光流可以评估了2帧图像之间的变化光流场的目的是找到连续帧之间每一个像素的运动信息(δx, δy), 假设2帧图像的时间差为δt, 则约束方程可以写为:
本文的目的是求出连续的相位图之间的运动信息, 当连续相位图的运动基本平行于相机光轴时, 此时同一位置的亮度相近, 可认为其满足光流运算的基本假设。
2 算法
如图 2所示, 采用第三方的驱动libfreenect2[13]获取原始的相位图像, 每次获取3种频率各3幅图(在框架图中我们只选取其中的1幅作为代表), 进行整体预处理后进入框架图进行计算。以频率2(16 MHz)为基准, 使用大范围偏移的光流分别对频率1和频率3进行光流计算, 然后对其分别进行补偿。在补偿相位图基础上利用空间核密度对不同频率相位的可信度进行排名, 在此基础上进行相位融合, 利用最终融合的相位图生成深度图。
 |
图2 算法整体框架图 |
2.1 预处理
在进行整体的算法之前, 对相位图进行预处理。为了降低相位图整体的噪声但不影响高频的边界部分, 对每张相位图进行双面滤波。为了加速后续的整体算法, 对运动部分进行粗略检测并进行标记, 我们采用相位图差(灰度图差)的方法, 计算2张相位图的数值差, 如图 3a)所示; 将图 3a)中阈值设定为3后提取二值图像(见图 3b)), 在后面的光流计算中只对标记区域进行运动补偿。
 |
图3 相位图差及对应二值图 |
2.2 大范围偏移光流计算
设定I1和I2为需要处理的2帧连续图像。x:(x, y)则表示图像上的任意点, w:(u, v)表示对应的光流场。在遵守对应点的颜色值一样的假设下, 传统的光流方法一般建立如下3个约束来优化整个问题。
式中,Ψ表示惩罚函数,  用来处理一些外点。该项为颜色一致约束项。
用来处理一些外点。该项为颜色一致约束项。
考虑到光照的影响, 因此加入(9)式的约束, 表示在颜色梯度上的一致性:
为此加入整个计算空间的平滑项保证整体计, 结果的平滑减少二义性
以上的三项所组成的光流模型可以处理移动较小的结果。经过实验发现, 在高速运动中相同频率相邻相位图之间将会出现多达10个像素的偏移, 所以需要大范围偏移的光流方法并且针对平滑项进行修改。受到文献[10]的启发, 在上面的3项外, 本章加入最近邻的加权平均项(见公式(11))保证在局部运动范围内有着较好的平滑度。
该项表示J个最近邻区域匹配的插值的加权平均, ρj(x)是其中的权重, 当无相应匹配为0, 有对应匹配是其对应距离。在本章中选取J=5。
以上4项加起来为非凸函数, 因此无法显式地求出最优解。为了提高算法的速度, 需要尽可能采用比较接近结果的初始值, 因此采用特征算子匹配对2帧图片项进行初始匹配, 可以将其解作为初始值带入整个目标函数中。因此加入第五项Edesc(w1), 既可以作为约束项, 也可以作为整个模型的初始解。
最终光流的目标函数为公式(13), 初始化时, 采用HOG算子算出每张图的特征算子并对其进行匹配, 在此基础上将其转化为稀疏光流场。将其作为初始解带入整个能量模型中, 利用逐次超松弛(SOR)迭代进行计算直到整个能量模型收敛。
在本文中, 选取β1=5, β2=5, β3=25。
图 4为通过公式(13)计算得出的连续2帧相位图及其对应的可视化光流。
 |
图4 连续2帧相位图及其对应的光流图 |
2.3 基于空间核密度估计的相位融合
在相位融合中, 为了提高相位融合的精度和整体的测量距离, 受到文献[10, 15]的启发, 对每种频率补偿后的相位图分别做出可信度假设并利用空间核密度估计对其进行排名, 最终获得精确稳定的融合相位。
针对每一个像素x的可信度假设p(ti(x)), 利用空间核密度的计算如下:
式中,j表示不同的假设数, 在本文中使用双假设; N(x)表示其邻域像素, 其定义为半径r内的所有像素, r在本文中设定为3;K是内核函数, 本文采用高斯内核, 其中K(x)=e-x2/2h2, h=r/2为内核尺度。
ωjk是相邻像素的对应权重, 如(15)式所示, 主要包含3部分:①G(x-xk, σ)利用高斯函数表示空间权重; ②p(tj(xk)|nj(xk))表示的多频解算的概率, 其中nj=(n1, n2, n3)分别表示解算向量的系数; ③p(tj(xk)|aj(xk))表示相位的概率, 其中aj=(a1, a2, a3)分别表示3种对应频率下的振幅。
整体平滑 经过如上计算之后, 可以获取一张比较准确的相位图。在此基础上, 针对空间中的每一个像素点与其周围N个点的关系, 提出保持边缘Laplacian平滑的能量函数:
式中,P(x)表示当前的相位值。
在本章中, σlap=0.01, 与可信度假设类似, 取半径r=3以内的所有像素点作为其邻域点计算边缘的有效性。此后对(16)式进行优化, 获得最终的相位图。最后对相位图进行处理, 获取对应的深度图像。
3 实验验证
为了验证算法的有效性, 我们分别使用公有数据集以及自主采集的数据对算法进行验证。其中自主数据利用Kinect V2采集了多组不同环境中运动的原始相位数据, 所有图像大小均为512×424。
3.1 数据集验证
采用论文[10]中提供的数据集作为空间核密度估计算法的验证部分, 其中主要验证静态状态下文献[10]中的算法(下称Lawin算法)与本文MCO算法的对比。
其中图 5为某教堂的部分, 图 5a)为数据集提供的标准深度图像, 图 5d)为在固定角度下的彩色图像。图 5b)为Lawin算法计算出来的结果, 图 5c)为MCO算法计算出来的结果。图 5e)和5f)则分别为Lawin和MCO算法与标准深度图像的误差图。按照公式(18)对误差比例进行量化, 其中MCO算法的误差比例为15.87%, Lawin算法的则为22.14%。本文还利用公式(19)对误差的具体数值进行统计, 其中Lawin算法的整体平均误差为1 998 mm,MCO算法的整体平均误差为1 640 mm。
与图 5的图例相同, 图 6为某图书馆的一角。分别利用公式(18)和(19)对误差进行量化后, Lawin算法的误差比例Ep为24.54%, MCO算法的误差比例为18.67%, Lawin算法的整体平均误差Ed为2 037 mm, 本文算法为1 720 mm。
式中,N表示像素点的个数, gi表示该点的真正距离, ci表示计算出来的该点的距离。
 |
图5 某教堂的数据对比(图中所有单位为mm) |
 |
图6 某图书馆的数据对比(图中所有单位为mm) |
3.2 实际数据验证
利用Kinect V2采集了一些实际的运动数据对整体算法进行对比验证。
图 7和8分别为高速挥手和挥动箱子下的深度图对比, 并分别与libCRT算法进行比对。从结果图中可以看出, libCRT算法会不同程度地减小运动部分的面积, 主要是因为运动造成了连续的相位图的边缘差比较大, 当采用中国剩余定理计算出的不同频率下的融合相位差距比较大时, 系统会自动按照算法取周围的平均或者取0, 这样会使得边缘数据产生较大的问题。本文算法则将所有的相位数据利用光流转化到同样频率下, 这样就会减少融合时的误差, 尤其减少了运动时边缘的数据的差距, 提高了边缘数据的稳定性; 而后利用空间核密度估计有效地提高了整体的精确性。
 |
图7 挥动手臂时对比(图中所有单位为mm) |
 |
图8 挥动箱子时对比(图中所有单位为mm) |
3.3 运算环境与时间
本文实验环境为Visual studio 2015, CPU为Intel Core i5处理器, 主频为2.2 GHz, 显卡为Intel HD Graphics 5500, 内存为8 GB。整体的算法主要利用C++实现, 因为空间核密度估计部分是局部进行的, 因此可以进行并行计算, 在实验中, 我们使用GPU进行加速。经过测算, 1幅图的耗时如表 1所示, 可以看出光流计算是最耗时的部分, 但是由于我们只计算运动部分的光流, 极大减小了运算量, 算法的时效性得以保证, 可达到每秒10帧, 满足实时应用的要求。
耗时测算
4 结论
本文针对飞行时间相机在产生的系统以及运动产生的偏差, 提出一种基于光流和空间核密度估计相结合实时补偿算法。首先获取原始的多频相位图像, 计算出不同的频率之间的相对光流, 获得每种频率下的补偿相位; 在此基础上针对不同频率做出可信度假设并利用空间核密度估计对其进行排名, 获得最终的相位融合图并生成对应的深度图。在实验阶段利用Kinect V2相机算法进行验证并利用GPU对空间核密度的相位融合部分进行优化, 实验结果表明, 与libCRT算法和Lawin算法相比, 本文算法在取得了较好的实验效果并可以达到实时效果。
本文算法适合处理大范围偏移下的物体运动补偿。在下一步的应用中, 期望可以处理相机运动所造成的补偿, 并加入更多的传感器信息, 如IMU的信息或者彩色图像的信息, 建立一个由粗到精细的框架, 利用IMU或者彩色图像进行粗略的补偿处理, 减少光流的计算, 提高算法的整体效率。
References
- Zuo X, Wang S, Zheng J, et al. High-Speed Depth Stream Generation from a Hybrid Camera[C]//ACM on Multimedia Conference, 2016: 878-887 [Google Scholar]
- Lindner M, Kolb A. Lateral and Depth Calibration of PMD-Distance Sensors[C]//International Symposium on Visual Computing, 2006: 524-533 [Google Scholar]
- Hussmann S, Hermanski A, Edeler T. Real-Time Motion Artifact Suppression in TOF Camera Systems[J]. IEEE Trans on Instrumentation & Measurement, 2011, 60(5): 1682-1690 [Article] [CrossRef] [Google Scholar]
- Lindner M, Kolb A. Compensation of Motion Artifacts for Time-of-Flight Cameras[C]//Dagm 2009 Workshop on Dynamic 3D Imaging, Springer-Verlag, 2009: 16-27 [Google Scholar]
- Lefloch D, Hoegg T, Kolb A. Real-Time Motion Artifacts Compensation of ToF Sensors Data on GPU[C]// Three Dimensional Imaging, Visualization, and Distday International Society for Optics and Photonics, 2013: 87380U-87380U [Google Scholar]
- Crabb R, Manduchi R. Probabilistic Phase Unwrapping for Single-Frequency Time-of-Flight Range Cameras[C]//International Conference on 3D Vision, 2014: 577-584 [Google Scholar]
- Jongenelen A P P, Bailey D G, Payne A D, et al. Analysis of Errors in ToF Range Imaging with Dual-Frequency Modulation[J]. IEEE Trans on Instrumentation & Measurement, 2011, 60(5): 1861-1868 [Article] [CrossRef] [Google Scholar]
- Droeschel D, Holz D, Behnke S. Multi-Frequency Phase Unwrapping for Time-of-Flight Cameras[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, 2010: 1463-1469 [Google Scholar]
- Ti C, Yang R, Davis J. Single-Shot Time-of-Flight Phase Unwrapping Using Two Modulation Frequencies[C]//International Conference on 3D Vision, 2016: 667-675 [Google Scholar]
- Lawin F J, ForsSÉn P E, OvrÉN H. Efficient Multi-Frequency Phase Unwrapping Using Kernel Density Estimation[C]//European Conference on Computer Vision, Springes, 2016: 170-185 [Google Scholar]
- JÄhne B. Theoretical and Experimental Error Analysis of Continuous-Wave Time-of-Flight Range Cameras[J]. Optical Engineering, 2009, 48(1): 3602 [Article] [Google Scholar]
- Lucas B D, Kanade T. An Iterative Image Registration Technique with an Application to Stereo Vision(DARPA)[J]. Nutrient Cycling in Agroecosystems, 1981, 83(1): 13-26 [Article] [Google Scholar]
- Xiang L, Echtler F. libfreenect2: Release 0.2[EB/OL]. (2016-04-28)[2018-02-22]. http://github.com/OpenKinect/libfreenect2 [Google Scholar]
- Brox T, Malik J. Large Displacement Optical Flow:Descriptor Matching in Variational Motion Estimation[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2011, 33(3): 500-13 [Article] [Google Scholar]
- Felsberg M, Forssen P E, Scharr H. Efficient Robust Smoothing of Low-Level Signal Features[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2009, 28(2): 209-22 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 Kinect V2在不同频率及相位下的对应距离 |
| In the text | |
 |
图2 算法整体框架图 |
| In the text | |
 |
图3 相位图差及对应二值图 |
| In the text | |
 |
图4 连续2帧相位图及其对应的光流图 |
| In the text | |
 |
图5 某教堂的数据对比(图中所有单位为mm) |
| In the text | |
 |
图6 某图书馆的数据对比(图中所有单位为mm) |
| In the text | |
 |
图7 挥动手臂时对比(图中所有单位为mm) |
| In the text | |
 |
图8 挥动箱子时对比(图中所有单位为mm) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


