| Issue |
JNWPU
Volume 37, Number 2, April 2019
|
|
|---|---|---|
| Page(s) | 330 - 336 | |
| DOI | https://doi.org/10.1051/jnwpu/20193720330 | |
| Published online | 05 August 2019 | |
Research on Multi-Sensor Resource Dynamic Allocation Auction Algorithm
多传感器资源动态分配拍卖算法研究
1
School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China
2
Systems Engineering Research Institute, China State Shipbuilding Corporation, Beijing 100094, China
3
China National Aeronautical Radio Electronics Research Institute, Shanghai 200233, China
Received:
16
April
2018
This paper designs a multi-sensor resource dynamic allocation method based on auction algorithm. Tasks are prioritized according to the needs of the engineering field. Task priority is used as the basis for multi-sensor resource allocation order, taking into account the target's threat value and information needs. The sensor and task pairing function is established and used to measure the sensor resource dynamic allocation, we also use Analytic Hierarchy Process to determine the weight of each performance parameter in the pairing function (such as detection probability, intercept probability, positioning accuracy, tracking accuracy, recognition probability, etc.). The auction algorithm is improved by adding resource dynamic allocation constraints, which not only ensures the continuous execution of the target task, but also improves the dynamic allocation efficiency of multi-sensor resources. The simulation results show that the allocation method in this paper is scientific and reasonable.
摘要
设计了一种基于拍卖算法的多传感器资源动态分配方法。根据工程领域需求对任务进行优先级排序,作为多传感器资源分配顺序的依据,考虑了目标的威胁值和信息需求等因素。建立传感器与任务配对函数,将配对函数作为传感器资源动态分配的衡量指标,并使用层次分析法确定配对函数中各性能参数(如检测概率、截获概率、定位精度、跟踪精度、识别概率等)的权值。通过加入资源动态分配约束改进拍卖算法,保证目标任务连续性执行,提高了多传感器资源动态分配效能。通过仿真验证得出该分配方法科学合理有效。
Key words: auction algorithm / pairing function / multi-sensor management
关键字 : 拍卖算法 / 配对函数 / 多传感管理
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来国内外学者提出了多种传感器资源分配算法。文献[1]构建了在效能函数基础下的传感器管理的最优决策模型, 求得量测前与量测后的目标信息增量, 将其作为性能指标, 并以此进行分析总结得到将预测误差协方差作为效能函数对传感器资源进行分配时能够达到最优的效果。文献[2]采用序贯卡尔曼滤波算法, 将自适应协方差与配对函数相结合, 从而使得配对系数能够自动更新, 使得分配过程更加有效。文献[3]则是采用神经网络自主学习的能力和模糊控制克服了目标参数量化以及优先级排序时的困难, 使得这种资源分配方法比传统的方法更加高效。文献[4]提出一种考虑传感器对目标的匹配精度、传感器作用范围和协同能力的目标函数, 建立一种基于改进蚁群算法的海上编队传感器资源分配模型, 提高了算法的收敛速度与时间满意度。
从以往的研究文献来看, 在使用效能函数作为传感器资源分配依据的数学模型中, 大多学者对于效能函数中传感器与目标的配对函数没有进行具体设定, 未给出建立配对函数所需考虑的因素和各因素对应的权重系数。且大多对传感器的资源分配为静态过程, 即预先设定任务列表、平台和传感器的参数, 且只考虑某一个时刻的传感器资源分配, 但在真实战场环境中, 由于平台参数和传感器性能参数随战场态势实时变化, 任务列表实时更新, 需要定期对传感器资源进行分配, 因此, 对传感器资源的分配为动态过程。本文通过资源动态分配约束, 各传感器进行协商交换任务, 在保证分配效能的前提下, 保证任务的连续性, 即每个目标的所有任务由某个平台(或某几个平台)连续执行, 以此来减少目标交接时的损耗。本文主要研究多传感器资源动态分配拍卖算法, 根据工程领域需求对任务进行优先级排序, 并使用层次分析法建立配对函数, 再通过改进拍卖算法在能力约束和动态资源约束的条件下对传感器资源进行动态分配。
1 多传感器资源动态分配模型
1.1 任务优先级
任务优先级的排序分为2步, 同类任务和非同类任务。
根据战场的作战需求, 非同类任务的执行具有先后顺序, 攻击类任务优先级最高, 依次为目标交接类, 最后为信息需求类(识别、跟踪、搜索)。
故非同类任务的优先级排序如图 1所示:
同类任务中, 优先级分别定义为:
攻击类, 首先满足目标照射(制导)需求, 其次按照攻击顺序进行优先级排序;
目标交接类, 首先满足对友机的目标交接, 其次按照威胁排序、时间限制进行;
信息需求类, 按照以下规则排序:
1) 高威胁、高信息需求的敌方目标排在最前;
2) 低威胁、高信息需求的目标排在其次;
3) 确认为敌方目标和状态不明的目标;
4) 我方及友方目标排在最后。
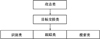 |
图1 非同类优先级排序 |
1.2 传感器-任务配对函数
不同的传感器对不同的任务目标具有不同的能力, 在传感器管理中, 一般使用传感器(传感器组)-任务配对函数来表示不同传感器对不同任务目标的执行能力。配对函数值越大, 则该传感器(或组合)执行该任务目标的效果越好(即更适于执行该任务)。定义qij()为传感器(或组合)i对任务j的配对函数。
根据任务目标不同配对函数也不同, 函数中包含的因素有:目标检测概率(TDP)、截获概率(IP)、目标定位精度(TPA)、跟踪精度(TA)、跟踪稳定性(TS)、识别准确性(TR)、识别速度(IS)、目标击毁概率(TEP)。
不同的传感器与不同的任务目标配对会得到不同的qij()值, 其中加权系数的选取要视不同目标任务活动的情况而定, 根据各个性能参数对不同的任务影响, 使用层次分析法[5], 确定各个性能参数在配对函数中的权值。
分别构造搜索任务、识别任务、定位任务、跟踪任务、攻击任务的成对比较矩阵As, Ar, Al, AT, Af。搜索任务主要考虑检测概率、截获概率; 识别任务主要考虑识别准确性、识别速度; 定位任务主要考虑目标定位精度; 跟踪任务主要考虑定位精度、跟踪精度、跟踪稳定性; 攻击任务主要考虑目标定位精度、跟踪精度、目标击毁概率。使用层次分析法中九标度法分别对各因素进行两两比较, 不同类型任务中主要考虑的因素重要性高于其他因素。
经过计算, 成对比较矩阵As, Ar, Al, AT, Af通过了一致性检验, 据此计算得出相应的特征向量(权向量), 特征向量中对应各因素的值即为各个性能参数在配对函数中的权值。以此得到搜索任务qijS ()、识别任务qijR ()、定位任务qijL ()、跟踪任务qijT ()、攻击任务qijF ()的配对函数分别为:
1.3 代价函数
代价函数一般描述为任务对系统资源的消耗, 通常考虑传感器资源代价, 时间代价等因素, 故定义代价函数为
α, β为权重系数, α+β=1, 可根据两因素(资源代价和时间代价)对代价函数的影响大小(或重要性)设定α、β的值, 在此文的仿真中, 设定权重系数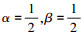 。其中
。其中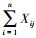 为在执行任务j时使用传感器数目的总和, Xmaxnum为执行某类型任务可用的最大传感器数量。Ct()为时间代价[6], Ct()=1-ai, ai为性能值, a为正常执行某类型任务所需的时间, b为执行某类型任务所需的最长时间。当执行任务的时间在时间门限a内, 性能值为1, 超过时间门限a时, 完成任务耗费的时间越长, 性能越低, 则代价越大。性能随时间衰减如图 2所示:
为在执行任务j时使用传感器数目的总和, Xmaxnum为执行某类型任务可用的最大传感器数量。Ct()为时间代价[6], Ct()=1-ai, ai为性能值, a为正常执行某类型任务所需的时间, b为执行某类型任务所需的最长时间。当执行任务的时间在时间门限a内, 性能值为1, 超过时间门限a时, 完成任务耗费的时间越长, 性能越低, 则代价越大。性能随时间衰减如图 2所示:
图 2中, t表示从开始任务分配到完成该任务的时间; a, b表示与任务有关的时间门限。
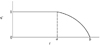 |
图2 时间代价曲线 |
1.4 能力约束
一个传感器(组)可分配给多个任务, 任务个数受传感器(组)能力ti约束, 它表示传感器(组)一次可执行的任务个数, 传感器组合的能力由组合中具有最小能力的传感器决定。一个任务可被多个传感器执行, 但至少有一个传感器。因此, 多传感器资源分配模型应满足以下约束条件[7]。
传感器最大能力约束
传感器的任务约束
式中,n表示任务的个数, m表示传感器(组)的数量, xij表示使用传感器(组)i执行任务j。(8)式保证传感器执行的任务数不超出其能力范围, (9)式保证每个任务都有传感器执行。
1.5 资源动态分配约束
在整个敌我双方的作战过程中, 根据战场态势和作战任务的变化需对传感器资源进行多次分配, 而在每次分配中, 传感器管理系统更倾向于将传感器分配给执行某项任务能力最强的传感器, 而该传感器由于在前几个阶段未执行与该目标相关的任务, 因此没有该目标的距离、速度、位置等信息, 因此该传感器所在的平台需对目标进行重新探测或与其他平台完成目标交接来获取信息, 则需耗费更多的资源和时间。因此为了保证任务的连续性, 减少损耗, 在每轮次完成竞拍后, 各传感器之间进行协商, 交换任务。设定Si为执行目标target x的第n-1个任务task n-1的传感器。在新一轮次的传感器资源分配中, Sj被分配给目标target x执行第n个任务taskn, 任务task n与Sj的配对函数为qj, nS(), 任务task n与Si的配对函数为qi, nS()。若Si与Sj不是同一平台的传感器, 则需比较qi, nS()与qj, nS()的大小, 若qj, nS()-qi, nS()小于某一阈值qmin, 则继续由传感器Si执行任务task n, 并检测传感器Si执行的任务数是否超过能力约束。若qj, nS()-qi, nS()大于某一阈值qmin, 则Si所在的平台与Sj所在的平台完成目标交接和信息共享, 然后由传感器Sj执行任务task n。
1.6 动态分配数学模型
根据上述分析, 多传感器动态资源分配模型为:
式中,第1, 2个方程是为了保证传感器资源分配的高效性, 第3, 4个方程进行能力约束, 第5, 6方程进行资源动态分配约束, 保证任务的连续性。
2 多传感器资源动态分配拍卖算法
根据已建立的多传感器资源动态分配模型, 采用拍卖算法对任务进行分配。多传感器管理系统首先确定各任务的竞拍顺序, 发布一次竞拍中要处理的任务列表, 并宣布拍卖开始。各任务根据配对函数计算与各传感器(组)的配对函数值。待轮到某个任务竞拍时, 该任务从所有传感器(组)中选择最优的组, 即该传感器(组)资源分配给该任务。具体实施步骤如下:
步骤1 统计并发布当前任务列表。
步骤2 按照任务优先级进行排序, 按照顺序逐一进行拍卖。
步骤3 针对第一个任务, 对所有可能执行任务的传感器根据配对函数值进行比较, 得出最佳的传感器组Mi。
步骤4 根据传感器的能力建立禁忌列表, 即一个传感器所分配的任务达到上限时, 认为该传感器处于禁忌状态而不参与其他任务的竞拍。
步骤5 依次进行余下任务的拍卖, 拍卖一个任务, 将该任务分配给拍卖的传感器(组), 并将该已经达到能力上限的传感器增加到禁忌列表中, 依次拍完所有目标。
步骤6 传感器组间进行协商, 根据上一次任务分配结果, 执行同类任务的传感器之间根据任务的连续性进行任务交换, 在保证分配效能较高的情况下, 尽量使一个目标的所有任务由一个平台连续执行。
步骤7 时间允许, 进入下一轮拍卖, 将所有任务随机排序, 回到步骤3;如果有新任务出现重新回到步骤1。
步骤8 拍卖限制时间到, 取出最优的方案与次优方案, 若最优方案的配对函数值与次优方案的配对函数值大于等于阈值, 则输出最优方案, 若小于阈值, 则比较两方案的代价函数值, 输出代价函数值更小的方案。根据输出方案进行传感器的分配。
3 仿真分析
设定我方有8架飞机, 每架飞机为一个传感器平台, 每个平台携带3种不同类型的传感器[9]。敌方有10架飞机, 我方飞机需对敌方目标依次完成“远距探测任务”、“中远距探测任务”、“中远距识别任务”、“中距探测任务”、“中距识别任务”、“中近距探测任务”、“定位任务”、“跟踪任务”、“中近距识别任务”、“攻击任务”。
图 3为未使用资源动态分配约束时, 使用拍卖算法对多传感器动态资源分配结果。图 4为在资源动态分配约束下改进拍卖算法对多传感器动态资源分配结果; 当前时刻表示触发(或执行)该任务的时间点; 敌机序号表示该任务是针对哪架敌机执行; 任务的优先级表示, 在同一当前时刻下, 该任务的优先级, 优先级的数值越小, 任务优先级越大, 即当任务的优先级为1时, 该任务的优先级最大; 任务类型表示执行某个阶段(远距、中远距、中距、中近距、近距)某种类型(探测、识别、定位、跟踪、攻击)的任务; 执行该任务的平台表示将该任务分配给该平台的传感器执行。
本文以4号敌机为例, 探讨多传感器资源动态分配结果。如图 3所示, 4号敌机的任务分别由平台7, 6, 8, 2, 4完成。在中远距阶段, 平台7需要把探测信息共享给平台4, 由平台4完成中远距识别任务; 在中距阶段平台4需将目标交接给平台6, 由平台6完成中距识别任务; 在中近距阶段, 平台7需要将目标交接给平台8, 由平台8继续执行探测任务, 并将信息共享给平台6, 平台6再与其他平台合作完成攻击任务。在对4号敌机的作战过程中, 需要多次进行目标交接和信息共享, 大大降低了传感器的工作效率, 消耗时间。如图 4所示, 通过加入资源动态分配约束, 由平台7完成远距、中远距、中距、中近距任务, 然后由平台7与平台3, 4分别协同完成定位任务和跟踪任务, 最后由平台3, 4完成最后的识别任务和攻击任务。由图 3~4可知, 加入资源动态分配约束的改进拍卖算法对传感器资源分配更加科学合理。
为进一步展现拍卖算法与改进拍卖算法的区别, 分别列出表 1和表 2拍卖算法改进前后(即是否加入资源动态分配约束)每个目标敌机所有任务阶段累计配对函数值与代价函数值, 其中效能函数值为配对函数与代价函数的差值[10]。
从表 1和表 2中可知, 加入资源动态分配约束后, 配对函数值和代价函数值均降低。为了保证任务的连续性, 更倾向于采用原有平台执行任务, 但原有平台与该任务的配对函数值低于新分配给该任务的平台配对函数值, 所以导致配对函数值下降。但由于无需花费时间进行信息共享和目标交接, 因此代价函数值降低。改进后的效能值略大于改进前的效能值, 证明改进后的动态分配拍卖算法更有效。
图 5展现了各累计函数值随着任务阶段的变换。初始任务阶段的任务为远距、中远距探测任务, 由于目标任务较单一, 且战场态势变化较小, 因此任务由一个平台连续执行或更换其他更优的平台执行对传感器资源分配效能影响较小, 因此改进前后函数值重合。在中距、近距等任务阶段, 由于战场态势变化大, 因此不同平台对不同任务的执行能力变化较大且差异明显, 因此对某一目标执行任务的平台可能会根据战场的态势和平台的能力而更换, 由于在复杂的作战环境下, 更换执行目标任务的平台会花费更多的时间, 因此时间代价大大增加, 而若为了保证任务的连续性不更换平台, 则该平台并不是当前战场状态最适合执行该任务的平台, 配对函数值减少。因此改进前后的累计函数值差别较大。从图 5中可知, 虽改进后配对函数值降低, 但代价函数值降低幅度大于配对函数值, 因此效能函数值高于改进前, 所以加入资源动态分配约束的改进拍卖算法提高了传感器资源分配效能。
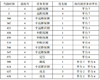 |
图3 多传感器资源动态分配拍卖算法结果图 |
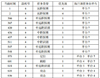 |
图4 多传感器资源动态分配改进拍卖算法结果图 |
改进前目标的函数值(无资源动态分配约束)
改进后目标的函数值(有资源动态分配约束)
 |
图5 累计函数值与任务阶段结果图 |
4 结论
本文设计了一种基于拍卖算法的多传感器动态资源分配方法。根据目标的威胁值和信息需求等因素对目标进行优先级排序。在考虑传感器的检测概率、截获概率、定位精度、跟踪精度、识别概率等性能参数下建立传感器与任务配对函数, 并使用层次分析法确定各性能参数的权值。以配对函数作为传感器动态资源分配的衡量指标, 通过加入资源动态分配约束改进拍卖算法, 在保证目标任务连续性执行的前提下, 提高了多传感器资源动态分配效能, 通过仿真验证得出改进后资源分配效能优于改进前的拍卖算法。
References
- Wang Feng, Pan Quan, Wang Yinhuai, et al. An Optimal Decision Model for Sensor Management Based on Efficiency Function Systems Engineering and Electronics, 2007, 29(9): 1472–1475 (in Chinese) [Article] [Google Scholar]
- Yang Tao, Xu Yunshan, Xiao Bingsong, et al. Adaptive Sensor Tracking Resource Allocation Based on Performance Function Electro-Optical and Control, 2014, 21(8): 63–67 (in Chinese) [Article] [Google Scholar]
- Zheng Yujun, Tian Kangsheng, Zhang Jinlin, et al. Adaptive Multi-Sensor Resource Management Method Based on Performance Function Computer Simulation, 2017, 34(5): 322–326 (in Chinese) [Article] [Google Scholar]
- Zhu Weixiao, Zhu Qianwang, Chen Kang. Reseource Allocation Model for Maritime Formation Sensors Based on Improved Ant Colony Algorithm Compute and Modernization, 201412): 15–18 (in Chinese) [Article] [Google Scholar]
- Deng Xue, Li Jiaming, Zeng Haojian, et al. Analysis and Application of Weights Calculation Method of Analytic Hierarchy Process Mathematics in Practice and Theory, 2012, 42(7): 93–100 (in Chinese) [Article] [Google Scholar]
- Wu Wei. Sensor Management Algorithm Based on Bilateral Combination Auction Systems Engineering and Electronics, 2014, 36(10): 1960–1965 (in Chinese) [Article] [Google Scholar]
- Zhang Yue. Design of Multi-Sensor Intelligent Scheduling Scheme Light Industry Machinery, 2017, 35(5): 43–47 (in Chinese) [Article] [NASA ADS] [Google Scholar]
- Yan T, Han C. Sensor Management for Multi-Target Detection and Tracking Based on PCRLB[C]//International Conference on Information Fusion, 2017: 1–6 [Google Scholar]
- Guan Bin Zhou Yijun. Research on Sensor Management Technology of Sea Battlefield Ship Electronic Engineering, 2016, 36(8): 64–67 (in Chinese) [Article] [Google Scholar]
- Tang S, Bi D, Xu Y, et al. Dynamic Sensor Management Algorithm Based on Improved Efficacy Function[C]//IEEE International Conference on Electronic Measurement & Instruments, 2016: 1438–1442 [Article] [Google Scholar]
All Tables
All Figures
 |
图1 非同类优先级排序 |
| In the text | |
 |
图2 时间代价曲线 |
| In the text | |
 |
图3 多传感器资源动态分配拍卖算法结果图 |
| In the text | |
 |
图4 多传感器资源动态分配改进拍卖算法结果图 |
| In the text | |
 |
图5 累计函数值与任务阶段结果图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


