| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 1036 - 1043 | |
| DOI | https://doi.org/10.1051/jnwpu/20193751036 | |
| Published online | 14 January 2020 | |
The Reflection Coefficients Measurement Method for the Underwater Acoustic Materials Based on the Single Vector Hydrophone
单矢量水听器水声材料声反射系数自由场大样测量方法
1
Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China
2
Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China
3
College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
Received:
2
September
2018
In order to obtain the normal acoustic reflection coefficients of underwater acoustic materials in the free field with the wideband pulse signal, a new measuring method with a single vector hydrophone and the post-processing inverse filtering is put forward. Numerical simulations had been conducted to comparatively analyze the measurement performances of the measuring method. The simulation results show that the present method should be established on the high ratio of signal to the noise and it is not sensitive to the system error. The experiment result shows that the post-processing inverse filtering measuring method is more effective comparing with the method without the post-processing inverse filtering, especially the measurement consequence of the post-processing inverse filtering measurement method tends to the theoretical value when the frequency is higher than 2.5 kHz, because limitation of the transducer.
摘要
为了实现水声材料法向声反射系数的自由场宽带测量,将单矢量水听器作为测量系统的核心设备,结合脉冲声发射技术与后置逆滤波信号处理技术,提出了基于单矢量水听器的水声材料法向声反射系数自由场宽带测量方法,通过矢量水听器电子旋转技术实现直达声与反射声的有效分离。讨论了测量系统误差以及接收信号的信噪比等因素对测量结果的影响,该方法对信噪比有一定要求,但对测量系统误差不敏感。实验测试结果表明:与未经后置逆滤波处理的实验测试结果相比,文中所述方法显著提高了测量性能,但受发射换能器低频发射能力限制,实验结果在2.5 kHz以上与理论值吻合较好。
Key words: single vector hydrophone / post-processing inverse filtering / wide band pulse signal / acoustic reflection coefficients
关键字 : 矢量水听器 / 后置逆滤波 / 宽带脉冲 / 声反射系数
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
声反射系数是表征水声材料声学性能的重要参数。目前, 水声材料声反射系数测量方法大致可分为小样实验室声管法和大样自由场测量方法。大样自由场测量一般在大型消声水池中进行, 通过在水池边界敷设消声材料吸收水池边界反射声, 使水听器接收到的信号只有直达声与试样反射声。但由于消声水池消声下限的限制, 低频段多途效应明显; 另外, 自由场测量方法大都会受到试样边缘衍射效应的干扰, 这种干扰在低频段尤为严重。
为了解决上述问题, 脉冲声测试技术广泛应用于水声材料声学参数测量中。发射波形可控、无失真的脉冲声信号是其关键技术。但发射换能器传递函数限制了脉冲声测试技术在有限测量空间中应用的下限频率[1-1]。为此, 人们提出了多种补偿方法, 如李水等提出的宽带脉冲叠加法[3]。该方法采用逆滤波技术, 通过对发射换能器激励信号进行预处理, 补偿发射换能器传递函数, 使发射换能器辐射的信号是理想的尖脉冲, 有效降低了测量的下限频率。与上述方法不同, “后置逆滤波技术”是在水听器接收端对信号进行处理, 达到补偿发射换能器频响的目的。代阳等[4]在声管中采用“后置逆滤波技术”, 实现了水声材料吸声系数的宽带测量。该方法首先获得测量系统的传递函数, 再对观测信号进行补偿, 最后通过将补偿后的观测信号幅度谱与标准试样反射信号幅度谱相除获取试样的声反射系数, 进一步计算得到了吸声系数。
近年来, 矢量传感器已经成功应用于空气声学材料声学参数测量领域[5-5], 如表面阻抗法、声强法等。矢量水听器可同步、共点地拾取声场信息, 扩展了后置信号处理空间, 并且声压、振速信号联合处理即可构成一定的空间指向性[8], 可对试样边缘衍射声等干扰起到一定的抑制作用, 而不必使用常规的大型声压接收阵, 降低了测量系统的复杂度。同时, 矢量水听器声压、振速联合处理的输出主极大方向可通过电子旋转技术指向预定方向, 便于直达声、反射声的有效剥离。此外, 矢量水听器还具有低频指向性好、抗各向同性噪声等优点[9]。因此, 相对于传统的声压水听器, 用矢量水听器测试材料声反射系数具有一定优势。
本文提出了一种水声材料法向声反射系数自由场大样宽带测量方法。本方法将单矢量水听器作为测量系统的核心设备, 结合脉冲声发射技术与后置逆滤波技术, 抑制信号波形失真, 在时域上剔除试样边缘衍射声和多途干扰声, 再通过矢量水听器电子旋转技术实现直达声与反射声的有效分离, 最后通过二者相除获取试样的法向声反射系数。
1 测量过程
为了说明本方法的测量原理, 在阐述测量过程的同时, 给出相关公式推导与仿真结果。
1.1 测量系统传递函数辨识与逆滤波器设计
在对试样进行测试之前, 应首先获得测量系统的传递函数。与传统的声压水听器不同, 矢量水听器包含声压通道与振速通道, 因此需同时获取矢量水听器各个测量通道的传递函数。测量时, 理想的脉冲信号通过发射换能器辐射到水介质中, 再经水声信道传输到接收点, 最后通过矢量水听器接收进而由采集器采集。因此测量系统可划分为三部分, 即信号发射系统、水声信道和信号接收系统。以声压通道为例, 其接收信号模型如图 1所示。
图 1中s(f)为发射信号频谱, T(f)、Hp(f)和R(f)分别为发射系统、声压水声信道和信号接收系统的传递函数, N(f)为背景噪声频谱, Y(f)为测量系统输出信号频谱。后置逆滤波技术就是在测量系统传递函数已知的情况下, 设计逆滤波器对T(f)和R(f)进行补偿。以声压通道为例, 阐述测量系统传递函数辨识的基本原理。
方法1 将信号发射系统与信号接收系统看作一个整体, 即H(f)=T(f)+R(f)。输入信号为x(t), 系统输出信号为y(t), 背景噪声为n(t), 有
式中, X(f), Y(f)和N(f)分别为系统输入信号x(t)、系统输出信号y(t)和背景噪声n(t)的傅里叶变换。经计算, 得到H(f)的估计值为[10]
式中, Gxy(f)为系统输入信号与输出信号的互功率谱, Gxx(f)为系统输入信号的自功率谱。
除上述测量系统辨识方法外, 还可以采用伪随机序列辨识技术[11]。
方法2 设测量系统输入信号x(t)为伪随机序列(MLS序列), 系统输出信号为y(t), 显然有
式中, *表示卷积, h(t)为系统单位冲激响应函数。计算系统输入信号与输出信号的相关函数, 有
式中, rxy为系统输入输出的互相关函数, rxx为输入信号的自相关函数。由于MLS序列具有较好的自相关特性, 即
式中, L=2m-1为序列长度, m为伪随机序列的阶数。易见系统单位冲激响应函数估计值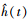 为
为
进一步傅里叶变换即可获得测量系统系统传递函数估计值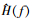 。
。
在获取了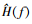 之后, 在频域上设计逆滤波器H-1(f)为
之后, 在频域上设计逆滤波器H-1(f)为
式中, q为正常数, 一般取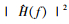 最大值的1%[12]。
最大值的1%[12]。
仿真条件1 发射换能器与水听器等深布放于消声水池中, 二者之间距离为1 m, 发射信号为16阶MLS序列, 分别采用方法1与方法2辨识系统, 信噪比为10, 20和30 dB。考核不同信噪比时2种方法传递函数辨识结果的优劣。仿真中, 系统单位冲激响应函数用中心频率为1, 2, 4和8 kHz的高斯脉冲相加模拟。
图 3给出了上述条件下的测量系统传递函数辨识结果。由图可知, 本文所述2种系统辨识方法均可有效获取测量系统的传递函数。但方法1对信噪比有一定要求。当信噪比大于30 dB时辨识结果精度较高; 而方法2系统辨识结果优于方法1, 在信噪比较低情况下依然能够获得高精度的辨识结果。这是因为背景噪声与声源激励信号相关性较小, 因此该方法有一定的抗噪能力。下面通过仿真与数值计算分析本文所述测量方法的有效性。
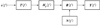 |
图 1 接收信号模型示意图 |
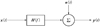 |
图 2 系统辨识示意图 |
 |
图 3 发射换能器传递函数辨识结果 |
1.2 观测数据处理
1) 获取观测数据。测量原理图如图 4所示。图中, ri为直达声声程, 矢量水听器到试样距离为d, 反射声声程为ri+2d, re=rs+rr为衍射声声程, rq为水池边界反射声声程, pi为直达声, pr为反射声, pe为试样边缘衍射声, pq为多途干扰声。
设发射换能器激励信号频谱为s(f), 忽略介质特性阻抗。不失一般性, 二维矢量水听器接收信号的频域表达式为
式中, Rs(f)为依赖于声波频率与入射角度的试样声反射系数, D(f)为试样边缘衍射系数, Rq(f)为水池边界反射系数, τr, τe和τq分别为反射声、试样边缘衍射声和水池边界反射声与直达声的时延, θi, θr, θe和θq分别为直达声、反射声、试样边缘衍射声和水池边界反射声的声波入射角度, Hpt(f), Hvxt(f)与Hvxt(f)分别表示测量系统各个测量通道的传递函数。
2) 测量系统传递函数补偿。将设计逆滤波器与相应通道观测数据频谱相乘, 得到补偿后的信号频谱Ppost(f), Vxpost(f)和Vypost(f)为
仿真条件2 设水池深度为10 m, 发射换能器、矢量水听器与待测试样下水深度h为5 m。发射换能器到试样距离H为15 m, 矢量水听器到试样距离d为10 cm, 发射信号为巴特沃兹脉冲声信号, 信号带宽为500~10 kHz, 采样频率fs=131 072 Hz, 信噪比为30 dB, 以声压通道为例, 验证后置逆滤波补偿的有效性。仿真中, 待测试样为铝板, 板厚0.006 m, 几何尺寸为1 m×1 m, 试样边缘衍射系数用低通滤波器模拟。
图 5给出了声压通道后置逆滤波的补偿效果, 由图可知补偿后信号波形更加规则、平滑, 有效抑制了测量系统传递函数引起的信号失真, 利于剔除边缘衍射声等干扰。
3) 剔除干扰声。根据测量系统布放参数计算反射声、试样衍射声和水池边界反射声时延, 将(9)式进行傅里叶反变换, 得到时域信号, 再加窗截取有用信号, 并进行傅里叶变换, 得到
式中, Pc(f), Vxc(f)和Vyc(f)分别为剔除干扰后的各个通道信号频谱。
4) 分离直达声与反射声, 获取试样声反射系数。设矢量水听器引导方位为ψ, 计算合成质点振速Vc为
首先将引导方位指向发射换能器, 即令ψ=0, 并进行(p+vc)2联合处理, 省略公共项s(f), 得到联合处理输出Ii为
再将引导方位指向试样, 即令ψ=π, 并进行(p+vc)2联合处理, 得到联合处理输出Ir为
易见
仿真条件保持不变, 对比分析采用后置逆滤波技术与未采用后置逆滤波技术的测量结果, 验证测量的有效性, 测量结果如图 6所示。
由图 6可知采用后置逆滤波技术后测量精度显著提高, 证明了该方法的有效性。综上, 基于单矢量水听器和后置逆滤波技术的水声材料法向声反射系数测量流程如图 7所示:
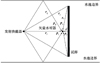 |
图 4 测量原理示意图 |
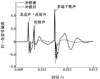 |
图 5 后置逆滤波补偿效果 |
 |
图 6 测量结果 |
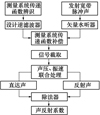 |
图 7 测量流程图 |
2 测量误差分析
仿真条件3 测量系统参数不变, 发射信号为巴特沃兹脉冲声信号, 信号带宽为500~10 kHz, 在不考虑试样边缘衍射效应以及水池边界反射声影响的条件下, 讨论信噪比分别为20, 30和40 dB时测量结果随频率的变化规律。
图 8出了不同信噪比情况下测测量结果和测量相对误差曲线。由图可知, 测量相对误差随频率震荡衰减, 低频段受信噪比影响较大; 另外, 当信噪比为20 dB时, 测量结果变化趋势与理论值相同, 但测量结果误差较大; 低频段测量误差较大是因为声反射系数很小, 较小的波动即可造成较大的相对误差。
在实际测试中, 除信噪比以外, 测量系统布放误差也会对测量结果造成影响, 下面仿真分析测量系统布放误差的影响。
仿真条件4 测量系统参数不变, 不考虑背景噪声以及试样边缘衍射等干扰, 声源到试样距离H分别为5, 10和15 m, 讨论当矢量水听器到试样距离d存在10%误差时的测量结果。
图 9给出了发射换能器到试样距离H不同、矢量水听器到试样距离d存在10%误差时测量结果, 由图可知测量结果对矢量水听器到试样距离误差不敏感; H不同时测量结果几乎重合, 可知在实际测试中只需根据测量水池几何尺寸选择合适H即可。
仿真条件5 测量系统参数保持不变, 不考虑背景噪声以及试样边缘衍射等干扰, 矢量水听器到试样距离d分别为5, 10和15 cm, 发射换能器到试样距离H为15 m, 讨论当发射换能器到试样距离H存在1%误差时的测量结果。
图 10给出了矢量水听器到试样距离d不同、发射换能器到试样距离H存在1%误差时测量结果, 由图可知测量结果与理论值随频率变化趋势相同, 并且频率越高测量结果越准确, 且本测量方法对矢量水听器到试样距离误差不敏感。
由上述仿真和数值分析结果可见, 本文所示方法可有效实现水声材料法向声反射系数的自由场大样测量, 并且该方法对测量环境与测量系统布放精度较宽容, 证明了本方法的可行性。
 |
图 8 测量结果 |
 |
图 9 测量结果(d存在10%误差) |
 |
图 10 测量结果(H存在1%误差) |
3 实验研究与数据处理
测量系统硬件组成框图如图 11所示, 系统由干端与湿端构成。其中干端主要由任意信号发生器、功率放大器、矢量水听器调理电路和信号采集器等构成, 用于信号生成、发射和采集。湿端主要由发射换能器、低频二维矢量水听器和试样等构成, 用以测量试样。湿端布放于几何尺寸为25 m×15 m×10 m的消声水池中, 声中心位于水下5 m处。水池六面消声, 吸声下限为2 kHz。待测试样是几何尺寸为1 m×1 m×0.006 m的铝板, 发射换能器吊放于水池上方行车边缘, 到试样距离H为4.95 m。试样固定在升降回转装置上, 测量中试样可旋转角度, 并平稳三维移动。矢量水听器布放于试样前端, 到试样表面距离d为5.5 cm。发射换能器为柱形声源, 图 12为其发送电压响应曲线。
由图 12可知, 发射换能器2.5 kHz以下辐射能力较差。低频二维矢量水听器有效工作频段为1~12 kHz。布放时, 矢量Vy通道指向待测试样, Vx指向水池池壁。首先发射16阶伪随机序列辨识测量系统传递函数, 并设计逆滤波器。图 13给出了测量系统传递函数辨识结果, 图中hp(f)、hvx(f)和hvy(f)分别为测量系统声压通道、矢量Vx通道与Vy通道的传递函数测量值; hpinv(f)、hvxinv(f)和hvyinv(f)分别为设计的逆滤波器传递函数。
由图 13可知, 矢量Vx通道传递函数辨识结果失效, 这是因为在上述布放情况下, 矢量水听器Vx通道的“凹点”正对声源, 该通道接收到的信号仅有水池池壁反射声信号, 因此系统辨识结果不准确。
保持发射换能器与矢量水听器空间位置与指向不变, 放下试样, 发射带宽为500~12.5 kHz的巴特沃兹脉冲声信号。图 14给出了矢量水听器各个通道接收到的原始数据与修正后的信号波形。
由图 14可见, 逆滤波修正后的信号时域波形变得规则, 能量更加集中。再根据测量系统空间布放参数计算直达声与反射声、试样边缘衍射声的时延, 并加窗截取有用数据, 计算试样法向声反射系数如图 15所示。
图 15给出了补偿前后测量结果, 可见未补偿测量系统传递函数的测量结果误差很大, 几乎失效, 而经后置逆滤波处理后测量精度大幅提升。当频率大于2.5kHz时, 后置逆滤波修正后测量误差较小, 而2.5kHz以下测量结果误差较大。究其原因是由于发射换能器低频发射能力有限, 信号低频段成分淹没于背景噪声中, 因此测量结果较差。
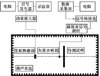 |
图 11 测量系统硬件组成 |
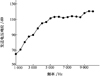 |
图 12 发射换能器发送电压响应曲线 |
 |
图 13 测量系统传递函数辨识与逆滤波器设计结果 |
 |
图 14 逆滤波效果对比 |
 |
图 15 逆滤波效果对比 |
4 结论
本文提出了一种基于单矢量水听器的水声材料法向声反射系数自由场大样测量方法。该方法将脉冲声发射技术、矢量信号处理技术与后置逆滤波技术相结合, 通过后置逆滤波技术对矢量水听器接收数据进行补偿, 抑制由于测量系统传递函数引起的信号失真, 在时域上剔除试样的边缘衍射声与多途信号的干扰, 提高测量精度。理论推导了测量原理, 通过数值计算与仿真研究了测量系统误差等的影响, 并开展了实验研究, 数值计算与仿真结果表明本文所述测量方法对信噪比有一定要求; 另外该方法对测量系统布放不准确不敏感。实验结果表明本文所述方法可有效实现水声材料法向声反射系数的自由场大样测量, 但受发射换能器低频辐射能力的限制, 低频段测量误差较大。
References
- Zheng Shijie, Yuan Wenjun, Miao Rongxing, et al. The Measurement Technology of Underwater Acoustic[M]. Harbin, Harbin Engineering University Press, 1995 (in Chinese) [Google Scholar]
- Chen Yi, Yuan Wenjun, Zhao Han. Investigation on the Sound Pulse Transient Suppression Method Used in the Underwater Acoustic Measurement[J]. Applied Acoustics, 2002, 21(4): 10–15 [Article] (in Chinese) [Google Scholar]
- Li Shui, Miao Rongxing. Measurements for the Properties of Underwater Acoustic Materials by Broadband Compressed Pulse Super Position Method[J]. Acta Acoustica, 2000, 25(3): 248–253 [Article] (in Chinese) [Google Scholar]
- Dai Yang, Yang Jianhua, Hou Hong, et al. The Absorption Coefficient Measuement of the Underwater Material in Water Tube with the Wide-Band Pulse Method[J]. Acta Acoustica, 2017, 42(4): 476–484 [Article] [Google Scholar]
- Lanoye R, Bree D H E, Lauriks W. A Practical Device to Determine the Reflection Coefficient of Acoustic Materials in Situ Based on a Microflown and Microphone Sensor[J]. ISMA, 2004, 1/2/3/4/5/6/7/8: 2665–2675 [Article] [Google Scholar]
- Lanoye R, Vermeir G, Lauriks W. Measuring the Free Field Acoustic Impedance and Absorption Coefficient of Sound Absorbing Materials with a Combined Particle Velocity-Pressure Sensor[J]. Acoust Soc Am, 2006, 119(5): 2826–2831 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Kunikazu Hirosawa, Kazuhiro Takashima, Hiroshi Nakagawa, et al. Comparison of Three Measurement Techniques for the Normal Absorption Coefficient of Sound Absorbing Materials in the Free Field[J]. J Acoust Soc Am, 2009, 118: 3020–3027 [Article] [CrossRef] [Google Scholar]
- Chen Hongjuan. The Vector Sensors[M]. Harbin, Harbin Engineering University Press, 2006 (in Chinese) [Google Scholar]
- Shi Shenguo. Research on Vector Hydrophone and Its Application for Underwater Platform[D]. Harbin, Harbin Engineering University, 2006 (in Chinese) [Google Scholar]
- Bendat J S, Piersol A G. Engineering Applications of Correlation and Spectral Analysis[M]. Ling Fugen, Translator. Beijing, National Defense Industry Press, 1980 (in Chinese) [Google Scholar]
- WangZuomin. The Period Pseudorandom Sequence Signal and Applied in the Acoustic Measurement[J]. Noise and Vuberation Control, 1993, (4): 2–4 [Article] [Google Scholar]
- Dai Yang, Yang Jianhua, Hou Hong. Sound Pulse Generation Using the Post-Processing Inverse Filter[J]. Noise and Vuberation Control, 2014, 31(suppl 1): 464–466 [Article] [NASA ADS] [Google Scholar]
All Figures
 |
图 1 接收信号模型示意图 |
| In the text | |
 |
图 2 系统辨识示意图 |
| In the text | |
 |
图 3 发射换能器传递函数辨识结果 |
| In the text | |
 |
图 4 测量原理示意图 |
| In the text | |
 |
图 5 后置逆滤波补偿效果 |
| In the text | |
 |
图 6 测量结果 |
| In the text | |
 |
图 7 测量流程图 |
| In the text | |
 |
图 8 测量结果 |
| In the text | |
 |
图 9 测量结果(d存在10%误差) |
| In the text | |
 |
图 10 测量结果(H存在1%误差) |
| In the text | |
 |
图 11 测量系统硬件组成 |
| In the text | |
 |
图 12 发射换能器发送电压响应曲线 |
| In the text | |
 |
图 13 测量系统传递函数辨识与逆滤波器设计结果 |
| In the text | |
 |
图 14 逆滤波效果对比 |
| In the text | |
 |
图 15 逆滤波效果对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


