| Issue |
JNWPU
Volume 37, Number 6, December 2019
|
|
|---|---|---|
| Page(s) | 1148 - 1157 | |
| DOI | https://doi.org/10.1051/jnwpu/20193761148 | |
| Published online | 11 February 2020 | |
Effects of Shear Layer Characteristics on Acoustic Propagation and Source Localization
剪切层形态对声波传播与声源定位的影响研究
1
School of Aerospace Engineering, Xiamen University, Xiamen 361102, China
2
Key Laboratory of Aerodynamic Noise Control, China Aerodynamics Research and Development Center, Mianyang 621000, China
Received:
5
December
2018
The shear layer characteristics of an open-jet acoustic wind tunnel are of key importance on measurements of aeroacoustics. The effects of thickness, spreading angle and strength of shear layer on acoustic propagation and source localization are investigated through the mean/spreading shear layer with a self-similar velocity distribution. Based on the shear flow, the acoustic propagation is computed by the linearized Euler equations via a source term, and then source localization is obtained from beamforming technique combined with the theory of Amiet. Results show that the numerical method can precisely capture the refraction and reflection after sound traversing shear layer. The thickness, spreading angle and strength of the shear layer exerts little effects on the refracted region where sound wave nearly vertical incident, while mainly influence the corresponding up/downstream region in terms of phase change. Increment of thickness, spreading angle and strength of the shear layer increases the acoustic difference between the shear layer with and without thickness, and produces a larger error of source localization downstream of the actual position.
摘要
声学风洞开口实验段的剪切层形态对气动噪声测量及声源定位有重要影响。以平行剪切层和扩张剪切层为对象研究了剪切层的厚度、扩张角、强度等因素对声波穿过剪切层传播规律以及声源定位的影响。剪切层的流场采用自相似的速度分布来构造,声传播模拟采用带源项的线化欧拉方程,声源定位使用基于Amiet理论的波束成形技术。研究结果表明:采用高精度的数值方法可以很好模拟声波穿过剪切层产生的折射、反射等现象;剪切层厚度、扩张角和强度等的变化对使用简化对流波动方程预测的垂直入射区影响较小,对上/下游区域影响较大,这主要体现在剪切层的存在改变了声传播的相位;剪切层厚度、扩张角和强度的增加,造成声波穿过有/无厚度剪切层的声场差别增大、基于Amiet理论定位的声源相对实际声源的位置偏移量增大。
Key words: aeroacoustics / wind tunnel / shear layer / refraction / source localization
关键字 : 气动声学 / 风洞 / 剪切层 / 折射 / 声源定位
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
声学风洞是研究气动噪声产生机理和传播规律的重要工具。开口式风洞因高信噪比、可获取远场气动噪声特性等优势,成为一种应用较广的测量方式[1-3]。但是,开口风洞射流与静止空气会形成剪切层,使声波穿过剪切层产生折射、反射与散射等现象,研究表明该现象是影响气动噪声测量和声源定位精度的主要因素[4]。因此,深入理解声波在剪切层中的传播规律,对提高气动噪声的测量精度至关重要。关于声波穿过剪切层的传播规律,许多学者从理论、实验和数值模拟等方面研究了声波与剪切层的相互作用。Padois等[5]忽略剪切层的速度梯度,通过简化对流波动方程,修正了对流引起的声源偏移。当考虑剪切层折射时,Amiet[6]基于无厚度假设,预测了声波穿过剪切层后方向与幅值的变化。该方法适用任意声源类型,其趋势被大量实验验证[7-10]。后续研究进一步引入偏心轴声源[11]、温度梯度[12]、分层模型[13-14]与风洞出口形状[15]等因素。
在数值模拟方面,邢超[16]仿真了单极子声波穿过剪切流的现象。张雪等[17]使用线化欧拉方程(linearised Euler equation,LEE)模拟了声波穿过无厚度风洞剪切层的声场,并将计算得到的延迟时间与压比同Amiet理论相互验证。Bogey等[18]数值验证了用声源源项模拟声传播的合理性,并对比了线化欧拉方程有无简化时的折射现象。Redonnet等[19]基于计算气动声学(computational aero acoustic,CAA)和几何声学研究了马赫数0.17下不同剪切层对声波传播的影响。文献[20]借助有限元法对声波穿过轴对称射流进行了研究。Bennaceur等[21]使用大涡模拟讨论了三维空间发展剪切层下声波的频谱展宽效应。
目前国内外关于剪切层参数对声波在剪切层中传播和声源定位的影响研究还很少,并且理论和实验研究难以获得声波穿过不同剪切层后的整个声场,同时现有的数值模拟也很少考虑仿真的声源信号对声源定位的影响。因此,本文将借助CAA高精度数值模拟方法和基于波束成形的声源定位技术,重点研究剪切层参数对声波传播与声源定位的影响规律。本文首先基于剪切层的自相似特性[10, 22-23],以平行剪切层为对象研究剪切层厚度,以扩张剪切层为对象分析扩张角,同时考虑剪切层强度对声波传播的影响,系统分析了剪切层引起的声场参数变化。然后使用Amiet理论研究不同剪切层下的声源定位,对比定位声源与给定声源的位置差,得到用Amiet的无厚度假设在平行/扩张剪切层中的误差,以期为声学风洞的修正提供参考。
1 数值方法及验证
1.1 声场控制方程
声波传播的模拟采用二维的线化欧拉方程,该方程考虑非均匀流场对声波传播的影响,形式为
式中, U为未知向量, E, F和H为通量向量, S表示声源源项, 各表达式如下:
式中,ρ′, u′, v′, p′分别表示声场中密度、x方向速度、y方向速度、压强的扰动量, 下标“0”表示背景流场的平均量。ρ′S与p′S用于构造单极子声源, 假设等熵、不考虑温度梯度, 可得p′S=ρ′S/c02。由于线化欧拉方程支持不稳定涡波与熵波的传播, 并且欧拉方程的非线性项已经被省略, 容易造成不稳定波成倍增长与计算发散, 因此声场数值模拟忽略H项[18]以消除上述因素的影响。
1.2 声场数值方法
数值方法详见文献[24], 控制方程采用高阶中心差分求解, 每波长至少10个网格节点以保证精度。空间离散使用7点4阶的色散关系保持(dispersion-relation-preserving, DRP)格式, 并借助11点10阶滤波器消除高频振荡。时间离散采用低耗散低色散的优化5步龙格-库塔显式时间推进格式。远场无反射边界在计算域外添加6层指数型增长的虚拟网格作为缓冲区, 让扰动在该区域内被耗散, 从而达到无反射的效果。
1.3 声场算例验证
数值验证采用单极子声源在剪切层中传播算例[18]。速度分布拟合自大涡模拟的时均流场
式中,u01=0.118, u02=0.470, δw(x)表示涡量厚度。
声源形式为
式中,圆频率w=2πc0/λ, 波长λ=51.5, 声源幅值ε=10-4, Δ=0.24, 无量纲音速c0=1, 声源坐标(xS, yS)=(70, 0)。
具体无量纲形式如下:
式中等号左边为无量纲值, 右边变量中上标“*”表示实际值, 下标“ref”表示参考值。
背景流场压力p0=1/γ、密度ρ0=1, 计算域(0≤x≤300, -200≤y≤200)包括501×501网格节点, 且分别沿xy方向均匀分布。无量纲时间步长为Δt=0.1。图 1a)为t=599.8时的瞬时压力云图。参见文献[18], 本文计算声场整体吻合, 仅在边界附近出现小幅反射。图 1b)提取图 1a)中x=0和x=300的瞬时压力曲线与文献[18]作对比, 结果吻合良好。
 |
图1 声波在剪切流中传播的验证 |
1.4 Amiet理论
声学风洞常用Amiet理论[6]修正剪切层对声线轨迹的偏转。假设剪切层无厚度、无温度梯度、两侧介质稳定均匀, 可得到图 2所示的基于二维Amiet理论的声传播原理图。
已知声源点S(xS, yS)、剪切层上一点B(xB, yB)以及麦克风O(xO, yO)。由图中几何关系可知
根据对流Snell定律可知
式中
由(6)至(7)式即可迭代出θ′与θ, 再计算出xB即可获得声线SBO的传播时间为t=t1+t2。根据费马原理可知, 该传播时间t最小。
式中, u01表示剪切层下方气流速度。
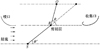 |
图2 开口式风洞中声波传播示意图 |
1.5 声源定位
风洞定位过程中, 声源坐标未知, 一般事先预设一个扫描平面, 将扫描平面上的扫描点视为可能的声源点。然后由1.4节依次求出单个扫描点到每个麦克风的声传播时间, 并以某一麦克风的时间为基准, 获得其他麦克风的延迟时间。最后将考虑延迟时间后的麦克风信号叠加,取最大值作为该扫描点的信号值。具体过程为
式中,下标“s”和“m”分别表示扫描平面与虚拟麦克风阵列。p′s表示扫描点的声信号, ωm为不同麦克风权重, p′m为麦克风接收到的信号, Δm为对应扫描点与麦克风的延迟时间。
本文采用单个点声源, 扫描平面上扫描点信号p′s的最大值就是声源位置。此外, “虚拟麦克风”采用线阵列, 取x方向的501个网格节点, 网格间距满足识别信号所需的1/2波长要求[5]。本文的数据量小, 不考虑互谱矩阵, 也未对数据分块处理。
2 计算模型
声源模型通常靠近风洞出口, 忽略上下剪切层相交以及模型尾流对剪切层演化的影响。剪切层位于y=0, 不考虑y方向速度, 忽略流向演化的旋涡。计算域为-0.7≤x≤0.7, -0.5≤y≤0.9, 网格节点数与1.3节相同, 节点间距为Δx=Δy=0.002 8。声源坐标(0, -0.3), 长度无量纲参数Lref=1 m, 时间步长Δt=0.001。CAA计算采用混合方法, 声场四周采用无反射边界, 且流场与声场用同一套网格。
风洞剪切层采用Görtler的自相似速度分布[23]
式中,erf表示高斯误差函数。
式中,σ0为扩张因子, 范围9.0~13.5;xsh控制有无扩张角。xsh=0.7时, 表示平行剪切层, xsh为变量时, 表示扩张剪切层。ξ0用于考虑风洞出口尾缘厚度的影响。
图 3展示了不同形式的剪切层。当σ0→∞时, 如图 3a)所示, 为理想状态的无厚度剪切层。当xsh=0.7、σ0=11.0时, 图 3b)所示为有厚度的平行剪切层。图 3c)表示对应的扩张剪切层。若定义u0/u01为0.05和0.95为剪切层的边界, 则剪切层厚度为δx=|y0.05-y0.95|, 扩张角θx即为两边界的夹角。
 |
图3 3种形式剪切层的x方向速度云图 |
3 剪切层参数对声传播的影响
3.1 无厚度剪切层的声场特征
无厚度剪切层中M=0.2, δx=0.0(对应σ0=∞)。声源采用(4)式的单极子形式, ε=0.01, Δ=0.005, 频率为f*=5 kHz, 对应的无量纲圆频率ω=92.4。声波波长0.068的4倍小于声源至剪切层的距离0.3倍, 满足文献[9]的远场假设。
图 4表示t=3时, 声波穿过无厚度剪切层的压力脉动。由图可知, 当声波未到达剪切层时, 由于多普勒效应, 声波分别以马赫数1∓M向上游和下游传播, 逆气流方向传播的声波被压缩, 波长变短, 频率增大; 顺气流方向传播的声波波长变长, 频率减小。随着传播距离的增加, 声波的幅值逐渐减弱。根据Amiet理论可知, 声波穿过剪切层传播方向会偏转, 并且当入射角大于临界入射角, 即折射角大于90°时, 声波会发生全反射现象。从图中可知, 当声波穿过剪切层后发生折射, 且在剪切层下方、声源的上游出现了明显的声波反射现象。同时由于剪切层上方气流静止, 声波传播的多普勒效应逐渐消失。
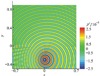 |
图4 t=3时,声波在无厚度剪切层(δx=0.0)中的瞬时压力图 |
3.2 剪切层厚度对声传播的影响
为了研究剪切层厚度对声波传播的影响, 本文对比了马赫数M=0.2, δx=0.251, 0.296和0.362(对应σ0=13.0, 11.0与9.0)的平行剪切层与无厚度剪切层的声场差异。所用声源与3.1节相同。
图 5表示剪切层厚度δx=0.296与δx=0.0的声场差值。从图中可知, 两者在声源上方比较接近, 差别主要集中在上游, 部分出现在下游。此外, 声源上游、剪切层上下两侧的差值条纹出现相位差。上述原因有两方面:一是平行剪切层相当于多层均匀流动的介质, 相邻介质的速度梯度造成声传播方向多次偏转[13], 改变了声波的幅值与相位, 最终造成声源上下游的差值区域较大。二是声源上方附近的入射波方向与剪切层垂直, 受折射和反射影响较小, 所以厚度变化造成的声场差别较小。
当不存在风洞射流时, 声波波阵面垂直入射的位置在声源正上方; 随着射流速度的增加, 波阵面垂直入射的位置会向下游偏移。根据简化对流波动方程[5]可近似得到垂直入射位置为
式中,xS为声源横坐标, h为声源与剪切层的距离。此处xnom=0.06, 对应图 5中的虚线位置。
图 6提取了不同厚度剪切层声场中y=0.6处的瞬时压力差值。图中黑点坐标为(xnom, 0.0), 其与曲线相交, 表明在xnom处确实差别较小。由图可知, 压力曲线在xnom附近波动范围较小, 在两侧的波动范围较大, 这一结果与图 5一致。此外, 越靠近x=-0.7和x=0.7, 波动范围越大。对比不同厚度的压力曲线可知, 厚度的增加会加剧两侧的波动, 但对xnom附近区域影响较小。
图 7为剪切层上方3个监测点压力的时间序列。图 7a)为上游测点, 由图可知, 不同厚度剪切层中监测到的声压信号幅值接近, 但存在相位偏移。随剪切层厚度增加, 相位偏移量变大。图 7b)为垂直入射位置测点, 从中监测的压力信号差别不大。图 7c)为折射区下游测点, 其随着剪切层厚度增加, 相位偏移量同样变大, 但偏移方向与图 7a)相反。
综上可知, 剪切层厚度主要改变上下游的声场, 对xnom附近声场影响较小。不同厚度主要引起折射区中声信号的相位偏移, 幅值影响的比重较小。
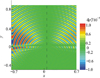 |
图5 t=3时,厚度为0.296与无厚度剪切层的声场瞬时压力差值(虚线表示声波波阵面垂直入射位置) |
 |
图6 t=3时,不同厚度的平行剪切层瞬时压力差值曲线 |
 |
图7 不同厚度剪切层的中压力脉动随时间的变化曲线 |
3.3 剪切层扩张角对声传播的影响
为了研究剪切层扩张角对声波传播的影响, 本文分别计算了M=0.2, 扩张角θx=10.2°, 12.2°和14.7°(对应σ0=13.0, 11.0, 9.0)的扩张剪切层与无厚度剪切层的声场差异。声源与3.1节相同。
图 8表示扩张角θx=12.2°的扩张剪切层与无厚度剪切层的声场差值。两者在垂直入射位置xnom=0.06附近的区域差别较小, 在两侧差别较大。与图 5不同, 差别区域主要集中在下游, 部分出现在上游, 其原因有两方面:一是扩张角的存在改变了剪切层厚度。由图 3可知, 扩张剪切层在x=-0.7处与无厚度剪切层相同, 在x=0.7处与对应σ0的平行剪切层厚度相同。因而, 在上游差别小, 下游差别大。另一方面扩张剪切层改变了声波入射角, 同样会影响声波的折射与反射。
为了分析扩张角的影响, 图 9展示了y=0.6处不同扩张剪切层中声场压差曲线。由图可知, 在垂直入射位置的附近波动较小, 在两侧波动较大, 下游波动范围大于上游, 且扩张角越大, 波动越大。
图 10表示用正弦函数p′=p′asinωt+Ph拟合y=0.6处不同监测点的声压曲线, 得到不同扩张剪切层与无厚度剪切层的振幅差dp′a和滤波后的相位差dPh。从图 10a)可知, 扩张剪切层与无厚度剪切层的声压幅值总体差别不大, 仅在声源下游有小幅波动, 且所选扩张角10.2°~14.7°的振幅接近。从图 10b)可知, 扩张剪切层和无厚度剪切层的声场存在明显相位差, 且近似呈线性, 其在xnom=0.06处较小, 接近于0;在两侧较大, 且上下游相位差正负相反。随着扩张角的增大, 相位差曲线斜率增加。
综上可知, 剪切层扩张角主要改变声源上下游的声场, 对垂直入射区的声场影响较小。扩张角主要影响声信号的相位偏移, 对振幅影响较小。扩张角越大, 相位偏移越大。
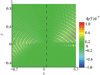 |
图8 t=3时,扩张角12.2°的剪切层与0°剪切层的声场瞬时压力差值图 |
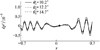 |
图9 t=3时,不同扩张角的扩张剪切层瞬时压力差值曲线 |
 |
图10 y=0.6处不同扩张角剪切层与无厚度剪切层的差值图 |
3.4 剪切层强度对声传播的影响
为了研究剪切层强度对声波传播的影响, 本文进一步计算了Ma=0.1与0.4时不同剪切层的声传播情况。
图 11表示不同马赫数下的压力差值。其中图 11a)表示马赫数Ma=0.1下平行剪切层与无厚度剪切层的声压差。从图中可知, 低马赫数下有/无厚度的差别较小。图 11b)则表明马赫数增加会扩大平行剪切层与无厚度剪切层的声场差别, 使得条纹区增大。
图 11c)为扩张剪切层在马赫数Ma=0.1下与无厚度剪切层的声场差值。由图可知, 差别区域主要集中在声源点下游, 在上游并未出现图 11a)中明显的条纹。图 11d)为Ma=0.4时的声场差值。随着马赫数的增加, 声源上下游的条纹区域扩大。与图 11b)对比可知, 在声源下游条纹较接近, 在声源上游两者存在明显区别, 扩张剪切层上游条纹较弱。
综合图 5、图 8与图 11可知, 在声源上方总是存在一个厚度与扩张角影响较小的区域。在该区域内, 平行/扩张剪切层的声信号与无厚度剪切层接近。(11)式的规律在不同马赫数下仍然合理, 其计算的垂直入射位置大致位于差别较小区域的中间。凭借这一规律, 在风洞实验中, 可根据经验预判一个声源位置, 然后将麦克风阵列的中心布置在垂直入射位置, 以提高定位的精度。实际声源位置可能有多个, 此时可考虑增大不同声源对应垂直入射位置的权重, 来提高定位精度。
与3.2和3.3节一致, 剪切层参数对幅值的改变仍较小, 因此不过多阐述。图 12为y=0.6处不同剪切层与无厚度剪切层的相位差值图, 从上游至下游的相位差近似呈线性。图 12a)为平行剪切层的相位差, 由图可知, 低马赫数下曲线斜率较小, 不同厚度的斜率接近。马赫数增大, 曲线的斜率增大, 不同厚度的曲线斜率差别增大。图 12b)为扩张剪切层的相位差, 从图中可以看到, 扩张角对斜率的影响规律与厚度相同。对比图 12a)与12b)可知, 平行剪切层上游的相位差明显大于扩张剪切层, 下游两者较接近。这一趋势与图 11一致。
 |
图11 t=3时, 不同马赫数的剪切层与无厚度剪切层的压力差值 |
 |
图12 t=3时, y=0.6处不同剪切层在不同马赫数下的相位差 |
4 剪切层参数对声定位的影响
在风洞实验中, 相位差并不影响均方根等独立于相位的变量, 即不影响指向性。但相位差表征延迟时间差, 会影响声源定位精度。通过第3节的介绍可知, 厚度与扩张角的存在会使平行/扩张剪切层的声信号与无厚度剪切层中的信号产生相位差。若仍用Amiet的无厚度假设修正, 会导致定位出现误差。为评估Amiet理论在不同剪切层中的定位误差, 本节使用第3节中模拟的声信号进行定位, 对比了定位声源位置与实际声源位置的偏移量。
4.1 剪切层厚度对声源定位的影响
图 13为Ma=0.2时不同厚度剪切层的波束, 波束形式与文献[5]相似, 包含一个主瓣和许多旁瓣, 主瓣峰值无量纲化为1, 其x坐标为定位出的声源位置。定位声源与实际声源xS=0的距离为定位误差xshift。由图可知, Amiet理论对无厚度剪切层中的声源定位较准, 随厚度增加, 声源位置向下游偏移。
 |
图13 不同厚度剪切层下用Amiet理论的声源定位波束 |
4.2 剪切层扩张角对声源定位影响
图 14为Ma=0.2时不同扩张剪切层下的声波波束。由图可知, 扩张角的存在, 会使定位的声源位置向下游偏移, 且随着扩张角的增加, 声源位置不断下移。对比图 13与图 14可知, 相同σ0的条件下, 平行剪切层引起的声源偏移大于扩张剪切层。
 |
图14 不同扩张剪切层下用Amiet理论的声源定位波束 |
4.3 剪切层强度对声源定位影响
表 1为不同马赫数下平行剪切层与扩张剪切层的声源定位。从表中可以看出, 不同马赫数下, 无厚度剪切层中的定位都较准, 位置偏移量随马赫数的增大而略微增加, 但基本接近给定声源。考虑厚度与扩张角后, 声源位置开始向下游偏移, 且偏移量明显大于无厚度剪切层。不同马赫数下, 剪切层厚度和扩张角对声波传播的规律相似, 但是其影响随马赫数的增大而增强。文献[17, 25]中的实验结果也表明Amiet理论的修正偏差随马赫数增大而增大。因此, 对于马赫数较高和风洞尺寸更大的情况, 有必要考虑剪切层参数的影响。
不同马赫数下使用Amiet理论定位声源的位置xshift
4.4 剪切层参数对声源定位影响
为了进一步分析剪切层对声源定位的影响, 引入斯特劳哈尔数Sr来表征剪切层形态与声波波长λ的关系。
式中,Lavg表示剪切层平均厚度。
图 15将表 1中的参数转换为Sr·Ma与声源位置偏移量xshift的关系。由图可知, 其趋势基本呈线性关系, 可线性拟合为xshift=0.013 9Sr·Ma。这表明声源偏移量随剪切层厚度、扩张角和强度的增大而增大, 与前面小节介绍的趋势一致。此外, 本次基于Sr与Ma进行拟合的思路也可以借鉴于实际工程应用。
 |
图15 声源位置偏移量随Sr·Ma变化的趋势 |
5 结论
本文基于自相似的剪切层速度分布,对声波穿过剪切层的传播现象进行了数值模拟,重点研究了所构造剪切层的厚度、扩张角、强度等对声波穿过剪切层的传播规律和声源定位精度的影响,可以得到以下结论:
1) 剪切层的厚度主要影响声源上/下游靠近剪切层的区域,对简化对流波动方程预估的垂直入射区影响较小。剪切层厚度使得麦克风测量的声信号产生相位偏移,导致定位声源的位置比实际声源位置更向下游方向偏移。
2) 剪切层的扩张角也会产生相位偏移,导致定位声源的位置比实际声源位置更向下游方向偏移,但扩张角引起声源的偏移量比相同厚度下平行剪切层引起的偏移量要小。
3) 剪切层的强度不影响垂直入射区的预估,也不改变由于厚度和扩张角对声传播和声源定位的影响规律,但随着剪切层强度的增强,剪切层的厚度与扩张角对声传播和声源定位的影响也增强。
References
- Oerlemans S, Broersma L, Sijtsma P. Quantification of Airframe Noise Using Microphone Arrays in Open and Closed Wind Tunnels[J]. International Journal of Aeroacoustics, 2007, 6(4): 309–333 [Article] [CrossRef] [Google Scholar]
- Yu Tao, Fan Jiechuan, Jia Yuansheng. The Present Situation and Development of Modern Aeroacoustic Wind Tunnel Technique[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(3): 86–91 [Article] (in Chinese) [Google Scholar]
- Zhang Jun, Chen Peng, Lei Hongsheng, et al. Influence of a 3/4 Open Jet Floor on Far Field Noise Measurements in Aeroacoustic Wind Tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2574–2582 [Article] (in Chinese) [Google Scholar]
- Sijtsma P, Oerlemans S, Tibbe T G, et al. Spectral Broadening by Shear Layers of Open Jet Wind Tunnels[C]//AIAA/CEAS Aeroacoustics Conference, 2014 [Google Scholar]
- Padois T, Prax C, Valeau V. Numerical Validation of Shear Flow Corrections for Beamforming Acoustic Source Localisation in Open Wind-Tunnels[J]. Applied Acoustics, 2013, 74(4): 591–601 [Article] [CrossRef] [Google Scholar]
- Amiet R K. Refraction of Sound by a Shear Layer[J]. Journal of Sound and Vibration, 1978, 58(4): 467–482 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Schlinker R H, Amiet R K. Refraction and Scattering of Sound by a Shear Layer[J]. The Journal of the Acoustical Society of America, 1981, 70(6): 1797–1799 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Ahuja K K, Tanna H K, Tester B J. An Experimental Study of Transmission, Reflection and Scattering of Sound in a Free Jet Flight Simulation Facility and Comparison with Theory[J]. Journal of Sound and Vibration, 1981, 75(1): 51–85 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Zhang Junlong, Li Zhengchu, Lu Xiangyu. Experimental Research on the Influence of Open Jet Shear Layer on Microphone and Microphone Array Measurement[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(1): 71–77 [Article] (in Chinese) [Google Scholar]
- Zhang Jun, Wang Xunnian, Zhang Junlong, et al. Shear Layer Correction Methods for Open-Jet wind Tunnel Phased Array Test[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(4): 39–46 [Article] (in Chinese) [Google Scholar]
- Morfey C L, Joseph P F. Shear Layer Refraction Corrections for Off-Axis Sources in a Jet Flow[J]. Journal of Sound and Vibration, 2001, 239(4): 819–848 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Dobrzynski W. Shear-layer Correction after Amiet under Consideration of Additional Temperature Gradient. Working Diagrams for Correction of Signals[R]. NASA 77741, 1984 [Google Scholar]
- Wang Yigang, Li Fangxu, Shen Zhe, et al. The Influence of Wind Tunnel Jet Flow and Airflow around Vehicle on Sound Propagation[J]. Technical Acoustics, 36(1): 57–63 [Article] (in Chinese) [Google Scholar]
- Shen Zhe, Wang Yigang, Yang Zhigang, et al. Acoustic Propagation Analysis of Jet Flow Based on Stratified Fan-Shaped Shear Layer Model[J]. Journal of Tongji University, 2017, 45(4): 596–601 [Article] (in Chinese) [Google Scholar]
- Porteous R, Geye T, Moreau D, et al. A Correction Method for Acoustic Source Localisation in Convex Shear Layer Geometries[J]. Applied Acoustics, 2018, 130: 128–132 [Article] [CrossRef] [Google Scholar]
- Xing Chao, Luo Jisheng. Numerical Simulation of Mixing Layer Effect on Sound Waves[J]. Journal of Aerospace Power, 2005, 20(1): 8–12 [Article] (in Chinese) [Google Scholar]
- Zhang Xue, Chen Bao, Lu Qinghua. Verification of Angle Refraction Correction Based on Amiet's Shear Layer Theory[J]. Journal of Applied Acoustics, 2014, 33(5): 433–438 [Article] (in Chinese) [Google Scholar]
- Bogey C, Bailly C, Juvé D. Computation of Flow Noise Using Source Terms in Linearized Euler's Equations[J]. AIAA Journal, 2002, 40(2): 235–243 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Redonnet S, Bulte J. Numerical Investigation of the Refraction Effects by Jet Flows in Anechoic Wind Tunnels, with Application to NASA/LaRC Quiet Flow Facility[C]//21st AIAA/CEAS Aeroacoustics Conference, 2015 [Google Scholar]
- Casalino D. Finite Element Solutions of a Wave Equation for Sound Propagation in Sheared Flows[J]. AIAA Journal, 2012, 50(1): 37–45 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Bennaceur I, Mincu D C, Mary I, et al. Numerical Simulation of Acoustic Scattering by a Plane Turbulent Shear Layer:Spectral Broadening Study[J]. Computers & Fluids, 2016, 138: 83–98 [Article] [CrossRef] [Google Scholar]
- Zhou Q, He F, Shen M Y. Direct Numerical Simulation of a Spatially Developing Compressible Plane Mixing Layer:Flow Structures and Mean Flow Properties[J]. Journal of Fluid Mechanics, 2012, 711: 437–468 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Yang Yin, Chen Yingchun, Li Dong. The Influence of Incompressible Shear Layer Inflow Conditions on Mixing Layer Development[J]. Journal of Northwestern Polytechnical University, 2017, 35(2): 197–202 [Article] [Article] [Google Scholar]
- Chen Rongqian. Hybrid Methods for the Computational Aeroacoustics Based on Acoustic Propagation Equations[D]. Nanjing, Nanjing University of Aeronautics and Astronautics, 2012 [Article] (in Chinese) [Google Scholar]
- Wang Y, Yang J, Jia Q, et al. An Improved Correction Method for Sound Source Drift in a Jet Flow and Its Application to a Wind Tunnel Measurement[J]. Acta Acustica United with Acustica, 2015, 101(3): 642–649 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 声波在剪切流中传播的验证 |
| In the text | |
 |
图2 开口式风洞中声波传播示意图 |
| In the text | |
 |
图3 3种形式剪切层的x方向速度云图 |
| In the text | |
 |
图4 t=3时,声波在无厚度剪切层(δx=0.0)中的瞬时压力图 |
| In the text | |
 |
图5 t=3时,厚度为0.296与无厚度剪切层的声场瞬时压力差值(虚线表示声波波阵面垂直入射位置) |
| In the text | |
 |
图6 t=3时,不同厚度的平行剪切层瞬时压力差值曲线 |
| In the text | |
 |
图7 不同厚度剪切层的中压力脉动随时间的变化曲线 |
| In the text | |
 |
图8 t=3时,扩张角12.2°的剪切层与0°剪切层的声场瞬时压力差值图 |
| In the text | |
 |
图9 t=3时,不同扩张角的扩张剪切层瞬时压力差值曲线 |
| In the text | |
 |
图10 y=0.6处不同扩张角剪切层与无厚度剪切层的差值图 |
| In the text | |
 |
图11 t=3时, 不同马赫数的剪切层与无厚度剪切层的压力差值 |
| In the text | |
 |
图12 t=3时, y=0.6处不同剪切层在不同马赫数下的相位差 |
| In the text | |
 |
图13 不同厚度剪切层下用Amiet理论的声源定位波束 |
| In the text | |
 |
图14 不同扩张剪切层下用Amiet理论的声源定位波束 |
| In the text | |
 |
图15 声源位置偏移量随Sr·Ma变化的趋势 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


