| Issue |
JNWPU
Volume 39, Number 4, August 2021
|
|
|---|---|---|
| Page(s) | 753 - 760 | |
| DOI | https://doi.org/10.1051/jnwpu/20213940753 | |
| Published online | 23 September 2021 | |
Multi-objective aerodynamic optimization of flying-wing configuration based on adjoint method
基于伴随方法的飞翼布局多目标气动优化设计
1
Shenyang Aircraft Design and Research Institute, Shenyang 110035, China
2
School of Aeronautics, Northwestern Polytechnic University, Xi’an 710072, China
Received:
6
November
2020
In order to solve the multi-objective multi-constraint design in aerodynamic design of flying wing, the aerodynamic optimization design based on the adjoint method is studied. In terms of the principle of the adjoint equation, the boundary conditions and the gradient equations are derived. The Navier-Stokes equations and adjoint aerodynamic optimization design method are adopted, the optimization design of the transonic drag reduction for the two different aspect ratio of the flying wing configurations is carried out. The results of the optimization design are as follows: Under the condition of satisfying the aerodynamic and geometric constraints, the transonic shock resistance of the flying wing is weakened to a great extent, which proves that the developed method has high optimization efficiency and good optimization effect in the multi-objective multi-constraint aerodynamic design of the flying wing.
摘要
针对飞翼布局气动设计中的多目标多约束设计问题，开展了基于伴随方法的气动优化设计研究。构建合理的统一目标函数，并根据伴随方法基本原理推导了相应的伴随方程边界条件及梯度求解方程，采用N-S方程和伴随气动优化设计方法，进行了2种不同展弦比飞翼布局的跨声速减阻优化设计，优化结果表明：在满足气动、几何约束的前提下，飞翼布局跨声速激波阻力被很大程度削弱，证明了所发展的方法在飞翼布局多目标多约束气动设计上具有较高的优化效率和良好的优化效果。
Key words: adjoint method / aerodynamic optimization design / multi-objective optimization / flying-wing configuration
关键字 : 伴随方法 / 气动优化设计 / 多目标优化 / 飞翼布局
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
目前结合数值模拟技术的气动外形优化设计方法主要分为两类：随机类方法和梯度类方法[1-2]。随机类方法追踪目标函数值相关信息，带有“随机”特性，具有全局性好、不要求设计变量连续分布以及导数存在等假设的优点，如遗传算法、代理模型方法等[3]，但其缺点是在采用N-S方程进行多设计变量的多目标气动设计时，CFD计算量巨大。尽管在过去几十年里计算机能力大大提高，但执行大量工程实际设计仍然不切实际，目前遗传算法应用仍局限于设计变量较少的设计问题；代理模型计算量相对遗传算法虽然有所减少，但其适用性受到设计变量取值范围和空间样本点分布的影响，不合理的设计变量及样本点分布将难以获得高精度的代理模型，从而导致设计结果偏离设计要求[4]。上述缺陷限制了随机类方法在多设计变量设计问题中的应用。
在梯度类方法中，基于伴随理论的气动优化设计方法(控制理论、共轭方法)在兼顾梯度的精确、快速求解和计算量方面取得较大的进步[1, 5]。其以偏微分方程系统的控制理论为基础，把物面边界作为控制函数，基于拉格朗日的观点将线化流动方程作为约束引入到目标函数与设计变量的表达式中，将设计问题转化为控制问题，计算量只相当于两倍流场计算量，与设计变量数目无关。国外采用伴随方法在翼型、机翼和翼身组合体乃至全机的气动优化设计中，取得了一系列的研究成果[5-11]。在国内，比较具代表性的是西北工业大学以乔志德教授为核心的团队，先后对翼型、机翼和翼身组合体开展了基于连续/离散伴随方法的Euler和N-S方程的优化设计，获得了比较满意的结果[12-14]；西安交通大学的丰镇平教授将伴随方法应用到内流领域的二维、三维透平叶栅气动优化设计中[1, 15]；西北工业大学白俊强团队近几年采用伴随方法在大型客机气动减阻和声爆特性优化方面做了研究[16-17]。总的来说，目前国内基于伴随方法在气动外形优化设计中取得了一些较为成熟的结果，提高了伴随方法在气动外形设计方面的工程应用前景，今后还将不断发展完善。
飞翼布局由于良好的气动效率及隐身特性，在军用飞机得到了广泛的应用，同时飞翼布局又存在操纵效能低，配平损失等典型问题[18]。所以无尾飞翼布局的气动外形设计是涉及总体、气动、控制、结构、隐身等专业约束的综合设计问题，即多目标多约束的设计问题。一般来说，要求飞机在巡航状态时具有较高升阻比，同时具有较小的低头力矩，从而不会引起较大的配平损失，而这两种要求往往是矛盾的，尤其在飞翼布局上表现的较为突出，即提高巡航升阻比的同时会带来较大的低头力矩。为了解决飞翼布局设计中的这种问题，本文基于伴随方法的基本原理，发展了一种考虑气动、结构约束的飞翼布局多目标多约束气动优化方法，并进行了典型算例验证。
1 流动控制方程
采用结构化贴体网格进行空间数值离散，并按照求和约定，在计算域中，N-S方程可表示为：
Fi=Sijfj; Fvi=Sijfvj; Sij=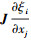
, J为物理域(x1, x2, x3)到计算域(ξ1, ξ2, ξ3)坐标变换的Jacobin矩阵, w表示流动物理量状态矢量, f为无黏矢通量, fv为黏性矢通量。
2 伴随方程及边界条件
2.1 伴随方法优化设计原理
气动优化问题是以外形变化对气动特性的影响为基础而进行的, 气动特性的目标函数可表述为:
dBξ, dDξ分别为计算空间中的表面与空间积分单元，M与P取决于流动变量w及计算空间的矩阵S。
在满足流场控制方程约束条件下, 气动外形的变化将导致流动变量变分δw与矩阵变分δS, 目标函数的变化可表示为
式中: δM=[Mw]Ⅰδw+δMⅡ, δP=[Pw]Ⅰδw+δPⅡ；下标Ⅰ表示由流动变量变化δw引起的贡献；下标Ⅱ表示由矩阵变化δS引起的贡献。
定常状态下, 气动外形变化的约束方程可表述为
引入伴随矢量ψ=(ψ1, ϕ1, ϕ2, ϕ3, θ)T, 与(4)式在整个计算空间求积, 则有
假定ψ可微, (5)式分部积分及高斯定理可进一步写成
整合(3)、(5)、(6)式, 目标函数变分可写为
令(7)式中空间积分项流动物理量变分δw系数项组合为0, 则可得伴随方程
令(7)式边界积分中流动物理量变分δw的系数项组合在一起为0, 则得对应的伴随方程边界条件
剩余项即为目标函数的梯度求解公式
2.2 伴随方程
鉴于伴随方程理论推导的复杂性, 详细过程可参考文献[12], 此处仅给出最终的数学表达式。
式中,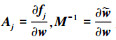 
为守恒变量与非守恒变量的变化矩阵。
式中：矢量Y中a为声速；Pr为普朗特数。
2.3 减阻优化多目标函数
为了实现飞翼布局设计点有效减阻优化, 综合考虑以下设计目标。
1) 减阻目标函数: CD2;
2) 约束升力系数目标函数: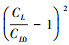 
, CL0为升力系数约束值, 用以限定升力系数CL接近约束值;
3) 约束俯仰力矩系数目标函数: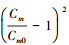 
, Cm0为俯仰力矩系数约束值, 用以限定俯仰力矩系数Cm接近约束值从而不带来较大的纵向配平损失；
4) 约束面积目标函数: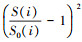 
为第i个控制剖面的面积, S0(i)为对应剖面面积的约束值, 用以限定设计剖面面积接近约束值以保证结构和内部容积;
通过加权组合方法定义如(12)式的统一目标函数
式中：CD=CDp+∫BWlinjσijdS, CDp为压差阻力；li为某一方向矢量分量；nj为物面单位方向分量；σij为黏性力张量分量(i, j=1, 2, 3);n为控制剖面的数目, Ω1, Ω2, Ω3, Ω4为各个目标函数的权值, 不优化项可以令对应的权值为0, 取值根据设计状态和各目标函数的重要性合理选取。
2.4 伴随方程边界条件
定义自由来流马赫数M∞, 压力P∞, 迎角α以及参考面积Sref, 力矩参考点(xref, yref), 易知
则升力系数、阻力系数、俯仰力矩系数中流动变量的变分为
由(12)式得, 目标函数中流动变量的变分为
根据(9)式在参考文献[12]中伴随方程边界条件的推导可知
定义: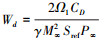 
由(20)式得方程组, 并求解伴随边界条件为
2.5 梯度方程
同理, 根据(10)式目标函数及流动控制方程中对矩阵的变分项, 即可获得梯度求解式为
3 优化设计流程与数值求解
图 1给出了优化设计流程图。
网格生成: 采用无限插值法生成结构化计算网格, 同时采用正交控制、加权平均光顺和法向量控制等措施确保网格质量。
流场数值求解: 采用Jameson的中心格式有限体积法进行空间离散, 五步Runge-Kutta显示格式时间推进, 同时加入人工黏性抑制振荡, 采用当地时间步长、隐式残值光顺、多重网格等加速收敛措施; 湍流模型采用B-L湍流模型。
伴随方程数值求解: 采用与N-S方程类似的数值解法。
设计变量及优化算法: 采用Hicks-Henne形状函数描述设计变量对物体外形变化的影响, 同时采用最速下降法进行梯度搜索。
 |
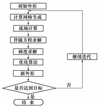图1 优化设计流程图 |
4 算例分析
4.1 算例1:某小展弦比飞翼减阻设计
设计点: Ma=0.85, α=3°, 控制剖面取机翼3个剖面, 每个剖面26个设计变量, 共78个设计变量。计算网格采用C-H网格, 如图 2所示。先后开展了2种不同约束下的优化设计。
设计1:升力、面积约束下的减阻优化设计, 根据设计状态, 限定升力系数、各剖面面积相对约束值变化不超过5%。选取目标函数中各部分的权值分别为: Ω1=120, Ω2=1, Ω3=0, Ω4=1。
表 1给出了初始与设计外形的气动特性与几何特性具体数值对比。从中看到, 初始阻力系数为0.013 1, 升力系数为0.213 7, 优化设计25步后, 阻力系数变为0.010 6, 升力系数变为0.214 3, 阻力系数下降19.5%, 而升力系数、各控制剖面面积满足约束条件。
注意到相比初始外形, 优化后带来了较大的低头力矩, 这样就会带来较大的配平损失, 从而导致实际使用升阻比降低。
设计2:为改善设计1带来的问题, 进行了升力、俯仰力矩、面积共同约束下的减阻优化设计, 对应目标函数中各部分的权值分别取: Ω1=120, Ω2=1, Ω3=0.01, Ω4=1, 保证|Cm|≤0.004。表 1为优化后具体的数值变化。迭代优化12步后, 阻力系数减小为0.010 8(与设计1保持相同量级), 下降约18.0%;升力系数变为0.206 7, 减小3.3%, 变化相对较大, 但也满足约束条件; 俯仰力矩系数由初始的0.001 8变为-0.001 6, 满足约束条件; 各控制剖面面积变化同样满足约束指标。
图 4给出了初始外形与2种约束下优化设计外形机翼展向不同站位剖面压力分布对比。可以清楚地看到2种设计外形机翼上表面的激波都被很大程度削弱, 不同之处在于有力矩约束得到的外形压力分布在50%弦长前负压值较大, 50%弦长后负压值则较小, 则对应上表面的压心靠前, 因此不会带来很大的低头力矩, 与气动力计算结果一致。
通过算例1的2种优化设计结果对比, 验证了所定义的目标函数, 推导的伴随方程边界条件及梯度求解公式是正确并有效的。
 |
图2 C-H计算网格示意图 |
 |
图3 初始外形与无/有力矩约束优化设计外形表面压力对比 |
某小展弦比飞翼不同约束条件优化前后特性对比
 |
图4 初始外形与优化外形展向不同剖面外形及压力对比 |
4.2 算例2:某大展弦比飞翼减阻设计
采用本文所发展的方法, 对某大展弦比飞翼进行跨声速状态升力、俯仰力矩和面积约束下的减阻优化设计。设计点: Ma=0.75, α=4°, 目标函数中各部分的权值分别取: Ω1=50, Ω2=2, Ω3=0.001, Ω4=0.5, 限定升力系数、各剖面面积相对约束值变化不超过5%, 俯仰力矩-0.004≤Cm≤0.008;控制剖面取机翼的4个剖面, 每个剖面26个设计变量, 加上4个剖面扭转角, 共108个设计变量。
表 2给出了优化前后气动力系数及控制剖面面积的具体数值变化。优化迭代8步, 阻力系数由初始的0.016 65减小为0.015 06, 下降约9.55%;升力系数由0.361变为0.355, 减小1.66%, 满足约束条件; 俯仰力矩系数由初始的0.006 2变为0.003 6, 满足约束条件; 各控制剖面面积变化也满足约束指标。
图 4给出了机翼展向不同站位剖面压力分布及外形对比。可以看到设计外形上表面压力负压峰值区域减小, 逆压梯度变小, 展向不同位置的激波强度都有不同程度的减弱, 尤其在展向60%~70%范围激波削弱明显。对应剖面外形的主要变化趋势是最大厚度略有减小, 且弦向位置略有后移; 扭转角主要是靠近对称面的剖面有了一个较小的正扭转角, 其余剖面变化不大。
某大展弦比飞翼优化前后气动、几何特性对比
5 结论
本文针对飞翼布局气动优化设计中的多目标多约束问题，基于伴随方法和N-S方程发展了一种气动优化设计方法，并先后进行了2种不同展弦比飞翼布局的跨声速减阻优化设计，结果表明：
1) 通过构建合理的统一目标函数形式来解决气动优化设计中的多目标多约束问题是合适的，根据伴随方法基本原理推导的伴随方程物面边界条件以及梯度求解方程是正确、有效的；
2) 所发展的设计方法在飞翼布局的多约束气动优化设计问题上，具有良好的设计效果和优化效率，因此在工程上具有广阔的应用前景。
References
- Li Weiwei. Turbomachinery aerodynamic shape optimization approach using adjoint method and its applications for blade detail design[D]. Beijing: University of Chinese Academy of Sciences, 2013 (in Chinese) [Google Scholar]
- Li Jing. The research and application of aerodynamic shape design method for high performance aircraft[D]. Xi'an: Northwestern Polytechnical University, 2014 (in Chinese) [Google Scholar]
- Xu Shengguan. A study of aerodynamic shape optimization based on Kriging surrogate models[M]. Nanjing: Nanjing University of Aerodynamics and Astronautics, 2012 (in Chinese) [Google Scholar]
- Yu Guangyuan. Aerodynamic design of large curvature diffuser channel by using adjoint method based on FFD technique[M]. Nanjing: Nanjing University of Aerodynamics and Astronautics, 2014 (in Chinese) [Google Scholar]
- Jameson A. Aerodynamic design via control theory[J]. Journal of Scientific Computing, 1988(3): 233–260 [Google Scholar]
- Kim S, Alonso J J, Jameson A. A gradient accuracy study for the adjoin-based Navier-Stokes design method[R]. AIAA-1999-16201 [Google Scholar]
- Nadarajah S, Jameson A. Studies of the continuous and discrete adjoint approaches to viscous automatic aerodynamic shape optimization[R], AIAA-2001-2530 [Google Scholar]
- Jameson A. Efficient aerodynamic shape optimization[R]. AIAA-2004-4396 [Google Scholar]
- Kim S, Alonso J J, Jameson A. Multi-element high-lift configuration design optimization using viscous continuous adjoint method[J]. Journal of Aircraft, 2004, 41(5): 1083–1096 [Google Scholar]
- Jameson A, Martinelli L, Cliff S, et al. Aerodynamic shape optimization of transonic and supersonic aircraft configurations[R]. AIAA-2005-1013 [Google Scholar]
- Lyu Z, Martins J R R A. Aerodynamic design optimization studies of a blended-wing-body aircraft[J]. Journal of Aircraft, 2014, 51(5): 1604–1617 [Article] [Google Scholar]
- Yang Xudong. Aerodynamic optimization method research based on control theory[D]. Xi'an: Northwestern Polytechnical University, 2002 (in Chinese) [Google Scholar]
- Xiong Juntao. Aerodynamic shape optimization design based on adjoint approach using Navier-Stokes equations[D]. Xi'an: Northwestern Polytechnical University, 2007 (in Chinese) [Google Scholar]
- Liu Xiaodong, Yang Xudong. Multi-point aerodynamic inverse design method of wing based on adjoint method[J]. Aeronautical Computing Technique, 2012, 42(5): 60–64 [Article] (in Chinese) [Google Scholar]
- Feng Zhenping, Li Haitao, Song Liming, et al. Aerodynamic inverse design optimization for turbine cascades based on control theory[J]. Scientia Sinca Technologica, 2013, 43(3): 257–273 [Article] (in Chinese) [Google Scholar]
- Bai Junqiang, Lei Ruiwu, Yang Tihao, et al. Progress of adjoint-based aerodynamic optimization design for large civil aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522642 [Article] (in Chinese) [Google Scholar]
- Liu Shaowei, Bai Junqiang, Yu Peixun, et al. Aerodynamic optimization design on supersonic transports considering sonic boom intensity[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 271–278 [Article] [Article] (in Chinese) [Google Scholar]
- Wang Hufeng, Bai Junqiang. Design essentials research of the flying-wing configuration[J]. Science Technology and Engineering, 2009, 9(12): 1671–1819 [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 优化设计流程图 |
| In the text | |
|
图2 C-H计算网格示意图 |
| In the text | |
|
图3 初始外形与无/有力矩约束优化设计外形表面压力对比 |
| In the text | |
|
图4 初始外形与优化外形展向不同剖面外形及压力对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.