| Issue |
JNWPU
Volume 41, Number 2, April 2023
|
|
|---|---|---|
| Page(s) | 439 - 445 | |
| DOI | https://doi.org/10.1051/jnwpu/20234120439 | |
| Published online | 07 June 2023 | |
Unified theory of integral true degrees in NM theory
NM理论中积分真度的统一理论
Mathematics and Computer Science College, Yan'an University, Yan'an 716000, China
Received:
30
June
2022
Based on the NM propositional logic system of nilpotent minimum logic, the concept of the integral truth degree of the formula is firstly proposed by integrating the function induced by the formula, and the MP rule and HS rule of the integral truth degree are proved by means of the integral invariance. Secondly, in NM propositional logic the integral similarity and integral pseudo-distance are introduced into the set of general formulas of the system, and some good properties about the similarity and pseudo-distance are proved. Finally, in terms of the concept of divergence degrees and diameter, a new membership function for reflecting the consistency degrees of theories in NM propositional fuzzy logic is proposed, which is proved that of inconsistent theories are equal to 0 and that of completely consistent theories are equal to 1.
摘要
基于在幂零极小逻辑NM(nilpotent minimun)命题逻辑系统中, 通过将公式诱导的函数进行积分的方法提出了公式的积分真度概念, 利用积分不变性证明了积分真度MP规则、HS规则; 在NM命题逻辑系统的全体公式之集上引入了积分相似度和积分伪距离, 并且证明了关于相似度和伪距离的一些性质; 通过发散度以及直径的概念, 提出了NM命题模糊逻辑中反映理论相容程度新的隶属函数, 利用隶属函数给出了相容度的概念, 证明了不相容理论的相容度为0, 完全相容理论的相容度为1。
Key words: NM propositional logic system / integral truth degree / pseudo-distance / consistency degree
关键字 : NM命题逻辑系统 / 积分真度 / 伪距离 / 相容度
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
数理逻辑的特点在于形式化而不是数值计算,为了反映程度化的思想,20世纪50年代初,Rosser教授利用“指派真值”来刻画逻辑公式和反映逻辑推理的真实程度[1],这种思想在Pavelka的系列文章[2]中得到了全面发展。后来有许多学者从不同角度提出了逻辑公式的程度化思想。
21世纪初,王国俊教授在经典二值命题逻辑中引入了命题的真度概念[3],提出了计量逻辑学理论,建立了一套近似推理模式之后,国内外学者展开了广泛的研究,得到了一些重要结果[4-6]。但是以上所有结果都建立在均匀概率测度空间上。为此,文献[7]利用赋值空间上的Borel概率测度在二值命题中引入了公式的概率真度概念。文献[8]在Łukasiewicz模糊逻辑系统Łuk、Gödel模糊逻辑系统Göd、Product模糊逻辑系统Π和R0模糊逻辑系统R0*这4种模糊命题逻辑系统中提出了公式的积分真度概念。文献[9]在一类命题逻辑系统中借助文献[7]的思想提出了利用积分定义公式真度的统一方法。文献[10-11]在SMTL命题逻辑系统中提出了公式的积分真度理论。
本文将文献[8]的思想和方法应用于NM命题逻辑系统中建立了公式积分真度的统一理论。首先,验证了积分真度MP规则、HS规则;其次,引入了积分相似度和积分伪距离;最后,引进了隶属函数和相容度的概念。值得注意的是,首先,文献[8]的结果可纳入到本文更广泛的统一框架下;其次,在NM系统中,文献[9]关于建立积分真度和相似度提出的假设条件全部成立;最后,本文的结果是对文献[10-11]的进一步推广,更加丰富了左连续三角模的模糊逻辑系统计量化研究。
1 预备知识
假设S ={p1, p2, …}是可数集, ψ是S生成的自由代数, 其中分别为¬, ∨, →一元算子和二元算子。不同的蕴含算子和赋值格决定了不同的逻辑系统, 下面介绍幂零极小逻辑NM的蕴含算子和相应的t-范数定义[12]
注1 把标准的NM代数称为[0, 1]中的NM代数, 通常取n(x)=1-x。
定义[0, 1]上的二元算子 & 和→如下
注2从ψ到R区间[0, 1]的(¬, ∨, →)型同态v: ψ→[0, 1]称为ψ的R-赋值。
定义1 幂零极小逻辑NM系统由以下12个公理模式和推理规则MP组成[13]
(NM1) (A→B)→((B→C)→(A→C))
(NM2) A & B→A
(NM3) A & B→B & A
(NM4) A∧B→A
(NM5) A∧B→B∧A
(NM6) A & (A→B)→(A∧B)
(NM7) (A→(B→C))→(A & B→C)
(NM8) (A & B→C)→(A→(B→C))
(NM9) ((A→B)→C)→(((B→A)→C)→C)
(NM10) 0→A
(NM11) ((A & B)→0)∨((A∧B)→(A & B))
(NM12) ¬¬A→A
MP规则由A, A→B推出B。
定义2 设A=A(p1, …, pn)是ψ中含有n个原子公式p1, …, pn的公式, 在A中把pi换成xi并保持¬, ∨与→不变,但把它们理解为R单位区间上相应的运算, 则得一n元函数: A(x1, …, xn): In→ I, 称是由公式A所诱导的函数[14]。
定义3 自然数列u1, u2, …叫斐波那契数列, 若u1=u2=1, 且un+un+1=un+2(n=1, 2, …)[13]。
定义4 设⊗是[0, 1]上的左连续三角模, 在[0, 1]上定义二元运算→如下[15]
则
1) →是⊗与相伴随的蕴含算子, 即a⊗b≤c当且仅当a≤b→c。
2) b→c=1当且仅当b≤c。
3) a≤b→c当且仅当b≤a→c。
4) a→(b→c)=b→(a→c)。
5) 1→c=c。
6) 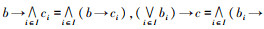 →c)。
→c)。
7) b→c关于c单调递增, 关于b单调递减。
定义5 设A=A(p1, …, pn)∈ψ, 若A(x1, …, xn)在In上几乎处处等于1, 则称A为几乎重言式[11]。
定义6 设A=A(p1, …, pn), B=B(p1, …, pn), 若A(xi, …, xn)=B(x1, …, xn)在In中几乎处处成立, 则称A与B几乎逻辑等价[11]。
2 NM理论中的积分真度
定义7 令A(p1, …, pm)为ψ中的公式, A是相应A的R函数, 那么积分
被称为A的R-真度。
定理1 设A∈ψ, 则τNM(A)=1当且仅当A是RNM-几乎重言式。
证明 若A是RNM-几乎重言式, 则τNM(A)=1, 反过来, 设A=A(p1, …, pn)∈ψ且τNM(A)=1, 则
所以A(x1, …, xn)在In几乎处处等于1, 因此A是RNM-几乎重言式。
命题1 设A∈ψ, 则τNM(¬A)=1-τNM(A)。
推论1 设A∈ψ, 则τNM(A)=0当且仅当A是RNM-几乎矛盾式。
引理1 设f(x, y)=RNM(x, y), 则f(a, c)+1≥f(a, b)+f(b, c)。
证明 设a≤c, 则f(a, c)=1。
1) 设b < a, 并且1-a>b时, f(a, b)=1-a, f(b, c)=1, 所以
设b < a, 并且1-a≤b时, f(a, b)=b, f(b, c)=1, 所以
2) 设a≤b≤c, 类似1)的证明。
3) 设c < b, 类似1)的证明。
当a>c时, 类似可证f(a, c)+1≥f(a, b)+f(b, c)成立。
综上所述, 设f(x, y)=RNM(x, y)时, f(a, c) + 1≥f(a, b)+f(b, c)成立。
定理2 设→: [0, 1]2→[0, 1]是二元函数, a, b, c∈[0, 1], I为指标集, 则
证明 由引理1可得, RNM(a, c)+1≥RNM(a, b)+RNM(b, c), 所以a→c+1≥a→b+b→c, 令a=1, 则1→c+1≥1→b+b→c, 由定义4的第5)条得, c+1≥b+b→c, 即c≥b+b→c-1。
定理3 (积分MP规则)设A, B ∈ ψ, 若τNM(A)≥α, τNM(A→B)≥β, 则τNM(B)≥α+β-1。
证明 由积分不变性定理, 不妨设A与B含有同样的原子公式p1, …, pn。由定理2得, c≥b+b→c-1, 所以B≥A+A→B-1, 从而
推论2 设A, B∈ψ, 若τNM(A)=1, τNM(A→B)=1, 则τNM(B)=1。
定理4 (积分HS规则)设A, B, C∈ψ, 若τNM(A→B)≥α, τNM(B→C)≥β, 则τNM(A→C)≥α+β-1。
证明 因为(B→C)→((A→B)→(A→C))是重言式[13], 所以由定理1得, τNM((B→C)→((A→B)→(A→C)))=1。因为τNM(B→C)≥β, 所以由定理3得, τNM((A→B)→(A→C))≥1+β-1=β, 又因为τNM(A→B)≥α, 所以再由定理3得, τNM(A→C)≥α+β-1。
推论3 设A, B, C∈ψ, 若τNM(A→B)=1, τNM(B→C)=1, 则τNM(A→C)=1。
命题2 假设In=p1∧…∧pn, Un=p1∨…∨pn, 是S中不同的原子公式, 那么
例1 计算τNM(p→q)和τNM(p→¬p∨q)的值。
解
3 NM理论中的积分相似度
定义8 设A, B∈ψ, 则称
为A与B之间的R积分相似度。
命题3 设A, B∈ψ, 则
1) ξNM(A, A)=1。
2) 当A≤B时, ξNM(A, B)=τNM(B→A); 当A>B时, ξNM(A, B)=τNM(A→B)。
3) ξNM(A, B)=ξNM(B, A)。
定理5 设A, B∈ψ, 则ξNM(A, B)=1, 当且仅当A与B几乎逻辑等价。
证明 当ξNM(A, B)=1时, 由定义6和定义8知, R(A, B)=R(B, A)=1在In几乎处处成立, 因此A与B几乎逻辑等价。反过来, 当A与B几乎逻辑等价时, A→B是重言式, B→A是重言式, 因此(A→B)∧(B→A)是重言式, 所以ξNM(A, B)=1。
引理2 设f(x, y)=RNM(x, y)∧RNM(y, x), 则f(a, c)≥f(a, b)+f(b, c)-1。
证明
1) 设a≤c, 并且1-c>a时, f(a, c)=1-c;
2) 设a≤c, 并且1-c≤a时, f(a, c)=a。
先讨论第1)种情况
① 设b < a, 并且1-a>b时, f(a, b)=1-a, f(b, c)=1-c, 所以f(a, b)+f(b, c)=2-a-c, 因此f(a, c)≥f(a, b)+f(b, c)-1。
设b < a, 并且1-a≤b时, f(a, b)=b, f(b, c)=1-c, 所以f(a, b)+f(b, c)=1-c+b, 因为b < c, 所以b-c < 0, 因此f(a, c)≥f(a, b)+f(b, c)-1。
② 设a≤b≤c, 类似于①的证明。
③ 设c < b, 类似于①的证明。
④ 对于第2)种情况以及a>c时, 类似可证f(a, c)≥f(a, b)+f(b, c)-1成立。
综上所述, 设f(x, y)=RNM(x, y)∧RNM(y, x)时, f(a, c)≥f(a, b)+f(b, c)-1成立。
定理6 设A, B, C∈ψ, 若ξNM(A, B)≥α, ξNM(B, C)≥β, 则ξNM(A, C)≥α+β-1。
证明 由引理2可得,
4 NM理论中的积分伪距离
定义9 设A, B∈ψ, 规定
定理7 ρNM: ψ×ψ→[0, 1]是ψ上的积分伪距离。设A, B, C∈ψ, 则
1) ρNM(A, A)=0。
2) ρNM(A, B)=ρNM(B, A)。
3) ξNM(A, C)≥ξNM(A, B)+ξNM(B, C)-1。
命题4 设A, B∈ψ, 当A为定理时,
5 NM理论中的积分相容度
王国俊在Łukasiewicz模糊命题逻辑系统Łuk有限理论Γ的情况下给出了相容度的定义[16], 周湘楠在Łukasiewicz模糊逻辑系统Łuk、Gödel模糊逻辑系统Göd、Product模糊逻辑系统Π和R0模糊逻辑系统R0*无限理论Γ的情况下给出了相容度的定义[17], 周红军对上述给出的2个相容度进行了补充[18]。本节将在NM命题模糊逻辑无限理论Γ的情况下给出相容度的定义。
定义10 设A∈ψ, Γ⊆ψ, 从Γ到A的准推理是一个有限序列A1, …, An, 其中An=A, 且对每个i≤n, Ai∈T∪Γ, 或者有j, k < i使Ai是由Aj与Ak运用MP规则或HS规则而得的结果, A叫做Γ的n级准推论, 记作(q)Γ(n), ├A0Γ的全体n级准推论之集记作(q)Ded(Γ(n)), 或简记作D(Γ(n))[14]。
命题5 设A∈ψ, Γ⊆ψ, A∈D(Γ(n)), 如果对每个B∈Γ均有τNM(B)≥α, 则
式中,un是斐波那契数列的第n项。
证明 证明过程类似文献[14]中的证明, 在此不再重复。
注3 由(9)式可以看出, 当Γ中各公式的真度小于1时, 则随着推演长度的增加, 所得准推论的真度将减小。
定义11 设Γ⊆ψ, 令D(Γ)={A∈ ψ丨(q)Γ├A}, 即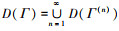 [14]。
[14]。
定义12 假设A, B∈ψ, 那么
称div(Γ)为理论Γ的发散度。当div(Γ)=1时称Γ为全发散理论。
定义13 假设Σ是ψ中的非空子集, 那么
被称为Σ的直径。
注4 1) 如果Σ是ψ包含一个定理的有限子集, 那么
定理8 设A, B是NM中的公式, Γ是NM中的理论, d(Γ(n))-d(Γ(b))=1(A∈D(Γ(n)), B∈D(Γ(b)), b是常数, A的推演长度为n, B的推演长度为b)当且仅当A是矛盾式B是重言式。
证明 假设d(Γ(n))-d(Γ(b))=1, 根据(12)式及真度的取值范围知, 0≤d(Γ(b))≤1, 0≤d(Γ(n))≤1。当d(Γ(n))-d(Γ(b))=1时, 只有当d(Γ(n))=1, d(Γ(b))=0时等式成立, 所以τNM(A)=0, τNM(B)=1, 即A是矛盾式B是重言式。
假设A是矛盾式B是重言式, 所以τNM(A)=0, τNM(B)=1, 由(12)式得, d(Γ(n))=1-τNM(A)=1, d(Γ(b)) =1 - τNM(B) =0, 所以d(Γ(b)) - d(Γ(n))=1。
定义14 假设A, B是NM中的公式, Γ是NM中的理论, 定义
并且
称i(Γ)为NM中理论Γ的极性指标。
定义15 假设Γ是NM中的理论, 那么
称ζ(Γ)为NM中理论Γ的相容度。(i(Γ)是由上述定义14给出)。
定理9 在NM中存在一系列相容理论Γ1, Γ2, …, Γk序列, 它们的发散度为div(Γk)= 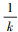 (k=1, 2, …)。
(k=1, 2, …)。
证明 假设A1=p2, Ak=p1→Ak-1(k=2, 3, …), p1, p2是不同的原子公式, 并且(v(p1)=x1, v(p2)=x2),根据(2)~(3)式得
所以
令Γk={Ak}, 因此Akn ∈D(Γk), 下面证明Γk是相容理论, 证明过程可参考文献[17]。
取B=p1→p1∈D(Γk)并且B(x1)≡1, 因为Akn+1=Akn⊗ ≤Akn, ρNM(B, Akn)随着n的增加而增加, 因此div(Γk)= 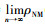 (B, Akn)。根据(8)式得, ρNM(B, Akn)=1-τNM(Akn)。根据(4)式得
(B, Akn)。根据(8)式得, ρNM(B, Akn)=1-τNM(Akn)。根据(4)式得
因此
所以
定理10 假设Γ是NM中的理论, 那么
1) Γ是相容的当且仅当i(Γ)=1。
2) Γ是不相容的当且仅当i(Γ)=0。
证明 假设Γ是不相容的, 那么Γ├C(C是矛盾式), 因此C∈d(Γn)∈D(Γ)。因为每个理论都包含定理, 所以A∈d(Γb)∈D(Γ)(A是重言式)。因此得, d(Γ(n))-d(Γ(b))=1, 所以i(Γ)=0。另一方面, 假设i(Γ)=0显然成立, 因此(2)式成立,(1)式自然也成立。
定理11 假设Γ是NM中的理论, 那么
1) 如果i(Γ)=0, 则div(Γ)=1, 但反之不成立。
2) 如果div(Γ) < 1, 则i(Γ)=1, 但反之不成立。
证明 假设i(Γ)=0, 根据定理10得, Γ是不相容的, 根据(10)~(12)式知, div(Γ)=sup{pNM(A, B)}=1。另一方面, 假设div(Γ)=1, 即理论Γ是完全发散的, 但不能推出Γ是不相容的, 即i(Γ)=0, 令Γ=S是由所有原子公式构成的, 见文献[18],知Γ=S是完全发散并且是相容理论。根据定理10知, 当理论Γ是相容时, i(Γ)=1, 因此div(Γ)=1不能推出i(Γ)=0。因此(1)式成立, (2)式自然也成立。
定理12 假设Γ是NM中的理论, 那么
1) Γ是完全相容的, 当且仅当ζ(Γ)=1。
2) Γ是不相容的, 当且仅当ζ(Γ)=0。
3) Γ是相容的, 当且仅当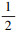 ≤ζ(Γ)≤1。Γ是相容且全发散当且仅当ζ(Γ)=
≤ζ(Γ)≤1。Γ是相容且全发散当且仅当ζ(Γ)= 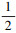 。
。
证明
1) 假设Γ是完全相容的, 显然成立。假设ζ(Γ)=1, , 如果Γ不是完全相容的, 那么Γ就有2种情况, 第一种情况是Γ是相容的, 那么div(Γ)≠0, 由定理10的第1)条知, i(Γ)=1, 所以由(16)式知, ζ(Γ) < 1, 另一种情况类似可证明成立。
2) 假设Γ是不相容的, 显然成立。假设ζ(Γ)=0, 则由(16)式和div(Γ)≤1知, i(Γ)≤0, 因为i(Γ)∈{0, 1}, 因此i(Γ)=0, 由定理10的第2)条知, Γ是不相容的, 因此(2)式成立。
3) 假设Γ是相容的, 那么div(Γ)≠0, 由定理10的第1)条及(16)式知, ζ(Γ)=1- 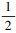 div(Γ)ζ(Γ)≥
div(Γ)ζ(Γ)≥ 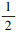 , 又因为ζ(Γ)∈[0, 1], 因此
, 又因为ζ(Γ)∈[0, 1], 因此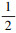 ≤ζ(Γ)≤1。假设
≤ζ(Γ)≤1。假设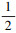 ≤ζ(Γ)≤1, 如果Γ不相容, 那么div(Γ)=1, 由定理10的第2)条及(16)式知ζ(Γ)=0, 与
≤ζ(Γ)≤1, 如果Γ不相容, 那么div(Γ)=1, 由定理10的第2)条及(16)式知ζ(Γ)=0, 与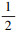 ≤ζ(Γ)≤1矛盾, 所以当
≤ζ(Γ)≤1矛盾, 所以当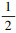 ≤ζ(Γ)≤1, Γ是相容的。对于后半部分显然成立。
≤ζ(Γ)≤1, Γ是相容的。对于后半部分显然成立。
例2 假设Γ是NM中的理论, 现有理论Γ中的3个公式分别为A, B, C, 它们的真度分别为τNM(A)=0.6, τNM(B)=1, τNM(C)=0.7, 试比较理论Γ1={A, B}的相容度与理论Γ2={B, C}的相容度大小关系。
解 根据(4), (8), (10)式知ρNM(B, A)大于ρNM(B, C), 因此理论Γ1={A, B}的div(Γ)大于理论Γ2={B, C}的div(Γ)。因为理论Γ1={A, B}的i(Γ)小于理论Γ2={B, C}的i(Γ), 所以理论Γ1={A, B}的div(Γ) 1- 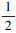 (i(Γ)) 大于理论Γ2={B, C}的div(Γ) 1-
(i(Γ)) 大于理论Γ2={B, C}的div(Γ) 1- 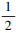 (i(Γ)), 因此理论Γ1={A, B}的相容度小于理论Γ2={B, C}的相容度。
(i(Γ)), 因此理论Γ1={A, B}的相容度小于理论Γ2={B, C}的相容度。
注5 例2的结果验证了定义的相容度具有合理性。
6 结论
本文在NM系统中首先引进了积分真度的概念,验证了积分真度MP规则、HS规则,其次利用积分真度的概念引进了积分相似度和积分伪距离的概念,并验证了它们之间的一些性质,最后引进了极性指标与相容度的概念,验证了完全相容理论的相容度为1,不相容理论的相容度为0。
References
- ROSSER J B, TURQUETTE A R. Many-valued logic[M]. Amsterdamm: North-Holland, 1952: 46–66 [Google Scholar]
- PAVELKA J. On fuzzy logic Ⅰ, Ⅱ, Ⅲ[J]. Zeitschr f Math Logic and Grundlagen d Math, 1979, 25(1): 45–52 [CrossRef] [Google Scholar]
- WANG Guojun, FU Li, SONG Jianshe. Theory of truth degrees of propositions in two-valued logic[J]. Science in China(Series A), 2002, 45(9): 1106–1116 [Google Scholar]
- WANG Guojun, SONG Jianshe. Graded method in propositional logic[J]. Acta Electronica Sinica, 2006, 34(2): 252–257. [Article] (in Chinesse [Google Scholar]
- HUI Xiaojing. Quantification of truth-based SBL-~axomatic expansion systems[J]. Science in China: Information Science, 2014, 44(7): 900–911. [Article] (in Chinese) [Google Scholar]
- WANG Guojun, SHE Yehong. Topological description of divergency and consistency of two-valuedpropositionaltheories[J]. Acta Mathematical Sinica, Chinese Series, 2007, 50(4): 841–850 [Google Scholar]
- ZHOU Hongjun. Borel probabilistic and quantitative logic[J]. Science China Information Science, 2010, 53(2): 1–12 [NASA ADS] [CrossRef] [Google Scholar]
- WANG Guojun, LEUNG Y. Integrated semantics and logic metricspaces[J]. Fuzzy Sets and Systems, 2003, 136(4): 71–91 [CrossRef] [Google Scholar]
- WANG Guojun. A unified integrated method for evaluating goodness of propositions in several propositional logic systems and its applications[J]. Chinese Journal of Electronics, 2012, 21(2): 195–201 [Google Scholar]
- LI Jun, DENG Fuxi. Unified theory of truth degrees in n-valued S-MTL propositional logic[J]. Acta Electronica Sinica, 2011, 39(8): 1864–1868 (in Chinese) [Google Scholar]
- LI Jun, YAO Jintao. Integral truth degree theory of formulas in propositional logic system SMTL[J]. Journal of Electronics, 2013, 41(5): 878–883. [Article] (in Chinese) [Google Scholar]
- ESTEVA F, GODO L. Monoidal t-norm based logic: towards a logic for left-continuous t-normas[J]. Fuzzy Sets and Systems, 2001, 124(4): 271–288 [Google Scholar]
- PEI Daowu. Fuzzy logic theory based on triangle mode and its application[M]. Beijing: Science Press, 2013 (in Chinese) [Google Scholar]
- WANG Guojun. Non-classical mathematical logic and approximate reasoning[M]. Beijing: Science Press, 2008 (in Chinese) [Google Scholar]
- WANG Guojun. Introduction to mathematical logical and resolution principle[M]. 2nd ed. Beijing: Science Press, 2006 (in Chinese) [Google Scholar]
- WANG Guojun, ZHANG Wenxiu. Consistency degrees of finite theories in Lukasiewicz propositional fuzzy logic[J]. Fuzzy Sets and Systems, 2005, 149(2): 275–284 [Google Scholar]
- ZHOU Xiangnan, WANG Guojun. Consistency degrees of theories in some systems of propositional fuzzy logic[J]. Fuzzy Sets and Systems, 2005, 152(2): 321–331 [Google Scholar]
- ZHOU Hongjun, WANG Guojun. A new theory consistency index based on deduction theorems in several logic sysstem[J]. Fuzzy Sets and Systems, 2006, 157(3): 327–443 [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


