| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 377 - 385 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230377 | |
| Published online | 01 October 2024 | |
Deck motion prediction using neural kernel network Gaussian process regression
基于神经核网络高斯过程回归的甲板运动预测
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
Received:
10
June
2023
Deck motion prediction and compensation are critical technologies for carrier-based aircraft automatic landing. Traditional deck motion prediction methods rely on precision of motion models and parameter adjustments, facing challenges in adaptability to complex sea conditions, different types of carriers, changes in flight conditions, and limitations in prediction duration, as well as reliability issues. This paper proposes a deck motion prediction method based on the neural kernel network Gaussian process regression (NKN-GPR) model. The NKN-GPR model can utilize a neural kernel network (NKN) to automatically construct the Gaussian process regression (GPR) model′s composite kernel, effectively addressing the limitations of the automated kernel search (ACKS) algorithm, which heavily depends on manual prior knowledge. Simulation data is generated using a combination of sine wave and power spectrum models, and the NKN-GPR model is compared with an autoregressive (AR) model based on least squares in a simulated validation. The simulation results demonstrate that the NKN-GPR model exhibits significant advantages in motion prediction accuracy, smoothness, and prediction duration, which confirms the effectiveness of the proposed algorithm. This study provides theoretical support for safe automatic landing of carrier-based aircraft.
摘要
甲板运动预测与补偿是舰载机自动着舰的关键技术之一。传统甲板运动预测方法依赖于运动建模的准确性和参数调整，面临复杂海况、不同舰型、航态变化时具有适应性差、预测时长短、结果可靠性低等问题。提出一种基于神经核网络高斯过程回归(NKN-GPR)的甲板运动预测模型，使用神经核网络(NKN)实现高斯过程回归(GPR)模型自动复合核构造，有效改善基于规则库自动核搜索(ACKS)算法依赖人工先验知识的不足。以正弦波组合模型和功率谱模型构造仿真数据，对NKN-GPR模型和基于最小二乘法的自回归(AR)模型进行对比仿真验证，仿真结果表明，NKN-GPR模型在运动预测精度、平滑性、预测时长等方面具有显著优势，证明了所提算法的有效性，可为舰载机自动安全着舰提供理论支撑。
Key words: automatic carrier landing / deck motion prediction / Gaussian process regression / neural kernel networks / automatic composite kernel construction
关键字 : 自动着舰 / 甲板运动预测 / 高斯过程回归 / 神经核网络 / 自动复合核构造
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
舰船海上航行会因海浪、海涌和风力的影响产生纵向运动(纵荡、沉浮、俯仰)和横侧向运动(横荡、横滚、偏航)，导致甲板上的着舰点做三自由度漂移。舰载机着舰接近舰尾时，要求飞机和甲板的运动保持高度同步，将纵向偏差限制在小范围阈值内，以避免着舰挂索过程中飞机意外逃逸、撞击甲板等事故发生。但由于机、舰之间指令解算和信号传输存在时延，舰载机对引导控制指令的响应存在滞后性，致使同步运动十分困难[1]。因此，使用甲板运动预测补偿引导控制指令，是实现舰载机自动着舰的重要手段，也是当前研究的热点问题。
甲板运动预测方法采用的模型一般可分为舰船流体动力学模型、经典时间序列模型、机器学习模型和混合模型[2]。早期甲板运动预测基于舰船流体动力学模型，将艏前波高测量值应用于卷积方程，进而获取舰船甲板运动的预测，其性能取决于舰船响应核函数[3]。但实际应用时难以获得高精度物理模型，导致适应性较差、预测精度较低。为克服需要精确估计响应核函数、噪声和状态空间的缺陷，基于经典时间序列模型的运动预测方法得到广泛研究。根据输入的波浪传感器时间序列和舰船响应数据，使用时间序列模型预测舰船实时运动，如基于统计学的自回归(AR)模型、自回归移动平均模型等[4–5]。经典时间序列模型采用的统计学方法具有计算量小、实时性好的优点，但是难以处理噪声数据，缺乏对环境的适应性。
机器学习为甲板运动预测问题提供了新的解决思路。基于奇异值分解和遗传算法的神经网络、支持向量机、径向基函数神经网络、长短期记忆神经网络等机器学习方法在海试中被证明能够准确预测波浪序列引起的舰船运动响应[6–9]。但以上方法通常只针对特定工况有较好的预测性能，当面对新的工况或随机性过强时，训练模型的适应性差。为解决这一问题，基于机器学习方法的混合模型预测成为近年研究的热点。结合预测模型与预处理技术，能克服单一机器学习模型预测的缺点。Xu等[10]将移动网格搜索-最小平方支持向量机的混合模型用于在线预测波浪中的舰船滚动运动。Skulstad等[11]建立动态模型和神经网络组成的合作性混合模型，其中神经网络用于预测动态模型的加速度误差，以实现预测精度提升。此外，相关研究还提出了自适应动态粒子群优化算法、双向长短时记忆神经网络、长短时记忆网络-高斯过程回归、EMD-SVR等各类混合模型[12–14]。与传统单一机器学习预测方法相比，混合模型具有更好的预测精度，但很少考虑预测结果的不确定性，且存在模型复杂、参数难以调整、泛化性差、不易在线应用的缺点。
另一方面，虽然预测精度是甲板运动预测研究中的重要指标，但获取强随机性下舰船运动的趋势和可靠地预测不确定性信息更有利于提高舰载机自动着舰的安全性和效率。高斯过程回归(GPR)是近年发展起来的一种概率机器学习方法，有严格的统计学习理论支撑，对高维、小样本、非线性等复杂问题具有高适应性、强泛化能力、易于计算模型预测的置信区间[15]，如余敏等[16]采用稀疏伪输入高斯过程回归方法进行空间自由翻滚目标的运动预测，为机器人抓捕提供了前提条件。但传统高斯过程回归通常需要给定核函数的参数化形式，选择合适的核函数是GPR建模的关键挑战。Duvenaud等[17]在传统GPR模型框架下嵌入一种自动复合核搜索(ACKS)算法，能够自动捕获数据内在结构特性，充分挖掘数据中隐含的模式信息，从而建立更精准的回归模型，实现了观测数据到预测数据端到端自动模型构造及预测。基于ACKS的高斯过程在锂电池剩余寿命估计、导弹气动性能评价等复杂问题中展现出显著优势，明显提升了GPR模型的性能[18–19]。但ACKS的主要缺点是基于规则库的离散搜索内核语法非常昂贵，即使对于短时间序列也常需要数小时的学习计算。Sun等[20]在上述ACKS基础上提出了神经核网络(NKN)方法，用神经网络形式代替基于规则库的离散内核搜索语法，实现了复合核函数快速构造。本文将神经核网络高斯过程回归(NKN-GPR)方法应用于甲板运动预测，能根据采集的甲板运动数据自动地快速构建模型，预测结果平滑性高、泛化性强，避免其他机器学习模型或混合模型参数难调、易过拟合等缺点。面对强随机性下的甲板运动数据，仍能够获得精确的预测结果，计算可靠的预测置信区间及甲板运动趋势，有利于提高舰载机自动着舰的安全性和效率。
1 问题描述
舰船纵向(纵荡、沉浮、俯仰)和横侧向运动(横荡、横滚、偏航)间耦合作用很小, 可视为彼此独立的过程[21]。舰船甲板运动预测是根据历史观测数据y=[yt, yt-1, …, yt-T+1]实现未来时刻运动状态估计的过程。其中, (t-T+1)~t表示观测数据的时间窗口, T表示窗口内采集的数据点数目, yt为t时刻描述甲板单自由度运动状态的标量值, 整合时间和状态序列可得如下历史观测数据集
甲板运动预测的目标是根据数据集D估计未来时刻t*∈(t~t+M)的运动状态f(t*)。其中, M为前向预测时间窗口的大小, 是衡量预测能力的重要指标; f(·)表示运动预测器, 使用GPR实现, 并基于NKN实现GPR复合核函数的自动构造。
2 高斯过程回归
GPR是使用高斯过程先验对数据进行回归分析的非参数概率模型[22], 能够拟合非线性数据, 给出预测样本的完整后验分布, 提供模型关于预测的置信区间, 具有良好的模型可解释性。本节简要阐述GPR模型框架及训练过程。
2.1 模型框架
高斯过程(GP)是任意有限个随机变量具有联合高斯分布的集合, 其性质完全由均值函数m(x)和协方差函数k(x, x′)确定, 其中x, x′∈Rd为任意随机变量。GP可定义为
通常可对数据进行预处理使均值函数为0。
给定训练集样本D=(X, y)=({xi}, {yi})i=1n, 其中X表示n个输入向量xi组成的特征矩阵, y表示n个标量观测值yi组成的观测向量, 考虑以下一般的线性回归模型
式中：yi为在xi处的观测值；f(·)为函数值；xi为输入向量；εi~N(0, σn2)为独立同分布的高斯噪声, 可得观测值y的先验分布为
观测值y和预测值f*的联合先验分布为
式中：K(X, X)=(kij)为n×n对称正定协方差矩阵, 矩阵元素kij=k(xi, yj)用来度量xi和yj之间的相关性; K(X, x*)=K(x*, X)T用来度量训练样本输入X和测试点x*之间的协方差; k(x*, x*)表示测试点x*自身的方差。计算预测值f*的后验分布为
式中
则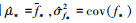
即为测试点x*对应预测值f*的均值和方差。
2.2 模型训练
GPR的协方差函数k(x, x′)称作核函数, 本质上决定了样本点相似性的度量方法。作为一种非参数模型, 当核函数、训练数据给定, GPR模型唯一确定。但核函数自身是有参数的, 通常作为GPR模型的超参数, 一般通过极大似然估计获得, 即通过最大化边际对数似然函数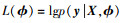
来确定核函数参数ϕ。如对于平方指数核函数
式中：l为方差尺度；σ2为信号方差, 可记核函数参数ϕ={l, σ2}。最大化L(ϕ)等价于最小化如(10)式所示的负对数似然函数
获得最优超参数ϕ后, GPR模型完全确定, 利用(7)~(8)式即可计算测试点x*对应的预测值f*及其方差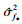
。
3 NKN自动复合核构造
GPR需要提前给定核函数k(x, x′)的参数化形式, 其泛化能力严重依赖于核函数的选择。由于舰船运动规律与舰船型号、航行状态等因素相关, 难以获得历史运动数据的结构特性, 基于单一核函数的GPR模型无法实现对未来运动状态的准确预测, 构造合理的复合核函数至关重要。本节首先介绍复合核函数常用的ACKS算法, 进一步给出基于神经核网络的改进形式和训练方法。
3.1 ACKS算法
ACKS算法的核心是定义基础核函数库和复合核函数构造规则, 即使用“加”、“乘”等基本运算操作基础SE核、Per核、Lin核、RQ核, 从而得到新的复杂核函数[23]。各基础核函数定义为
以上基础核函数适用于描述特殊的数据结构特性: SE核假设函数具有平滑变化结构; Per核假设函数具有重复变化结构; Lin核假设函数具有线性变化结构; RQ核假设函数具有多尺度变化结构。基于“加”、“乘”等操作的复合核构造要满足(12)式所示的函数空间封闭性
式中：k1表示当前核函数中的任意组件；k2表示任意类型的基础核。基于以上构造规则, 传统ACKS算法可使用启发式算法搜索更优的复合核函数。但基于规则库的离散搜索内核语法非常昂贵, 很难应用于对学习时间要求短的甲板运动预测。NKN与传统ACKS算法在基础核库和构造规则方面类似, 但采用神经网络代替基于构造语法的离散搜索, 能够有效提高复合核的构造效率。
3.2 NKN结构
NKN仍满足(12)式所要求的“加”、“乘”操作的封闭性, 给定x1, x2∈Rd作为NKN的输入, 输出复合核函数k(x1, x2)∈R(或C)。NKN的结构与神经网络类似, 第一层由基础核函数组成, 随后的模块为线性层和乘积层交替排列, 以通过“加”、“乘”运算将基础核组合成复合核, 如图 1所示。
基础核层：基础核函数可使用任何核函数, 每个基础核函数都有对应的超参数, 与神经核网络中的其他参数一同被优化。
线性层：类似深度神经网络中的全连接层, 每一层hl=Wlhl-1表示前一层的非负线性组合。线性层实现核函数单元的“加”运算, 可灵活地捕获到数据中隐含的复杂结构信息, 如Lin核“加”Per核表示数据具有趋势周期变化结构。
乘积层：NKN采用固定连接模式的乘积层, 每个单元是上一层多个单元的乘积。乘积层可实现核函数单元的“乘”运算, 该运算允许考虑核函数中不同维度输入对输出值的非线性影响, 或不同结构核函数对输出值的非线性影响, 即核函数对模型可能存在相似性的影响。
激活函数：NKN每层可包含一个非线性激活函数, 但需要保证核运算的封闭性, 可以选择具有正系数的多项式或者指数函数f(z)=ez等。
 |
图1 NKN结构图 |
3.3 NKN训练
NKN中所有可训练的参数可分组为2类: 基础核函数中的超参数, 如SE核中的长度尺度; 线性层的参数, 即线性组合的权重值。可通过最大化边际似然L(ϕ)联合学习上述参数。由于NKN架构是可微的, 可使用基于梯度的优化方法优化所有参数。
3.4 NKN-GPR甲板运动预测流程
NKN-GPR应用于甲板运动预测的流程大致分为初始化、训练和预测3个阶段。初始化阶段, 根据甲板运动数据的复杂性设定NKN基础核层核函数类型、副本数量、超参数初始值、最大迭代次数等。训练阶段, 根据各维度甲板运动周期特点设定采样频率, 将采样数据用于训练NKN-GPR模型参数。通过最大化边际似然L(ϕ)联合学习NKN中所有可训练的参数。训练参数不断迭代优化, 直至达到最大迭代次数或停止条件。预测阶段, 将外推时间序列作为输入数据, 实现甲板运动的多步前向预测。
NKN构造核函数的计算复杂度为O(N2m), 其中, N为数据点数量, m为网络层数。在此计算复杂度下, 可根据甲板运动数据的变化快速重建复合核函数。在此基础上, 运动预测的计算量主要在于核函数矩阵求逆, 计算复杂度为O(N3)。因此, 基于NKN-GPR的甲板运动预测与传统GPR具有相近的计算成本。同时, 与其他机器学习和复杂的混合预测模型相比, NKN-GPR需要优化的参数数量更少, 模型易于收敛, 具有更好的泛化性。
4 仿真校验
4.1 实验模型设置
甲板运动可分为纵向运动和横侧向运动, 纵向运动对理想着舰点产生的影响较大, 作为本节的仿真对象。参考美国F/A-18舰载机着舰过程, 飞机着舰前12.5 s需要将理想着舰点垂直运动的位置预测结果补偿到飞控系统。理想着舰点的垂直运动位置信号HDM由(13)式给出
式中：LTD为舰体俯仰中心至着舰点的距离；HV为甲板的纵向沉浮运动；θV为甲板的俯仰运动。
实际应用中常用基于正弦波组合的甲板运动确定性模型和基于功率谱的甲板运动随机性模型。基于正弦波组合的甲板运动模型用多个正弦函数叠加来描述甲板运动。文献[24]给出了航母以30 kn速度航行时, 海浪及海风作用下舰体运动公式
基于功率谱的甲板运动模型是白噪声通过与功率谱相对应的成型滤波器得到的频域运动函数。文献[25]给出了美国ESSEX级航母在8 kn航速、航向左舷60°、浪高5.18 m且海况主要为浪涌时的沉浮与俯仰运动公式
式中
本文在正弦波组合模型产生的沉浮和俯仰运动数据基础上, 添加高斯噪声数据, 作为用于运动预测的仿真数据。同样地, 选取基于功率谱模型产生的沉浮运动数据。由舰体运动特征频率可知理想着舰点垂直运动周期为6~13 s, 预测器观测数据的采样时间选为0.5 s。
仿真中使用Lin、SE、RQ和Per核4种基本核, 经过NKN的线性层和乘积层构造出新的核函数, 来描述2个数据点x1和x2之间关系。为提高模型的预测能力, NKN第一层基本核的数量可为多个。线性层和乘积层交替进行, 且乘积层使上一层的核数量减半。用LinearP表示经过加法层得到的P个核函数, 用ProductQ表示经过乘积层得到的Q个核函数, 当第一层每种基本核数量为2和4个时, 各层作用后对应核函数分别表示为Linear16-Product8-Linear8-Product4-Linear1和Linear16-Product8-Linear8-Product4-Linear4-Product2-Linear1, 如图 1所示。
为验证NKN方法的有效性, 给出基于AR模型的对比结果。其中, AR模型的参数估计使用最小二乘法。对仿真结果, 使用误差绝对值指标对每一步预测结果进行评估, 使用误差平方和对整体预测及趋势进行评估, 使用均方误差(EMS)和均方根误差(ERMS)对预测模型的整体精度进行评估, 计算公式为
式中：yi为运动模型(14)式或(15)式产生的结果, 不加噪声作为真实值; fi为模型的输出结果。作为运动的预测值, EMS和ERMS的值越小, 表明运动预测的结果越准确。
4.2 正弦波组合模型数据仿真与分析
针对正弦波组合的甲板沉浮运动模型，分别采用NKN-GPR和最小二乘法进行预测，最小二乘法阶数为30。具体地，利用前50 s历史运动数据，预测未来3 s(6步)的运动，总预测时间为25 s。运动数据采集存在均值为0，方差为0.1的高斯噪声。NKN第一层各个基础核数量为2，经线性层和乘积层作用后各层的核函数为Linear8-Product4-Linear4-Product2-Linear1。算法的对比仿真实验结果如图 2~5所示。
NKN-GPR预测误差绝对值最大为0.42，均方误差为0.044，均方根误差为0.21；最小二乘法预测的误差绝对值最大为0.95，均方误差为0.21，均方根误差为0.46。整体来看，NKN-GPR预测精度提高54%，预测误差更小，外推预测拟合度更高。另一方面，如图 6所示，NKN-GPR预测结果更为平滑，能够更好地反映出甲板运动数据的趋势、周期性等属性。
针对正弦波组合的甲板俯仰运动模型，分别采用NKN-GPR和最小二乘法进行预测。由于俯仰运动周期较长，因此利用75 s的历史运动数据，预估未来3 s(6步)的运动，总预测时间为25 s。噪声添加及NKN结构与沉浮运动预测采用相同设置，最小二乘法阶数为55。对比仿真结果如图 7~10所示。
仿真结果显示，NKN-GPR预测误差的绝对值最大为0.20，均方误差为0.01，均方根误差为0.10；与之对应，最小二乘法预测误差的绝对值最大为0.24，均方误差为0.01，均方根误差为0.11。整体来看，NKN-GPR预测精度提高9%，预测误差更小，外推预测拟合度更高。同时NKN-GPR预测更加平滑，能够更好地反映出甲板运动数据的趋势、周期性等属性。
NKN-GPR在预测时长上具有明显优势。仍然针对正弦波组合的甲板沉浮运动模型式，分别采用NKN-GPR和最小二乘法进行较长时间预测。具体地，利用50 s的历史运动数据，预测5 s(10步)的运动，总预测时间为25 s。噪声添加及NKN结构同上，最小二乘法阶数为30。对比仿真结果如图 11~12所示。
根据仿真结果，采用最小二乘法已不能进行有效预测，而NKN-GPR则不受预测时长影响，仍能够准确反映出甲板运动数据的趋势、周期性等，实现长时间外推预测。NKN-GPR具有预测时长的明显优势，可以通过对历史数据的快速学习建模，做出长时间准确的预测。对于甲板运动预测，长时间的预测更加有利于预测理想着舰点位置，提升舰载机着舰的成功率和安全性。
 |
图2 甲板沉浮运动预测对比图 |
 |
图3 甲板沉浮运动预测误差绝对值 |
 |
图4 甲板沉浮运动预测误差平方值 |
 |
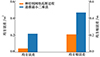图5 甲板沉浮运动预测均方误差和均方根误差 |
 |
图6 甲板沉浮运动预测局部放大图 |
 |
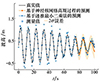图7 甲板俯仰运动预测对比图 |
 |
图8 甲板俯仰运动预测误差绝对值 |
 |
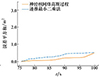图9 甲板俯仰运动预测误差平方值 |
 |
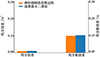图10 甲板俯仰运动预测均方误差和均方根误差 |
 |
图11 甲板沉浮运动预测(5 s)对比图 |
 |
图12 甲板沉浮运动预测(5 s)误差绝对值 |
4.3 功率谱模型数据实验及分析
针对功率谱模型的甲板沉浮运动模型，分别采用NKN-GPR和最小二乘法进行预测。具体地，利用50 s历史运动数据，预测3 s(6步)的运动，总预测时间为25 s。由于功率谱模型产生的仿真数据结构比较复杂，设定基础核各为4个，层数排序为Linear16-Product8-Linear8-Product4-Linear4-Product2-Linear1，最小二乘法阶数为8。由于基于功率谱模型的甲板运动数据结构复杂，NKN-GPR采用迭代方式进行预测，即根据数据变化特性，按照一定时长，基于新的观测数据，建立新的学习模型并进行预测。对比仿真结果如图 13~16所示。
仿真结果显示，NKN-GPR预测的误差绝对值最大为0.80 m，均方误差为0.18 m2，均方根误差为0.42 m，而最小二乘法已无法实现有效预测。基于功率谱模型的甲板运动预测难度较大，NKN-GPR在预测过程中虽然有一定的相位滞后，但是仍然能够较准确地反映出数据的部分递减及周期属性。
 |
图13 甲板沉浮运动预测对比图 |
 |
图14 甲板沉浮运动预测误差绝对值 |
 |
图15 甲板沉浮运动预测误差平方值 |
 |
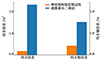图16 甲板沉浮运动预测均方误差和均方根误差 |
5 结论
针对传统甲板运动预测方法的局限，本文使用概率机器学习中的NKN-GPR模型对甲板运动预测进行研究，研究结论如下：
1) 对比AR模型中的最小二乘法，2种工程模型下的3种代表性甲板运动仿真结果均表明NKN-GPR模型预测精度高，在正弦波组合甲板沉浮和俯仰运动上预测精度分别提高54%, 9%，且预测结果平滑，能准确反映观测数据的结构属性，直接给出预测置信区间；
2) 将神经网络形式的结构运用于GPR的复合核自动搜索，能够快速地构造出适合数据特性的核结构，准确捕获隐含的内在数据结构特性，实现观测数据到预测结果端到端自动生成，不需依赖人工先验经验；
3) NKN-GPR通过对历史观测数据学习进行快速预测，提高了甲板运动预测的精度和时长，预测时长超过5 s，为舰载机自动安全着舰提供了有效理论支撑。
References
- ZHU Qidan, ZHANG Zhi, ZHANG Wen. Aircraft carrier aircraft safe takeoff and landing technology[M]. Harbin: Harbin Engineering University Press, 2016 (in Chinese) [Google Scholar]
- SUN Q, TANG Z, GAO J P, ZHANG G C. Short-term ship motion attitude prediction based on LSTM and GPR[J]. Applied Ocean Research, 2022, 118: 102927 [Article] [CrossRef] [Google Scholar]
- KAPLAN P. A study of prediction techniques for aircraft carrier motions at sea[C]//AIAA 6th Aerospace Sciences Meeting, 1968: 68–123 [Google Scholar]
- YUMORI I. Real time prediction of ship response to ocean waves using time series analysis[C]//Proceedings of OCEANS 81, 1981: 1082–1089 [Google Scholar]
- JIANG H, DUAN S L, HUANG L, et al. Scale effects in AR model real-time ship motion prediction[J]. Ocean Engineering, 2020, 203: 107202 [Article] [CrossRef] [Google Scholar]
- KHAN A, BIL C, MARION K E. Ship motion prediction for launch and recovery of air vehicles[C]//Proceedings of OCEANS 2005 MTS/IEEE, 2005: 2795–2801 [Google Scholar]
- LUO W, REN J. On the identification of coupled pitch and heave motions using support vector machine[C]//2016 Chinese Control and Decision Conference, 2016: 3316–3321 [Google Scholar]
- YIN J, ZOU Z, XU F. On-line prediction of ship roll motion during maneuvering using sequential learning RBF neural networks[J]. Ocean Engineering, 2013, 61, 139–147 [Article] [CrossRef] [Google Scholar]
- SILVA K M, MAKI K J. Data-driven system identification of 6-DoF ship motion in waves with neural networks[J]. Applied Ocean Research, 2022, 125: 103222 [Article] [CrossRef] [Google Scholar]
- XU C Z, ZOU Z J. Online prediction of ship roll motion in waves based on auto-moving gird search-least square support vector machine[J]. Mathematical Problems in Engineering, 2021, 2021, 2760517 [Google Scholar]
- SKULSTAD R, LI G, FOSSEN T, et al. A cooperative hybrid model for ship motion prediction[J]. Modeling Identification and Control, 2021, 42(1): 17–26 [Article] [CrossRef] [Google Scholar]
- ZHANG Biao, PENG Xiuyan, GAO Jie. Ship motion attitude prediction based on ELM-EMD-LSTM integrated model[J]. Journal of Ship Mechanics, 2020, 24(11): 1413–1421 [Article] (in Chinese) [Google Scholar]
- ZHANG G, TAN F, WU Y. Ship motion attitude prediction based on an adaptive dynamic particle swarm optimization algorithm and bidirectional LSTM neural network[J]. IEEE Access, 2020, 8: 90087–90098 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- NIE Z, SHEN F, XU D, et al. An EMD-SVR model for short-term prediction of ship motion using mirror symmetry and SVR algorithms to eliminate EMD boundary effect[J]. Ocean Engineering, 2020, 217: 107927 [Article] [CrossRef] [Google Scholar]
- HE Zhikun, LIU Guangbin, ZHAO Xijing, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121–1129 [Article] (in Chinese) [Google Scholar]
- YU Min, LUO Jianjun, WANG Mingming. Real-time motion prediction of space tumbling targets based on machine learning[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(2): 195–205 [Article] (in Chinese) [Google Scholar]
- DUVENAUD D, LLOYD J, GROSSE R, et al. Structure discovery in nonparametric regression through compositional kernel search[C]//Proceedings of the 30th International Conference on Machine Learning, PMLR, 2013: 1166–1174 [Google Scholar]
- RICHARDSON R R, OSBORNE M A, HOWEY D A. Gaussian process regression for forecasting battery state of health[J]. Journal of Power Sources, 2017, 357: 209–219 [Article] [Google Scholar]
- HU Weijie, HUANG Zenghui, LIU Xuejun, et al. Missile aerodynamic performance prediction of Gaussian process through automatic kernel construction[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 289–302 [Article] (in Chinese) [Google Scholar]
- SUN S, ZHANG G, WANG C, et al. Differentiable compositional kernel learning for Gaussian processes[C]//Proceedings of the 35th International Conference on Machine Learning, PMLR, 2018: 4828–4837 [Google Scholar]
- WANG Ke, XU Mingliang, LI Yafei, et al. A robust learning model for deck motion prediction of aircraft carrier[J]. Acta Automatica Sinica, 2021, 48(1): 1–9 (in Chinese) [Google Scholar]
- SCHULZ E, SPEEKENBRINK M, KRAUSE A. A tutorial on Gaussian process regression: modelling, exploring, and exploiting functions[J]. Journal of Mathematical Psychology, 2018, 85: 1–16 [Article] [CrossRef] [Google Scholar]
- WILSON A, ADAMS R. Gaussian process kernels for pattern discovery and extrapolation[C]//Proceedings of the 30th International Conference on Machine Learning, PMLR, 2013: 1067–1075 [Google Scholar]
- YANG Yidong, YU Junya. Shipboard aircraft landing guidance and control[M]. Beijing: Defense Industry Press, 2007 (in Chinese) [Google Scholar]
- HODGES L H, SCHON D A. An analysis of teminal flight path control in carrier landing[R]. AD606040, 1970 [Google Scholar]
All Figures
|
图1 NKN结构图 |
| In the text | |
|
图2 甲板沉浮运动预测对比图 |
| In the text | |
|
图3 甲板沉浮运动预测误差绝对值 |
| In the text | |
|
图4 甲板沉浮运动预测误差平方值 |
| In the text | |
|
图5 甲板沉浮运动预测均方误差和均方根误差 |
| In the text | |
|
图6 甲板沉浮运动预测局部放大图 |
| In the text | |
|
图7 甲板俯仰运动预测对比图 |
| In the text | |
|
图8 甲板俯仰运动预测误差绝对值 |
| In the text | |
|
图9 甲板俯仰运动预测误差平方值 |
| In the text | |
|
图10 甲板俯仰运动预测均方误差和均方根误差 |
| In the text | |
|
图11 甲板沉浮运动预测(5 s)对比图 |
| In the text | |
|
图12 甲板沉浮运动预测(5 s)误差绝对值 |
| In the text | |
|
图13 甲板沉浮运动预测对比图 |
| In the text | |
|
图14 甲板沉浮运动预测误差绝对值 |
| In the text | |
|
图15 甲板沉浮运动预测误差平方值 |
| In the text | |
|
图16 甲板沉浮运动预测均方误差和均方根误差 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.