| Issue |
JNWPU
Volume 43, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 269 - 277 | |
| DOI | https://doi.org/10.1051/jnwpu/20254320269 | |
| Published online | 04 June 2025 | |
A response prediction method based on direct transfer function
基于直接传递函数的响应预测方法
1
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
Scientific Research Management Department, Chinese Flight Test Establishment, Xi'an 710089, China
Received:
11
April
2024
The elastic vibration of a wing significantly affects the transfer alignment accuracy of an inertial guidance system. Therefore, the accurate prediction of the elastic vibration response that obtains critical positions on an aircraft is one of necessary prerequisites for implementing transfer alignment. To meet this requirement, a response prediction method based on the direct transfer function is proposed, using the direct transfer relationship between multiple structural vibration responses. The method does not rely on a dynamic model but directly predicts the response at the target position with the surrounding structural response, thus being implementable. Firstly, the ideal samples of a whole aircraft's vibration responses under various excitations are calculated and obtained. Then, a virtual distributional sensor network is established, and the proposed response prediction method is used to virtually predict and reconstruct the acceleration response at the specified position under various operating conditions. Finally, the response prediction method is validated with the standard aircraft response dataset and the large passenger aircraft trial flight dataset. The experimental results show that the predicted responses and the actual measurements agree very well, further validating the feasibility of the proposed response prediction method.
摘要
机翼的弹性振动会严重影响惯导系统的传递对准精度, 因此精确预计获取机体关键位置的弹性振动响应是实施传递对准的必要前提之一。针对这一需求, 利用结构多点振动响应之间的直接传递关系, 提出了一种基于直接传递函数的响应预测方法。该方法无需依托动力学模型, 用结构周围响应直接预测目标位置响应, 具有很好的可实施性。计算获得了其在多种激励下的全机振动响应理想样本; 设定了一个虚拟的分布式传感器网络, 利用提出的响应预测方法对指定位置的加速度响应进行了多种工况下的虚拟预测重构; 使用标准飞机响应数据集和大型客机试飞数据集验证了所提方法的准确性。实验表明, 响应预测结果与实测结果之间保持了良好的一致性, 进一步验证了所提出的响应预测方法的可行性。
Key words: response prediction / direct transfer function / aircraft / distributional sensor
关键字 : 振动响应预测 / 直接传递函数 / 航空工程 / 分布式传感器
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
惯性导航网络(inertial navigation network)是一项综合了力学、数学、光学、机电、计算机和控制等多个学科的先进技术，是现代科学技术的重要成果[1]。它不依赖于任何外部信息，完全依靠自身能力，在各种天气条件下都能够连续地进行三维定位和定向，具有自主性和隐蔽性，因此在飞机、导弹等重要载体上是不可或缺的核心导航设备。惯性导航系统的核心组件包括陀螺仪和加速度计，前者用于测量载体的角运动信息，后者用于测量载体的线运动信息[2–3]。
在飞行中，飞机面临着各种环境变化，例如舵面偏转、突发风暴或紊流、飞机机动、燃料消耗等。这些环境的变化会导致机体处于未知的振动环境中，从而对惯性导航网络的测量精度产生负面影响，并给惯性导航系统的传递对准和在线标定带来困难[4–6]。对于弹性飞机而言，主惯导数据的高精度无法真实反映机翼处的具体姿态，而机翼处的子惯导由于弹性变形的原因，也无法准确描述局部姿态。因此，需要利用传递对准技术对子惯导进行信息校准，将飞机上精确的主惯导系统作为信息源，对待对准的子惯导系统进行数据标定[7]。机载惯导系统的传递对准精度受到多种因素的影响，主要包括杆臂效应、挠曲变形、时间延迟等[8–9]。这些因素的存在严重影响了传递对准的精度，从而直接影响了飞行员对飞行姿态的判断。若无法获得实时准确的姿态信息，将会影响飞行任务的顺利完成。
因此，获得飞机关键位置的弹性振动响应是实施传递对准技术的必要前提之一。目前对于未知载荷下的响应预测方法，目前通常采用以下2种处理方式[10]。第一种是基于频响函数的方法[11–13]，该方法以载荷识别为基础，先通过已知点的响应进行载荷识别，之后利用辨识出来的载荷数据结合频响函数计算未知测点的振动响应。北京交通大学的胡伟钢等[14]研究了一种基于振动模态参与因子的时域识别方法，运用有限元模型进行模态分析，利用优化测点组的模态应变矩阵来估计结构振动模态参与因子，利用模态叠加原理得到结构整体的应变响应。Kammer等[15]采用最小二乘法在时域里构造了响应传递矩阵，之后结合测量点的响应来重构未测位置的振动响应；随后Zhan等[16–17]又在未知不相关多源负载情况下，利用传递函数和进行负载识别和响应预测。然而，上述方法在未知激励的条件下难以精确预测飞机的弹性响应。第二种是基于机器学习的响应预测方法[18–19]，该方法将已知点响应作为输入，未知点响应作为输出，利用大量的试验数据，直接构造输入和输出的线性网络传递关系，该方法主要有回归方法、支持向量机方法、神经网络方法等[20]。Mao等[21]研究了基于多输入多输出支持向量机的载荷识别方法。在响应预测领域，张宜群[22]采用SVM方法对做某船舶振动响应进行预测。翟东武等[23]用神经网络进行结构响应和控制信号的时滞补偿，通过基于多层前馈网络的预测控制算法对多层结构进行振动响应控制。然而，机器学习方法是一种依赖于先验数据的处理方法，难以应对数据集不完备的情况。因此，寻找一种既不依赖于载荷，又能够利用飞机上各个响应之间相关性或传递特性进行振动响应预测的技术，对于传递对准方法的发展具有重要的实际意义。
为此，本文提出了一种基于直接传递函数的响应预测方法。该方法利用弹性结构多点振动响应与振动响应之间的直接传递关系，根据分布式传感器数据对指定位置的振动响应进行预测。这一方法不仅可以为后续惯性导航系统的传递对准技术提供可参考数据，还为分布式机载惯导系统的传递对准提供了一种新的补偿方案。
1 基于直接传递函数的响应预测方法原理
现假设存在一个n自由度的线性时不变系统, 其所受载荷向量(频域内)为F ={F1(ω), F2(ω), …, Fn(ω)}T, 在每个自由度上产生的实际工作响应(operational response)为Xop={X1op(ω), X2op(ω), …, Xnop(ω)}T。则根据结构动力学基本原理, 载荷向量与实际工作响应向量之间应该满足如下关系
式中：H表示n自由度系统的频响函数矩阵; Z表示n自由度系统的阻抗矩阵, Z-1=H; F表示n自由度系统上施加的载荷向量; Xop表示n自由度系统的实际工作响应向量。
对于n自由度系统中任意2个自由度i, j, 它们之间的频响函数可以表示为
式中：Hij表示第j个自由度到第i个自由度的频响函数; XijG表示只在第j个自由度施加激励时, 第i个自由度的响应; Fj表示第j个自由度上所施加的载荷。
(1) 式可视为振动响应的一种解析方法。该方程表明, 在已知载荷数据的情况下, 任何自由度上的响应都可以表示为各自受到载荷影响的线性组合, 其组合系数即为系统的频响函数。基于已知载荷数据, 可以使用频响函数矩阵计算任何自由度的响应数据, 这也是结构动力学领域中最基本的响应计算问题之一。然而, 在未知载荷的情况下, (1)式无法进行响应计算。因此, 在未知载荷的情况下, 本文试图解决的核心问题是基于每个自由度的响应与响应之间的传递关系, 直接利用已知点响应数据进行目标点响应的预测。
对于n自由度系统中任意2个自由度i, j, 两者之间响应的传递函数可以表示为
式中：XijG表示F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第i个自由度的响应; Xjext表示F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第j个自由度的响应, 即载荷分量Fj单独作用于系统时j点的原点响应。
将(3)式命名为全局传递函数(global transfer function, GTF), 这个传递函数是可测的, 并且在测试时整个全局系统都处于振动状态, 因此在传递过程中需要考虑所有的传递路径。
利用全局传递函数矩阵, n自由度线性时不变系统的实际工作响应信号Xop可以分解成如下形式
式中：Xop表示n自由度系统的实际响应向量; TG表示n自由度系统的全局传递函数矩阵; Xext表示每个载荷分量单独作用于系统时原点响应所构成的向量。(4)式可以认为是振动响应的另一种分解方式。该式表明, 任意一个自由度上的工作响应, 都可以表示成每个自由度上载荷分量单独作用时原点响应的线性组合, 组合系数就是系统的全局传递函数。
自由度i上的实际工作响应可以表示为该点上载荷分量单独作用时原点响应和剩余自由度实际工作响应的线性组合。因此, 问题的关键在于是否存在一种能够准确描述上述响应传递关系的函数。
现假设存在一种传递函数矩阵TD, n自由度系统中任意一自由度i的实际工作响应Xiop可以进行如下分解: 一部分是作用于该自由度自身的外部激励Fi所引起的原点响应; 另一部分则是由除i点外, 剩余与i直接关联自由度的实际工作响应直接传递到该点的响应所引起。其中的组合系数就是所假设矩阵TD中的元素。这种假设的响应分解方式可以用(5)式来表示。
联立(4)式和(5)式, 可以得到全局传递函数矩阵TG和假设的传递函数矩阵TD之间的关系为
式中，diag(·)表示只保留矩阵的非对角元素。
通过(6)式可以得到全局传递函数矩阵TG和传递函数矩阵TD中各个元素之间的对应关系为
通过(7)式, 可以发现矩阵TD中的元素和全局传递函数矩阵TG中的元素是一一对应的, 这也说明了传递函数矩阵TD的唯一存在性, 并且可以利用全局传递函数矩阵来计算获得。将传递函数矩阵TD命名为直接传递函数矩阵(direct transfer function)。因为其中的元素TijD代表了2个自由度实际响应之间的直接传递关系, 与其余的自由度无关, 在响应传递过程中, 只考虑2个自由度之间的直接传递路径。
根据(7)式中直接传递函数矩阵和全局传递函数矩阵元素之间的关系, 可以得到直接传递函数矩阵中的对角元素为
非对角元素为
对(8)式的分子和分母同时乘以Fi可得
式中，Xiext=HiiFi, 其物理含义较为容易理解, 即当系统仅在第i自由度作用载荷Fi时, 第i点的响应。
根据(7)式可得
通过将原n自由度系统除i, j以外自由度加以约束, 并在j自由度施加激励, 引入方程
式中, XijD和XjjD的物理含义为系统仅第i和第j个自由度无约束而其他自由度均被约束时, 在第j个自由度作用Fj时，分别在第i和第j个自由度所激起的响应。
所以
通过(10)式和(13)式, 可以得到直接传递函数的定义，如(14)式所示。
式中, XijD表示除i, j外, 其余自由度全部约束之后, F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第i个自由度的响应。XjjD表示除i, j外, 其余自由度全部约束之后, F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第j个自由度的响应。
直接传递函数矩阵中的非对角元素TijD, 就是在Xm=0(m≠i, j)的前提下, 在第j个自由度加激励, 第i个自由度响应与第j个自由度响应之比。
i到i的原点直接传递函数表达式为
式中, X′i表示除i点外, 其余自由度全部约束之后, F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第i个自由度的响应。Xiext表示无约束条件下, F={0, 0, …, Fj(ω), …, 0}T作用于系统时, 第i个自由度的响应。
(5) 式建立了一种基于直接传递函数的响应分解关系, 这种分解关系可以用于本文的响应预测。假设系统任意一自由度i处的响应Xiop未知, 若已知周围节点的工作响应及目标点自身激励引起的原点响应Xiext, 则由(5)式可以有
2 基于直接传递函数的响应预测方法实验验证
第1节详细介绍了基于直接传递函数的响应预测方法的基本原理。本节将以弹性飞机结构动力学标模和大型客机试飞数据集为研究对象, 设计虚拟的响应预测试验, 以验证提出的基于全局直接传递函数的响应预测方法的可行性。
首先, 使用ABAQUS有限元分析软件建立了一个大展弦比长直机翼的飞机标准模型, 并进行了频率分析步骤仿真计算, 以获得有限元模型的固有频率和振型。随后, 利用模态稳态动力学分析步骤进行频响分析, 得到有限元模型的频响函数矩阵。接着, 利用(14)式计算直接传递函数, 获得飞机有限元模型的直接传递函数矩阵。
传感器的安装位置分别位于左翼尖、右翼尖、重心、机头和尾翼。激励方式为冲击激励、冲击激励、方波激励以及随机激励。每种激励加载方式包括重心加载、左翼尖非对称加载以及左右翼尖对称加载。使用其中4个点的仿真响应数据, 利用直接传递函数对左翼尖部位的振动响应数据进行预测, 然后与左翼尖的响应仿真数据进行对比。最后, 计算每种加载形式和加载位置的预测结果的均方根误差和吻合度, 并利用这些指标对仿真预测结果进行评估。图 1给出了本节的研究流程。
 |
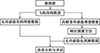图1 响应预测流程 |
2.1 有限元模型的建立与仿真计算结果
2.1.1 有限元模型介绍
有限元建模过程中机翼和尾翼均采用壳单元进行模拟, 机身采用等截面矩形梁单元进行模拟, 图 2给出了所建立的标准飞机仿真模型。
 |
图2 标准飞机仿真模型 |
全机结构动力学有限元模型中，材料选用铝材, 弹性模量取71 GPa, 密度取2 700 kg/m3, 泊松比取0.3。整个有限元模型包括38个节点, 162个单元, 其中132个壳单元, 30个梁单元。模型翼展长2.04 m, 机身长1.5 m, 总质量为27 kg。阻尼施加采用模态阻尼输入方式, 设计各阶模态阻尼比为0.01。
设定1组虚拟的分布式传感器网络, 选择5个位置作为传感器安装位置, 分别是重心、右翼尖、左翼尖、机头和尾翼, 图 3给出了传感器布置图。
 |
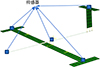图3 虚拟传感器分布位置图 |
2.1.2 弹性飞机模型的固有特性计算结果
首先利用频率分析步计算飞机模型自由状态下的固有频率。在得到全机模型的固有特性后, 依次对安装传感器的5个位置施加单位力, 利用模态稳态动力学分析步对弹性飞机有限元模型进行稳态分析, 仿真获得了传感器安装位置之间的频响函数, 根据仿真得到的频响函数数据, 利用(3)式可以计算飞机有限元模型的全局传递函数矩阵, 之后利用全局传递函数和直接传递函数之间的关系式计算安装传感器5个位置之间的直接传递函数矩阵。响应预测过程中由于只考虑了竖直方向平动自由度, 因此最终得到的直接传递函数矩阵是一个5×5的复数方阵, 里面包含了幅值和相位信息。在实际工程运用中, 应根据所研究的目标结构复杂程度适当地增加自由度, 比如x方向、y方向平动或者旋转自由度, 相应的矩阵阶数也会随之增加。
2.2 不同形式激励下的响应预测
利用模态动力学分析步, 对模型施加冲击激励、冲击激励、方波激励以及随机激励等多种载荷激励, 仿真计算获得了安装传感器位置的弹性振动响应理想样本。每种激励方式都设置了不同的加载位置, 包括重心加载、左翼尖非对称加载以及左右翼尖对称加载3种方式。之后将其中4个点的仿真响应数据作为高精度传感器的无误差测试数据, 利用直接传递函数对左翼尖部位的振动响应数据进行预测重构, 并与左翼尖的响应仿真数据进行对比。给出了仿真计算响应和预测响应时频域对比图。计算了每种加载形式和加载位置下预测结果的均方根误差和样本吻合度。利用均方根误差、样本吻合度以及相关系数对仿真预测结果进行评估。
2.2.1 预测结果有效性评估方法
均方根误差计算方法如(17)式所示。
式中：ERMS表示仿真数据与预测数据之间的均方根误差; X(i)表示仿真计算得到的响应数据;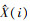 
表示预测重构得到的响应数据; N表示时域点个数。
仿真结果与预测结果之间的样本吻合度计算公式如(18)式所示。
式中, X表示X的平均值。
仿真结果与预测结果之间的相关系数计算公式如(19)式所示。
式中：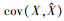
表示仿真数据与预测数据之间的协方差; var(X)表示仿真数据的方差; 
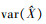表示预测数据的方差。
2.2.2 不同激励作用下的响应预测结果
本节讨论了本文方法在不同工况下的响应预测结果，包括冲击激励、冲击激励、方波激励和随机激励。激励施加情况如表 1所示。
以冲击激励为例，针对重心加载、左翼尖非对称加载和左右翼尖对称加载3种工况，最终得到的响应预测结果如下。
从图 4a)可以看出，当冲击激励施加于重心处时，左翼尖处的加速度时域响应的预测曲线和仿真曲线基本上完全重合。从幅频曲线对比图 4b)中可以看出，仿真数据和预测响应的幅频曲线重合度很好。说明当在重心处施加冲击激励时，直接传递函数法对于强迫振动响应具有很高的预测精度。从图 4c)~4d)可以看出，当冲击激励施加于左翼尖处时，对原点激励加以考虑后，激振频率点处对应的幅值预测结果非常好。振动响应的预测结果重合度高。从图 4e)~4f)可以看出，在左右翼尖处施加对称冲击激励时，其预测结果和非对称激励作用下基本一致，对原点激励贡献加以考虑后，预测精度高。总体来说，对称加载的响应预测结果优于非对称加载的响应预测结果。
 |
图4 施加冲击激励时的响应预测结果 |
表 2~4给出了不同激励形式和不同加载方式下响应预测结果的均方根误差和吻合度。
从表 2~4可以看出，当载荷施加于重心位置时，左翼尖的预测精度很高，4种激励形式下吻合度均能达到90%以上，相关系数均在0.99以上，说明当目标点没有载荷作用时，预测结果与仿真结果有很高的一致性，基于直接传递函数的响应预测方法具有很高的预测精度。当载荷施加于左翼尖位置时，当考虑原点载荷的贡献时，预测精度能够得到显著提高，吻合度能达到80%左右，相关系数也有很大改善。当载荷对称施加于左右翼尖位置时，当考虑原点载荷的贡献时，预测结果的吻合度甚至能达到90%以上，相关系数也基本能达到0.99。说明当待预测位置存在载荷时，需要对载荷贡献进行补偿和修正，才能保持良好的预测精度。总体来说，各种形式激励下，对称加载时的预测效果明显优于非对称加载。
在本次虚拟验证试验中，每个位置的振动响应均是没有被误差污染的，所以这一部分误差主要是结构离散化带来的，因此，为了更好地控制误差，需要根据结构，选择更合适的传感器网络。
激励施加情况
重心处加载的响应预测误差
左翼尖非对称加载的响应预测误差
左右翼尖对称加载的响应预测误差
2.3 大型客机试飞数据集验证
为了进一步评估所提模型在真实工程环境下的验证能力，使用了大型客机在紊流激励下的振动响应试飞数据集，飞行高度4 572 m, 速度426 km/h。紊流激励主要是利用飞机稳定平飞时受到外界气动力来对飞机产生自然的激励作用。在飞机左右机翼翼尖前缘和后缘、左右机翼翼中前缘和后缘、垂尾翼尖前缘和后缘、垂尾中部前缘和后缘、左右平尾翼尖前缘和后缘、左右平尾中部前缘和后缘、机身头部、中部和后部、各活动舵面、发动机、小翼等部位共安装59个振动加速度传感器及其配套的信号调节设备和记录设备，按照顺序分别编为1~59号，如图 5所示。
 |
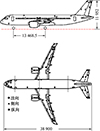图5 大型客机传感器安装位置 |
分析的时间跨度为62.463 0 s，时间步长为0.002 s(共31 232个采样点，记为n=31 232)。将所有加载条件下采集的振动响应数据作为样本处理。选择机翼处的加速度作为目标响应，为左机翼前缘尖Z向振动加速度ANW1，它的编号为1号。使用剩余58个响应数据作为已知响应数据。
使用上述目标响应数据和已知响应数据训练模型并计算，将预测响应与实际响应进行了比较。目标点的响应预测结果如图 6所示。观察图 6中的结果，可以看到预测结果和实际测试结果吻合较好，说明本文方法在真实的工程环境中同样适用。
 |
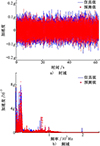图6 试验响应与预测响应对比 |
3 结论
为了获得飞机关键位置的弹性振动响应，提出了一种基于直接传递函数的响应预测方法。该方法首先利用频率分析得到固有频率，之后进行频响分析获得模型的频响函数矩阵，最后建立了一种基于直接传递函数的响应分解关系，用于响应预测。本文以一个弹性飞机结构动力学标模和大型客机为研究对象，对基于全局直接传递函数的响应预测方法进行了验证。检验了模型在不同加载位置和不同载荷形式下的响应预测能力。验证结果表明，当在重心处加载时，对于不同类型激励下的飞机振动响应预测结果精度都很高。所以，本文方法在知道原点载荷数据的前提下可以很好地预测未知点的响应。在大型客机试飞数据集上的验证也证明了本文方法的有效性。总的来说，本文方法可以很好地预测目标点的响应。
References
- KELLEY R T, CARLSON N A, BERNING S. Integrated inertial network[C]//Position Location and Navigation Symposium, 1994: 439-446 [Google Scholar]
- LYU Zhigang, WU Shuang, BAI Long. Development status and key technology analysis of fiber optic inertial navigation at home and abroad[J]. Digital Ocean and Underwater Offense and Defense, 2020, 3(5): 420–424 (in Chinese) [Google Scholar]
- XIA Gang. Research progress and development trend of inertial navigation platform system[J]. Navigation and Control, 2020, 19(4/5): 126–134 (in Chinese) [Google Scholar]
- BI Kai. Research on online calibration and compensation technology of MEMS inertial navigation system[D]. Xi'an: Xi'an University of Architecture and Technology, 2020 (in Chinese) [Google Scholar]
- WANG Jie. Research on online calibration, compensation, and dynamic accuracy evaluation technology of high-precision inertial navigation system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 (in Chinese) [Google Scholar]
- WANG Hailiang, SHI Zhiyong, LI Guozhang, et al. Research on a simple online calibration scheme for strapdown inertial navigation in projectiles[J]. Journal of Gun Launch and Control, 2018, 39(4): 6–10 (in Chinese) [Google Scholar]
- CHEN Weina, YANG Zhong, GU Shanshan, et al. The transfer alignment method based on the inertial network[J]. Optik, 2020, 217: 164912 [Article] [Google Scholar]
- WANG Si. Research on rapid transfer alignment of strapdown inertial navigation system for tactical guided weapons[J]. Harbin: Harbin Institute of Technology, 2008 (in Chinese) [Google Scholar]
- FANG Qun, DING Yingying, YUAN Jianping. Research on rapid transfer alignment method for airborne missile strapdown inertial navigation system[J]. Flight Mechanics, 2001(4): 49–53 (in Chinese) [Google Scholar]
- ZHOU Dawang, ZHAO Guorong, XU Shenghong, et al. Comprehensive compensation method for flexural deformation errors in master/slave inertial navigation calibration[J]. Control and Decision, 2016, 31(4): 709–716 (in Chinese) [Google Scholar]
- NISHIMOTO H, AKAGI M, KITAMURA T, et al. Estimation of transfer function of vocal tract extracted from MRI data by FEM[J]. IEICE Technical Report Speech, 2004, 10(3): 31–36 [Google Scholar]
- PAIK I, ROESSET J M. Use of quadratic transfer functions to predict response of tension leg platforms[J]. Journal of Engineering Mechanics, 2016, 122(9): 882–889 [Google Scholar]
- ALBERT C G, VERONESI G, NIJMAN E, et al. Prediction of the vibro-acoustic response of a structure-liner-fluid system based on a patch transfer function approach and direct experimental subsystem characterization[J]. Applied Acoustics, 2017, 11(2): 14–24 [Google Scholar]
- HU Weigang, LIU Zhiming, WANG Xiet al.. Research on identification of time-domain modal participation factors based on measured strain[J]. Journal of the Railway Society, 2018, 40(2): 45–51 (in Chinese) [Google Scholar]
- KAMMER D C. Estimation of structural response using remote sensor locations[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(3): 501–508 [Google Scholar]
- ZHAN Wei, WANG Cheng. Transfer functions and loads identification based response prediction in situation of unknown uncorrelated multi-source loads[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 59(3): 1029–1039 [Google Scholar]
- ZHAN Wei, WANG Cheng. Multivariant linear regression model based response prediction in situation of unknown uncorrelated multiple sources load[C]//28th International Conference on Vibroengineering, 2017: 271-277 [Google Scholar]
- CUI Zhenkai, WANG Cheng, HE Ting, et al. Multi-point frequency domain vibration response prediction based on deep transfer learning[J]. Computer Integrated Manufacturing Systems, 2023, 29(8): 2524–2536 (in Chinese) [Google Scholar]
- WANG Cheng, ZHAN Wei, LI Haibo, et al. Multi-point vibration response prediction based on principal component regression under multiple unknown loads[J]. Computer Integrated Manufacturing Systems, 2019, 25(3): 576–585 (in Chinese) [Google Scholar]
- MARQUET T, OSWALD E. A comparison of multi-task learning and single-task learning approaches[C]//International Conference on Applied Cryptography and Network Security, Cham, 2023: 121-138 [Google Scholar]
- MAO W, TIAN M, YAN G. Research of load identification based on multiple-input multiple-output SVM model selection[J]. Journal of Mechanical Engineering Science, 2012, 226(5): 1395–1409 [Google Scholar]
- ZHANG Yiqun. Prediction of the vibration of ship's supertructure cabin based on SVM method[D]. Harbin: Harbin Engineering University, 2008 (in Chinese) [Google Scholar]
- ZHAI Dongwu, ZHU Xi. Prediction control of structuralvibration response basedon neural network[J]. Journal of Tsinghua University, 2002, 40(suppl. 1): 61–65 (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 响应预测流程 |
| In the text | |
|
图2 标准飞机仿真模型 |
| In the text | |
|
图3 虚拟传感器分布位置图 |
| In the text | |
|
图4 施加冲击激励时的响应预测结果 |
| In the text | |
|
图5 大型客机传感器安装位置 |
| In the text | |
|
图6 试验响应与预测响应对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.