| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 11 - 17 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210011 | |
| Published online | 29 March 2024 | |
Study of GSO-GL based secondary source configuration optimization method for broadband sound field reproduction
宽带声场再现中基于GSO-GL的次级声源布局优化方法研究
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
2
Zhijiang Lab, Hangzhou 311121, China
Received:
16
March
2023
Sound field reproduction is a method that uses multiple secondary sound sources to reproduce a predefined desired sound field in a listening area. The configuration of the secondary sound sources is a key factor affecting the reproduction performances. To optimize the secondary source configuration, this study proposes a new method that combines the Gram-Schmidt orthogonalization method with the group Lasso method, which is called GSO-GL method. Firstly, it selects a certain number of the secondary sources from all the alternative secondary sources using the Gram-Schmidt orthogonalization method. The excitation sources are then further selected from the secondary sources selected in the previous step using the group Lasso method. The sound field simulation from the 2D room model show that the GSO-GL method outperforms the Gram-Schmidt orthogonalization method or the group Lasso method alone, combining the high system stability of the Gram-Schmidt orthogonalization method with the high reproduction accuracy of the group Lasso method.
摘要
声场再现是一种利用多个次级声源在听音区域内再现预定义期望声场的方法, 其中次级声源布局是影响再现性能的关键因素。为解决次级声源布局优化问题, 提出一种将Gram-Schmidt正交化方法与组Lasso方法相结合的方法(称为GSO-GL方法), 即先使用Gram-Schmidt正交化方法从所有备选次级声源中选出一定数量的次级声源, 再利用组Lasso方法从前一步所选的次级声源中进一步选择出激励声源。二维房间模型仿真结果表明, GSO-GL方法的性能优于单独使用Gram-Schmidt正交化方法或组Lasso方法, 综合了Gram-Schmidt正交化方法的高系统稳定性和组Lasso方法的高再现准确度。
Key words: sound field reproduction / secondary source configuration optimization / group Lasso / Gram-Schmidt orthogonalization
关键字 : 声场再现 / 次级声源布局优化 / 组Lasso / Gram-Schmidt正交化
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
声场再现(sound field reproduction, SFR)又称为声场重放或声场重现,是利用1组次级声源再现预定义期望声场的方法[1],广泛应用于空间听觉、个人音频和噪声控制等领域。例如在噪声控制中,利用该技术可再现飞机舱室内部噪声场,以评估有源噪声控制系统的性能。期望声场可由传声器阵列测量得到,也可使用多个虚拟声源进行数学建模得到[1]。目前主流的SFR方法有2类:一类是解析法,其核心为由Helmholtz方程解析推导得出边界积分方程,如波场合成[2]、高阶Ambisonics[3];另一类是匹配法,它基于控制期望声场中离散点处的声学参量从而得到次级声源强度,如声压匹配法(pressure matching, PM)[4]。由于PM通过构造线性回归问题求解次级声源的驱动信号,对传声器(控制点)和次级声源的布局约束较小,故在诸如舱室SFR等实际应用中,许多学者采用该方法[5-6]。
影响SFR系统再现性能的因素有很多,其中次级声源的布局(个数和位置)尤为重要。在实际工程应用中,由于设备体积和成本等因素的限制,往往需要限制次级声源的个数,因此需要优化布局以便在次级声源个数较少时也能获得良好的SFR性能。布局优化一般视为组合优化问题,即从大量备选位置中选取一定数量的位置来布放次级声源使得再现性能尽可能好。通常,人们使用遗传算法、模拟退火(simulated annealing, SA)等自然算法进行求解[6-7],但这些算法的性能易受所选参数影响,且所得解随机性较大。Asano等[8]采用Gram-Schmidt正交化(Gram-Schmidt orthogonalization, GSO)解决该优化问题,但在备选次级声源位置较多时,会由于矩阵构造困难导致算法性能下降。Lilis等[9]提出将最小绝对收缩和选择算子(least-absolute shrinkage and selection operator, Lasso)用于布局优化中,它利用期望声场的某些稀疏性先验信息,在欠采样情况下具有比最小二乘(least squares, LS)方法更好地再现准确度及稳定性。
实际中的声场多为宽带声场,因此上述方法需要扩展到能同时考虑多频点的形式。SA等自然算法可以结合各频点下的代价函数构造新的多频点代价函数[10]。GSO方法也类似地构造了新的代价函数[8]。Radmanesh等[11]针对Lasso提出了联合Lasso-LS两步算法,先在各频点下使用Lasso选取次级声源,再做并集得到多频点的次级声源布局,但该方法难以分配各频点下的次级声源激励个数,特别是当所要求的次级声源激励个数较少时,有碍实际工程应用。
Yuan等[12]提出的组Lasso模型是一种具有组稀疏性的模型。Gauthier等[13]将组Lasso应用于考虑单个频点的SFR,其将多个次级声源作为1组以优化次级声源布局。进一步地,Lilis等[9]提及利用组Lasso处理宽带多频点问题的思路,但并未展开深入研究。
本文基于上述研究进展,提出将组Lasso应用于宽带SFR中,并在考虑到组Lasso方法和GSO方法各自具有的SFR特性后,将组Lasso方法与GSO方法联合,即成为联合GSO和组Lasso的两步GSO-GL方法。本文首先对次级声源布局优化问题进行阐述,介绍了GSO方法,提出应用于宽带SFR的组Lasso方法,将上述2种方法联合成为GSO-GL方法。将GSO-GL方法与SA方法、GSO方法及组Lasso方法进行比较,并研究了混响与GSO-GL方法中使用GSO所选次级声源个数对再现性能的影响。仿真结果表明,GSO-GL方法结合了GSO方法的高系统稳定性和组Lasso方法的高再现准确度,在次级声源个数较少时依然能实现较好的SFR性能。
1 次级声源布局优化问题
SFR旨在使用1组次级声源再现目标区域Ω内的期望声场,即最小化以下目标函数
式中,f为频率(以下为描述简洁将其省略)。p(x)为目标区域内x点处的期望声压,prep(x)为目标区域内x点处的再现声压。当系统中有L个次级声源时, 该再现声场表示为
式中:ql为第l个次级声源的源强;zl(x)为第l个次级声源到x点处的声传递阻抗, 在自由场中
式中:i为虚数单位;ρ0为介质密度;c0为声速, k为波数;xl为第l个次级声源的位置。
当次级声源布局确定时, 最小化目标函数(1)式即可确定次级声源源强, 故如何对次级声源进行布局便成为影响SFR性能的关键因素。次级声源布局优化问题即从预先确定的众多备选次级声源位置中选择再现性能最优的布局, 该布局中所选位置处布放的次级声源即为激励声源, 用于再现声场。激励声源需要使Ω内的再现声场尽可能地接近期望声场, 同时激励声源的源强需要受到约束以保证SFR的稳定性。若存在L个备选次级声源, 其位置的集合可记为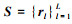 。从中选择L1个激励声源, 则可能的组合个数为CLL1, 激励声源布局S1⊂S。假设SFR评价指标为F(S1), 其值越大表示该布局再现性能越优, 那么次级声源布局优化问题可由(4)式表示
。从中选择L1个激励声源, 则可能的组合个数为CLL1, 激励声源布局S1⊂S。假设SFR评价指标为F(S1), 其值越大表示该布局再现性能越优, 那么次级声源布局优化问题可由(4)式表示
需要注意的是, (4)式仅为次级声源布局优化问题的定性表示, 即希望再现性能指标尽可能优秀, 而非布局优化方法的具体优化准则, 因为诸如GSO方法并非直接以SFR性能指标作为目标函数。
布局优化包括个数优化和位置优化, 但由于实际工程中设备信号通道数有限, 激励声源个数可以给定, 因此本文的布局优化主要针对给定激励个数时激励声源的位置选择。
2 联合Gram-Schmidt正交化和组Lasso两步方法
本文提出适用于宽带SFR的组Lasso方法, 并将GSO方法与之联合成为一种新的两步方法, 称为GSO-GL方法, 旨在兼顾GSO方法的高系统稳定性与组Lasso方法的高再现准确度。GSO-GL方法先利用GSO方法从所有备选次级声源中选出部分次级声源, 再利用组Lasso方法从前一步GSO方法所选的次级声源中进一步选择部分次级声源作为激励声源。
以下给出GSO方法及组Lasso方法的原理与步骤, 并研究其特性。
2.1 GSO方法
GSO方法的优化准则是使所选次级声源对应的声传递阻抗向量最大程度地线性无关。若激励声源构成的声传递阻抗矩阵Z∈CM×L, 其中M为控制点个数, L为激励声源个数, 则其每列zl对应第l个激励声源。声传递阻抗包含了次级声源到控制点之间的空间信息, 若Z中有与zl线性相关的列, 那么zl对应的激励声源作用可由其他激励声源替代, 因此该激励声源是可以剔除的。
GSO方法的选择过程为:首个激励声源的选择准则是该源对应的传递阻抗zl与期望声压p接近; 第l个传递阻抗向量zl投影至正交基uj(j∈{1, ⋯, k-1})张成的子空间上。第k步中选择的次级源lk需要使zl和其投影之间的残差el的二范数最大化
由此第k个正交基uk = el/‖el‖2。
对于宽带声场, 只需在计算所有频点的el后, 在整个频带内对el进行加权平均即可。在参考文献[8, 14]中具体描述了GSO方法。
2.2 适用于宽带SFR的频域组Lasso方法
组Lasso模型是一种具有预设组效应的稀疏模型, 能够根据实际问题预先设定分组, 并且分组情况完全由人为控制。在本问题中, 本文提出人为地将第l个次级声源的声传递特性设定为第l组, 组内元素为各频点上该次级声源到各控制点的声传递阻抗。组Lasso模型中同一个组中元素将同时被模型选中或移除, 即第l个次级声源的所有声传递阻抗将同时被优化问题考虑或排除, 这便实现了控制次级声源个数及次级声源布局优化的目的。
假设有M个控制点, L个次级声源, N个频点, 则组Lasso方法的宽带SFR表达式可写为
pnm为第n个控制点处在第m个频点上的复声压。
按照以下形式构造Z, 即将Z分为L组
znlm为第n个频点上, 第l个次级声源到第m个控制点的声传递阻抗。
并将q也分为L组
qnl为第l个次级声源在第n个频点上的声源强度。此外, 期望声场为d∈CNM×1, 且误差为e =d-Zq。
由此, 组Lasso的代价函数可以表示为
式中:  为再现误差二范数; ‖ql‖2为组二范数。
为再现误差二范数; ‖ql‖2为组二范数。 为组二范数的一范数, 组级别的一范数即在组间引入了稀疏性。
为组二范数的一范数, 组级别的一范数即在组间引入了稀疏性。
那么, 组Lasso的目标即为寻找一组qβ, 使Jβ最小
在参考文献[12]中给出了组Lasso的解法。
2.3 组Lasso方法中的参数调节
代价函数(12)式中的β为稀疏度调节参数, 在组Lasso中, 其作用是调节组间的稀疏度, 即改变激励声源的个数; 而不改变各组内的稀疏度, 即激励声源在宽带范围内的各频点都将被激励。β的调节方式一般有2种:一种是基于对控制点处再现声场的交叉验证, 另一种则是调节β使激励声源个数满足用户所需。在这2种方法中, 第一种方法虽然较复杂且对计算量有一定的要求, 但其比第二种方法更严谨[13]。然而第一种方法无法直接控制解的稀疏度, 即激励声源个数, 不符合本文的要求, 故本文使用第二种方法对β进行调节。
参数β可在(0, max(‖Z1Hp‖, ⋯, ‖Z LHp‖))该范围内选取, β值越大, 激励声源个数越少。将该选取范围以均匀或对数间隔方式取多个β值, 选择满足激励声源个数要求的最小β值为最终值。
2.4 GSO-GL方法
GSO方法具有较高的系统稳定性, 而组Lasso方法具有较高的再现准确度, 因此可以将GSO方法与组Lasso方法相结合, 以期望能综合上述2种方法各自的优势。GSO-GL方法先利用GSO方法从全部L1个备选次级声源中选出L2个次级声源, 若希望系统具有更好的系统稳定性指标, 则减小L2值, 而若希望系统具有更好的再现准确度指标, 则增加L2值; 再利用组Lasso从前一步GSO方法所选的L2个次级声源中进一步选择L3个次级声源作为激励声源, 组Lasso的β值由L3的大小确定, L3越小, 则β值越大。
图 1给出GSO-GL方法优化布局流程。
 |
图1 GSO-GL方法优化布局流程 |
3 仿真模型构建与SFR评价指标
3.1 模型构建
在SFR的算法研究与实际工程应用中, 为了降低系统复杂度, 一般将再现区域设置为人耳所处的二维平面内。因此, 不失一般性, 本文考虑二维空间SFR, 其模型如图 2所示, 该房间模型参考文献[14]的参数设置。本文使用有限元方法计算声传递阻抗。房间内部介质为空气, 其声速为343 m/s。房间的4个壁面吸声系数分别设置为0.1和0.5来模拟高混响和低混响环境。100个备选次级声源均匀分布于中心坐标为(2.5, 2), 长宽为3 m×2 m的矩形边界上, 并以“×”表示; 20个控制点均匀分布在圆心为(2.5, 2), 半径分别为0.5和0.25 m的圆上, 并以“·”表示。再现区域为圆心为(2.5, 2), 半径为0.5 m红色圆的内部区域, 期望声场为平面波, 其到达角度为10°~360°并以10°为间隔, 考察频点为100 Hz到400 Hz并以5 Hz为间隔。在具体工程问题中, 只需按照工程需求对本模型的形状、边界条件以及内部控制点和备选次级声源位置等参数进行设定, 即可使用本文提出的方法进行次级声源的布局优化。
 |
图2 二维SFR房间模型 |
3.2 评价指标
为量化不同次级声源布局优化方法的效果, 本文从再现准确度以及系统稳定性2个角度对评价次级声源布局优化方法性能的指标进行定义。
1) 再现准确度指标
控制点处归一化再现误差E
模态置信度准则MAC(modal assurance criterion, MAC)
MAC表示真实数值(期望声场)与估计数值(再现声场)的相似度, 其取值范围通常为0(无相似性)到1(完全相似)之间。使用中心为(2.5, 2), 间距为0.05 m的均匀分布格点对再现区域进行监测, 其中dmon为监测点处期望声压向量,pmon为监测点处再现声压向量。
2) 系统稳定性指标
声传递阻抗构造矩阵Z的条件数κ
使用条件数κ表征Z是否为良态。若κ很大, 那么Z将成为病态矩阵, 其对外界摄动会比较敏感。
激励声源控制功率P
其为激励声源输出功率的量度, 在实际应用中需要对其进行限制。当P过大时, 会引起激励声源(扬声器)的非线性响应, 影响系统稳定性。
在后续仿真中,以上指标均为各平面波入射角度下指标的均值。
4 SFR仿真结果与分析
4.1 低混响条件下4种方法的SFR结果
图 3给出了在壁面吸声系数为0.5的低混响环境中,从100个备选次级声源中选择6个激励声源进行SFR时,4种方法的评价指标,其中组Lasso方法用GLasso表示,GSO-GL方法用GSOGL表示。SA算法初始温度为1 000℃,终止温度为10-3℃,链长为200,降温速率为0.9;由于SA算法具有随机性,以下结果为运行5次得到的平均结果。在利用以上方法选中次级声源后,使用LS方法得到激励声源强度,未使用正则化求解的目的是避免正则化参数的确定问题,同时凸显方程解对扰动的敏感性[10]。可以看出,由于SA算法直接以E作为代价函数,所以该指标领先GSO和组Lasso方法;但其MAC指标并未展现出明显优势,且系统稳定性指标较差;此外,SA方法具有较高的随机性,需要比较多次运行结果才能选择出较优的次级声源布局,这增加了优化运算时间和布局选择难度。GSO方法具有明显的系统稳定性优势,但其再现准确度指标相较SA和组Lasso方法表现不佳,特别是当频率较高时再现准确度有明显下降。本文提出的组Lasso方法在整个考察频带内均具有较好的再现准确度,特别是当频率较高时MAC依然能保持在0.8以上,但其系统稳定性指标最差。
GSO-GL方法先使用GSO方法选择19个次级声源,再利用组Lasso方法从19个次级声源中选出6个激励声源。由图 3可看出GSO-GL方法兼具组Lasso方法的高再现准确度和GSO方法的高系统稳定性,其中MAC指标在整个考察频带上均能高于0.8,且系统稳定性指标相较SA算法也具有明显优势。
 |
图3 低混响条件下不同布局方法的评价指标 |
4.2 高混响条件对SFR结果的影响
为研究GSO-GL方法的抗混响能力,图 4给出了在壁面吸声系数为0.1的高混响环境中,从100个备选次级声源中选择6个激励声源进行SFR时,4种方法的评价指标。可以看出,与低混响条件相比,高混响条件下各方法的再现准确度均有一定程度的下降,但各方法的再现准确度和系统稳定性特性仍与低混响条件下的类似,即GSO-GL方法依旧具有较高的再现准确度和系统稳定性,表现出了较强的抗混响能力。
 |
图4 高混响条件下不同布局方法的评价指标 |
4.3 GSO方法所选次级声源个数对再现性能的影响
GSO-GL方法需要先使用GSO方法选择一定数目的次级声源,本小节研究该数目对SFR性能的影响。图 5给出了使用GSO方法选择19, 15, 10个次级声源,再使用组Lasso方法从中选择6个激励声源的SFR结果。由图可得,随着GSO方法所选次级声源个数的减少,系统稳定性指标随之提升,再现准确度指标随之下降且在整个频带内的波动加剧,即GSO方法的特性越明显。因此在使用GSO-GL方法时,可使用GSO选择更少的次级声源以获得更好的系统稳定性指标,也可使用GSO选择更多的次级声源以获得更好的再现准确度指标。GSO-GL方法很好地利用GSO方法所选次级声源个数实现系统稳定性与再现准确度的折中。
 |
图5 使用GSO方法选择19, 15, 10个次级声源的评价指标 |
5 结论
本文提出联合GSO与组Lasso两步的GSO-GL方法,该方法旨在兼顾GSO方法的高系统稳定性与组Lasso方法的高再现准确度,并可通过调节GSO方法选取次级声源个数实现系统稳定性与再现准确度的折中。其中组Lasso方法是一种基于匹配法的宽带SFR方法,其在代价函数中引入了组间稀疏性,通过调节β值控制稀疏性以调节激励声源个数,实现次级声源布局优化。针对二维房间模型中的SFR,研究了GSO-GL方法与组Lasso方法的再现精度和系统稳定性,并与GSO方法和SA算法的性能进行了比较。仿真结果表明,组Lasso方法具有较高的再现精度但系统稳定性稍差,而GSO-GL方法综合了GSO方法的高系统稳定性和组Lasso方法的高再现准确度,在高混响环境中性能依旧良好;在实际工程应用中,该联合方法可在保证高系统稳定性和高再现准确度的条件下,有效减少次级声源个数,降低再现系统实现成本。
References
- LEE J, CHOI J, KIM Y. Reproduction of a higher-order circular harmonic field using a linear array of loudspeakers[J]. Journal of the Acoustical Society of America, 2015, 137(3): 227–233 [Article] [Google Scholar]
- BERKHOUT A J, DE VRIES D, VOGEL P. Acoustic control by wave field synthesis[J]. Journal of the Acoustical Society of America, 1993, 93(5): 2764–2778 [Article] [CrossRef] [Google Scholar]
- POLETTI M A. Three-dimensional surround sound systems based on spherical harmonics[J]. Journal of the Audio Engineering Society, 2005, 53(11): 1004–1025 [Google Scholar]
- KIRKEBY O, NELSON P A, ORDUNA-BUSTAMANTE F, et al. Local sound field reproduction using digital signal processing[J]. Journal of the Acoustical Society of America, 1996, 100(3): 1584–1593 [Article] [CrossRef] [Google Scholar]
- GAUTHIER P A, CAMIER C, LEBEL F A. Experiments of multichannel least-square methods for sound field reproduction inside aircraft mock-up: objective evaluations[J]. Journal of Sound and Vibration, 2016, 376: 194–216 [Article] [CrossRef] [Google Scholar]
- DIAMANTIS Z G, TSAHALIS D T. Optimization of an active noise control system inside an aircraft, based on the simultaneous optimal positioning of microphones and speakers, with the use of a genetic algorithm[J]. Computational Optimization and Applications, 23(1): 65–76 [Article] [Google Scholar]
- BAEK K, ELLIOTT S J. Natural algorithms for choosing source locations in active control systems[J]. Journal of Sound and Vibration, 1995, 186(2): 245–267 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- ASANO F, SUZUKI Y, SWANSON D. Optimization of control source configuration in active control systems using gram-schmidt orthogonalization[J]. IEEE Trans on Speech and Audio Processing, 1999, 7(2): 213–220 [Article] [CrossRef] [Google Scholar]
- LILIS G, ANGELOSANTE D, GIANNAKIS G. Sound field reproduction using the lasso[J], IEEE/ACM Trans on Audio, Speech and Language Processing, 2010, 18(8): 1902–1912 [Article] [Google Scholar]
- MONTAZERI A, POSHTAN J, KAHAEI M H. Optimal placement of loudspeakers and microphones in an enclosure using genetic algorithm[C]//IEEE Conference on Control Applications, 2003: 135–139 [Google Scholar]
- RADMANESH N, BURNETT I S. Generation of isolated wideband sound fields using a combined two-stage lasso-ls algorithm[J]. IEEE Trans on Audio, Speech, and Language Processing, 2013, 21(2): 378–387 [Article] [CrossRef] [Google Scholar]
- YUAN M, LIN Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2006, 68(1): 49–67 [Article] [CrossRef] [Google Scholar]
- GAUTHIER P A, LECOMTE P, BERRY A. Source sparsity control of sound field reproduction using the elastic-net and the lasso minimizers[J]. Journal of the Acoustical Society of America, 2017, 141(4): 2315–2326 [NASA ADS] [CrossRef] [Google Scholar]
- KOYOMA K, CHARDON G, DAUDET L. Optimizing source and sensor placement for sound field control: an overview[J]. IEEE/ACM Trans on Audio, Speech, and Language Processing, 2020, 28: 696–714 [Article] [Google Scholar]
All Figures
 |
图1 GSO-GL方法优化布局流程 |
| In the text | |
 |
图2 二维SFR房间模型 |
| In the text | |
 |
图3 低混响条件下不同布局方法的评价指标 |
| In the text | |
 |
图4 高混响条件下不同布局方法的评价指标 |
| In the text | |
 |
图5 使用GSO方法选择19, 15, 10个次级声源的评价指标 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


