| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 1 - 10 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210001 | |
| Published online | 29 March 2024 | |
Search domain dimension expansion of robust matched-field source radiated power estimation
搜索域维度扩展稳健匹配场声源辐射功率估计
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
2
Shaanxi Key Laboratory of Underwater Information Technology, Xi’an 710072, China
3
Qingdao Research Institute of Northwestern Polytechnical University, Qingdao 266200, China
Received:
22
February
2023
Compared with the traditional source radiated power estimation method, the matched-field source radiated power estimation method can obtain more accurate estimation results. However, its performance is greatly influenced by environmental mismatch. This paper defines the impact factor of environmental mismatch to quantify the impact of environmental mismatch on the acoustic transfer function and the matched-field source radiated power estimation method. It determines that the key to improve the robustness of environmental mismatch is to accurately estimate the acoustic transfer function. In the traditional matched-field source radiated power estimation method, the search domain of the acoustic transfer function is a distance-depth two-dimensional plane and does not contain the true acoustic transfer function when the environment is mismatched. Therefore, the estimation results of the acoustic transfer function are bound to deviate from those of the true acoustic transfer function. The paper expands the search domain dimension to a three-dimensional search domain that contains distance, depth and uncertain parameter sets. The true acoustic transfer function is included in the search domain. Thus the optimal alternative acoustic transfer function is equal to the true acoustic transfer function. The objective function for the three-dimensional search domain is constructed. The smaller the absolute value of the objective function, the less the acoustic transfer function estimation deviates from the true acoustic transfer function. The source radiated power is estimated more accurately when the alternative acoustic transfer function estimation corresponding to the minimum absolute value of the objective function. The simulation results verify the theoretical analysis results.
摘要
与传统声源辐射功率估计方法相比, 匹配场声源辐射功率估计方法能获得更准确的估计结果, 但环境失配对其性能影响较大。针对这一问题, 提出一种搜索域维度扩展稳健匹配场声源辐射功率估计方法。定义环境失配影响因子, 量化表示环境失配对信道传递函数和匹配场声源辐射功率估计方法的影响, 确定提升环境失配稳健性的关键在于准确估计信道传递函数。传统匹配场声源辐射功率估计方法中信道传递函数搜索域是一个距离-深度二维平面, 环境失配时, 其中必然不包含真实信道传递函数, 因此信道传递函数估计结果与真实信道传递函数也必然存在偏差。文中提出的搜索域维度扩展稳健匹配场声源辐射功率估计方法将信道传递函数搜索域扩展为距离、深度和不确定参数组构成的三维搜索空间, 将真实信道传递函数包含在搜索域中, 使得最优备选信道传递函数等于真实信道传递函数。随后构造三维搜索空间的目标函数, 目标函数的绝对值越小, 备选信道传递函数与真实信道传递函数偏差越小。使用目标函数绝对值取最小值时对应的备选信道传递函数可以更准确地估计声源辐射功率, 仿真验证了理论分析的结果。
Key words: source radiated power estimation / search domain dimension expansion / environmental mismatch / robustness
关键字 : 声源辐射功率估计 / 搜索域维度扩展 / 环境失配 / 稳健性
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
声源辐射功率谱密度(power spectral density, PSD)是辐射声源的一种基本物理特征, 不随所处海洋环境和接收平台变化而变化。PSD给出了各频点处的声源辐射功率, 使用PSD可以计算得到总声源级(source level, SL)和声源频带级(source band level, SBL)等其他描述声源辐射功率特征的物理量[1]。声源辐射PSD估计问题通常在频域进行研究, 可以通过逐一估计各个频点的声源辐射功率得到声源辐射PSD, 因此声源辐射PSD估计问题可转化为确定频点上的声源辐射功率估计问题。一般通过接收数据得到接收信号功率, 再补偿传播损失得到声源辐射功率, 接收信号功率和传播损失的准确性直接影响声源辐射功率估计结果的准确性。由于使用方便和成本较低, 早期声源辐射功率估计方法主要使用单水听器[2-3]。估计安静型目标的辐射功率时, 使用单水听器的接收信噪比(signal-to-noise ratio, SNR)较低, 接收信号功率估计结果偏差较大。因此, 后续声源辐射功率估计方法逐渐使用垂直阵[4-5]替代单水听器接收信号。传统声源辐射功率估计方法研究在平面波声传播假设下进行, 与实际浅海波导环境不符, 导致在实际应用时声源辐射功率估计性能下降。针对这一问题, 向龙凤等提出了匹配场声源辐射功率估计方法[6] (matched-field source radiated power estimation, MFPE)。MFPE方法假设环境参数确定已知, 使用根据简正波声场模型得到的信道传递函数描述声传播过程。实际接收信号功率即为声源位置处的Bartlett匹配场波束输出, 实际声传播损失可由信道传递函数模值精确计算得到。相应地, 声源辐射功率估计性能较好。然而, 实际应用时环境参数通常是不确定的[7-10], 由此带来的环境失配问题不可避免地影响声源辐射功率的估计精度。
稳健匹配场声源辐射功率估计方法的目的是在环境失配时尽可能获得准确的声源辐射功率估计结果。研究表明[11], 环境失配时, 提升声源辐射功率估计结果精度的关键在于降低信道传递函数估计结果与真实信道传递函数的偏差。现有关于稳健匹配场声源辐射功率估计方法的研究很少, 而关于稳健定位方法的研究相对较多[12-13]。其中, 提升MVDR匹配场定位方法(minimum variance distortionless response matched field processing, MVDR-MFP)的环境失配稳健性时, 一般默认常规匹配场定位方法的环境失配稳健性较高, 通过对角加载[14]、临点位置约束[15]、环境扰动约束[16]或者特征值提取[17-18]等方法构造MVDR-MFP的权值, 使得MVDR-MFP在环境失配时尽可能获得常规匹配场定位方法的环境失配稳健性。这些稳健MVDR-MFP方法不涉及信道传递函数的稳健估计, 对本文研究参考价值较低。稳健定位方法的目的是在环境失配时尽可能获得准确的声源位置估计结果, 不确定环境参数的准确性不是稳健定位方法关心的内容。由于许多定位方法没有考虑环境参数不确定先验信息, 即使声源位置信息能够准确获得, 环境参数的不确定性仍会导致信道传递函数估计结果与真实信道传递函数存在偏差。Collins和Kuperman提出的参数聚焦定位方法[19]扩展参数搜索域, 将所有不确定参数考虑进来, 同时估计声源位置参数和环境参数。通过利用所有环境不确定先验信息, 参数聚焦定位方法有效改善了环境失配时的定位效果。另外, 由于参数聚焦定位方法可以同时获得较为准确的声源位置参数估计结果和环境参数估计结果, 获得与真实信道传递函数偏差较小的信道传递函数估计结果成为可能。本文将这一思路应用到声源辐射功率估计问题中, 提出一种搜索域维度扩展稳健匹配场声源功率估计方法(search domain dimension expansion of robust matched-field source radiated power estimation, DE-MFPE)。
本文首先介绍MFPE方法并分析性能; 随后分析环境失配时MFPE方法的误差来源, 定义环境失配影响因子量化表示环境失配对信道传递函数和MFPE方法的影响; 随后引入参数不确定范围, 并扩展信道传递函数搜索域维度, 定性分析扩展搜索域维度能提升环境失配稳健性的原因; 随后构造目标函数用来搜索最优备选信道传递函数, 通过推导目标函数与环境失配影响因子的关系, 指出使用搜索域维度扩展稳健匹配场声源功率估计方法需要满足的条件。最后使用Benchmark浅海波导不确定环境模型[20]仿真验证理论分析的结果。
1 匹配场声源辐射功率估计方法
1.1 接收信号模型
在任一确定频点处, 建立接收信号频域模型。假设声源深度为zs, 使用N元垂直线列阵接收信号, 声源到垂直阵的水平距离为r。接收信号频域快拍 X可表示为
式中:a为声源辐射信号频谱幅度, 是一个确定但未知的量; n为接收基阵上的背景噪声构成的N×1维向量, 假设背景噪声为加性高斯白噪声, 各阵元上的噪声功率相等为σn2; Φ为浅海波导环境参数向量; H(r, zs, Φ)是声源到各接收阵元的信道传递函数构成的N×1维向量
式中:Gi(r, zs, Φ)为声源到第i个接收阵元的信道传递函数, 给出了声源辐射信号在浅海波导传播过程中的相位变化和能量损失, i=1, 2, ⋯, N。事实上, H(r, zs, Φ)是未知的, 只能假定或估计r, zs和 Φ等先验信息, 再根据声场模型理论计算得到 H(r, zs, Φ)的估计结果。将假定或估计的先验信息记为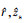 和
和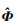 , 对应的信道传递函数估计结果记为
, 对应的信道传递函数估计结果记为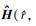
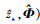 。
。
1.2 声源辐射功率估计
MFPE方法假设环境参数先验信息已知, 即 。在该假设下, 声源位置先验信息可通过匹配场定位方法准确获得, 即
。在该假设下, 声源位置先验信息可通过匹配场定位方法准确获得, 即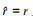 且
且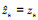 。此时, 信道传递函数估计结果等于真实信道传递函数, 即
。此时, 信道传递函数估计结果等于真实信道传递函数, 即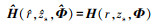 。MFPE方法给出a的达到克拉美罗下限的最小方差无偏估计为
。MFPE方法给出a的达到克拉美罗下限的最小方差无偏估计为
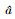 的期望和方差为
的期望和方差为
声源辐射功率估计值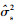 为
为
(4) 式中, R = XXH。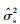 的数学期望为
的数学期望为
(5) 式中
符号“‖‖”2表示二范数; a2为声源辐射功率, ‖ H (r, zs, Φ)‖22表示声传播损失, 则a2‖ H(r, zs, Φ)‖22为阵列接收信号功率, (6)式给出阵列接收信噪比。
由(5)式可以看出: 环境已知时, MFPE方法的声源辐射功率估计值是有偏的, 声源辐射功率估计值的偏差只与信噪比RSN有关; 当RSN→+∞时,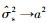 , 即声源辐射功率估计值等于真实信号辐射功率。
, 即声源辐射功率估计值等于真实信号辐射功率。
2 搜索域维度扩展稳健匹配场声源辐射功率估计方法
实际使用时, 环境参数先验信息通常是失配的, 即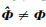 。受环境失配影响, 声源位置估计结果也存在偏差, 即
。受环境失配影响, 声源位置估计结果也存在偏差, 即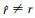 或
或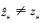 。先验信息的失配导致信道传递函数估计结果与真实信道传递函数存在偏差, 即
。先验信息的失配导致信道传递函数估计结果与真实信道传递函数存在偏差, 即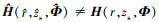 。使用
。使用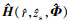 计算声源辐射功率估计值, 分析环境失配时MFPE方法的误差来源。
计算声源辐射功率估计值, 分析环境失配时MFPE方法的误差来源。
2.1 环境失配影响因子
将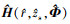 代入(4)式, 并将计算结果表示为对数形式
代入(4)式, 并将计算结果表示为对数形式
将(1)式代入(7)式, 并做等价数学变换可得
式中
从(8)式可以看出, MFPE方法误差来源有2个, 分别是环境失配和环境噪声。环境失配主要通过影响信道传递函数影响MFPE方法的性能, Δe量化了环境失配时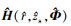 与H(r, zs, Φ)的偏差程度, 也量化了环境失配对声源辐射功率估计结果的影响, 本文将Δe称作环境失配影响因子。丨Δe丨越大, 环境失配对信道传递函数的影响越大, 声源辐射功率估计值的误差越大。Δn量化了环境噪声对声源辐射功率估计结果的影响, 本文将Δn称作环境噪声影响因子。Δn与RSN有关, RSN越大, Δn越小。
与H(r, zs, Φ)的偏差程度, 也量化了环境失配对声源辐射功率估计结果的影响, 本文将Δe称作环境失配影响因子。丨Δe丨越大, 环境失配对信道传递函数的影响越大, 声源辐射功率估计值的误差越大。Δn量化了环境噪声对声源辐射功率估计结果的影响, 本文将Δn称作环境噪声影响因子。Δn与RSN有关, RSN越大, Δn越小。
Δe与环境失配程度密切相关, 与RSN无关, 始终影响MFPE方法的声源辐射功率估计性能, Δe的大小直接反映了环境失配稳健性的高低。由(9)式可知, 当且仅当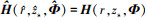 时, 丨Δe丨取最小值0。可见, 为获得 H(r, zs, Φ), 只需在信道传递函数搜索域内搜索使丨Δe丨达到最小值的备选信道传递函数即可。首先需要选择合适的信道传递函数搜索域, 由于信道传递函数是r, zs和 Φ的函数, 信道传递函数搜索域可通过参数不确定范围得到。
时, 丨Δe丨取最小值0。可见, 为获得 H(r, zs, Φ), 只需在信道传递函数搜索域内搜索使丨Δe丨达到最小值的备选信道传递函数即可。首先需要选择合适的信道传递函数搜索域, 由于信道传递函数是r, zs和 Φ的函数, 信道传递函数搜索域可通过参数不确定范围得到。
2.2 参数不确定范围
环境失配时, 虽然无法准确获知r, zs和 Φ, 但是r, zs和 Φ的不确定范围容易获得。将r和zs的不确定范围分别写为
式中: Ur和 Uz分别为表示r和zs不确定范围的集合; rmin和rmax为研究海域中声源到垂直阵水平距离的最小值和最大值, zmin和zmax为研究海域中声源深度的最小值和最大值。Benchmark浅海波导不确定环境模型[20]是由美国海军实验室在大量实测数据的基础上提供的, 其中包括各环境参数的不确定范围, 如图 1所示。该模型在浅海波导环境不确定性问题的研究中应用广泛, 本文研究也使用该环境参数不确定模型。图中给出了不确定环境参数的符号及其不确定范围, 其中声速剖面的不确定范围由黑色虚线表示。不确定环境参数种类有7个, 分别为海水深度dw、海水上表面声速c1、海水下表面声速c2、沉积层上表面声速c3、沉积层下表面声速c4、沉积层吸收系数α和沉积层密度ρ。则 Φ可以写为
Φ的不确定范围为
实际海洋环境参数可能是UΦ内任意一组环境参数。实际应用时通常根据经验或现有的水文数据假设一组环境参数值 Φ0, 本文假设 Φ0为参数不确定范围的中值
Φ在图 1中由黑色实线表示。使用(11)~(12)式和(14)式给出的参数不确定范围先验信息, 选择合适的信道传递函数搜索域。
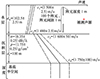 |
图1 Benchmark浅海波导不确定环境模型 |
2.3 搜索域维度扩展
MFPE方法没有考虑环境参数不确定范围, 仅在Ur和 Uz2个维度上搜索, 对应的信道传递函数搜索域是一个距离-深度二维搜索平面, 可写为
式中: H表示信道传递函数搜索域; 下标“2”表示搜索域维度。
图 2给出了环境已知和环境失配时MFPE方法的信道传递函数搜索域示意图, 将 H (r, zs, Φ)所在距离-深度二维平面记为平面A, 图中红色五角星表示真实声源位置对应的备选信道传递函数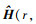
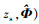 。环境已知时,
。环境已知时,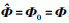 , MFPE方法的信道传递函数搜索域与平面A完全重合。真实声源位置对应的备选信道传递函数
, MFPE方法的信道传递函数搜索域与平面A完全重合。真实声源位置对应的备选信道传递函数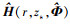 =H(r, zs, Φ), 丨Δe丨达到理论最小值0的最优备选信道传递函数。环境失配时,
=H(r, zs, Φ), 丨Δe丨达到理论最小值0的最优备选信道传递函数。环境失配时,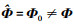 , 将MFPE方法的信道传递函数搜索域记为平面B。将丨Δe丨的最小值对应的最优备选信道传递函数记为
, 将MFPE方法的信道传递函数搜索域记为平面B。将丨Δe丨的最小值对应的最优备选信道传递函数记为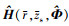 , 在图中用红色圆圈表示。由于平面A与平面B没有交集, 在现有信道传递函数搜索域内不可能获得 H(r, zs, Φ),
, 在图中用红色圆圈表示。由于平面A与平面B没有交集, 在现有信道传递函数搜索域内不可能获得 H(r, zs, Φ),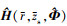 必然与 H(r, zs, Φ)存在偏差, 声源辐射功率估计结果也必然存在误差。可见, 环境失配时仅搜索距离-深度二维平面是不够的, 需要考虑环境参数不确定范围, 进行搜索域维度扩展。
必然与 H(r, zs, Φ)存在偏差, 声源辐射功率估计结果也必然存在误差。可见, 环境失配时仅搜索距离-深度二维平面是不够的, 需要考虑环境参数不确定范围, 进行搜索域维度扩展。
引入环境参数不确定范围UΦ, 在 Ur, Uz和 UΦ维度上搜索, 对应的信道传递函数搜索域是一个三维搜索空间, 可写为
图 3给出了搜索域维度扩展示意图。维度UΦ中有无穷多组环境参数, 其中包含 Φ。图 3只给出了 H3中Q组不确定环境参数对应的Q个距离-深度二维平面, 记为Bq, q=1, 2, ⋯, Q。通过扩展搜索域维度, H3包含平面A,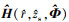 的理论最优解等于 H(r, zs, Φ)。可见, 搜索域维度扩展的意义在于提升了理论最优信道传递函数估计结果与理论最优声源辐射功率估计值的上限。
的理论最优解等于 H(r, zs, Φ)。可见, 搜索域维度扩展的意义在于提升了理论最优信道传递函数估计结果与理论最优声源辐射功率估计值的上限。
然而受计算能力影响, 实际搜索时, 只能通过在距离、深度以及环境参数维度上划分网格, 网格点对应的备选信道传递函数只是信道传递函数搜索域内一小部分备选信道传递函数。当这些离散网格点对应的备选信道传递函数中恰好包含 H(r, zs, Φ)时, 才能获得信道传递函数估计结果和声源辐射功率估计值的理论最优解。提升网格精度并采用遍历搜索是提升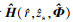 准确性的有效方法, 但计算量很大。在不确定环境参数个数较多时, 本文使用遗传算法等智能全局搜索算法[21-24]降低时间成本。遗传算法对环境失配稳健性的提升没有贡献, 甚至受遗传算法计算能力的限制, 获得的
准确性的有效方法, 但计算量很大。在不确定环境参数个数较多时, 本文使用遗传算法等智能全局搜索算法[21-24]降低时间成本。遗传算法对环境失配稳健性的提升没有贡献, 甚至受遗传算法计算能力的限制, 获得的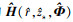 不够准确[24], 信道传递函数估计结果和声源辐射功率估计结果的误差可能会增大。
不够准确[24], 信道传递函数估计结果和声源辐射功率估计结果的误差可能会增大。
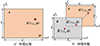 |
图2 MFPE的信道传递函数搜索域示意图 |
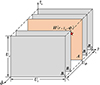 |
图3 搜索域维度扩展示意图 |
2.4 声源辐射功率估计
由2.1节可知, 可以将环境失配影响因子丨Δe丨作为目标函数, 在H3中搜索使丨Δe丨达到最小值的信道传递函数, 用来估计声源辐射功率。由于(9)式中 H(r, zs, Φ)是未知的, 实际应用时只有接收信号频域快拍X可以使用, 因此使用X构造目标函数为
则信道传递函数估计问题可写为
将搜索得到的信道传递函数估计结果记为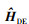 , 下标“DE”表示DE-MFPE方法。将
, 下标“DE”表示DE-MFPE方法。将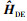 代入(4)式可得声源辐射功率估计值
代入(4)式可得声源辐射功率估计值
当RSN足够大时, X ≈ H (r, zs, Φ)a。目标函数可以写为
式中,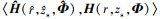 为
为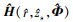 和 H (r, zs, Φ)的夹角。由(21)式可知, 当且仅当
和 H (r, zs, Φ)的夹角。由(21)式可知, 当且仅当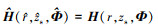 时, 目标函数取最大值。信道传递函数估计结果与真实信道传递函数之间偏差很小, 声源辐射功率估计性能很好。
时, 目标函数取最大值。信道传递函数估计结果与真实信道传递函数之间偏差很小, 声源辐射功率估计性能很好。
3 数值仿真分析
仿真使用图 1给出的Benchmark浅海波导声速剖面, 假设环境参数在参数不确定范围内服从均匀分布, 信道传递函数计算使用简正波声场模型。仿真使用阵元间距为1 m的100元均匀垂直线列阵接收信号。假设声源到接收基阵的距离变化范围为1~1 000 m, 声源深度变化范围为1~100 m。声源辐射信号一般为宽带, 假设信号频率范围为100~1 000 Hz。假设频段内环境噪声为60 dB并保持不变, 通过改变声源辐射功率标称值改变接收信噪比RSN。仿真中采用的蒙特卡罗仿真次数均为1 000。
3.1 不同环境参数失配对匹配场声源辐射功率估计方法的影响程度
本文考虑的不确定环境包含7个环境参数, 加上2个声源位置参数, 共9个不确定参数。假设每个不确定参数的离散点个数为β, 则共有β9个离散点需要搜索。可见, 信道传递函数搜索空间的离散点个数随不确定参数个数增长呈指数增长趋势。受硬件设施计算能力的限制, 很难在保证搜索精度的同时遍历每一个离散点。为验证DE-MFPE方法的声源辐射功率估计值的环境失配稳健性, 本文考虑先假设除声源位置参数外, 失配的环境参数只有一个, 使得需要搜索的离散点个数在硬件设施计算能力的可承受范围内。随后考虑7个环境参数同时失配, 使用遗传算法搜索信道传递函数, 并对比分析信道传递函数搜索方法对DE-MFPE方法性能的限制。
采用控制变量法分析不同环境参数单独失配时, 环境失配影响因子的大小。图 4给出了不同环境参数失配时, MFPE方法的环境失配影响因子随信号频率的变化。可以看出, 海水深度变化时的丨Δe丨远大于其他环境参数变化时的丨Δe丨。说明海水深度变化对信道传递函数的影响非常严重, 海水深度变化给MFPE方法的声源辐射功率估计结果带来的误差最高可达6.9 dB。相对地, 其他环境参数变化对信道传递函数的影响很小, 给MFPE方法的声源辐射功率估计结果带来的误差不超过1 dB。因此, 假设只有一个环境参数失配时, 考虑除声源位置参数外, 只有海水深度失配。
 |
图4 不同环境参数失配时环境失配影响因子随信号频率的变化 |
3.2 声源辐射功率估计性能随信噪比的变化
假设只有海水深度失配, 声源辐射功率标称值变化范围为80~140 dB, 对应阵列接收RSN变化范围为-7.8~52.2 dB。图 5分别给出了MFPE方法和DE-MFPE方法的Δn随RSN的变化。图中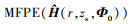 为使用
为使用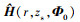 时MFPE方法的Δn随RSN的变化曲线, 此时MFPE对RSN的要求最高;
时MFPE方法的Δn随RSN的变化曲线, 此时MFPE对RSN的要求最高;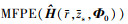 为使用
为使用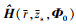 时MFPE方法的Δn随RSN的变化曲线, 是环境失配时MFPE方法的最优性能, 对RSN的要求也更低; DE-MFPE方法对RSN的要求最低, 逼近环境已知时MFPE方法对信噪比的要求。信噪比大于26.13 dB, 即声源辐射功率标称值大于114 dB时, 环境噪声给不同声源辐射功率估计方法带来的误差均小于1 dB。
时MFPE方法的Δn随RSN的变化曲线, 是环境失配时MFPE方法的最优性能, 对RSN的要求也更低; DE-MFPE方法对RSN的要求最低, 逼近环境已知时MFPE方法对信噪比的要求。信噪比大于26.13 dB, 即声源辐射功率标称值大于114 dB时, 环境噪声给不同声源辐射功率估计方法带来的误差均小于1 dB。
 |
图5 MFPE和DE-MFPE的Δn随RSN的变化 |
3.3 声源辐射功率估计性能随信号频率的变化
假设声源辐射功率标称值为120 dB, 此时声源辐射功率估计结果的误差主要来源于环境失配。假设声源深度50 m, 声源到接收基阵的距离为500 m, 图 6给出了MFPE方法和DE-MFPE方法的声源辐射功率估计性能随信号频率的变化。由于环境噪声功率估计性能随信号频率的变化对声源辐射功率估计结果的影响很小, 丨Δe丨和声源辐射功率估计结果的误差随信号频率的变化趋势基本一致, 均随信号频率增大而增大; 环境失配使得声源辐射功率估计值小于标称值。使用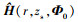 的MFPE方法的声源辐射功率估计误差很大, 随信号频率的增长速度最快; 使用
的MFPE方法的声源辐射功率估计误差很大, 随信号频率的增长速度最快; 使用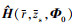 的MFPE方法的声源辐射功率估计误差较小, 随信号频率的增长速度较慢。可见, 使用距离-深度二维信道传递函数搜索平面, 最优声源辐射功率估计值的误差仍然较大。信号频率1 000 Hz时, 最优声源辐射功率估计值的误差约为1.72 dB。DE-MFPE方法在三维空间搜索信道传递函数, 声源辐射功率估计误差最小, 随信号频率的增长速度最慢, 信号频率1 000 Hz时, 声源辐射功率估计误差仅为0.23 dB。可见, 扩展信道传递函数搜索域维度有效提升了声源辐射功率估计性能上限。
的MFPE方法的声源辐射功率估计误差较小, 随信号频率的增长速度较慢。可见, 使用距离-深度二维信道传递函数搜索平面, 最优声源辐射功率估计值的误差仍然较大。信号频率1 000 Hz时, 最优声源辐射功率估计值的误差约为1.72 dB。DE-MFPE方法在三维空间搜索信道传递函数, 声源辐射功率估计误差最小, 随信号频率的增长速度最慢, 信号频率1 000 Hz时, 声源辐射功率估计误差仅为0.23 dB。可见, 扩展信道传递函数搜索域维度有效提升了声源辐射功率估计性能上限。
 |
图6 MFPE和DE-MFPE的声源辐射功率估计性能随信号频率的变化 |
3.4 声源辐射功率估计性能随声源位置的变化
假设信号频率为500 Hz, 声源辐射功率标称值为120 dB, 改变声源位置, 图 7给出了MFPE方法和DE-MFPE方法的声源辐射功率估计结果随声源位置的变化。从图中可以得到类似的规律: 声源在不同位置时, 环境失配对MFPE方法的影响很大。MFPE方法的最优声源辐射功率估计结果的误差仍然较大; 在本文研究仿真环境下, 声源辐射功率估计结果的误差可达2 dB。DE-MFPE方法的声源辐射功率估计性能很好, 声源在不同位置时, 声源辐射功率估计的误差几乎为0。
 |
图7 MFPE和DE-MFPE的声源辐射功率估计结果随声源位置的变化 |
3.5 信道传递函数搜索方法对DE-MFPE方法性能的限制
考虑9个参数均不确定, 此时信道传递函数搜索域内需要搜索的离散点过多, 需要使用遗传算法搜索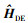 。每个不确定参数采用12位二进制编码, 交叉概率位0.8, 变异概率为0.05, 种群中个体为100个, 种群迭代200次之后停止迭代, 输出
。每个不确定参数采用12位二进制编码, 交叉概率位0.8, 变异概率为0.05, 种群中个体为100个, 种群迭代200次之后停止迭代, 输出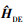 。由于搜索方法的性能限制,
。由于搜索方法的性能限制,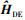 与真实信道传递函数的差异增大, DE-MFPE方法的环境失配稳健性也随之降低。图 8给出了9个参数均不确定时, MFPE方法和DE-MFPE方法的声源辐射功率估计结果。当声源辐射功率标称值较小时, 接收信噪比也较小。此时, 目标函数无法看作环境失配影响因子, DE-MFPE方法的声源辐射功率估计误差很大, MFPE方法的声源辐射功率估计误差也很大。当声源辐射功率标称值大于100 dB时, 对应阵列接收信噪比大于12.2 dB。此时, MFPE方法的声源辐射功率估计误差约为1.3 dB, DE-MFPE方法的声源辐射功率估计误差小于1 dB。可见, DE-MFPE方法的声源辐射功率估计性能下降, 但仍略优于MFPE方法。改变信号频率和声源位置也能得到类似的结论, 此处不再赘述。
与真实信道传递函数的差异增大, DE-MFPE方法的环境失配稳健性也随之降低。图 8给出了9个参数均不确定时, MFPE方法和DE-MFPE方法的声源辐射功率估计结果。当声源辐射功率标称值较小时, 接收信噪比也较小。此时, 目标函数无法看作环境失配影响因子, DE-MFPE方法的声源辐射功率估计误差很大, MFPE方法的声源辐射功率估计误差也很大。当声源辐射功率标称值大于100 dB时, 对应阵列接收信噪比大于12.2 dB。此时, MFPE方法的声源辐射功率估计误差约为1.3 dB, DE-MFPE方法的声源辐射功率估计误差小于1 dB。可见, DE-MFPE方法的声源辐射功率估计性能下降, 但仍略优于MFPE方法。改变信号频率和声源位置也能得到类似的结论, 此处不再赘述。
 |
图8 MFPE和DE-MFPE的声源辐射功率估计结果 |
4 结论
本文针对环境失配时匹配场声源辐射功率估计方法受环境失配影响较大的问题, 提出一种搜索域维度扩展稳健匹配场声源辐射功率估计方法。分析了环境失配时匹配场声源辐射功率估计方法的误差来源, 定义环境失配影响因子量化环境失配对信道传递函数的影响。通过分析环境失配影响因子可知, 准确估计信道传递函数是提升环境失配稳健性的关键, 而真实信道传递函数可通过搜索使环境失配影响因子最小的备选信道传递函数得到。分析环境失配前后匹配场声源辐射功率估计方法的信道传递函数搜索域, 发现环境失配时距离-深度二维搜索平面内不包含真实信道传递函数, 因此无法通过优化环境失配影响因子准确估计信道传递函数。针对这一问题, 搜索域维度扩展稳健匹配场声源辐射功率估计方法将不确定参数的不确定范围考虑进来, 将信道传递函数搜索域扩展为距离-深度-不确定参数三维搜索空间, 其中包含真实信道传递函数。由于环境失配影响因子无法直接获得, 本文给出了可用来替代环境失配影响因子的目标函数。环境失配时, 搜索域维度扩展稳健匹配场声源辐射功率估计方法可以通过在信道传递函数搜索域内对目标函数寻优准确估计信道传递函数, 从而提高环境失配稳健性。不确定环境参数较少时, 搜索域维度扩展稳健匹配场声源辐射功率估计方法的性能很好, 声源辐射功率估计结果的环境失配稳健性很高。不确定环境参数较多时, 由于可以使用的搜索算法的计算能力不足, 搜索域维度扩展稳健匹配场声源辐射功率估计方法的实际使用性能会略低于理论最优性能; 仿真结果表明, 受搜索算法性能限制的情况下, 搜索域维度扩展稳健匹配场声源辐射功率估计方法的环境失配稳健性仍优于匹配场声源辐射功率估计方法。
References
- JIANG Guoqing, SUN Chao, LIU Xionghou, et al. Radiated noise measurement by a small-aperture vertical array based on robust principal component analysis[J]. Journal of Harbin Engineering University, 2020, 41(10): 1493–1499 [Article] (in Chinese) [Google Scholar]
- GAO Yuan, SHI Shengguo. Method and design of measuring the radiated noise using vertical array in the shallow sea[J]. Technical Acoustics, 2010, 29(6): 80–82 (in Chinese) [Google Scholar]
- FANG Erzheng, YANG Desen. Research on an acoustic measurement array for underwater target of low radiated noise based on vector hydrophone[J]. Technical Acoustics, 2009, 28(2): 91–92 [Article] (in Chinese) [Google Scholar]
- WU Guoqing, WANG Meigang, CHEN Shouhu, et al. Error analysis and correction method of underwater vessel radiated noise measurement by vertical array and signal hydrophone[J]. Acta Acoustic, 2007, 32(5): 398–403 [Article] (in Chinese) [Google Scholar]
- SUN Guiqing, YANG Desen, ZHANG Lanyue, et al. Research on the method for measuring radiated noise by an underwater target in low frequency band based on the vector hydrophone[J]. Acta Acoustic, 2002, 27(5): 429–434 [Article] (in Chinese) [Google Scholar]
- XIANG Longfeng, SUN Chao. An estimation method of ship radiated noise level based on matched field processing[J]. Acta Acoustic, 2014, 39(5): 570–576 [Article] (in Chinese) [Google Scholar]
- SHANG E C, WANG Y Y. Environmental mismatching effects on source localization processing in mode space[J]. Journal of the Acoustical Society of America, 1991, 89(5): 2285–2290 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- HAMSON R M, HEITMEYER R M. Environmental and system effects on source localization in shallow water by the matched-field processing of a vertical array[J]. Journal of the Acoustical Society of America, 1989, 86(5): 1950–1959 [Article] [CrossRef] [Google Scholar]
- FEUILLADE C, DEL BALZO D R, Rowe M M. Environmental mismatch in shallow-water matched-field processing: geoacou-stic parameter variability[J]. Journal of the Acoustical Society of America, 1989 85(6): 2354–2364 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- LIU Zongwei, SUN Chao, DU Jinyan. The measure of environmental sensitivity in detection performance degradation[J]. Acta Physica Siniccl, 2013, 62(6): 064303 [Article] (in Chinese) [CrossRef] [Google Scholar]
- ZHANG Shaodong, SUN Chao, XIE Lei, et al. Influence of environmental uncertainty on source power estimation in shallow water waveguide[J]. Acta Physica Siniccl, 2013, 70(24): 244301[Article] (in Chinese) [CrossRef] [Google Scholar]
- YANG Kunde, MA Yuanliang, ZOU Shixin, et al. Linear matched field processing based on environmental perturbation[J]. Acta Acoustic, 2006, 31(6): 496–505 [Article] (in Chinese) [Google Scholar]
- GINGRAS D F, GERR N L. Minimax robust matched-field processing[J]. Journal of the Acoustical Society of America, 1993, 93(5): 2798–2808 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- YANG Kunde, MA Yuanliang. Robust adaptive matched field processing with sector eigenvector constraints[J]. Acta Acoustic, 2006, 31(5): 400–409 [Article] (in Chinese) [Google Scholar]
- SCHMIDT H, BAGGEROER A B, KUPERMAN W A. Environmentally tolerant beamforming for high-resolution matched field processing: deterministic mismatch[J]. Journal of the Acoustical Society of America, 1990, 88(4): 1851–1862 [Article] [CrossRef] [Google Scholar]
- SHOREY J A, NOLTE L W, KROLIK J L. Computationally efficient monte carlo estimation algorithms for matched field processing in uncertain ocean environments[J]. Journal of the Acoustical Society of America, 1994, 2(3): 285–314 [Google Scholar]
- FRICHTER G M, BYRNE C L, FEUILLADE C. Sector-focused stability methods for robust source localization in matched-field processing[J]. Journal of the Acoustical Society of America, 1990, 88(6): 2843–2851 [Article] [CrossRef] [Google Scholar]
- CHANDLER H A, FEUILLADE C, SMITH G B. Sector-focused processing for stabilized resolution of multiple acoustic sources[J]. Journal of the Acoustical Society of America, 1995, 97(4): 2159–2172 [Article] [CrossRef] [Google Scholar]
- COLLINS M D, KUPERMAN W A. Focalization: environmental focusing and source localization[J]. Journal of the Acoustical Society of America, 1991, 90(3): 1410–1422 [Article] [CrossRef] [Google Scholar]
- PORTER M B. The matched field processing benchmark problems[J]. Journal of Computational Acoustics, 1994, 2(3): 161–185 [Article] [CrossRef] [Google Scholar]
- VAZ A I F, VICENTE L N. A particle swarm pattern search method for bound constrained global optimization[J]. Journal of Global Optimization, 2007, 39(2): 197–219 [Article] [CrossRef] [Google Scholar]
- DORIGO M, GAMBARDELLA L M. Ant colonies for the traveling salesman problem[J]. Biosystems, 1997, 43(2): 73–81 [CrossRef] [Google Scholar]
- SAMBRIDGE M, DRIJKONINGEN G. Genetic algorithms in seismic waveform inversion[J]. Geophysical Journal of the Royal Astronomical Society, 1992, 109(2): 323–342 [CrossRef] [Google Scholar]
- ZHANG Shaodong, SUN Chao, WANG Xuan. Estimation of acoustic transfer function by using genetic algorithm[C]//Oceans Conference, Chennai, India, 2022 [Google Scholar]
All Figures
 |
图1 Benchmark浅海波导不确定环境模型 |
| In the text | |
 |
图2 MFPE的信道传递函数搜索域示意图 |
| In the text | |
 |
图3 搜索域维度扩展示意图 |
| In the text | |
 |
图4 不同环境参数失配时环境失配影响因子随信号频率的变化 |
| In the text | |
 |
图5 MFPE和DE-MFPE的Δn随RSN的变化 |
| In the text | |
 |
图6 MFPE和DE-MFPE的声源辐射功率估计性能随信号频率的变化 |
| In the text | |
 |
图7 MFPE和DE-MFPE的声源辐射功率估计结果随声源位置的变化 |
| In the text | |
 |
图8 MFPE和DE-MFPE的声源辐射功率估计结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


