| Issue |
JNWPU
Volume 37, Number 6, December 2019
|
|
|---|---|---|
| Page(s) | 1231 - 1237 | |
| DOI | https://doi.org/10.1051/jnwpu/20193761231 | |
| Published online | 11 February 2020 | |
A New Method of Flutter Boundary Prediction for Progressive Variable Speed Based on EM-KS Algorithm
一种基于EM-KS算法的连续变速颤振边界预测方法
1
School of Power and Energy, Northwestern Polytechnical University, Xi'an 710072, China
2
Shanghai Aircraft Design and Reseavch Institute, Shanghai 201210, China
Received:
8
November
2018
The flutter test with progression variable speed is actively explored in recent years. This paper proposes an improved Kalman smoothing filter (EM-KS) algorithm based on expectation maximization for the non-stationary characteristics of the signal in this type of experiment, which can effectively improve the estimation accuracy of time-varying parameter modeling. Combining with the flutter time domain criterion, a new method for flutter boundary prediction of flutter test with progression variable speed that can be recursively implemented is given. Finally, the reliability and engineering applicability of this method are validated by numerical simulation and measured data. The results show that the flutter boundary prediction method based on EM-KS does not depend on the assumption of stationary stochastic process, and the accuracy can meet the actual engineering needs.
摘要
连续变速颤振试验(FTPVS)是近年来积极探索的一种颤振试验方案。针对该类试验中信号非平稳的特点,创新性地将期望最大化方法迭代优化的思想用于改善连续变速颤振信号的建模精度,提出了一种基于该方法的卡尔曼滤波平滑(EM-KS)算法,有效提高了时变参数的辨识性能。进而结合颤振时域判据,给出了可递推实现的连续变速颤振试验的颤振边界预测方法。最后通过数值仿真和实测数据对所提方法的可靠性与工程适用性进行了验证,结果表明,基于EM-KS颤振边界预测方法不依赖于平稳随机过程的假设,精确度可以满足实际工程需要。
Key words: EM-KS algorithm / Kalman filter smoothing / TVAR / flutter boundary prediction / numerical simulation / flutter time domain criterion
关键字 : EM-KS算法 / 卡尔曼滤波平滑 / TVAR / 颤振边界预测 / /
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
颤振试验是飞行器研制过程中必不可少的环节, 而试验数据分析对于研究颤振品质和保障后续试验安全具有重要的意义[1]。传统的颤振试验是以速度台阶的方式进行的, 其依据是假设在每个台阶内气动力和结构响应都属于平稳随机过程, 从而可以利用频域方法进行模态参数的估计。但这种试验方式不仅周期长、成本高, 且与飞行器实际飞行状态有较大差别。连续变速颤振试验是近年来提出并被积极探索的一种新的试验方式[2], 它允许表速或马赫数连续变化, 使得试验方式更加自由, 成本和周期也急剧降低, 但同时也带来了实测数据非平稳的问题, 造成后续信号分析困难。
围绕着非平稳颤振信号处理, 以自适应滤波为代表的动态数据建模方法逐渐成为了一个研究热点, 然而时变参数模型的估计精度和跟踪性能将直接影响颤振试验分析结论的可靠性。基于状态空间模型的卡尔曼滤波不仅是均方误差意义下的线性最优估计器, 而且在处理非平稳随机信号中具有先天的递推优势。但传统卡尔曼滤波算法存在着收敛性差、参数估计精度不高的问题[3]。
为此, 本文针对连续变速颤振试验中观测信号的非平稳特性, 提出了一种基于期望最大化的卡尔曼滤波平滑(EM-KS)算法。算法以迭代的方式运行, 每次先由卡尔曼滤波器进行状态估计, 随后应用卡尔曼平滑算法(KS)和期望最大化算法(EM)对卡尔曼相关参数矩阵进行优化[4], 保证在下次迭代中提高算法对状态和参数的估计精度, 后续应用颤振时域判据对连续变速颤振试验进行边界预测。仿真和实测数据验证表明, 本文提出的辨识方法可以较准确地跟踪模型时变参数, 保证了颤振时域判据的稳定性, 从而提高了颤振预测的精度, 具有重要的理论研究意义和工程实用价值。
1 卡尔曼滤波及其改进算法
1.1 状态空间模型与时变参数建模
对于连续变速颤振试验的非平稳结构响应信号, 一般可以用时变自回归(TVAR)模型来进行建模
式中, p是自回归(AR)模型阶数, hk包含观测值[y(k-1), …, y(k-p)], ak表示k时刻的TVAR系数向量, e(k)为方差为R的激励高斯白噪声。若TVAR系数ak随时间线性变化, 即
式中,A为状态转移矩阵, wk是方差为Q的高斯噪声。由于(1)式、(2)式分别和状态空间模型中的测量方程、状态方程一致[5], 本文采用卡尔曼滤波及其改进算法实现对TVAR模型系数的估计。
1.2 卡尔曼滤波平滑
工程实际中, 为了得到更准确的参数估计值, 在传统卡尔曼滤波基础上发展了3种高斯最优平滑[6]:
1) 固定点平滑:令yk=[y1, y2, …, yk]为k时刻内所有观测值组成的向量, 通过yk估计0到k-1时刻中某个时刻j(k=j+1, j+2, …)的状态xj的平滑称作固定点平滑。其平滑公式如下
式中, N(xk-n|mk-n|k, Pk-n|k)表示多元高斯概率密度, 均值为mk-n|k, 协方差为Pk-n|k, k值逐渐增大, j为固定值。在实际应用中, 如果需要特别对实验中某一重要时刻状态进行估计时通常采用固定点平滑方法。
2) 固定滞后平滑:利用yk来估计k-N时刻的状态xk-N, N为某个确定的固定滞后值, 该平滑称作固定滞后平滑。其平滑公式为
固定滞后平滑在通讯和遥测数据的处理中具有广泛应用, 适用于对信号估计精度有一定要求的工程项目中。
3) 固定区间平滑:利用固定时间区间(0, M]中得到的所有测量值yM=[y1, y2, …, yM]来估计区间中每个时刻的状态xk(k=1, 2, …, M), 该平滑称作固定区间平滑。平滑公式表示为
固定区间平滑通过使用时间区间的所有观测值yN=[y1, y2, …, yN]对区间每一时刻的状态进行最优估计, 而滤波过程只是由t1及tk时刻之间的观测值yk=[y1, y2, …, yk]作最优估计, 在此情况下, 区间平滑过程通过使用比滤波过程更多的观测值来改善状态估计的精度, 这一平滑方法相对于固定点平滑和固定滞后平滑更能适应颤振数据处理对于估计精度的要求, 基于该方法, 建立如下卡尔曼滤波平滑方程
式中, at|N=E{at|Y1:N}, Pt|N=E{(at-at|N)(at-at|N)T}, 定义Jt-1=Pt-1|t-1ATPt|t-1, 这样就在原卡尔曼滤波方程的基础上加入平滑过程, 并为后续EM-KS算法的引入奠定基础。
1.3 EM-KS算法
在卡尔曼滤波实际应用中, 由于状态方程和观测方程的噪声方差矩阵Q, R以及状态转移矩阵A未知, 传统的方法是根据经验直接使用不准确的设定值作为算法的参数, 这种处理不仅会导致估计参数误差增大, 还会引起后续提到的滤波发散问题[7]。基于此, 本文将EM算法引入卡尔曼滤波过程中, 在卡尔曼滤波平滑方程的基础上借助EM算法的极大似然概念, 从已得到的测量值出现概率最大的角度对颤振信号的{A, Q, R}参数进行实时估计, 以保证滤波器能更好适应噪声统计特性的变化, 借此得到更准确的参数估计值, 并在一定程度上提高算法的收敛性[8]。
期望最大化算法通常包括2个步骤:①计算期望(E步骤), 即基于系统状态初始值{X0, P0}以及{A, Q, R}的现有估计值, 计算其极大似然值; ②第二步是最大化(M步骤), 即最大化在第一步求得的极大似然值, 得到最优估计参数。同时, M步骤得到的估计参数将被用于下一个E步骤中, 实现迭代运算, 直到似然值收敛。为了实现对相关参数矩阵的最优估计, 本文中的EM算法是在卡尔曼滤波平滑运算的基础上得到的, 具体推导过程如下:
1) E步骤
假设实际噪声符合高斯分布, 以其概率密度函数的对数形式建立似然函数
对似然函数求取期望
为便于M步骤的进一步计算, 令
2) M步骤
最大化是针对参数θ={A, Q, R, X0, P0}, 即实现θML=maxθlnp(Y1:N|θ), 根据梯度下降算法, 当系统参数满足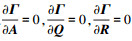 时, 该参数即是使对数似然值期望最大的估计值, 得到的更新方程如下
时, 该参数即是使对数似然值期望最大的估计值, 得到的更新方程如下
且初值X0=a1|N, P0=P1|N。
1.4 卡尔曼滤波的发散问题
卡尔曼算法在实际应用中, 由于新息的不断加入, 估计误差随迭代过程的进行也不断增大, 导致了滤波的发散现象[9]。究其原因, 首先, 所建模型与实际系统存在偏差, 使得模型与获得的测量值不匹配而导致滤波发散。再者, 卡尔曼滤波算法是递推实现的, 受限于计算机字节的长度, 随着滤波步数的增加, 舍入误差的积累会使估计方差阵失去非负定性和对称性, 进而导致计算发散。
衰减记忆滤波和限定记忆滤波等方法在一定程度上能抑制滤波发散问题, 但与此同时也牺牲了滤波器的最优性而成为次优滤波方法。由于EM-KS算法能够得到更为精确的噪声协方差矩阵, 并且随着观测值的加入不断迭代更新, 保证了卡尔曼算法的收敛性。针对计算发散问题, Potter提出了平方根滤波的概念, 即在卡尔曼滤波方程中不传递易失去正定性的协方差矩阵, 取而代之的是传递其平方根, 这样这个分解因子的平方在任何时候都能保证正定性[10]。算法流程如表 1所示。
通过将平方根滤波算法加入EM-KS算法中, 这样在获得较好的滤波收敛性的同时, 也避免了因计算机累积的舍入误差的影响而导致的计算发散问题, 保障了滤波的精度和稳定性。
平方根滤波算法
2 颤振时域判据
传统的颤振边界预测(FBP)方法以阻尼外推法为代表, 由于模态阻尼受噪声影响较大, 使其在连续变速试验中无法得到准确的估计值。由Zimmerman和Werssenburger提出的基于连续系统的Routh颤振裕度判据在一定程度弥补了阻尼外推法对阻尼估计精度要求严格的缺陷, 但这种方法不便在计算机上实现, 为此, Matsuzaki提出了离散系统下基于Jury判据的时域稳定性判据[11]。
通过采用ARMA模型来描述大气紊流激励的物理系统, 其中AR模型包含系统的响应项, MA模型代表白噪声激励, 相应的差分方程表示如下
式中, y(n)为响应信号, e(n)为紊流激励。M代表系统的阶次, 通常M的取值应该大于等于试验件模态数。由于模型的AR部分关乎系统的稳定性, 因而仅使用该部分做稳定性分析。
将Z变换应用于(11)式并假设机翼系统有2个主要模态, 即M=4, 可得系统TVAR部分的特征多项式及展开形式
式中,zi和zi*是多项式的共轭复根。用Jury判据对系统的稳定性进行评判, 系统稳定需要满足如下方程
式中
定义二自由度离散时间系统的颤振裕度(FMDS)如下
应用Tustin变换可证明, 只要采样率足够高, FMDS在数学上等价于颤振裕度。同时也可以将该判据推广到适用于有Na个自由度的多模态系统[12]
通过每次递推估计得到的TVAR系数构造(14)式、(15)式矩阵, 并代入(16)式或(17)式即可得到相应时刻下的FMDS, 对连续变速颤振信号进行处理得到随风速单调变化的稳定性判据, 拟合外推至Fz=0即可获得颤振边界。
3 仿真与实测分析
3.1 仿真分析
对于颤振试验, 从颤振模态相互之间耦合的机理上讲, 可以用一个具有双模态自由度的物理运动方程对其过程进行描述, 即可用如下的四阶差分方程来刻画
设其共轭特征根分别为(λ1, λ1*), (λ2, λ2*), 从而方程系数可以由以下特征根计算式得到
当结构模态按一定规则变化时, 应用(19)式可模拟一个二自由度系统速度的分阶梯或连续变化的颤振过程方程。
现模拟一个长度63 s、采样率为64 Hz的双模态仿真信号, 其频率f1由5 Hz线性变化至10 Hz, 频率f2由20 Hz线性变化至15 Hz, 并加入高斯白噪声以模拟实际噪声环境。仿真信号时间历程见图 1。
为了检验EM-KS算法的估计精度, 分别通过带有遗忘因子的递推最小二乘法(下标FFRLS, 遗忘因子取0.99)和卡尔曼滤波平滑算法的估计结果作为对比, 见图 2。
由图 2可知, EM-KS对KS算法的改善效果明显, 这是由于EM算法的加入得到了相对准确的噪声协方差矩阵, 在一定程度上解决了连续变速试验信号的噪声模型估计不准确的问题, 得到了相对于FFRLS算法同样优秀的估计性能。
由于实际估计中得不到准确的阻尼, 用颤振时域判据代替传统的阻尼方法, 并将EM-KS算法与FFRLS、KS算法预测结果对比, 其中, 为避免KS算法与EM-KS算法计算发散, 加入平方根滤波, 得到的判据曲线及外推曲线如图 3所示, 实际颤振发生时刻为第70 s。
正如图 3中所示, 3种算法的颤振裕度都有着很好的单调下降趋势, 卡尔曼滤波平滑算法由于初始参数与实际偏差太大且没有在一开始就进行相关参数的优化, 在起始10 s之后才渐渐收敛, 为了最后能得到预测值, 只对其10 s后的数据进行拟合外推。相比之下, EM-KS算法与FFRLS算法均是使用全局的数据进行拟合预测, 由于判据单调下降的规律性很强, 在相对靠前的时刻也即实际中的低速状态下就能得到相对准确的预测值, 这对于连续变速颤振试验是至关重要的, 保证了足够的安全裕度。且通过拟合结果可以看到, 在该仿真状态下, EM-KS算法的FBP预测精度明显优于FFRLS和KS算法, 且有着很好的初始性能与收敛性能。
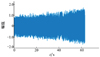 |
图1 仿真信号时间历程 |
 |
图2 仿真信号频率估计对比 |
 |
图3 仿真信号FBP结果对比 |
3.2 实测分析
实测数据取自某型飞机气弹模型尾段低速风洞实验。由于原始信号存在趋势项和低频干扰, 首先对其预处理, 处理后的信号时间历程及相应的速度变化曲线如图 4所示。
使用本文方法进行频率估计和颤振边界预测, 结果如图 5所示。
根据实测数据的处理结果, 可知加入平方根滤波算法的EM-KS方法同样有着很好的频率估计性能与收敛性能。通过对0~40 s时间段内的FMDS值进行二次拟合, 得到Fz=0下的外推值为Vp=40.36 m/s, 这与实际颤振速度Vf=40.68 m/s基本吻合, 故本文方法在实测信号处理过程中也有着很好的预测精度。
 |
图4 实测信号时间历程与速度变化 |
 |
图5 实测信号频率估计与FBP |
4 结论
结合连续变速颤振信号的特点和处理需求, 本文基于EM-KS算法对卡尔曼滤波算法进行改进优化。创新之处在于通过对颤振信号时变状态空间模型参数矩阵的迭代优化来减小其建模误差, 这一步骤既提升了时变系数的估计精度, 在一定程度上也保障了算法的收敛性与稳定性。同时还讨论了卡尔曼滤波的发散问题并提出了采用平方根滤波抑制计算发散的解决方案, 而后给出了时变系统的稳定性判据FMDS并应用于颤振边界预测过程。后经仿真与实测数据验证, EM-KS方法相比自适应和KS算法, 在频率估计与颤振边界预测精度上都有着明显的优势, 对于连续变速颤振试验的安全进行具有重要意义。
References
- Iovnovich M, Nahom T, Presman M, et al. Assessment of Advanced Flutter Flight-Test Techniques and Flutter Boundary Prediction Methods[J]. Journal of Aircraft, 2018(2): 1–13 [Article] [Google Scholar]
- Song Shubiao, Pei Chengming. Recursive Time-Frequency Analysis Method for Signal Processing of Continuous Variable Speed Flutter Test[J]. Journal of Aviation of China, 2005, 18(3): 213–217 [Article] (in Chinese) [Google Scholar]
- Wang Xin. Application of Kalman Filter in Model Parameter Estimation[D]. Harbin, Harbin Institute of Technology, 2008 (in Chinese) [Google Scholar]
- Byrne C L. The EM Algorithm Theory Applications and Related Methods[OB/OL](2017-03-01)[2018-06-08]. https://www.researchgate.net/profile/charles_Byrne2017 [Google Scholar]
- Punales A G S. Time-Varying Coefficient Model and the Kalman Filter: Applications to Hedge Funds[D]. Toronto, Canada, Ryerson University, 2011 [Google Scholar]
- Einicke G A. Smoothing, Filtering and Prediction: Estimating the Past, Present and Future. Rijeka, Croatia: Intech[R]. ISBN 978-953-307-752-9, 2012 [Google Scholar]
- Yu Aihua. Parameter Estimation of Gaussian Mixture Model Based on EM Algorithm[J]. Modern Computer, 2011(17): 3–7 [Article] (in Chinese) [Google Scholar]
- Wang Ge, Yu Hongyi, Shen Zhixiang, et al. A Fast Convergence Parameter Estimation Method Based on EM Algorithm[J]. Journal of Jilin University, 2013, 43(2): 532–537 [Article] (in Chinese) [Google Scholar]
- Zhou Zhenwei, Fang Haitao. Kalman Filter Stability with Random Coefficient Matrix under Inaccurate Variance[J]. Journal of Automation, 2013, 39(1): 43–52 [Article] (in Chinese) [Google Scholar]
- Dong Chunmin, Zhou Wei, Cao Zhentan, et al. Analysis on the Superiority of Square Root Filtering[J]. Surveying and Mapping and Spatial Geographic Information 2012 35(1): 66–68 [Article] (in Chinese) [Google Scholar]
- Matsuzaki Y. An Overview of Flutter Prediction in Tests Based on Stability Criteria in Discrete-Time Domain[J]. International Journal of Aeronautical and Space Sciences, 2011, 12(4): 305–317 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Matsuzaki Y. Flutter Prediction of Multimode Systems from Their Turbulent Responses by Jury's Criterion[C]//54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2013 [Google Scholar]
All Tables
All Figures
 |
图1 仿真信号时间历程 |
| In the text | |
 |
图2 仿真信号频率估计对比 |
| In the text | |
 |
图3 仿真信号FBP结果对比 |
| In the text | |
 |
图4 实测信号时间历程与速度变化 |
| In the text | |
 |
图5 实测信号频率估计与FBP |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


