| Issue |
JNWPU
Volume 37, Number 6, December 2019
|
|
|---|---|---|
| Page(s) | 1102 - 1110 | |
| DOI | https://doi.org/10.1051/jnwpu/20193761102 | |
| Published online | 11 February 2020 | |
Trajectory Estimation of Hypersonic Glide Vehicle Based on Analysis of Aerodynamic Performance
基于气动性能分析的高超声速滑翔飞行器轨迹估计
1
School of Astronautics, Northwestern Ploytechnical University, Xi'an 710072, China
2
Shaanxi Key Laboratory of Aerospace Flight Vehicle Technology, Xi'an 710072, China
Received:
15
November
2018
Due to high speed and high maneuverability of hypersonic glide vehicles (HGVs), the state estimation of such targets has always been a research hotspot. In order to improve accuracy of the trajectory estimation, a nonlinear aerodynamic parameter model for target estimation based on aerodynamic performance analysis is proposed. Firstly, the dynamic characteristics of the hypersonic glide vehicle during the hypersonic gliding stage was analyzed. Then, aiming at HTV-2-liked vehicle, the engineering calculation method was used to form the reference aerodynamic model for the target estimation. Secondly, a deviation model described by first-order Markov process was introduced to compensate the uncertainties of the unknown maneuver information from the target. Finally, extended Kalman filter was utilized to estimate the state of the target. The simulation results show that the proposed model is able to improve the accuracy of acceleration estimation for the HTV-2-liked hypersonic gliding vehicles.
摘要
由于高超声速滑翔飞行器(HGVs)具有高速、高机动的特点,对此类目标的状态估计一直是一个研究热点。鉴于采用传统的运动学和动力学模型进行轨迹估计时加速度估计精度不高,提出一种基于气动性能分析的非线性气动参数目标估计模型。首先,在研究了高超声速滑翔飞行器跳跃再入段运动特性的基础上,以类HTV-2飞行器为研究目标,采用气动力估算方法对高超声速滑翔目标再入段的气动力进行计算分析。其次,建立与马赫数线性相关的气动参数"基准模型"和以一阶马尔可夫过程描述的气动参数"偏差模型",对目标气动参数进行非线性估计。数学仿真结果表明,该方法可以一定程度上提高卡尔曼滤波方法对该类目标的加速度估计精度。
Key words: hypersonic gliding aircraft / maneuvering target estimation / aerodynamic performance / model for aerodynamic parameter
关键字 : 高超声速滑翔飞行器 / 机动目标估计 / 气动性能 / 气动参数模型
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
与传统的弹道导弹武器相比, 高超声速滑翔武器突防能力更强, 飞行空域更大, 同时具有战术和战略价值。美国于2014年提出战术助推-滑翔(TBG)项目, 最高速度为马赫数9, 射程约1 000 km。计划2020年完成武器化实弹试验技术验证测试[1]。另外, 基于TBG项目的技术成果转化和集成, 2018年新启动了空射快速响应武器(ARRW)项目, 着力于先期部件研制和样机开发[2]。在战略助推-滑翔高超声速武器方面, 美国“先进高超声速武器”AHW项目(射程超过6 000 km)发展迅速[3], 2014年后将其由一种陆基发射弹道导弹系统转为海基潜射发射系统, 并于2017年10月30日成功进行了中程高超声速助推-滑翔验证飞行器首次飞行试验[4]。随着高超声速滑翔飞行器技术快速发展, 这类武器已经成为了未来空天防御的战略威胁, 也为反导拦截技术带来了巨大挑战。
轨迹跟踪和估计是防御和拦截HGV武器的基础, 由于HGV在滑翔段加速度可以达到5g~10g, 末段甚至可以达到80g~100g[5], 导致其轨迹复杂多变, 难以进行估计和预测。在进行轨迹跟踪和估计时, 如何构建合理的目标状态估计模型是首要解决的问题。许多学者建立了Singer模型[6]、二阶时间相关模型[7]、匀速转弯模型[8]、半马尔可夫模型[9]和Jerk模型[10]等机动目标模型, 可以统称为目标估计的运动学建模。基于运动学的目标建模优点是实现简单、响应快, 但是这类模型不能准确描述高速高机动目标的运动机理, 也不能表征高超声速滑翔飞行器滑翔段的动力学特征, 因而轨迹跟踪精度差。为了提高估计精度, 后续研究主要集中在对目标的动力学特性进行建模。一类方法是直接对加速度进行估计, 如王国宏和曹亚杰等[11-12]针对特定的周期机动目标, 将加速度建立为正弦波自相关随机过程, 但是对非周期机动目标, 由于模型的不匹配将导致精度下降。文献[13]分析了高超声速滑翔飞行器典型的机动飞行模式, 采用多模型方法匹配目标的机动模式, 这是对估计精度、滤波器稳定性和收敛速度等因素的折中方案。文献[14]采用非线性马尔可夫过程描述目标加速度, 基于目标可能机动的统计构建机动的系统噪声幅值, 令加速度的过程噪声和动压正相关, 有效提高了状态估计精度。但是这种方法依赖目标机动控制量的统计规律等先验信息, 这在实际应用中很难获得。另外一类是将气动系数或控制量作为扩展状态进行估计, 过程噪声被引入在初始状态中, 在状态预测和更新过程中, 噪声的影响就可以在非线性系统中进行传输和估计。特别是当系统噪声和观测噪声影响较大时, 可以使滤波结果更好地接近真实值。文献[15]考虑到飞行器机动主要受升力的影响, 在弹道坐标系(VTC)内描述升力的作用, 用一阶马尔可夫过程建立气动力参数模型。文献[16]认为高超声速滑翔飞行器纵向机动能力有限, 进行轨迹估计的重点应放在目标横向机动的估计上。作者在文献[17]的基础上, 采用随机过程建模, 将气动参数和滚转角进行扩维估计。文献[18]采用容积卡尔曼滤波方法对机动目标状态估计, 将攻角和倾侧角2个控制变量建立为高斯模型。这些研究将与目标加速度相关的估计量按高斯模型或一阶马尔科夫模型描述, 虽然可以在一定程度提高估计器的适应性, 但当所建模型与实际模型不匹配时, 估计精度会大幅降低甚至造成滤波器发散。
由于高超声速滑翔目标在再入过程中, 气动力是目标实现大范围机动的主要因素, 如何减小气动力估计误差是提高高超声速滑翔飞行器轨迹估计精度的关键。
本文首先在高超声速滑翔飞行器运动特点的基础上以类HTV-2飞行器为研究对象, 研究目标的气动性能, 挖掘目标状态估计所需先验信息。其次, 对目标动力学模型进行分析, 并将带有误差的气动数据作为先验信息引入状态方程, 建立以一阶马尔可夫过程描述的气动参数偏差模型, 对目标气动参数进行估计。由于高阶滤波会使计算量成倍提高, 因此提出基于气动参数偏差模型的扩展卡尔曼滤波(extended Kalman filter, EKF)方法进行仿真验证。
1 高超声速滑翔目标气动性能分析
目标所受的气动力直接影响飞行器的运动状态, 如果将目标的气动特性作为先验信息的重要组成部分, 其中包含信息量的多少会直接影响目标状态估计模型的准确度。由此, 虽然无法获得真实的目标三维模型, 但是为了对目标气动特性进行定量分析, 采用二次曲线法[19]对类HTV-2高超声速滑翔目标进行参数化建模, 并对参数化三维模型进行气动计算, 进而得到不同飞行条件下的气动性能, 为目标状态估计研究提供先验知识。飞行器的参数化建模三维效果如图 1所示。
为提高计算效率和可靠性, 采用气动力工程计算方法[20]对类HTV-2高超声速滑翔飞行器参数化模型进行气动特性分析。图 2给出目标在40 km高度飞行时, 不同马赫数下升阻比随攻角的变化趋势曲线。发现目标的最大升阻比与飞行马赫数正相关, 且出现在10°攻角左右; 最大升阻比在马赫数2~18时约为4, 这符合文献[21]的论述结果。
目标在高度为40 km飞行时的气动系数随马赫数的变化如图 3和图 4所示。从计算结果可以看出:高超声速(Ma>5)情况下:①目标在定攻角条件下飞行时, 升力系数和阻力系数均随马赫数近似线性变化; ②不同攻角下, 升力系数和阻力系数关于马赫数的线性函数的斜率和截距接近。
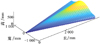 |
图1 目标气动外形的参数化三维模型 |
 |
图2 升阻比随攻角变化曲线 |
 |
图3 升力系数随马赫数变化曲线 |
 |
图4 阻力系数随马赫数变化曲线 |
2 高超声速滑翔再入目标的数学描述
2.1 目标的运动模型
假设地球为均匀圆球体, 考虑地球自转, 并且目标以零侧滑角飞行, 在半速度坐标系下建立目标再入过程三自由度动力学方程[22]
式中, 状态量r, θ, ϕ, V, γ, ψ分别为目标地心距、经度、纬度、速度、航迹角和航向角。σ为倾侧角, Cγ和Cψ分别为地球自转引起的附加项。无动力高超声速滑翔飞行器再入过程中, 空气动力的作用远大于重力的作用, 而哥氏力和地球扁率的作用更小, 可以忽略, 所以假定其机动再入运动为无机动运动和升阻力作用效果的累加[23]。L和D分别为升力加速度和阻力加速度, 可以写为
式中,q=ρv2/2为动压, S为飞行器参考面积, m为飞行器质量。CL和CD分别为飞行器的升力系数和阻力系数。
2.2 雷达站坐标系下的动力学模型
定义雷达站坐标系为东北天坐标系(ENU), 则高超声速滑翔飞行器在雷达参考坐标系下运动的非线性微分方程可以描述为[14]
公式中, r和v分别表示目标飞行器的地心距矢量和速度矢量; a表示目标受气动力产生的加速度; ωe为地球自转角速度; -ωe×(ωe×r)表示离心加速度; 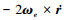 表示科氏加速度; 不考虑地球扁率影响, 重力加速度g表示为
表示科氏加速度; 不考虑地球扁率影响, 重力加速度g表示为
式中,μ为地球引力参数, r表示地心距大小。
文献[16]推导证明了利用气动加速度对目标状态进行扩维可以提供更多先验信息, 以达到减小估计误差的目的。建立目标在ENU坐标系(坐标原点与雷达站位置重合)下的质心加速度方程
式中,r为目标瞬时地心距, x, y, z分别为目标在ENU坐标轴上的分量, B为雷达站地理纬度, Re为地球半径, Ax, Ay, Az分别为气动力在3个方向产生的加速度。
在弹道坐标系下将目标的气动力分解为阻力、转弯力和爬升力。阻力与速度方向相反, 转弯力在当地水平面内与速度方向垂直, 爬升力垂直于阻力和转弯力。据此定义弹道坐标系沿3个轴方向的气动力参数为
由公式(6)可知, αd影响目标的再入速度, αt描述目标的转弯运动, αc描述目标的爬升或俯冲运动。即, 高超声速滑翔目标的机动运动可以由αd以及与αd相互独立的2个参数αt和αc描述。
由公式(5)可以看出气动加速度很大程度上影响目标的运动状态。由坐标转换关系可知, 在ENU坐标系下的气动加速度与气动参数间关系可以表示为[17]
式中, TVTCENU(v)为气动力参数从弹道坐标系到ENU坐标系的坐标转换矩阵
式中,  。
。
3 气动参数建模
本文建立气动参数估计模型的思路是:首先认为目标飞行器按照“基准参数”飞行, 将“基准参数”的待估偏差视为“目标机动”。即将目标运动分解为“基准运动”和“机动运动”来分别进行研究, 再将这两部分运动合成即可得到目标的真实运动状态。
在高超声速滑翔目标状态估计模型中, 升力系数CL和CD不能被认为是常数。因此, 不能简单地将气动参数建立为高斯模型, 同时还需要在一定程度上能表征目标的机动特征。目标气动系数的时变特性导致了气动参数随时间变化, 而高超声速滑翔目标的气动系数是攻角(由目标自动驾驶仪解算得到)和马赫数的函数:CD(α, Ma), CL(α, Ma)。但是飞行过程中攻角的剧烈变化会导致飞行器气动力、热变化复杂, 需要尽可能使气动系数随攻角变化平缓[24-25], 因此可以分别考虑攻角和马赫数对目标状态的影响。根据第2节对类HTV-2飞行器的气动特性分析, 在高超声速(Ma>5)时, 将气动系数分离为受马赫数和攻角分别影响的两部分。其中前者在不同攻角的基础上, 可以简化为马赫数的线性函数, 得到近似的统计规律, 作为目标的“基准运动”
式中, CD0, CD1, CL0, CL1分别为拟合参数。由公式(9)可以建立基准气动参数模型为
式中, αd0, αt0和αc0分别为描述“基准运动”的三轴方向气动参数。
需要特别说明的是, 建立CD(Ma)和CL(Ma)模型的目的是为了尽可能挖掘目标机动特性的先验信息, 用来表征“基准运动”特性。当然, 在实际轨迹估计过程中, 由于拟合参数不够准确或者受到当时气象条件的影响以及制导律决定的攻角和倾侧角变化(统称为“机动因素”), 必然导致建立的“基准参数”与目标的实际飞行参数存在偏差。而目标实际运动为“基准运动”和“机动运动”的合成, 因此实际的目标气动参数可以满足公式(11)关系
式中, αd, true, αt, true和αc, true分别为目标实际飞行的气动参数, αd, error, αt, error和αc, error分别为三轴方向气动参数的偏差量, 用来描述目标的机动过程。假设目标由“机动因素”造成的气动参数偏差为一阶时间相关过程, 则时间相关函数的指数形式为[26]
式中, σα2和λ为决定目标“机动运动”的待定参数, σα2为气动参数偏差量的方差, λ为机动频率。根据经验, 目标转弯机动λ≈1/60, 目标逃避机动λ≈1/20, 大气湍流扰动λ≈1。假设目标气动参数的偏差量均匀分布, 则σα2的概率密度模型为
式中, αmax2为气动参数偏差量的最大值, 此时的概率为Pmax, 目标不机动的概率为P0。对时间相关函数r(τ)应用维纳-科尔莫格罗夫白化方法, 目标的气动参数偏差量可以采用一阶马尔可夫过程及噪声补偿来描述
将目标的机动估计转化为对气动参数的偏差进行估计, 式中λd, λt, λc分别为气动参数偏差量αd, error, αt, error和αc, error对应的机动频率, wd, wt, wc分别为气动参数偏差量αd, error, αt, error和αc, error的零均值高斯白噪声。
4 基于气动参数偏差模型的EKF滤波
采用多模型方法或高阶非线性滤波虽然可以提高目标状态的估计精度, 但不可避免的提高了计算的复杂度。考虑到高超声速滑翔飞行器再入轨迹一般不会出现类似阶跃的状态突变, 为了尽快而且比较准确地估计出气动参数, 本文采用单一模型描述目标的运动形式, 选择工程上应用最广泛的EKF滤波方法进行目标轨迹估计。
根据前文推导, 将气动参数的偏差量扩维至目标的运动状态向量中, 可以得到基于非线性气动参数模型的高超声速滑翔飞行器状态向量
则高超声速滑翔飞行器在雷达站ENU坐标系下的状态方程可写为
式中, w为过程噪声, 可以假设为零均值的高斯白噪声。联立公式(5)、公式(7)、公式(11)、公式(14)和公式(15)可以将非线性方程f(X)表示为
式中, Ax, Ay和Az由公式(7)计算。对公式(16)离散化可以得到
式中, Δt为采样时间间隔, 取决于雷达的跟踪数据率。F(Xk)是f(Xk, tk)相对于Xk的雅可比矩阵。
采用混合坐标系对目标状态进行估计, 即目标状态向量在ENU坐标系下描述, 量测方程建立在雷达坐标系下, 量测值为
式中, R为雷达与目标的径向距离, A为方位角, E为俯仰角。则目标的量测非线性方程为
式中, nR, nA和nE为雷达量测噪声, 假设它们相互独立并服从均值为零的高斯分布。
5 数值仿真实验
本文以高超声速滑翔飞行器(参考美国CAV-H)的再入段为研究对象, 飞行器采用跳跃增程模式飞行, 目标质量970 kg, 参考面积1.02 m2。为了模拟更加真实的攻防对抗仿真环境, 从进攻方的角度在弹道坐标系下设计跳跃滑翔目标再入轨迹(再入点高度90 km, 再入点速度6 500 m/s), 再通过坐标转换得到球坐标系下的数据, 最后加上量测噪声得到实验需要的量测数据。
假设雷达方位角的取值范围:A∈[-180°, 180°), 俯仰角的取值范围:E∈[0°, 20°)。雷达与目标初始距离为925 km, 数据采样率为1 Hz, 径向距离量测标准差为100 m, 方位角、俯仰角量测标准差为2×10-4 rad。由于高超声速滑翔飞行器一般航程较远, 考虑到地球曲率的影响, 假定将地基防御雷达的位置设在东经165°, 北纬12°, 则雷达可观测时间域约300 s。对应的雷达实际观测到的目标轨迹如图 5所示。
为检验本文所建立的估计模型的有效性, 分别采用3种不同的目标状态估计模型对跳跃再入轨迹进行估计, 如表 1所示。完成100次Monte Carlo仿真, 间隔15 s提取一次仿真结果。通过仿真发现模型1、模型2和模型3所需要的计算量相当。
图 6和图 7分别给出了目标的位置估计均方根误差和速度估计均方根误差。从图 6可以看出, 由于量测信息的修正, 所述3种模型中除了模型1的估计误差稍大之外, 3种模型的位置滤波精度相近。在滤波器稳定跟踪阶段, 模型1的位置估计均方差收敛到约70 m量级, 模型2和模型3的位置估计均方差都可以收敛到约50 m的量级; 采用3种模型的全程轨迹跟踪位置均方差都在100 m以内, 这和量测数据的误差量级对应。
由图 7的结果发现, 采用3种模型对目标的速度估计误差均可以较快收敛。在800~900 s内, 由于目标发生大幅度机动, 3种模型均出现局部大幅度跳跃。在对目标稳定跟踪时, 速度估计误差保持平稳趋势, 状态的估计精度依次提高, 但对目标突变机动的敏感程度也依次提高。
由于对非合作目标轨迹估计是为了对目标进行轨迹预报, 因此更加关注目标的加速度信息。图 8~10给出了可以表征目标气动加速度特征的3个方向气动参数滤波均值。
由图 8~10可以看出, 目标气动参数调整幅度较小, 3种模型大致可以反映气动参数的变化, 并在较小的绝对误差带内波动。具体来讲可以得到以下5点结论:①对于气动力的不准确建模会降低目标的气动参数估计精度。②模型1将目标的气动参数认为常值或是缓慢变化的量, 这明显不符合实际。③采用模型1和模型2的气动参数估计结果在目标飞行820 s后才有逐渐收敛的趋势, 这是因为此时目标飞行高度降低, 动压增大, 气动力对目标机动的影响作用逐渐明显, 估计算法对气动参数偏差的修正能力逐渐增强。④模型1和模型2假设目标气动参数为平稳随机过程, 仅通过噪声在非线性系统中传输估计状态量, 误差较大且存在时间延迟。⑤本文提出的模型3引入基准模型作为先验信息的一部分, 不仅考虑了目标气动参数的时变特性, 而且考虑了气动参数的非线性特征, 在估计目标的气动力变化趋势方面最稳定, 估计精度最高, 同时对估计的时间延迟有一定的抑制。这在后续对目标轨迹预报的研究中将起重要作用。
为定量比较3种模型的估计性能, 位置、速度和气动参数误差统计平均值如表 2所示。可以看出, 虽然3种模型的位置估计性能接近, 但是采用模型3的气动参数估计性能明显优于模型1和模型2。
综上所述, 基于非线性气动参数模型的高超声速再入轨迹估计算法可以有效降低机动目标状态估计的均方根误差, 其状态估计和机动辨识性能显著优于其他基于气动力参数的估计算法。
 |
图5 雷达实际观测到的目标轨迹 |
状态估计模型
 |
图6 目标的位置估计均方根误差 |
 |
图7 目标的速度估计均方根误差 |
 |
图8 阻力气动参数滤波均值 |
 |
图9 转弯力气动参数滤波均值 |
 |
图10 爬升力气动参数滤波均值 |
位置、速度和气动参数误差统计平均值
6 结论
本文针对高超声速跳跃滑翔再入飞行器的状态估计问题, 以类HTV-2飞行器为例, 采用工程估算方法对目标在再入滑翔段的气动力特性进行了仿真实验, 充分挖掘了目标的先验信息, 提出了一种基于气动性能分析的状态估计算法。首先通过对气动参数的“基准量”先验信息分析和对气动参数“偏差量”建模, 然后对传统的基于气动力参数的状态估计模型进行改进, 最后利用EKF构建基于气动参数偏差模型的目标状态估计算法。
仿真结果表明, 本文提出的估计模型在不增加计算量的前提下在目标速度状态估计的精度上具有更高的估计精度, 对于大机动的跳跃滑翔目标状态估计具有较强的适应性和鲁棒性。另外, 基于气动参数的非线性趋势分析可以为进一步的目标轨迹预报提供合理的先验信息, 提高拦截概率。
References
- Guan Chengqi, Ning Guodong, Wang Yipeng, et al. Review of Hypersonic Weapon Development Abroad in 2016[J]. Aerodynamic Missile Journal, 2017(3):3–6 [Article] (in Chinese) [Google Scholar]
- Lin Xubin, Li Yan, Hu Dongdong. Analysis on the Budget of Hypersonic Scientific Research of the US Military in 2019[J]. Aerodynamic Missile Journal, 2018(6):1–3 [Article] (in Chinese) [Google Scholar]
- Hu Dongdong, Liu Xiaoming, Zhang Shaofang, et al. Review of Hypersonic Technologies Progresses Abroad in 2016[J]. Tactical Missile Technology, 2017(1): 28–33 [Article] (in Chinese) [Google Scholar]
- Wang Lu, Han Hongtao, Wang Youli. Review of Foreign Hypersonic Technology in 2017[J]. Space International, 2018(3):43–47 [Article] (in Chinese) [Google Scholar]
- Hough M E. Acceleration Characterization for Reentry Orbit Determination with Unmodeled Maneuvers[J]. Journal of Guidance Control & Dynamics, 2018(5):1–13 [Article] [Google Scholar]
- Wei Xiqing, Gu Longfei, Li Ruikang, et al. Trajectory Tracking and Prediction of HypersonicVehicle Based on Singer Model[J]. Aerospace Control, 2017(4): 62–72 [Article] (in Chinese) [Google Scholar]
- Ozkaya B, Arcasoy C C. Analytical Solution of Discrete Colored Noise ECA Tracking Filter[J]. IEEE Trans on Aerospace and Electronic Systems, 1998, 34(1): 93–102 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Klein I, Bar-Shalom Y, Rusnak I. Observability Analysis for Tracking of Coordinated Turn Maneuvers[C]//Proceedings of the 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel, 2014 [Article] [Google Scholar]
- Moose R. An Adaptive Estimator with Learning for a Plant Containing Semi-Markov Switching Parameters[J]. IEEE Trans on Systems, Man, and Cybernetics, 1973(3): 277–281 [Article] [Google Scholar]
- Mahapatra P R, Mehrotra K. Mixed Coordinate Tracking of Generalized Maneuvering Targets Using Acceleration and Jerk Models[J]. IEEE Trans on Aerospace and Electronic Systems, 2000, 36(3): 992–1000 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Wang Guohong, Li Junjie, Zhang Xiangyu, et al. A Tracking Model for the Near Space Hypersonic Slippage Leap Maneuvering Target[J]. Acta Aeronautica et Astronautica Sinica, 2015(7): 2400–2410 [Article] (in Chinese) [Google Scholar]
- Cao Yajie, Li Junlong, Qin Lei. Study on Tracking Filter Algorithms for Nonballistic Targets in Near Space[J]. Journal of System Simulation, 2016(6): 1351–1358 [Article] (in Chinese) [Google Scholar]
- Qin Lei, Zhou Di, Li Junlong. Tracking Filter for Nonnallistic Near Space Targets Based on NVSIMM Algorithm[J]. Systems Engineering and Electronics, 2017, 39(7): 1582–1589 [Article] (in Chinese) [Google Scholar]
- Hough M E. Reentry Maneuver Estimation Using Nonlinear Markov Acceleration Models[J]. Journal of Guidance Control and Dynamics, 2017, 40(7): 1693–1710 [Article] [CrossRef] [Google Scholar]
- Wu Nan, Chen Lei. Adaptive Kalman Filtering for Trajectory Estimation of Hypersonic Glide Reentry Vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2013(8): 1960–1971 [Article] (in Chinese) [Google Scholar]
- Zhang Kai, Xiong Jiajun, Han Chunyao, et al. A Tracking Algorithm of Hypersonic Glide Reentry Vehicle via Aerodynamic Model[J]. Journal of Astronautics, 2017(2): 123–130 [Article] (in Chinese) [Google Scholar]
- Li X R, Jilkov V P. Survey of Maneuvering Target Tracking. PartⅡ:Motion Models of Ballistic and Space Targets[J]. IEEE Trans on Aerospace and Electronic Systems, 2010, 46(1): 96–119 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Fan Y, Zhu W, Bai G. A Cost-Effective Tracking Algorithm for Hypersonic Glide Vehicle Maneuver Based on Modified Aerodynamic Model[J]. Applied Sciences, 2016, 6(10): 312 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Xia Chenchao, Zhao Wenwen, Chen Weifang, et al. Research on Parameterized Modeling and Automatic Mesh Generation of HTV-2-Like Lifting Body[C]//Chinese National Symposium on Shock Waves, 2012 (in Chinese) [Google Scholar]
- Cheng Feng, Tang Shuo, Zhang Dong. Design and Applications of Preliminary Evaluation Platform of Aerodynamic Forces for Supersonic/Hypersonic Vehicles[J]. Journal of Northwestern Polytechnical University, 2018, 36(6): 1076–1084 [Article] [Article] (in Chinese) [CrossRef] [Google Scholar]
- Walker S, Sherk J, Shell D, et al. The DARPA/AF Falcon Program: The Hypersonic Technology Vehicle #2(HTV-2) Flight Demonstration Phase[C]//AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2008 [Article] [Google Scholar]
- Vinh N X. Optimal Trajectories in Atmospheric Flight a2-Napolitano, l.G[M]. Oxford, Pergamon Press, 1982: 449–468 [Google Scholar]
- Zhao Hanyuan. Reentry Dynamics and Guidance of Aircraft[M]. Changsha, University of National Defense Science and Technology Press, 1997 (in Chinese) [Google Scholar]
- Zhu Huiyu, Wang Gang, Sun Quanhua, et al. Numerical Evaluation on Areodynamics of Typical Hypersonic Configurations for Hypersonic Flight[J]. Acta Aerodynamica Sinica, 2012, 30(3): 365–372 [Article] (in Chinese) [Google Scholar]
- Zhan Peiguo. Aerodynamic Analysis of US Army Advanced Hypersonic Weapon[J]. Aeronautical Science & Technology, 2015(1): 7–11 [Article] (in Chinese) [Google Scholar]
- Singer R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J]. IEEE Trans on Aerospace and Electronic Systems, 1970, 6(4): 473–483 [Article] [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 目标气动外形的参数化三维模型 |
| In the text | |
 |
图2 升阻比随攻角变化曲线 |
| In the text | |
 |
图3 升力系数随马赫数变化曲线 |
| In the text | |
 |
图4 阻力系数随马赫数变化曲线 |
| In the text | |
 |
图5 雷达实际观测到的目标轨迹 |
| In the text | |
 |
图6 目标的位置估计均方根误差 |
| In the text | |
 |
图7 目标的速度估计均方根误差 |
| In the text | |
 |
图8 阻力气动参数滤波均值 |
| In the text | |
 |
图9 转弯力气动参数滤波均值 |
| In the text | |
 |
图10 爬升力气动参数滤波均值 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


