| Issue |
JNWPU
Volume 38, Number 3, June 2020
|
|
|---|---|---|
| Page(s) | 523 - 532 | |
| DOI | https://doi.org/10.1051/jnwpu/20203830523 | |
| Published online | 06 August 2020 | |
Algorithm of Reentry Guidance for Hypersonic Vehicle Based on Lateral Maneuverability Prediction
基于侧向机动能力预测的高超声速飞行器再入制导算法研究
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
Xi'an Institute of Space Radio Technology, Xi'an 710100, China
Received:
5
July
2019
Aiming at the problem that the traditional error corridor guidance method has poor adaptability in lateral guidance of predictor-corrector guidance, an algorithm of reentry guidance based on the vehicle lateral maneuverability prediction is proposed without increasing the calculation too much. The lateral component mean value of lift at reentry is calculated by using the bank angle magnitude function obtained from longitudinal guidance. According to the above-mentioned, a crossrange corridor with dynamic boundary constraint is designed to control bank angle reversal timing. Online parameters estimation is introduced to suppress the influence of the atmospheric density and aerodynamic parameters disturbance on the predictor model. The CAV-L, a kind of hypersonic vehicle, is used as an object to carry out reentry guidance simulation. The results show that the guidance algorithm can effectively guide vehicle to target for reentry missions of different range, the landing point error are small and the guidance effect is stable. The simulated results via Monte Carlo method verify that the guidance algorithm has a good adaptability and robustness to initial state deviations and process disturbances.
摘要
针对预测-校正制导中侧向制导使用传统误差走廊制导法自适应能力差的问题,在不过多增加计算量的前提下,提出一种基于飞行器侧向机动能力预测的再入制导算法。利用纵向制导所得倾侧角幅值函数计算飞行器再入时升力侧向分量均值,依此设计边界约束动态变化的横程走廊控制倾侧角反转时机。引入在线参数估计以抑制再入过程中大气密度和飞行器气动参数扰动对预测模型的影响。以CAV-L高超声速飞行器为对象,进行再入制导仿真。结果表明对不同航程的再入任务该制导算法均能有效引导飞行器飞向目标,落点误差小,制导效果稳定。Monte Carlo仿真验证了制导算法对再入初始状态偏差和过程扰动具有良好的自适应性和鲁棒性。
Key words: reentry guidance / hypersonic vehicle / predictor-corrector guidance / lateral guidance
关键字 : 再入制导 / 高超声速飞行器 / 预测-校正制导 / 侧向制导
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
再入制导的目的是在满足过程约束的前提下, 将飞行器准确地从再入点引导至目标点。根据制导指令产生方式的不同, 再入制导法可分为标准轨道制导法和预测-校正制导法两类。标准轨迹制导法已在航天飞机上成功应用, 其特点是对制导系统的在线计算能力要求不高, 再入走廊约束在轨道设计之初便可充分考虑, 但当实际轨迹偏离标准轨道过大时, 制导性能会显著下降, 且对不同的再入飞行任务需要设计不同的标准轨道[1-2]。在线轨迹优化是标准轨迹制导法一个发展方向, 随着优化算法的改进和弹上计算能力的提高, 凸优化等方法被用于标准轨迹快速生成[3]。预测-校正制导法不依赖标准轨道, 而是以期望的终端状态为目标, 再入时不断根据当前飞行状态预测终端状态, 根据预测值与期望值的偏差生成制导指令[4-5]。该制导法对再入任务不确定、再入初始条件变化和再入过程扰动的影响具有很强的鲁棒性, 具有比标准轨道制导法更高的制导精度。
不论是标准轨道制导法还是预测-校正制导法, 都是将纵向与侧向制导分开处理, 用倾侧角幅值控制纵向制导, 倾侧角符号控制侧向制导。对于纵向制导, 标准轨道制导法根据再入任务事先设计好纵向参考轨迹剖面, 实际再入过程中利用当前状态与参考值的偏差计算倾侧角幅值修正量, 而预测-校正制导法则根据再入运动方程实时预测终端状态, 采用迭代算法搜索满足纵向制导要求的倾侧角幅值控制量, 这是2种再入制导法的本质区别。对于侧向制导, 2种方法一般都采取走廊约束方式, 用航向角误差走廊或横程走廊调整倾侧角符号, 将飞行器引向目标。文献[6-10]选取航向角偏差作为走廊约束量, 当航向角偏差大于边界值时倾侧角反转。这种方法的缺点是随着再入飞行器逐渐接近目标点, 航向角偏差波动会越来越大, 致使再入末端发生多次反转。文献[11-13]利用再入横程变化相对缓慢的特点设计了漏斗形的横程走廊, 避免再入末端不必要的倾侧角反转。文献[14]为防止横程参数超出走廊边界, 用横程加横程微分项作为反转控制量。文献[15]同时考虑航向角偏差和横程影响, 将两者加权得到归一化误差, 用于侧向走廊约束量。上述方法均需要根据再入情况的变化, 再入任务纵、横程的大小人为调整侧向误差走廊边界, 且此类方法对再入过程中的升阻比扰动和环境变化影响适应能力差。文献[16-20]在纵向制导得到倾侧角幅值函数后, 利用侧向预测算法确定反转时机, 并根据实际升阻比进行调整。这类方法制导精度高, 自适应能力强, 但需要在每个制导周期内同时进行纵向制导计算和侧向运动积分预测, 计算量大, 对弹上计算机要求高。
针对上述问题, 本文以预测-校正制导法为基础, 提出一种侧向机动能力预测的再入制导算法。在纵向轨迹预测时对飞行器升力侧向分量进行求均值计算, 依此均值动态调整侧向走廊宽度, 控制倾侧角反转时机, 并对大气密度和飞行器气动参数进行在线估计与修正, 提高预测算法收敛性。
1 再入运动方程
高超声速飞行器一般采用无侧滑角、无动力滑翔的方式再入, 假设再入过程中其质量不变, 考虑地球引力J2项摄动, 在地心固联坐标系下建立无量纲的三自由度再入运动方程[21]
式中: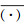 表示无量纲量;
表示无量纲量;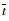 为时间;
为时间;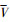 为高超声速飞行器再入速度;γ为航迹角;ψ为航向角;
为高超声速飞行器再入速度;γ为航迹角;ψ为航向角;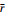 为飞行器质心到地心的距离;θ为经度;ϕ为地心纬度;σ为倾侧角;
为飞行器质心到地心的距离;θ为经度;ϕ为地心纬度;σ为倾侧角;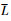 和
和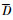 分别为升力和阻力;
分别为升力和阻力; 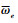 为地球自转角速度;
为地球自转角速度; 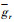 和
和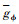 分别为引力加速度径向分量和子午向分量。
分别为引力加速度径向分量和子午向分量。 和
和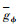 的计算公式如下所示:
的计算公式如下所示:
式中:ρ为大气密度; m为飞行器质量; S为飞行器气动参考面积; Re为地球赤道半径; CL和CD分别是飞行器升力系数和阻力系数, 其值由飞行攻角α和马赫数决定。
再入运动方程组中控制量为攻角α和倾侧角σ。由于攻角是影响再入机动范围、飞行器气动特性和飞行热力学环境的直接因素, 频繁且大幅调整攻角将增加制导系统、姿控系统和热防护系统负担, 因此攻角一般事先设计成关于马赫数的分段线性函数。
式中:α1为最大飞行攻角; α2为最大升阻比对应攻角; Ma1和Ma2根据航程需求确定。将倾侧角作为再入主要控制量。再入过程受热流、动压和过载约束, 再入终端要满足落点位置要求。
2 预测-校正制导
高超声速飞行器再入飞行时, 在一个制导周期内, 对再入纵向轨迹进行预测, 根据航程偏差校正倾侧角幅值, 并利用纵向制导确定的倾侧角幅值函数预测飞行器侧向机动能力, 调整侧向走廊宽度, 控制倾侧角符号。得到倾侧角的幅值和符号后, 就可以根据当前飞行状态和再入运动方程(1)~(6)式, 仿真计算本制导周期内的三自由度再入轨迹。进入下一制导周期, 如此循环, 直到满足再入终端条件, 使飞行器飞向落点位置。预测-校正制导逻辑框图如图 1所示。
 |
图1 预测-校正制导逻辑框图 |
2.1 纵向制导
纵向制导通过纵向再入预测方程计算满足再入纵向终端约束的飞行航程, 与当前实际剩余航程比较后利用牛顿割线法确定符合航程要求的倾侧角幅值指令。
为快速积分预测纵向再入轨迹, 在再入运动方程(1)、(2)、(4)式的基础上, 忽略地球自转影响及引力摄动, 可得仅与参数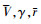 相关的纵向再入预测方程。
相关的纵向再入预测方程。
纵向制导要在线确定倾侧角幅值, 需对其进行参数化处理, 将过程寻优问题转化为单参数搜索问题。令
式中:V1, V2和Vx分别为再入起始点、再入终端和再入过程中某一时刻的速度;σ1, σ2和σx是与之相对应的倾侧角幅值;V1, V2, Vx和σ1, σ2均为确定值。在任意V值下, |σ|随σx单调递增, 参数σx用来确定随速度变化的倾侧角幅值曲线。
给定初始倾侧角幅值函数, 在一个制导周期内, 以当前再入状态为初始量对纵向再入预测方程及(16)式积分, 忽略航向角偏差, 可算出到再入终端的预测航程。
实际剩余航程Stogo为飞行器当前位置(θ, ϕ)到落点位置(θf, ϕf)的大圆弧长。
倾侧角幅值参数σx和预测航程Spre之间为单调非线性关系, 通过牛顿割线法可以快速搜寻到合适的σx值, 使预测航程Spre等于剩余航程Stogo, 迭代计算公式为
由此能确定当前制导周期内的倾侧角幅值曲线, 生成纵向制导指令。
2.2 侧向制导
侧向制导的目的是确定倾侧角反转时机, 使飞行器在侧向平面内飞向落点位置。在满足落点精度要求的前提下, 再入过程倾侧角反转次数不宜过多, 以免加重姿控系统负担, 且倾侧角反转还会引起再入轨迹跳跃。
侧向制导一般通过基于漏斗曲线的开关控制方式调整倾侧角符号。飞行器再入前预先设计好航向角或横程误差走廊边界, 当实际再入过程中航向角或横程偏差超过所设计的边界值时倾侧角符号反转。走廊边界的大小与纵向制导所得的倾侧角幅值函数密切相关, 因为较大的倾侧角幅值会增加升力在侧向的分量, 引起较大的航向角和横程变化, 需要设计一个较大的误差走廊边界以避免倾侧角反转次数过多; 反之, 较小的倾侧角幅值需要设计较小误差走廊边界, 以避免飞行器错过反转时机, 无法到达落点位置。这类方法要求再入过程中倾侧角幅值函数不能有较大的不确定性, 且需要根据落点位置和纵、横程的不同事先调整误差走廊边界。在应对不同再入任务或再入过程不确定性扰动较强的情况下, 这类方法自适应能力差, 制导精度难以保证。
针对上述问题, 可设计走廊边界动态变化的侧向制导策略。在当前制导周期内, 通过纵向制导确定倾侧角幅值函数后, 利用纵向预测轨迹参数可计算飞行器升力侧向分量的均值J, 用以表征飞行器侧向机动能力。
式中: 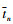 为当前时刻;
为当前时刻; 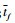 为预测终端时刻。
为预测终端时刻。
再入过程中飞行器到落点的视线角为
航向角偏差Δψ定义为从飞行器指向落点的矢量与速度在当地水平面投影矢量之间的夹角。
横程χ与Stogo, Δψ的关系为
再入过程中, 相对于航向角偏差, 横程变化较为平缓稳定, 故选取横程作为侧向走廊约束量。飞行器侧向机动能力越强, 横程走廊边界可设置地越大, 减少倾侧角反转次数, 同时, 为确保侧向落点精度, 飞行器越接近目标点, 走廊边界应该越小, 即边界值随剩余航程Stogo的减小而减小。因此, 设计如(23)式所示的横程走廊边界, 其值根据再入飞行器侧向机动能力动态调整。
式中, c为横程走廊边界系数。c越小横程走廊约束越严格, 再入过程倾侧角反转次数越多, 侧向制导精度越高, 反之, 约束越宽松, 反转次数越少, 侧向制导精度越低。在不引起纵向再入轨迹频繁跳跃和增加姿控系统负担的前提下, 应尽量选择较小的走廊边界系数。
侧向制导策略可表述为:当横程满足|χ| < Δχ的条件时, 倾侧角符号保持不变, 当横程超出走廊边界值时, 倾侧角符号反转, 并维持当前符号继续飞行, 直到下次横程超出另一侧走廊边界值时再次反号。其表达式描述为
2.3 参数估计
高超声速飞行器再入过程中大气密度、风场等参数的不确定性扰动对气动力影响较大。为提高纵向再入预测的准确性, 需根据实际飞行状态对标准大气模型进行修正。
由惯性测量组合的输出可得再入时升力加速度和阻力加速度的测量值, 分别记为 和
和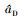 。利用阻力加速度计算公式, 能算出对应阻力加速度
。利用阻力加速度计算公式, 能算出对应阻力加速度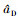 的大气密度估计值
的大气密度估计值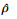
式中,(·)nom表示标称气动参数。
由大气密度估计值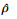 和标称大气密度ρnom可以得到大气密度修正因子Kρ
和标称大气密度ρnom可以得到大气密度修正因子Kρ
纵向再入预测时, 用(26)式计算的大气密度修正因子对标称大气密度进行修正, 修正后的大气密度为
实际应用中, 惯性测量组合输出的阻力加速度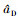 是带有测量噪声的信号, 需采用一阶低通滤波器对大气密度修正因子Kρ进行消噪处理。
是带有测量噪声的信号, 需采用一阶低通滤波器对大气密度修正因子Kρ进行消噪处理。
式中:Kρ(i)表示当前时刻大气密度修正因子, Kρ(i-1)为上一时刻值;kρτ为一阶低通滤波器增益系数。kρτ在0~1之间取值, 其值越趋近于0, 对高频波动的抑制效果越明显, kρτ的计算式为
式中:τρ为滤波器时间常数;Δt是惯性测量组合输出信号的间隔时间。
再入过程中环境因素和飞行器自身不确定性偏差对实际升阻比有很大影响。因此, 升阻比在线修正也是提高纵向预测精度的重要环节。与大气密度修正方法相同, 设升阻比修正因子KL/D为
式中: 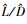 是升阻比估计值, 其计算式为(31)式; (L/D)nom是标称升阻比, 其计算式见(32)式。
是升阻比估计值, 其计算式为(31)式; (L/D)nom是标称升阻比, 其计算式见(32)式。
同样, 对升阻比修正因子KL/D进行一阶低通滤波消噪处理。
根据修正的大气密度和升阻比可得纵向再入预测时的升力和阻力修正值分别为
3 仿真验证
仿真计算以高超声速再入飞行器CAV-L为对象, 质量m=816.48kg, 气动参考面积S=0.322 58 m2, 升、阻力系数参见文献[21]。攻角曲线参数为:α1=20°, α2=10°, Ma1=18, Ma2=16, 再入过程中攻角速度不超过2°/s。倾侧角幅值曲线参数为:V1=7 000 m/s, Vx=5 600 m/s, V2=0 m/s, σ1=56°, σ2=69°, 倾侧角幅值限制在5°~80°之间, 角速度不超过5°/s。横程走廊边界系数c取0.45。一阶低通滤波器时间常数τρ=1, τL/D=1。目标点经纬坐标为(242°, 34°), 海拔高度300 m。USSA-1976标准大气模型用于三自由度再入轨迹仿真, 简化的指数大气模型用于纵向再入预测。制导周期采用变步长形式, 再入初期预测-校正制导间隔为100 s, 随着飞行器接近目标点, 逐渐提高至5 s。再入制导仿真以飞行器当前高度接近目标高度(高度差小于1 km)时剩余航程Stogo不再减小为终止条件。
3.1 标准情况下再入制导仿真
为验证所提制导算法的有效性和自适应能力, 在目标点位置不变的情况下, 选取不同再入点进行再入过程仿真, 并与使用传统侧向制导方法的预测-校正制导再入仿真结果进行对比。
设再入初始状态如表 1所示。算例1~3的再入初始经、纬度不同, 到目标点的航程依次减小, 其他初始参数均相同。
再入初始状态
用侧向机动能力预测制导法、传统的航向角误差走廊侧向制导法和横程走廊侧向制导法分别以算例1~3的参数为初始状态进行再入制导仿真。航向角误差走廊参数设置为:当速度大于2 500 m/s时, 走廊边界值为20°; 当速度在2 500~7 00 m/s之间时, 走廊边界值由20°线性减小至5°; 当速度小于700 m/s时, 走廊边界值为5°。横程走廊参数设置为:当速度大于3 000 m/s时, 走廊边界值为4.3°; 当速度在3 000~2 000 m/s之间时, 走廊边界值由4.3°线性减小至0.3°; 当速度小于2 000 m/s时, 走廊边界值为0.3°。
侧向机动能预测制导法再入仿真结果见表 2, 图 2为再入纵向轨迹, 图 3为地面投影航迹曲线。航向角误差走廊制导法的再入仿真结果见表 3, 地面航迹如图 4所示。横程走廊制导法的再入仿真结果见表 4, 地面航迹如图 5所示。由表 2可以看出, 针对不同航程任务, 侧向机动能力预测制导法均能够将飞行器引导至目标点处, 不需要重新设计侧向走廊或人为调整侧向制导参数, 制导精度高, 最大落点误差小于5 km, 且落点精度稳定, 倾侧角反转3~4次, 相对较少; 表 3结果显示航向角误差走廊制导法的落点精度不稳定, 以算例1为初始状态再入时, 落点误差很小, 只有1.944 km, 但随着任务航程的减小落点误差反而增大, 算例2和算例3的落点误差分别达到了12.355 km和16.846 km, 且再入任务航程大时倾侧角反转次数多, 算例1反转7次, 明显高于侧向机动能力预测制导法算例1的4次; 由表 4可见横程走廊制导法无法胜任不同航程的再入任务, 在算例3的情况下落点误差达到400 km以上, 已无法飞向目标点位置, 如图 5中虚线所示。
侧向机动能力预测制导法仿真结果
航向角误差走廊制导法再入仿真结果
横程走廊制导法再入仿真结果
图 6给出了侧向机动能力预测制导法再入仿真3种算例的横程变化曲线, 其中实线表示再入横程, 点划线表示相应横程走廊边界。图 7是各算例再入过程中倾侧角变化曲线。算例1航程最大, 纵向制导将得出一条取值较小的倾侧角幅值曲线, 以满足纵向航程要求, 而较小的倾侧角幅值会减小升力侧向分量, 使飞行器侧向机动能力变弱, 因此由(23)式给出的横程走廊边界整体较小。反之, 算例3航程最小, 再入时倾侧角幅值较大, 飞行器侧向机动能力强, 走廊边界相对就大。横程走廊边界随剩余航程的减小而收缩。由仿真结果可知根据飞行器侧向机动能力动态调整的走廊边界能有效约束再入横程, 使飞行器飞向目标点时横程趋近于0。
 |
图2 侧向机动能力预测制导法再入高度-速度曲线 |
 |
图3 侧向机动能力预测制导法地面航迹曲线 |
 |
图4 航向角误差走廊制导法地面航迹曲线 |
 |
图5 横程走廊制导法地面航迹曲线 |
 |
图6 侧向机动能力预测制导法再入横程变化曲线 |
 |
图7 侧向机动能力预测制导法再入倾侧角变化曲线 |
3.2 扰动状态下再入制导仿真
为验证侧向机动能力预测制导法的抗干扰能力和鲁棒性, 分别对存在初始状态偏差和再入过程扰动的情况进行仿真。
3.2.1 初始状态偏差仿真
由于再入初始位置对制导的影响在3.1节已经讨论, 因此以表 1算例2的再入初始状态为基础, 仅考虑除经、纬度以外的参数偏差情况, 进行再入仿真。
仿真结果见表 5, 地面航迹曲线如图 8所示。由此可以看出, 对存在初始状态偏差的再入飞行情况, 侧向机动能力预测制导法具有良好且稳定的制导性能。
初始状态偏差再入仿真结果
 |
图8 初始状态偏差仿真地面航迹曲线 |
3.2.2 再入过程扰动仿真
考虑再入过程中大气密度、飞行器质量和升、阻力系数偏差的影响, 进行Monte Carlo仿真。仍以表 1算例2的参数为再入初始状态, 再入过程中, 大气密度偏差在±20%的范围内, 飞行器质量偏差为±5%, 升、阻力系数偏差均为±15%, 以上偏差均匀分布, 进行1 050次再入仿真计算。图 9为CAV-L再入航迹, 落点散布如图 10所示。结果表明, 最大落点误差为9.71 km, 圆概率误差(CEP)为4.53 km, 由此可见侧向机动能力预测制导法可靠有效。
以其中一次再入仿真为例, 实际再入大气密度为USSA-1976标准模型的90%, 纵向再入预测使用双参数指数大气模型作为标称值, CAV-L实际升力系数是标称值的105%, 阻力系数是标称值的95%。再入过程中对大气密度和CAV-L升阻比的在线参数估计结果如图 11和图 12所示。可以看出, 纵向制导时预测再入轨迹所用的大气密度和升阻比修正值均能较好贴近实际值, 保证轨迹预测精度。引入在线参数估计增强了预测-校正制导算法对再入过程扰动的鲁棒性。
 |
图9 再入过程扰动仿真航迹曲线 |
 |
图10 再入过程扰动仿真落点散布 |
 |
图11 大气密度在线修正 |
 |
图12 CAV-L升阻比在线修正 |
4 结论
针对高超声速飞行器再入问题, 在预测-校正制导法的基础上, 提出了一种根据侧向机动能力预测来实时改变横程走廊边界的侧向制导算法。仿真分析表明:
1) 依据预测的飞行器升力侧向分量均值调整横程走廊约束可以有效控制再入侧向运动, 引导再入飞行器飞向目标;
2) 该算法比数值预测搜索倾侧角反转时机的方法计算量要小, 比传统侧向误差走廊制导方法自适应能力要强;
3) 对再入初始状态和过程扰动均具有较好鲁棒性。
因而, 文中所提算法在适应不同航程任务需求, 保持制导精度稳定性方面具有一定参考价值, 能进一步增强预测-校正制导法的鲁棒性。
References
- Greg A D. Profile-Following Entry Guidance Using Linear Quadratic Regulator Theory[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, 2002 [Google Scholar]
- Curtis Z, Greg D, John H. An Automated Method to Compute Orbital Reentry Trajectories with Heating Constraints[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 523-529 [Article] [CrossRef] [Google Scholar]
- Wang Jinbo, Cui Naigang, Guo Jifeng, et al. High Precision Rapid Trajectory Optimization Algorithm for Launch Vehicle Landing[J]. Control Theory & Applications, 2018, 35(3): 389-398 [Article] (in Chinese) [Google Scholar]
- Hamel J F, Lafontaine J D. Improvement to the Analytical Predictor-Corrector Guidance Algorithm Applied to Mars Aerocpture[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 1019-1022 [Article] [CrossRef] [Google Scholar]
- Lu P. Entry Guidance:A Unified Method[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 713-728 [Article] [CrossRef] [Google Scholar]
- Wang Zhi, Tang Shuo, Yan Xiaodong. Constrained Predictor-Corrector Reentry Guidance for Hypersonic Glide Vehicle[J]. Flight Dynamics, 2012, 30(2): 175-180 [Article] (in Chinese) [Google Scholar]
- Liang Zixuan, Ren Zhang. Predictive Reentry Guidance with Aerodynamic Parameter Online Correction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7): 853-857 [Article](in Chinese) [Google Scholar]
- Wang Zhi, Zhang Ran, Li Huifeng. Hybrid Re-Entry Guidance for Reusable Launch Vehicle[C]//2014 Asia-Pacific International Symposium on Aerospace Technology, 2015: 999-1004 [Google Scholar]
- Song Jianshuang, Hu Yu, Hong Bei, et al. Predictor-Corrector Guidance for Common Aero Vehicle[J]. Missiles and Space Vehicles, 2016, 348(34): 38[Article] (in Chinese) [Google Scholar]
- Cheng Yang, Cheng Lin, Zhang Qingzhen, et al. Aircraft Predictor-Corrector Guidance Based on Online Constraint Limit Enforcement[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2143-2153 [Article] (in Chinese) [Google Scholar]
- Wang Qing, Ran Maopeng, Zhao Yang. Reentry Guidance for Hypersonic Vehicle Based on Predictor-Corrector Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12):1563-1567 [Article](in Chinese) [Google Scholar]
- Ran Maopeng, Wang Qing, Mo Huadong, et al. ANFIS-Based Predictive Reentry Guidance for Hypersonic Vehicles[J]. Acta Armamentarii, 2014, 35(12): 2016-2022 [Article] (in Chinese) [Google Scholar]
- Yong Enmi, Qian Weiqi, He Kaifeng. An Adaptive Predictor-Corrector Reentry Guidance Based on Self-Definition Way-Points[J]. Aerospace Science and Technology, 2014, 39:211-221 [Article] [CrossRef] [Google Scholar]
- Li Huifeng, Xie Ling. Reentry Guidance Law Design for RLV Based on Predictor-Corrector Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(11): 1344-1348 [Article](in Chinese) [Google Scholar]
- Zhao Jiang, Zhou Rui. Predictor-Corrector Reentry Guidance Based on Feedback Bank Angle Control[J]. Acta Armamentarii, 2015, 36(5): 823-830 [Article] (in Chinese) [Google Scholar]
- Shen Zuojun, Lu Ping. Dynamic Lateral Entry Guidance Logic[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 949-959 [Article] [CrossRef] [Google Scholar]
- Lu Ping. Predictor-corrector Entry Guidance for Low Lifting Vehicles[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, Hilton Head, South Carolina, 2007: 6425 [Google Scholar]
- Xue Songbai, Lu Ping. Constrained Predictor-Corrector Entry Guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281 [Article] [CrossRef] [Google Scholar]
- Guo Jifeng, Fu Yu, Cui Naigang. Three Dimensional Autonomous Entry Guidance Method[J]. Control and Decision, 2013, 28(5): 688-694 [Article] [Google Scholar]
- Wang Tao, Zhang Hongbo, Zhu Ruyi, et al. Predictor-Corrector Reentry Guidance Based on Drag Acceleration[J]. Journal of Astronautics, 2017, 38(2): 143-151 [Article] (in Chinese) [Google Scholar]
- Hu Zhengdong. Research on Trajectory Planning and Guidance for Space-Based Strike Weapon[D]. Changsha: National University of Defense Technology, 2009(in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 预测-校正制导逻辑框图 |
| In the text | |
 |
图2 侧向机动能力预测制导法再入高度-速度曲线 |
| In the text | |
 |
图3 侧向机动能力预测制导法地面航迹曲线 |
| In the text | |
 |
图4 航向角误差走廊制导法地面航迹曲线 |
| In the text | |
 |
图5 横程走廊制导法地面航迹曲线 |
| In the text | |
 |
图6 侧向机动能力预测制导法再入横程变化曲线 |
| In the text | |
 |
图7 侧向机动能力预测制导法再入倾侧角变化曲线 |
| In the text | |
 |
图8 初始状态偏差仿真地面航迹曲线 |
| In the text | |
 |
图9 再入过程扰动仿真航迹曲线 |
| In the text | |
 |
图10 再入过程扰动仿真落点散布 |
| In the text | |
 |
图11 大气密度在线修正 |
| In the text | |
 |
图12 CAV-L升阻比在线修正 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


