| Issue |
JNWPU
Volume 38, Number 1, February 2020
|
|
|---|---|---|
| Page(s) | 1 - 5 | |
| DOI | https://doi.org/10.1051/jnwpu/20203810001 | |
| Published online | 12 May 2020 | |
Attitude Calculation Based on Sequential Correction of Gravity Field and Geomagnetic Field
基于重力场与地磁场序贯修正的姿态解算研究
School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
Received:
13
March
2019
Aiming at the problems of gyroscope error divergence and magnetometer susceptibility to soft magnetic environment in attitude calculation of unmanned system, a method of attitude calculation based on gravity field and geomagnetic field sequential correction is proposed. In this method, gyroscope output is used to construct the state equation of attitude quaternion, and then the quaternion is sequentially corrected twice by using accelerometer and magnetometer data in order to obtain accurate attitude output. The experimental results show that, compared with the three traditional attitude calculation algorithms, this algorithm can effectively suppress the gyroscope drift error and improve the attitude output accuracy under the environment of magnetic interference. The static accuracy of the attitude angle is not greater than that of the dynamic accuracy, which meets the application requirements of the unmanned system.
摘要
针对无人系统姿态解算中存在陀螺仪误差发散快、磁力计易受软磁环境干扰等问题,提出了一种基于重力场与地磁场序贯修正的姿态解算方法。该方法采用陀螺仪输出构建姿态四元数的状态方程,然后依次利用加速度计与磁力计数据对四元数进行2次序贯修正,以获得姿态的准确输出。实验结果表明,相比传统的2种姿态解算算法,新算法能有效抑制陀螺仪的漂移误差,提高磁干扰环境下的姿态输出精度,其姿态角的静态精度不大于0.5°,动态精度优于2°。
Key words: earth gravity field / geomagnetic field / sequential kalman filter algorithm / attitude calculation
关键字 : 地球重力场 / 地磁场 / 序贯卡尔曼滤波算法 / 姿态解算
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
无人系统的姿态解算是导航领域研究的重点内容之一,它的本质是对惯性传感器数据的融合计算过程。目前较为有效的做法是:通过读取多个MEMS传感器的实时数据,利用滤波算法对数据进行融合,解算得到载体的3个姿态信息[1]。
航姿系统虽然具有成本低、体积小和集成度高等优点,但是仍然存在陀螺仪温漂比较严重、加速度计输出噪声过大以及磁力计易受周围磁场干扰等问题[2-3],导致载体姿态测量解算存在偏差。针对上述问题,国内外学者已经提出了多种姿态解算方法来提高姿态控制精度。文献[4]提出了基于传统卡尔曼滤波的姿态估计方法,并对动态条件下的外部加速度进行了补偿。文献[5]提出了基于四元数的扩展卡尔曼滤波算法,并借助三轴飞行转台进行了实验验证,算法中忽略了软磁干扰对磁测量及姿态解算的影响。文献[6]采用互补滤波器对IMU和磁力计数据进行融合,降低了姿态解算的计算量,提高了运算效率。文献[7]将陀螺偏差和磁扰动作为状态矢量进行补偿,提高了静态精度。文献[8]提出了基于矢量测量的卡尔曼滤波算法,有效地降低了动态系统的量测噪声。
本文在前人研究的基础上,针对:①姿态角存在累积误差;②航向姿态输出噪声过大、姿态解算精度降低等问题,提出了一种基于重力场与地磁场序贯修正的姿态算法。首先,依据陀螺仪的输出得到姿态四元数;然后,使用MEMS传感器采集的载体重力加速度与载体地磁场矢量依次对四元数进行2次修正,以此实现载体姿态的估计。该方法能有效抑制陀螺仪的漂移,降低磁干扰对航向姿态的影响,具有较高的精度。最后,利用搭建的XQ-4 ROS移动机器人平台对本算法进行了实验验证。
1 姿态解算问题描述
假设q为从载体系B到全局系G的四元数, 利用四元数微分方程表示陀螺仪动力学模型
式中, ωGBB是利用陀螺仪在载体系下直接测得的角速度, 其矩阵形式为ω=[ωxωyωz]T。
本文主要针对MEMS传感器的零位偏差和随机漂移误差进行补偿。建立相应的误差模型如下:
1) 陀螺仪输出模型
式中: ω为陀螺仪实际输出的角速度值; ω°为载体角速度理想真值; δg为陀螺仪的零位偏差; vg为零均值的高斯白噪声。
2) 加速度计输出模型
在载体系B下, 加速度计测量的矢量a, 全局系G下的地球重力加速度矢量Gg表示如下
加速度计输出模型可以表示为
式中: a为加速度计实际测量值; Bg为重力加速度在载体系上的投影; a°为载体理想的加速度真值; δa, va分别为加速度计的零位偏差和零均值高斯白噪声。
3) 磁力计输出模型
类似的, 在载体系B下, 定义磁力计测量的地磁场矢量为m, 全局系G下的真实地磁场矢量为h, 二者可以表示为
磁力计输出模型可以表示为
式中: m为磁力计实际测量值; Bh为全局系地磁场矢量在载体系上的投影; m′为载体自身材料的磁场分量; δm为磁力计的零位偏差; vm为零均值的高斯白噪声。
2 序贯卡尔曼滤波器设计
本节利用重力场与地磁场信息依次对姿态四元数进行2次序贯最优估计, 对于加速度计和磁力计, 分别建立各自对应的观测方程, 为
式中: Hgk和Hmk分别为加速度计量测矩阵和磁力计量测矩阵; Vgk和Vmk分别为加速度计量测噪声向量和磁力计量测噪声向量。
2.1 系统状态方程
选取姿态四元数作为状态变量, 在(1)式中, 用角增量代替角速度确定四元数, 同时通过四元数微分方程的毕卡求解法, 将(1)式离散化, 记为
式中, qk为tk时刻全局系G到载体系B的旋转四元数。
系统状态方程可以表示为
根据(3)式建立的陀螺仪误差模型以及文献[8]的附录A, 在微小的时间间隔Δt内, 将上式中的 可以改写为
可以改写为
由于姿态四元数qk与δg噪声相互独立,系统的噪声协方差矩阵Qk可以表示为
式中,Σg为陀螺仪噪声协方差矩阵,有Σg=δgg(δg)T。
2.2 加速度计观测模型
将B系和G系下的加速度矢量a和g分别转换为零标量的四元数a和g,利用离散化的四元数qk表示二者的转换关系,为
同样地,加速度计量测矩阵Hgk0记为
加速度计的量测噪声协方差矩阵Rgk为
式中,Σa=δag(δa)T为加速度计噪声协方差矩阵。
重力加速度修正的卡尔曼滤波增益Kgk为
加速度计观测模型修正后的四元数状态估计为
2.3 磁力计观测模型
本节利用磁力计和四元数后验状态估计,对姿态四元数进行2次修正。
磁力计伪观测模型为
式中:磁力计量测矩阵 ;磁力计量测噪声矩阵
;磁力计量测噪声矩阵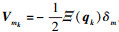 。
。
利用加速度计观测模型更新后的四元数 ,替换(17)式中的四元数qk,则磁力计的量测噪声协方差矩阵Rmk可以表示为
,替换(17)式中的四元数qk,则磁力计的量测噪声协方差矩阵Rmk可以表示为
式中,Σm为磁力计噪声协方差矩阵。
地磁场矢量修正的卡尔曼滤波增益Kmk为
磁力计第2次修正后的四元数估计为
利用磁力计观测模型修正后得到的四元数状态估计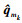 继续作为k-1时刻的四元数,返回到陀螺仪系统模型中,即
继续作为k-1时刻的四元数,返回到陀螺仪系统模型中,即
3 实验验证分析
以XQ-4 ROS移动机器人为载体平台, 以AH-100B为姿态传感器, 进行了静态、动态测试实验。AH-100B系统集成了3种MEMS器件, 各器件精度指标:三轴陀螺仪的误差均方差为0.1°/s, 三轴加速度计误差均方差为5 mg, 三轴磁力计误差均方差为2.5 mgauss。
3.1 静态试验验证
序贯滤波器相关参数设置如下:初始均方误差矩阵P0=I4×4;状态向量初值q0=[1 0 0 0]T;陀螺仪噪声协方差矩阵Σg=0.08×[I3×3];加速度计噪声协方差矩阵Σa=0.02×[I3×3];磁力计噪声协方差矩阵Σa=0.3×[I3×3]; βa=0.02;βm=0.03。
实验过程中始终保持载体处于静止状态,将系统置于水平台上, 其航向角静态基准角1.82°, 实验过程始终保持MEMS系统处于静止状态, 采集2 h实验数据。将SEKF解算结果与二阶互补滤波(CF)、自适应卡尔曼滤波(AEKF)的姿态结果进行对比, 三者航向角与真值之间的误差输出曲线如图 1所示。
通过图 1可以看出, 在静态条件下, 对于载体航向角, 互补滤波算法的误差范围接近2°, 且呈发散状态; 自适应卡尔曼滤波器的航向角误差虽然在±1°范围内且无累积误差, 但是输出曲线中包含较多噪声; 相比之下, 序贯卡尔曼滤波算法解算姿态更为准确, 航向角误差范围在±0.5°以内, 输出曲线较为平滑。
为定量分析3种滤波算法的静态精度, 在2 h采样时间内, 分别计算3种滤波器的航向角平均误差, CF、AEKF及SEKF分别为:1.436°, 0.645°及0.358°。相比于CF和AEKF算法, SEKF输出的航向角精度更高。通过图 1可知, 在2 h运行期间, 本文所提出的SEKF算法航向误差处于稳定范围0.3°, 表明系统具备长时间工作的能力, 且静态解算精度较高。
 |
图 1 3种滤波算法航向角误差曲线对比 |
3.2 动态试验验证
实验前, 预先在地面进行几何标定, 实验区域为正方形(3.2 m×3.2 m), 场景如图 2a)所示。实验步骤如下:
1) 控制ROS机器人沿着黑边正方形轨迹运动, 逆时针方向运动5圈;
2) 利用ROS可视化工具Rviz实时绘制机器人运动轨迹, 如图 2b)所示;
3) 实时同步采集航姿系统输出数据, 截取第3圈车载实验航向姿态数据, 绘制姿态估计曲线与动态基准航向曲线, 如图 3所示。
由图 3可知, 在载体运动状态下, 3种滤波算法解算输出的航向角与动态基准航向角吻合较好, 均具备良好的动态跟踪效果。
对于载体的全部5圈动态实验, 将3种滤波算法解算的航向角与动态基准航向角做差, 其航向角误差曲线如图 4所示。
根据图 4可以看出, 互补滤波器航向角误差范围为±5°, 且逐渐发散; 自适应卡尔曼滤波算法的航向角误差为±3°以内, 但其滤波效果不够平滑; 序贯卡尔曼滤波器的航向角误差范围为±2°。分别计算3种算法的动态航向角平均误差和标准差, 如表 1所示。
通过表 1可知, 相比于互补滤波算法与自适应卡尔曼滤波算法, 序贯滤波器的动态航向角解算精度约为1.7°, 其标准差为1.124, 表明SEKF滤波的稳定性更好。由以上分析可知, 本算法在运动状态下解算姿态仍具有较高的精度, 累积误差较小, 证明了其具有良好的动态性能。
 |
图 2 XQ-4 ROS机器人动态实验运动轨迹图 |
 |
图 3 不同滤波算法动态航向姿态曲线图 |
 |
图 4 3种滤波算法动态航行角误差曲线 |
不同滤波算法动态性能比较
4 结论
本文针对传统姿态解算算法中存在的陀螺漂移严重、磁力计测量易受干扰等问题, 提出了一种基于重力场与地磁场序贯修正的姿态解算算法。该算法以陀螺仪采集的角速率更新得到姿态四元数, 然后依次利用加速度计和磁力计对四元数进行2次序贯修正, 降低了磁干扰对姿态解算的影响。实验结果表明, 本算法有效地修正了航姿系统的累计误差。
References
- Zhang Xiaojun, Xu Zihan, Yang Shipeng. Robot Attitude Calculation Algorithm Research[J]. Mechanical Design and Manufacturing, 2018, 328(6): 253–256 [Article] [Google Scholar]
- Li Rong, Li Zhe. Attitude Angle Solution Based on Indoor Positioning of MEMS[J]. Computer and Digital Engineering, 2017, 45(12): 2379–2382 [Article] [Google Scholar]
- Abbate N, Basile A, Brigante C, et al. Modern Breakthrough Technologies Enable New Applications Based on IMU Systems[J]. Journal of Sensors, 2011, 2011: 1–7 [Article] [CrossRef] [Google Scholar]
- Lee J K, Park E J, Robinovitch S N. Estimation of Attitude and External Acceleration Using Inertial Sensor Measurement During Various Dynamic Conditions[J]. IEEE Trans on Instrumentation and Measurement, 2012, 61(8): 2101–2109 [Article] [Google Scholar]
- Sheng Hanlin, Zhang Tianhong, Liu Dongdong. Design of Low Cost Attitude and Heading System Based on Extended Kalman Filter[J]. Systems Engineering and Electronic Technology, 2013, 35(10): 2158–2164 [Article] [Google Scholar]
- Sun Jinqiu, You Youpeng, Fu Zhongyun. Attitude Resolution Algorithm Based on Conjugate Gradient Method and Complementary Filtering[J]. Journal of Sensing Technology, 2014, 4: 524–528 [Article] [Google Scholar]
- Sabatini Maria A. Variable-State-Dimension Kalman-Based Filter for Orientation Determination Using Inertial and Magnetic Sensors[J]. Sensors, 2012, 12(12): 8491–8506 [Article] [CrossRef] [Google Scholar]
- Choukroun D, Bar-Itzhack I Y, Oshman Y. Novel Quaternion Kalman Filter[J]. IEEE Trans on Aerospace and Electronic Systems, 2006, 42(1): 174–190 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Roberto V, Ivan D, Xu Jizhong. Keeping a Good Attitude:A Quaternion-Based Orientation Filter for IMUs and MARGs[J]. Sensors, 2015, 15(8): 19302–19330 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 3种滤波算法航向角误差曲线对比 |
| In the text | |
 |
图 2 XQ-4 ROS机器人动态实验运动轨迹图 |
| In the text | |
 |
图 3 不同滤波算法动态航向姿态曲线图 |
| In the text | |
 |
图 4 3种滤波算法动态航行角误差曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


