| Issue |
JNWPU
Volume 38, Number 1, February 2020
|
|
|---|---|---|
| Page(s) | 6 - 13 | |
| DOI | https://doi.org/10.1051/jnwpu/20203810006 | |
| Published online | 12 May 2020 | |
MIMO Sonar DOA Estimation with Joint Matched-Filtering Based on Transmission Diversity Smoothing
联合匹配滤波MIMO声呐发射分集平滑DOA估计方法
School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
Received:
16
April
2019
There is a class of methods based on transmission diversity smoothing by multiple-input multiple-output(MIMO) sonar called MIMO-TDS which is considered as one of the most effective methods for estimation of direction-of-arrival(DOA) using MIMO sonar systems. MIMO-TDS produced by orthogonal signal transmission for active sonar can be immediately implemented with high resolution algorithms such as MVDR to estimate the direction of received signals. However, the orthogonal transmission mode of MIMO-TDS is doomed to a loss of transmission array gain indirectly leading to the problem that the echoes are not equipped with as high SNR as enough for an accurate target localization, especially in scenarios in which the targets are far away from array. In order to solving the "low SNR" problem, a solution using all transmitted signals simultaneously to design a joint matched-filter intended for received signal is proposed to improve the performance of MIMO-TDS, which is inspired by the match-filtering concept of "MIMO sonar virtual array method" simplified as MIMO-VA. And accordingly, the unit impulse response function of proposed joint matched-filter is the equivalent of linear sum of all orthogonal transmitted signals and the modified MIMO-TDS is named as "joint matched-filtering MIMO sonar transmission diversity smoothing DOA estimation method", which could be simplified as MIMO-TDS-MF. The characteristic of proposed method is analyzed theoretically and compared to MIMO-TDS and MIMO-VA in this paper:Compared with MIMO-TDS, the proposed method not only retains the advantage of transmission diversity smoothing but also improves the SNR by joint match-filtering; What's more, compared with MIMO-VA, MIMO-TDS-MF is equipped with substantially less computation than the former due to an employment of much fewer matched-filters and is in possession of a superior robustness to that of MIMO-VA. Numerical experiments demonstrate the efficiency of proposed MIMO-TDS-MF.
摘要
MIMO声呐发射分集平滑(transmission diversity smoothing,TDS)法(简称为MIMO-TDS)是一类重要的多输入多输出(multiple-input multiple-output,MIMO)声呐DOA估计方法。该方法利用发射正交波形来获得发射分集平滑特性,保证了MVDR等自适应高分辨算法的直接应用,但也因此牺牲了发射端的阵增益,在对较远距离的目标进行探测定位时,该方法常会面临回波信噪比不足、性能损失严重等问题。针对该缺点,借鉴了MIMO声呐虚拟阵列(virtual array,VA)法(简称为MIMO-VA)中的匹配滤波思想,提出同时利用所有发射信号对回波进行联合匹配滤波处理的方式提高信噪比,该联合匹配滤波器的单位脉冲响应函数由所有正交发射信号经线性叠加构成。研究表明,所提出的匹配滤波器不仅能够提高接收信噪比,改善MIMO-TDS在低信噪比条件下的性能,还保留了MIMO声呐的发射分集平滑特性。与MIMO-VA相比,所提方法大幅减少了所需匹配滤波通道数量,具有较低的运算量;且存在发射阵列流形误差、发射信号同步误差时,具有更优的稳健性。利用计算机仿真对所提方法的有效性进行了验证。
Key words: MIMO sonar / DOA estimation / match-filtering / transmission diversity smoothing / numerical experiment
关键字 : MIMO声呐 / 目标方位估计 / 匹配滤波 / 发射分集平滑
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
目标方位(direction-of-arrival, DOA)估计是水声信号处理中一项重要研究内容[1]。传统的单输入多输出(single-input multiple-output, SIMO)声呐在提高方位分辨能力时,通常采用增加阵元个数、扩大阵列孔径的方法[2-3],而这往往会带来尺寸过大不易搭载、系统成本过高等问题。为了突破传统SIMO声呐在提高方位分辨能力上所遇到的瓶颈,多输入多输出(multiple-input multiple-output, MIMO)技术被应用到声呐系统上[4-8]。MIMO声呐采用多个正交波形作为发射信号,有利于降低多目标回波之间的信号相关性,可直接应用高分辨DOA估计算法(如MVDR、MUSIC等)进行方位估计;同时,结合接收端的匹配滤波处理可获得大孔径虚拟阵,突破传统SIMO声呐的孔径限制[4-6]。结合上述2个主要特性,已有的MIMO声呐DOA估计方法分为2种:①MIMO声呐发射分集平滑(transmitting spatial smoothing, TDS)法(简称为MIMO-TDS),该方法中当发射阵元个数大于等于目标个数时,来自多目标的回波能自动解相干[5-6, 9],可以直接运用高分辨算法进行方位估计,避免了划分子阵所引起的孔径损失问题,但是MIMO-TDS在低信噪比下的DOA估计性能较差。②MIMO声呐虚拟阵列(virtual array, VA)法(简称为MIMO-VA),该方法利用发射信号分别对阵元回波信号进行匹配滤波处理,通过匹配滤波输出构造大孔径虚拟阵列再进行DOA估计[10-12],具有较高的分辨率,尤其在低信噪比时DOA估计性能突出。但是,为了将虚拟阵列的孔径最大化,MIMO-VA必须配合特殊的阵形设计,且虚拟阵列的构造需要精确的发射阵阵列流形,因此,该方法的实际性能对发射阵列流形误差(信号同步误差、发射阵元位置误差等)较为敏感。其次,大量匹配滤波器的使用导致MIMO-VA存在运算量过大的问题[13]。
MIMO-VA对阵列流形的精确度有较高的要求,存在误差时稳健性差,实际应用存在较大困难。据此,本文着力于对MIMO-TDS的改进,针对其低信噪比条件下DOA估计性能差的问题,提出联合匹配滤波MIMO声呐发射分集平滑DOA估计法(MIMO-TDS-MF)。所提方法借鉴MIMO-VA中利用匹配滤波器提高信噪比的思想,先对接收信号进行匹配滤波处理,再进行高分辨DOA估计。区别于MIMO-VA分别利用单个发射信号进行多次“匹配滤波分选”来获得大孔径虚拟阵列,MIMO-TDS-MF采用的是多个发射信号联合匹配滤波的处理方式,该方式旨在使用匹配滤波处理提高信噪比的同时,保证匹配滤波输出仍具有良好的发射分集平滑特性,进而不影响高分辨DOA估计算法的直接应用。本文针对MIMO声呐的低信噪比DOA估计问题,对联合匹配滤波MIMO声呐发射分集平滑DOA估计法的性能进行验证,并结合MIMO-TDS、MIMO-VA分析研究所提方法的稳健性及运算效率,仿真验证所提方法的有效性。
1 MIMO声呐信号模型和DOA估计方法
1.1 MIMO声呐信号模型
假设MIMO声呐的收发阵列同为均匀线列阵(uniform linear array, ULA), M元发射ULA和N元接收ULA布放于同一条直线上, 阵列的信号发射和接收模型如图 1所示。图 1中, 实心圆表示发射阵元, 不同的线型表示各阵元发射相互正交的信号, 空心圆表示接收阵元。
在该模型中, 假设目标处于发射/接收阵的远场。由于发射/接收阵位于同一条直线上, 第p个目标到MIMO声呐的各个发射、接收阵元的角度相同, 记为θp(目标与基阵法线的夹角)。为简化分析, 忽略回波的多普勒频移以及扩散损失和介质吸收损失, 仅考虑目标散射强度对回波强度的影响。因此, N元接收阵上的回波信号x(t)可以表示为[5, 14]
式中: s(t)=s1(t)s2(t)…sM(t)T为发射ULA上M个相互正交的发射信号所构成的信号向量, 发射信号之间的相关系数ρik满足如下关系
式中: []*表示取共轭, (1)式中的at(θp)和ar(θp)分别为发射ULA和接收ULA的阵列流形向量
式中: f0是发射信号的中心频率, dt, dr分别是发射阵和接收阵的阵元间距。βp是第p个目标的散射强度, z(t)为接收阵元上的加性高斯白噪声向量。
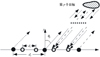 |
图 1 MIMO声呐信号模型 |
1.2 MIMO声呐发射分集平滑法(MIMO-TDS)
MIMO-TDS法直接利用(1)式中的回波信号x(t)构造协方差矩阵RTDS
接收阵的基阵扫描向量aTDS(θ)可表示为
根据(5)和(6)式, 直接获得MIMO-TDS下的MVDR空间谱
MIMO-TDS的核心在于利用MIMO声呐的发射分集平滑特性保证不同目标的回波自动相互解相干[10-11], 即回波信号所组成的向量组是线性无关的。当利用MVDR、MUSIC等高分辨算法进行DOA估计时, 该特性可避免空间平滑所引起的阵列有效孔径损失问题, 并且其简洁的回波处理过程具有低运算量的特点。但是, 该方法在低信噪比条件下DOA估计性能下降严重。
1.3 MIMO声呐虚拟孔径法(MIMO-VA)
MIMO-VA在接收端用M个发射信号的拷贝对N个接收阵元上的回波分别进行匹配滤波, 获得M×N个输出[4]。第(m-1)N+n个输出可以表示为
式中, hm(t)是与第m个发射信号相对应的匹配滤波器的冲击响应函数
式中, T为发射信号的脉宽。根据等效虚拟阵列理论, 可以认为输出y(m-1)N+n(t)即为虚拟SIMO声呐上第(m-1)N+n号接收阵元上经脉冲压缩后的回波。则虚拟SIMO声呐的接收阵阵列流形即扫描向量可以表示成MIMO声呐发射与接收阵列流形的直积
通过M×N个匹配滤波输出可得到虚拟SIMO阵的回波向量
MIMO-VA的基阵输出协方差矩阵RVA可以表示为
最后可以获得MIMO-VA的MVDR空间谱
MIMO-VA在处理回波时共进行M×N次匹配滤波, 提高信噪比的同时也显著增加了系统的计算量。此外, 由(10)式可知, 虚拟阵列的构造不仅需要接收阵列流形, 还需要精确的发射阵列流形信息, 当存在发射阵列流形误差时, 该方法会面临阵列流形失配所导致的高分辨DOA估计算法性能急剧下降的问题。
2 联合匹配滤波MIMO声呐发射分集平滑法
MIMO-TDS-MF的核心是联合匹配滤波处理, 旨在保留MIMO-TDS发射分集平滑特性的前提下, 通过匹配滤波改善信噪比。观察图 1中MIMO声呐的信号模型和(1)式, 将第n号接收阵元上的信号xn(t)重写成如下形式
式中: ϕr, p=2πf0drsin(θp)/c及ϕt, p=2πf0dtsin(θp)/c, zn(t)是单个阵元上的加性噪声。显然, 如果除去噪声成分, 则单个阵元上的接收信号本质上是M个正交发射信号经不同的相位、幅度调制之后作线性叠加所构成, 这正是MIMO声呐发射分集平滑特性的来源。鉴于此, 设计如下的匹配滤波器, 其单位脉冲响应函数为
式中: T为发射信号的脉宽, 整个脉冲响应函数由发射信号作共轭、时域翻转及延迟处理之后线性叠加获得, 该设计方式可以完整的保留输入端的所有信号成分, 本文称这种匹配滤波方式为联合匹配滤波。以第n号阵元的接收信号xn(t)为例, 经(15)式的匹配滤波器处理之后获得的输出信号是
利用y(t)=y1(t)y2(t)…yN(t)T构造MIMO-TDS-MF的N×N维输出协方差矩阵RTDS-MF
所提方法的基阵扫描向量aTDS-MF(θ)与MIMO-TDS的相同
最后获得MIMO-TDS-MF的MVDR空间方位谱
由于发射信号之间相互正交, (16)式中匹配滤波输出信号yn(t)的主要成分相当于是各个正交发射信号自相关输出的线性叠加, 且相互之间仍保持良好的正交性。因此, MIMO-TDS-MF所采用的联合匹配滤波处理方式在提高信噪比的同时, 仍保留了MIMO-TDS中良好的发射分集平滑特性, 还是可以直接利用高分辨算法进行DOA估计。
运算量大小是衡量方法优劣的一项重要指标。结合MIMO-TDS-MF和2种已有方法的回波处理过程, 表 1将影响方法计算速度的几项重要运算参数进行了对比。
根据表 1可知, 由于匹配滤波器的使用, 所提方法相较于MIMO-TDS增加了一定的计算量。不同于MIMO-VA通过构造大孔径虚拟阵来进行方位估计, MIMO-TDS-MF的整个DOA估计过程中仍基于MIMO声呐原始接收阵列。因此相较于MIMO-VA, MIMO-TDS-MF在协方差矩阵维度、扫描向量维度、匹配滤波次数等运算参数的比较上, 具有明显的优势。
运算参数对比
3 仿真实验及结果分析
数值仿真过程中, MIMO声呐分别采用阵元个数M=5的发射LA和阵元个数N=8的接收ULA, 收、发阵列布置于同一条直线上且两者的几何中心相互重合, 接收阵元间距dr=λ/2(λ根据发射信号中心频率确定即λ=c/f0), 发射阵元间距dt=Ndr, 发射阵列采用稀疏布阵方式[14]。图 2为MIMO声呐的阵列示意图。
发射信号采用5个时域相互正交的单频矩形脉冲(CW)信号。为了保证发射信号之间具有良好的正交性, 设置相邻单频脉冲信号中心频率的频偏Δf=200 Hz, 整个工作频带的中心频率f0=15 kHz。信号采样频率Fs=3f0, 快拍数L=4 096。设接收阵元上的加性噪声为窄带高斯白噪声, 噪声频带范围限制在(14.4~15.6)kHz, 采用频带级信噪比, 水中声速c=1 500 m/s。
本节根据上述的仿真参数, 结合MIMO-TDS和MIMO-VA作对比验证, 通过多组数值仿真实验分别分析了MIMO-TDS-MF在低信噪比条件下和发射端存在误差时的DOA估计性能, 仿真实验过程中均采用MVDR作为DOA估计算法。
 |
图 2 MIMO阵列示意图 |
3.1 低信噪比下MIMO-TDS-MF的DOA估计性能
该组实验主要验证低信噪比下MIMO-TDS-MF的DOA估计性能, 仿真中假设不存在任何信号同步误差、阵列误差, 由于MIMO-VA在构造虚拟孔径过程中会丢失发射分集平滑特性, 仍需配合空间平滑来对阵元输出作解相干处理。图 3a)给出了单次方位估计的空间谱, 假设存在4个固定目标, 方位角度依次是-45°, -30°, 0°和15°, 归一化的目标强度βp依次为1, 0.5, 1和1, 信噪比RSN=0 dB, 根据15°处的目标信号强度添加噪声。图 3b)分析了MIMO-TDS-MF在不同信噪比下, 针对0°和15°处的2个目标, 进行多次蒙特卡罗实验后的成功分辨概率, 并和MIMO-TDS及MIMO-VA进行对比, 其中相同信噪比下的蒙特卡罗重复实验次数为1 000。
对于某次实验, 如果2个目标方位的估计值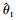 和
和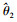 与真实值θ1及θ2之间满足
与真实值θ1及θ2之间满足
则认为该次实验能够成功分辨这2个目标, 成功分辨概率指正确分辨次数占重复实验次数的百分比。
图 3a)中的4个目标分成2组, -45°和-30°作为一组非等强度目标, 0°和15°作为一组等强度目标。显然, 低信噪比条件下MIMO-TDS的DOA估计性能较差, 对于方位差较小的非等强度目标, 该方法已经完全失效; 而本文所提出的MIMO-TDS-MF和已有的MIMO-VA由于匹配滤波器的使用获得了信噪比增益, 都做出了准确的方位估计。观察图 3b)同样可以发现, 相较于MIMO-TDS, 在-25~-5 dB这段区间内MIMO-TDS-MF的性能明显优于前者; 而由于等效大孔径虚拟阵的构造, 在理想条件下MIMO-VA的分辨性能全局最优, 但该方法仍需进行空间平滑。
 |
图 3 低信噪比下MIMO-TDS-MF的方位估计性能 |
3.2 存在发射阵列流形误差时MIMO-TDS-MF的DOA估计性能
仿真实验通过设置随机阵元位置扰动来构造发射阵列流形误差, 单次实验中对发射阵列添加一个M维随机扰动向量Δd=[Δd1Δd2…ΔdM]T, 其中Δd1, Δd2…ΔdM分别是M个发射阵元沿阵列水平方向的随机位置扰动, 每个随机误差量Δdm(m=1, 2…M)都服从均值为0、均方根误差为ERMS(Δd)的均匀分布, 彼此相互独立。本节仿真采用的信噪比RSN=-10dB, 2个等强度目标分别在0°和15°方向。
图 4a)描述了随着阵元位置扰动Δd的均方根误差的增大, MIMO-TDS-MF的多目标分辨性能变化规律。在相同的均方根误差扰动下, 分别进行1 000次蒙特卡罗重复实验, 判定是否成功分辨2个目标的准则同上。观察图 4a)可知, MIMO-TDS和本文提出的MIMO-TDS-MF的分辨性能几乎不随发射阵列流形误差的影响且MIMO-TDS-MF的成功分辨概率在低信噪比条件下一致优于MIMO-TDS, 由于虚拟阵列的构造需要精确的发射阵列流形, MIMO-VA的分辨性能则随着扰动的增大下降严重。均方根误差ERMS(Δd)=0.15λ时, 从1 000次实验中抽取某次DOA估计空间谱和前100次空间谱进行观察分析, 分别如图 4b)至4e)所示。其中MIMO-TDS分辨能力较差; MIMO-VA则由于误差扰动, 性能起伏大, 且存在严重的伪峰干扰, 影响系统判决; MIMO-TDS-MF兼顾分辨能力和稳健性, 表现良好。综上, 当存在发射阵列流形误差时, 在低信噪比条件下MIMO-TDS-MF的性能最优。
 |
图 4 存在发射阵列流形误差时的DOA估计性能 |
3.3 存在发射信号同步误差时MIMO-TDS-MF的DOA估计性能
在实际应用中, MIMO声呐的发射信号之间往往存在时间同步误差。数值仿真时对每个发射信号添加随机的时延扰动作为同步误差, M维随机时延扰动向量Δt=[Δt1Δt2…ΔtM]T, Δtm(m=1, 2…M)是第m个发射阵元上的信号时延, 服从均值为0、均方根误差为ERMS(Δt)的均匀分布, 彼此相互独立。假设存在2个等强度目标分别位于0°和15°方向, 信噪比RSN=-10 dB。
图 5a)给出了MIMO-TDS-MF的多目标分辨性能受发射信号同步误差影响的变化规律。同样, 在相同的均方根误差扰动下, 进行1 000次的蒙特卡罗重复实验, 对分辨成功的概率进行数值统计, 判决规则同3.1节。观察图 5a)可知, 随着时间同步误差的增加, MIMO-TDS-MF的分辨性能十分稳定, 信噪比较低时分辨概率一致优于MIMO-TDS; 由于虚拟阵列的构造, MIMO-VA稳健性较差, 少量的时延扰动使该方法的估计性能急剧下降。时延扰动的均方根误差ERMS(Δt)=2×10-5s时, 在1 000次实验中抽取某次DOA估计空间谱和前100次空间谱进行观察分析, 分别如图 5b)至5e)所示。同上, MIMO-TDS的谱估计结果旁瓣较高、主瓣较宽, 分辨性能差; MIMO-VA则完全失效, 无法进行估计; MIMO-TDS-MF则在分辨能力和稳健性上均表现良好。综上, 当存在发射信号的同步误差时, 在低信噪比条件下本文提出的MIMO-TDS-MF的性能最优。
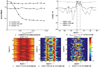 |
图 5 存在发射信号同步误差时的DOA估计性能 |
3.4 运算量分析
实际应用中,DOA估计方法的运算量是一项非常重要的技术指标,运算耗时的长短意味着算法在运行过程中所占用的计算资源的大小。下面对MIMO-TDS、MIMO-VA、MIMO-TDS-MF这3种方法的运算时间进行仿真对比,图 6是在相同的硬件条件下重复进行多次DOA估计的耗时曲线。该组实验中使用的计算机CPU是Intel(R)Core(TM)i5-4590,主频3.3 GHz,内存8 G,运行环境为win7下的MATLAB 2015b。
该实验给出的100次运行耗时曲线证明:MIMO-TDS的运行时间最短,本文提出的MIMO-TDS-MF次之,MIMO-VA需要的运算耗时则远大于前2种方法。结合表 1中3种方法的运算参数对比我们发现,相较于MIMO-TDS,MIMO-TDS-MF确实增加了一定数量的匹配滤波器,导致后者的运算时间稍高于前者。而与MIMO-VA进行比较,MIMO-VA的基阵输出协方差矩阵维度、扫描向量维度以及匹配滤波器的个数都要远高于本文提出的MIMO-TDS-MF。综上,MIMO-TDS-MF在运算耗时上具有一定的优势。
 |
图 6 基于MVDR 3种估计方法运行100次的耗时曲线 |
4 结论
本文在MIMO声呐的基础上,讨论了已有的2种DOA估计方法(MIMO-TDS和MIMO-VA)的优缺点。针对MIMO-TDS低信噪比条件下DOA估计性能下降严重的问题,结合MIMO-VA中的匹配滤波思想,对MIMO-TDS法进行改进,提出了一种联合匹配滤波MIMO声呐发射分集平滑DOA估计方法。相较于MIMO-TDS,所提方法通过匹配滤波获得了信噪比增益,提高了MIMO声呐的DOA估计性能,在低信噪比条件下优势明显,同时也保留了发射分集平滑这一优良特性;和MIMO-VA相比,存在发射阵列流形误差、发射信号同步误差时,MIMO-TDS-MF的稳健性远优于前者,同时MIMO-TDS-MF由于其发射分集平滑的特性,可以直接使用MVDR等高分辨算法,MIMO-VA仍需要空间平滑来对信号进行解相干;在运算量上,MIMO-TDS-MF为了获得更优的信噪比进行匹配滤波处理,相较于MIMO-TDS增加了一定的运算量,但对于MIMO-VA具有较大优势。综上,本文提出的联合匹配滤波MIMO声呐发射分集平滑DOA估计方法(MIMO-TDS-MF),在实际应用中性能更优。
References
- Li Qihu. Sonar Signal Processing Theory[M]. Beijing: Science Press, 2012 (in Chinese) [Google Scholar]
- Sun Chao. Underwater Multi-Sensor Array Signal Processing[M]. Xi'an: Northwestern Polytechnical University Press, 2007 (in Chinese) [Google Scholar]
- Van Trees H L. Optimum Array Processing:Part Ⅳ of Detection, Estimation and Modulation Theory[M]. New York, NY, USA: John Wiley & Sons, 2002 [Google Scholar]
- Sun Chao, LIU Xionghou. MIMO Sonar:Concept and Technical Characteristic Discuss[J]. Technical Acoustics, 2012, 31(2): 117–124 [Article] (in Chinese) [Google Scholar]
- Li J, Stoica P. MIMO Radar Signal Processing[M]. Hoboken, NJ, USA: Wiley-IEEE Press, 2008 [CrossRef] [Google Scholar]
- Li J, STOICA P, Xu L, et al. On Parameter Identifiability of MIMO Radar[J]. IEEE Signal Processing Letters, 2007, 14(12): 968–971 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Deng H, Geng Z, Himed B. MIMO Radar Waveform Design for Transmit Beamforming and Orthogonality[J]. IEEE Trans on Aerospace and Electronic Systems, 2016, 52(3): 1421–1433 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- XU J, Liao G, Zhu S, et al. Joint Range and Angle Estimation Using Mimo Radar with Frequency Diverse Array[J]. IEEE Trans on Signal Processing, 2015, 63(13): 3396–3410 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- LI J, Stoica P. MIMO Radar with Colocated Antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- BEKKERMAN I, Tabrikian J. Target Detection and Localization Using MIMO Radars and Sonars[J]. IEEE Trans on Signal Processing, 2006, 54(10): 3873–3883 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Friedlander B. On The Role of Waveform Diversity in MIMO Radar[C]//2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers, New York, NY, USA, 2011: 1501–1505 [Google Scholar]
- Qin S, Zhang Y D, Amin M G. DOA Estimation of Mixed Coherent and Uncorrelated Targets Exploiting Coprime MIMO Radar[J]. Digital Signal Processing, 2017, 61: 26–34 [Article] [CrossRef] [Google Scholar]
- Liu X, SUN C, Yang Y, et al. Hybrid Phase Shift and Shifted Sideband Beamforming for Large-Aperture Mimo Sonar Imaging[J]. IET Radar, Sonar & Navigation, 2017, 11(12): 1782–1789 [Article] [CrossRef] [Google Scholar]
- Xu L, Li J, STOICA P. Target Detection and Parameter Estimation for MIMO Radar Systems[J]. IEEE Trans on Aerospace & Electronic Systems, 2008, 44(3): 927–939 [Article] [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 MIMO声呐信号模型 |
| In the text | |
 |
图 2 MIMO阵列示意图 |
| In the text | |
 |
图 3 低信噪比下MIMO-TDS-MF的方位估计性能 |
| In the text | |
 |
图 4 存在发射阵列流形误差时的DOA估计性能 |
| In the text | |
 |
图 5 存在发射信号同步误差时的DOA估计性能 |
| In the text | |
 |
图 6 基于MVDR 3种估计方法运行100次的耗时曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


