Structural design and performance analysis of hopping robot with buffer devices

Jian WANG; Wenxiang ZHANG; Chenglong XU; Chenjie WANG

doi:10.1051/jnwpu/20254320316

All issues

Volume 43 / No 2 (April 2025)

JNWPU, 43 2 (2025) 316-325

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 2, April 2025


Page(s)		316 - 325
DOI		https://doi.org/10.1051/jnwpu/20254320316
Published online		04 June 2025

JNWPU 2025, 43(2): 316–325

Structural design and performance analysis of hopping robot with buffer devices

一种具有缓冲装置的跳跃机器人结构设计及性能分析

Jian WANG (王建), Wenxiang ZHANG (张文祥), Chenglong XU (许成龙) and Chenjie WANG (王晨杰)

School of Mechanical Engineering, Nanjing Institute of Technology, Nanjing 211167, China

Received: 12 April 2024

Abstract

The existing hopping robot has large landing impact and poor landing stability. Therefore, a hopping robot with a new buffer device is designed. The anti-rotation mechanism in the buffer device is used to reduce the landing impact. The unidirectional bearing and damping ring are jointly employed to avoid the rebound of the hopping robot when the buffer device absorbs ground impact forces. Based on the principles of robotic mechanism, the main structure of the hopping robot is designed. Its motion principles are analyzed and its motion procedures are developed. The kinematics models of the hopping robot in its takeoff, flight and landing stages are established by using the D-H method. Its dynamic models in the takeoff and flight stages are studied according to the second-type Lagrange method. Its landing stability is analyzed based on the zero moment point (ZMP) theory and the ZMP trajectory plot is drawn. The hopping robot prototype is developed with the 3D printing technique and experiments on it are carried out. The study results significantly enhance the hopping stability of the hopping robot and reduce its landing impact.

摘要

针对现有跳跃机器人落地冲击力大、落地不稳定的问题, 设计了一种具有新型缓冲装置的跳跃机器人, 拟利用缓冲装置中的止转机构减少落地冲击, 借助单向轴承与阻尼环的配合, 避免缓冲装置因吸收地面冲击力而造成机体回弹。根据机器人机构学原理, 设计了跳跃机器人的主体结构, 分析了其运动原理, 给出了弹跳流程图。采用D-H方法, 建立了跳跃机器人起跳、腾空、落地3个阶段的运动学模型, 使用第二类拉格朗日法, 建立了起跳和腾空阶段的动力学模型。基于零力矩点(ZMP)理论分析了跳跃机器人的落地稳定性, 计算并绘制了ZMP轨迹图。使用3D打印技术研制了跳跃机器人样机, 开展了试验测试研究。研究成果对提高机器人的跳跃稳定性、缓解落地冲击具有重要意义。

Key words: hopping robot / buffer device / structural design / kinematics / landing stability

关键字 : 跳跃机器人 / 缓冲装置 / 结构设计 / 运动学 / 落地稳定性

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

跳跃机器人在高速运动中与地面接触, 在地面冲击力的作用下完成着陆过程。冲击力的大小与跳跃机器人的飞行姿态、足部质量和支承面积、落地瞬间的着地速度、有无缓冲装置等息息相关[1]。地面冲击力过大, 不仅会影响机器人的跳跃性能, 还会造成机载设备损坏或机器人侧翻。相关研究表明, 良好的着陆缓冲装置是保证跳跃机器人具有优良弹跳性能的重要因素之一[2]。

对于跳跃机器人着陆缓冲机构的研究大多基于新材料、新结构(如刚柔混合结构、变结构的复合仿生结构等)展开的。Kovac等[3]研制了一种具有碳纤维外框架的跳跃机器人, 在落地时外框架能够很好地吸收地面冲击力, 进而减少落地冲击。Armour与Ho等[4–5]研制的跳跃机器人均是采用外框架进行着陆缓冲。Wood和Birkmeyer等[6–7]研制了一种多足机器人, 该机器人的腿由刚性连杆和高分子聚合物铰接而成, 可以实现柔性缓冲。Galloway等[8]研制了一种多足机器人, 该机器人腿部刚度可调, 可实现一定程度的缓冲。为减少跳跃机器人地面支撑力、腿部弹簧力和腿部连杆抗冲击能力的差异, 陈殿生等[9]以仿生蝗虫跳跃机器人为研究对象, 提出了一种能量分配原则, 可有效减缓落地冲击。肖竟成[10]利用扭簧、旋转阻尼器和凸轮随动器的配合, 研制出一种缓冲机构, 能够缓解落地冲击, 减少落地回弹, 提高落地稳定性。文献[11–14]均是以仿袋鼠跳跃机器人为研究对象, 分析证明了柔性关节或柔性脚能够吸收部分地面冲击力, 具有较好的落地缓冲效果。上述研究对于减缓落地冲击、提高机器人能量使用效率具有重要意义, 但是对于缓冲方式的研究还不够深入。鉴于此, 本文建立了一种具有新型缓冲装置的跳跃机器人, 拟利用止转机构减少落地冲击, 利用单向轴承与阻尼环的配合, 缓慢释放弹性元件的弹性势能, 避免缓冲装置因吸收地面冲击力而造成机体回弹。

1 机构组成及运动原理

1.1 整体结构

图 1a)为跳跃机器人整体结构模型, 主要由支撑壳体、传动机构、弹跳腿和足部缓冲装置四部分组成。支撑壳体用来连接弹跳腿，安装驱动电机、传感器、传动轴等零部件; 传动机构用来实现运动和动力的传递; 弹跳腿主要起到支撑作用, 用来实现机器人的站立和跳跃; 足部缓冲装置主要由止转机构和变阻尼机构组成, 用来减少落地冲击。

在图 1b)中, 驱动电机与主动齿轮相连, 从动齿轮、中部输入齿轮和过渡输入齿轮安装在输入齿轮轴上, 过渡输出齿轮、左输入齿轮和右输入齿轮安装在过渡轴上, 中部输出齿轮安装在腿轴上, 左输出齿轮和右输出齿轮分别安装在左空心轴和右空心轴上。左、右空心轴均为中空结构, 放置在腿轴的两侧, 且在中空位置安装有轴承(右空心轴承未标出)。机器人的第一大腿和第二大腿分别固定在腿轴与空心轴上。其运动原理是: 驱动电机通过主动齿轮带动输入齿轮轴转动, 通过中部输入齿轮和中部输出齿轮的啮合, 带动腿轴正向旋转; 在过渡输入齿轮和过渡输出齿轮的啮合作用下, 过渡轴带动左、右输入齿轮转动, 通过左输入齿轮与左输出齿轮的啮合、右输入齿轮与右输出齿轮的啮合, 带动空心轴反向转动。在转向相反的腿轴和空心轴的共同驱动菱形四杆机构做同步反向运动, 其优点是不仅减少了电机数量, 还可以提高运动的同步性和可控性。

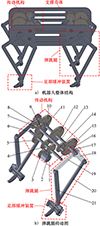图1

跳跃机器人整体结构模型

1.2 缓冲机理

现有的缓冲装置在吸收地面冲击力之后, 大都会迅速释放弹性元件的弹性势能, 造成机体回弹。本文设计了一种变阻尼缓冲机构, 单向轴承和阻尼环的配合能够缓慢释放弹性元件的弹性势能, 避免机器人落地回弹, 可有效提高其落地稳定性。如图 2所示, 阻尼环安装在能够顺、逆时针旋转的足部轴上, 只能够顺时针旋转的单向轴承安装在缓冲架的轴承孔内。当机器人与地面接触瞬间, 足部轴、阻尼环以及单向轴承均顺时针旋转, 弹性元件快速吸收地面冲击力。吸收完冲击力之后, 弹性元件开始释放弹性势能, 带动足部轴与阻尼环逆时针旋转。由于单向轴承无法逆时针旋转, 会产生较大阻尼, 在该阻尼的作用下, 弹性元件会缓慢释放弹性势能, 可避免发生因弹性势能瞬间释放造成机体回弹的现象。

依据上述缓冲原理, 设计出的足部缓冲装置如图 3所示。其基本原理为: 在机器人姿态调整时, 伸缩电机启动, 推杆推动挡板、挡板推动止转销向内缩进, 直至止转销圆头侧与缓冲架接触; 在机器人起跳时, 挡板会阻挡止转销沿滑槽向上运动, 由于扭簧无法扭转, 缓冲装置失去缓冲功能。在机器人落地瞬间, 伸缩电机启动, 推杆推动挡板、挡板推动止转销向外伸出, 止转销沿滑槽向上运动, 并且在滑体的作用下向外伸出, 此时单向轴承正向旋转, 阻尼环也正向旋转。单向轴承与阻尼环的配合相当于旋转轴承, 不会对扭簧吸收地面冲击力造成影响。当缓冲装置吸收完冲击力之后, 由于单向轴承不能反向旋转, 阻尼环反向旋转的阻力将会增大, 在单向轴承与阻尼环的配合下, 存储在扭簧中的弹性势能会缓慢释放, 最终止转销穿过挡板恢复到最初的位置, 为下一次缓冲做准备。

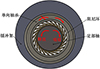图2

缓冲原理图

图3

缓冲装置图

1.3 弹跳运动流程

跳跃机器人的弹跳运动流程如图 4所示。跳跃机器人首先调节起跳姿态和起跳角度, 之后伸缩电机启动, 在伸缩电机的作用下, 止转销向内压入, 缓冲装置失去缓冲功能。驱动电机正转带动齿轮旋转, 动力经过传动机构传递到弹跳腿上, 使弹跳腿快速下压, 机体迅速上升, 机器人完成起跳。机器人准备落地时, 驱动电机反向旋转至第一、第二大腿呈直线位置, 伸缩电机伸长将止转销向外抽出, 缓冲装置启动。机器人落地瞬间, 缓冲装置吸收冲击力, 在单向轴承和阻尼环的配合作用下, 扭簧缓慢释放由冲击力产生的弹性势能, 当止转销运动到导滑槽底部时, 弹性势能释放完毕, 重复上述流程可以实现机器人的连续跳跃。

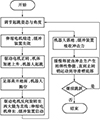图4

弹跳运动流程图

2 运动学分析

2.1 起跳阶段的运动学

2.1.1 运动学模型的建立

跳跃机器人为两侧对称结构, 本文取单侧模型开展研究。跳跃机器人简化后的单侧模型如图 5所示, 弹跳腿菱形四杆DECB和D′E′C′B′分别化简成杆BE和B′E′, 机器人躯干用虚线EE′表示, 其中杆BC和杆BD的长度为a, 杆EC和杆ED的长度为b, 前肢与后肢对应相等, 各杆件间夹角关系见图 5。

由图 5中的几何关系可知, BE的长度为

跳跃机器人四肢结构相同且运动状态一致, 因此本文取前肢进行分析。假设机器人起跳时足部与地面不发生分离与滑动, 取O₀点为原点建立固定坐标系O₀-x₀y₀z₀, 取杆的方向为x轴方向建立各动坐标系, 其中z轴方向垂直纸面朝外, 见图 6。假设θ_i表示机器人各关节转角, l_i为杆长, 根据D-H法, 机器人着地阶段的参数见表 1。

运用D-H法可得, 相邻杆件的位姿变换矩阵为

式中, i=1, 2, 3, 4。

从固定坐标系O₀-x₀y₀z₀开始, 将各杆件的局部坐标系变化矩阵按照顺序依次连乘, 即可得到各杆件坐标系相对于固定坐标系O₀-x₀y₀z₀的位置。膝关节O₂、髋关节O₃、躯干O₄相对于固定坐标系O₀-x₀y₀z₀的位置_i⁰P可表示为

式中，为书写方便, cosθ₁和sinθ₁分别简写为C₁和S₁, cos(θ₁+θ₂) 简写为C₁₊₂, sin(θ₁+θ₂)简写为S₁₊₂, 以此类推。

跳跃机器人的逆运动学是通过杆件位姿计算关节转位角的变化情况。采用坐标函数变换矩阵逆向乘法的变换方法, 可得

式中, A, B, C分别为

式中: p_x, p_y, p_z分别表示机器人质心在参考坐标系中的坐标; n_x, n_y, n_z分别为对应关节所处坐标系的x轴方向的单位向量在固定坐标系O₀-x₀y₀z₀中的坐标。

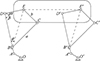图5

机器人简化模型

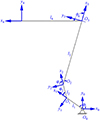图6

起跳阶段坐标系

表1

起跳阶段机器人参数

2.1.2 运动步态分析

根据表 1及(1)~(6)式, 利用MATLAB软件可以画出机器人起跳过程中各杆件的位姿图, 见图 7。

由图 7可知, 整个起跳阶段4杆弹跳腿处于一个拉长的状态。以弹跳腿第一和第二大腿形成一条直线为分界点, 机器人步态图分为2个阶段：第一阶段是第一和第二大腿未成一条直线之前的姿态变化(蓝色线)；第二阶段是第一和第二大腿形成一条直线之后的姿态变化(红色线)。在第一阶段, 弹跳腿后撤, 大腿杆件拉长, 躯干抬升, 在第二阶段弹跳腿变为前倾, 大腿杆件迅速拉长, 机体迅速上升, 完成起跳。

图7

机器人起跳阶段运动步态图

2.2 腾空阶段的运动学

机器人腾空阶段的运动是在重力场下的抛物线运动。图 8是机器人在腾空阶段的关节坐标系, 各杆件长度与旋转角度变化范围如表 2所示。

采用与起跳阶段相同的计算方法, 可获得跳跃机器人在腾空阶段的运动步态图, 如图 9所示。由图 9可知, 机器人在腾空阶段躯干保持不动, 弹跳腿的大腿向上收缩, 足部与小腿向上抬升并且向前伸展, 为后续落地缓冲做出姿态调整。

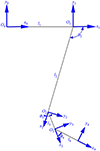图8

腾空阶段坐标系

表2

腾空阶段机器人参数

图9

机器人腾空阶段运动步态图

2.3 落地阶段的运动学

机器人落地阶段与起跳阶段的坐标系类似, 不作重复绘制。机器人落地阶段各杆件长度与旋转角度变化范围如表 3所示。

采用同样的方法, 可以获得跳跃机器人在腾空阶段的运动步态图, 如图 10所示。由图 10可知, 弹跳腿在落地过程中, 踝关节的角度变化较大, 而弹跳腿的大腿部分以及躯干部分在整个落地过程中摆幅很小, 说明缓冲机构具有很好的缓冲效果与落地稳定性。

表3

落地阶段机器人参数

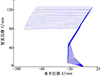图10

机器人落地阶段运动步态图

3 动力学和落地稳定性分析

为了研究机器人跳跃过程的动态特性, 本节在运动学的基础上对机器人起跳、落地2个阶段进行动力学分析, 以获得2个阶段的机器人关节力矩, 之后采用ZMP理论对机器人落地稳定性进行分析。

3.1 动力学分析

本文采用第二类拉格朗日平衡法, 从能量角度计算机器人关节力矩。第二类拉格朗日方程为

式中：T和V分别表示系统的总动能和总势能；θ_i是各关节角坐标；τ_i是各关节力矩。

3.1.1 起跳阶段动力学分析

假设机器人起跳阶段足底与地面不发生滑动, 机器人的总动能由杆件平动和转动的动能组成, 起跳阶段机器人的总动能可表示为

式中: m_i为各杆件的质量；v_xi和v_yi分别表示各杆件水平和竖直方向的速度分量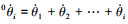；, J_i是各杆件的转动惯量, J_i=m_il_i²/12。

总势能V可表示为

式中，h_ci为各杆件质心的位置高度。

将(8)~(9)式代入(7)式可得到起跳阶段的关节力矩表达式为

将各关节杆件长度、位置等参数代入相应关节力矩表达式中, 可计算得到起跳阶段踝关节、膝关节和髋关节的力矩。由计算数据可知, 踝关节在起跳时力矩为0, 这是因为起跳阶段止转销被挡板阻挡, 踝关节不能转动, 仅起到固定连接的作用。3个关节中, 膝关节所需力矩最大(约为112 N·mm), 主要是因为在质量一定的前提下, 踝关节固定不动, 膝关节承受的惯性力会增加。

3.1.2 落地阶段动力学分析

机器人落地时缓冲装置开始工作, 扭簧发生转动, 具有弹性势能。因此, 落地阶段的势能由机器人产生的重力势能和扭簧产生的弹性势能组成

式中：V_g和V_s分别表示重力势能和弹性势能；k是扭簧的刚度系数；θ₂₀是扭簧初始相对转角。

落地阶段各杆件的运动与起跳阶段类似, 其总动能扔按(8)式进行计算。将(8)式和(11)式代入(7)式中, 使用Matlab可计算得到落地阶段机器人各关节扭矩。由计算结果可知, 在0~0.016 s时间段, 足部刚开始接触地面, 各关节力矩迅速上升, 膝关节力矩最大, 峰值约为72.2 N·mm, 踝关节力矩最小, 峰值约为39.4 N·mm; 在0.016~0.03 s时间段, 各关节力矩迅速下降, 说明柔性关节具有良好的缓冲作用; 在0.03~0.21 s时间段, 力矩变化平缓。

3.2 落地稳定性分析

落地稳定性是衡量跳跃机器人动态特性的重要指标, 其研究方法大都采用Vukobratovic提出的零力矩点(ZMP)理论。本文也采用该方法对新型跳跃机器人的落地稳定性进行分析。

3.2.1 稳态裕度

稳态裕度d_ZMP是衡量落地稳定性的主要指标, 其定义是ZMP点到中心位置的距离, d_ZMP数值越小, ZMP点距离中心位置越近, 机器人就越稳定, 反之越不稳定[15]。

稳态裕度可以表示为

式中, X_ZMP为ZMP点的横坐标。

3.2.2 ZMP的计算分析

由文献[15]可知, X_ZMP的轨迹可表示为

式中: x_i和y_i与分别是各杆件在落地阶段质心横坐标与纵坐标; τ_i是各类节力矩。

根据(13)式, 利用MATLAB软件可得到机器人落地阶段X_ZMP轨迹图, 如图 11所示。由图 11可知:

1) 机器人足部刚接触地面时, ZMP点位于足部前侧(图 11中心位置上方); 在0.08 s之后, 足部处于稳定状态, ZMP点变化趋于平稳, 并向中心位置靠近; 在0.17 s经过中心位置, ZMP点向足部后侧变化(图 11中心位置下方), 随后向中心位置靠近。

2) 整体来看, X_ZMP轨迹曲线均在稳定区域内, 且未发生突变, 说明机器人落地阶段具有良好的稳定性。

图11

落地阶段X_ZMP轨迹

4 样机试制与试验测试

为了验证结构设计的合理性和理论分析的准确性, 利用3D打印技术制作了机器人样机, 搭建了试验测试平台, 开展了跳跃能力实验、起跳稳定性实验、落地缓冲对比实验。为了使结构轻量化, 弹跳腿的厚度取4.5 mm, 宽度为10 mm, 缓冲架与足部的厚度为5 mm。传动机构中空心轴选用内径为12 mm、外径为14 mm, 长度为35 mm的6061空心圆铝管。足部轴选用直径为5 mm, 长度为50 mm的6061铝棒, 止转销选用直径为2.6 mm的空心针, 并截取长度50 mm, 扭簧线径为1.2 mm, 外径为9 mm, 轴承型号为AXK2035。因四肢弹跳腿与缓冲装置在落地时受到的冲击力比较大, 选择抗冲击能力强、强度高, 密度为1.02 g/cm³的ABS材料, 壳体与传动机构选择价格比较低廉、硬度比较高, 密度为1.3 g/cm³的普通光敏树脂进行3D打印。装配好的跳跃机器人整机尺寸为260 mm×130 mm×180 mm。

4.1 跳跃能力试验

试验采用的驱动电机为4008-150T云台无刷电机, 控制器为Deng-ge FOC控制器, 传感器选用量程为0.02~20 kg的薄膜压力传感器、VL53L0X激光测距传感器和MPU6050六轴-角度加速度传感器。按照图 4所示的弹跳运动流程, 起跳开始前调整起跳姿态，然后跳跃机器人开始起跳, 图 12为实验测试视频截图。图 13~14分别为机器人跳跃的水平位移和竖直位移曲线图。

由图 13可知, 在0~0.06 s时间段, 机器人水平位移变化缓慢, 在0.06~0.365 s时间段, 水平位移快速增加, 并达到最大值, 约为76 mm。由于在下落过程中, 机器人前肢先着地使其前倾, 接着后肢再着地, 这就造成0.365 s之后水平位移有下滑的现象。由图 14可知, 在0~0.21 s时间段, 机器人竖直高度迅速增长并达到最大高度173 mm, 在0.21~0.365 s时间段, 机器人处于下落阶段, 竖直高度持续下降, 并在0.365 s接触地面。

图 15~16分别是机器人水平速度与竖直速度的曲线变化图, 由图可知: 在0.06 s时, 水平速度与竖直速度达到最大值, 此时机器人离开地面, 在0.21 s竖直速度变为0 mm/s, 此时机器人开始降落, 直至0.365 s竖直速度达到最大值1 490 mm/s, 此时水平速度也降为0 mm/s, 在0.55 s时机器人竖直速度变为0 mm/s。

试验测试视频截图

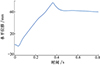机器人弹跳的水平位移

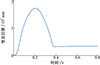机器人弹跳的竖直位移

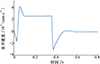机器人弹跳的水平速度

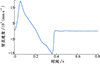机器人弹跳的竖直速度

4.2 落地缓冲对比试验

落地缓冲对比试验主要是为了研究缓冲装置对冲击力的影响。由于机器人落地时四肢足底与地面接触的时刻会有误差, 本文测量时选取每组数据的平均值作为测量结果。由测试结果可知, 无落地缓冲装置时, 地面的瞬时冲击力约为290 N, 而有落地缓冲装置时, 地面的瞬时冲击力约为72 N, 减少了75.2%。由此可见, 本文设计的缓冲装置能够有效减少机器人的瞬时冲击力, 起到保护机器人零部件和机载装置的作用。

5 结论

1) 建立了具有缓冲装置的跳跃机器人结构模型。设计了跳跃机器人整体方案, 建立了支撑壳体、传动机构、弹跳腿和足部缓冲装置的结构模型, 分析了其缓冲机理, 给出了其弹跳运动流程。

2) 分析了跳跃机器人的运动特性。采用D-H方法, 建立了跳跃机器人起跳、腾空、落地3个阶段的运动学模型, 得出了其运动位姿图。采用拉格朗日法, 建立了机器人起跳和腾空阶段的动力学模型, 获得了其关节力矩, 基于ZMP理论, 分析了跳跃机器人的落地稳定性, 计算并绘制了ZMP轨迹图, 研究表明该机器人具有良好的落地稳定性。

3) 研制了机器人样机, 开展了试验测试研究。利用3D打印技术, 制作了物理样机, 完成了跳跃能力试验和落地缓冲对比试验。测试结果表明: 机器人可以实现稳定跳跃, 且有缓冲装置时的地面冲击力比无缓冲装置时减少了约75.2%。

References

LIU Zhuangzhi, ZHU Jianying, WU Hongtao, et al. Analysis on the landing impact and stability of the intermittent one-legged hopping robots[J]. Mechanical Science and Technology for Aerospace Engineering, 2004, 23(9): 1068–1071 (in Chinese) [Google Scholar]
MO Xiaojuan, GE Wenjie, ZHAO Donglai, et al. Review: research status of miniature jumping robot[J]. Journal of Mechanical Engineering, 2019, 55(15): 109–123 (in Chinese) [Google Scholar]
KOVAC M, SCHLEGEL M, ZUFFEREY JC, et al. A miniature jumping robot with self-recovery capabilities[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009: 583–588 [Google Scholar]
ARMOUR R, PASKINS K, BOWYER A, et al. Jumping robots: a biomimetic solution to locomotion across rough terrain[J]. Bioinspiration & Biomimetics, 2007, 2(3): 65–82 [Google Scholar]
HO T, LEE S. A novel design of a robot that can jump and roll with a single actuator[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 2012: 908–913 [Google Scholar]
WOOD R J, AVADHANULA S, SAHAI R, et al. Microrobot design using fiber reinforced composites[J]. Journal of Mechanical Design, 2008, 130(5): 052304. [Article] [Google Scholar]
BIRKMEYER P, PETERSON K, FEARING R S. DASH: a dynamic 16g hexapedal robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009: 2683–2689 [Google Scholar]
GALLOWAY K C, CLARK J E, KODITSCHEK D E. Design of a tunable stiffness composite leg for dynamic locomotion[C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, California, USA, 2009: 1–8 [Google Scholar]
CHEN Diansheng, ZHANG Ziqiang, CHEN Kewei. Energy allocation in landing buffering process for biomimetic locust mechanism[J]. Chinese Journal of Mechanical Engineering, 2015, 51(13): 196–202 (in Chinese) [Google Scholar]
XIAO Jingcheng. Design and analysis of the structure of the buffer device of the bionic frog forelimb movement law[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]
GAO Lixia, DONG Haijun, GE Wenjie, et al. Analysis of the landing impact of a hopping kangaroo robot taking its flexible toes into consideration[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10): 1688–1692 (in Chinese) [Google Scholar]
CHENG Jing, GE Wenjie, WEI Dunwen, et al. Research on motion features of kangaroo hopping robot's flexible curve foot based on beam with varying section in the stance stage[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(12): 1898–1903 (in Chinese) [Google Scholar]
CHEN Pengwei, GE Wenjie, DONG Haijun. Research on landing stability of hopping robot considering flexible joint[J]. Journal of Machine Design, 2013, 30(1): 35–39 (in Chinese) [Google Scholar]
LI Yan, GE Wenjie, KOU Xin. Research and design on foot of hopping kangaroo robot based on compliant mechanisms[J]. Journal of Machine Design, 2013, 30(2): 18–24 (in Chinese) [Google Scholar]
CHENG Wei. Leg structure optimization and landing stability analysis of grasshopper bionic robot[D]. Zhuzhou: Hunan University of Technology, 2021 (in Chinese) [Google Scholar]

All Tables

起跳阶段机器人参数

腾空阶段机器人参数

落地阶段机器人参数

All Figures

	图1 跳跃机器人整体结构模型
In the text

	图2 缓冲原理图
In the text

	图3 缓冲装置图
In the text

	图4 弹跳运动流程图
In the text

	图5 机器人简化模型
In the text

	图6 起跳阶段坐标系
In the text

	图7 机器人起跳阶段运动步态图
In the text

	图8 腾空阶段坐标系
In the text

	图9 机器人腾空阶段运动步态图
In the text

	图10 机器人落地阶段运动步态图
In the text

	图11 落地阶段X_ZMP轨迹
In the text

	图12 试验测试视频截图
In the text

	图13 机器人弹跳的水平位移
In the text

	图14 机器人弹跳的竖直位移
In the text

	图15 机器人弹跳的水平速度
In the text

	图16 机器人弹跳的竖直速度
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] LIU Zhuangzhi, ZHU Jianying, WU Hongtao, et al. Analysis on the landing impact and stability of the intermittent one-legged hopping robots[J]. Mechanical Science and Technology for Aerospace Engineering, 2004, 23(9): 1068–1071 (in Chinese) [Google Scholar]

[2] MO Xiaojuan, GE Wenjie, ZHAO Donglai, et al. Review: research status of miniature jumping robot[J]. Journal of Mechanical Engineering, 2019, 55(15): 109–123 (in Chinese) [Google Scholar]

[3] KOVAC M, SCHLEGEL M, ZUFFEREY JC, et al. A miniature jumping robot with self-recovery capabilities[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009: 583–588 [Google Scholar]

[4] ARMOUR R, PASKINS K, BOWYER A, et al. Jumping robots: a biomimetic solution to locomotion across rough terrain[J]. Bioinspiration & Biomimetics, 2007, 2(3): 65–82 [Google Scholar]

[5] HO T, LEE S. A novel design of a robot that can jump and roll with a single actuator[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 2012: 908–913 [Google Scholar]

[6] WOOD R J, AVADHANULA S, SAHAI R, et al. Microrobot design using fiber reinforced composites[J]. Journal of Mechanical Design, 2008, 130(5): 052304. [Article] [Google Scholar]

[7] BIRKMEYER P, PETERSON K, FEARING R S. DASH: a dynamic 16g hexapedal robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009: 2683–2689 [Google Scholar]

[8] GALLOWAY K C, CLARK J E, KODITSCHEK D E. Design of a tunable stiffness composite leg for dynamic locomotion[C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, California, USA, 2009: 1–8 [Google Scholar]

[9] CHEN Diansheng, ZHANG Ziqiang, CHEN Kewei. Energy allocation in landing buffering process for biomimetic locust mechanism[J]. Chinese Journal of Mechanical Engineering, 2015, 51(13): 196–202 (in Chinese) [Google Scholar]

[10] XIAO Jingcheng. Design and analysis of the structure of the buffer device of the bionic frog forelimb movement law[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]

[11] GAO Lixia, DONG Haijun, GE Wenjie, et al. Analysis of the landing impact of a hopping kangaroo robot taking its flexible toes into consideration[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10): 1688–1692 (in Chinese) [Google Scholar]

[12] CHENG Jing, GE Wenjie, WEI Dunwen, et al. Research on motion features of kangaroo hopping robot's flexible curve foot based on beam with varying section in the stance stage[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(12): 1898–1903 (in Chinese) [Google Scholar]

[13] CHEN Pengwei, GE Wenjie, DONG Haijun. Research on landing stability of hopping robot considering flexible joint[J]. Journal of Machine Design, 2013, 30(1): 35–39 (in Chinese) [Google Scholar]

[14] LI Yan, GE Wenjie, KOU Xin. Research and design on foot of hopping kangaroo robot based on compliant mechanisms[J]. Journal of Machine Design, 2013, 30(2): 18–24 (in Chinese) [Google Scholar]

[15] CHENG Wei. Leg structure optimization and landing stability analysis of grasshopper bionic robot[D]. Zhuzhou: Hunan University of Technology, 2021 (in Chinese) [Google Scholar]