| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 983 - 991 | |
| DOI | https://doi.org/10.1051/jnwpu/20193750983 | |
| Published online | 14 January 2020 | |
Optimization Study of High Altitude Micro Gliding Air Vehicle Re-Entry Path Characteristics
高空微型飞行器滑翔轨迹特性优化研究
Academy of Opto-Electronics, Chinese Academy of Science, Beijing 100190, China
Received:
12
October
2018
Based on the characteristics of the configuration and flight of the micro gliding air vehicle (MGAV), an analysis and optimization for general gliding path of different mission demands is carried out. Firstly, an overall design method and parameters are summarized. Secondly, the equilibrium glide launching parameters are determined based on the general aircraft re-entry equation. The real launching parameter are also developed by considering the real launching facility. Furthermore, the un-controlled maximum-range-towards path characteristics for the real and equilibrium glide are compared and analyzed. The range in equilibrium glide is 5 km larger than real glide. Then, two potential flight demand are explained and the Gauss pseudo-spectral method is adopted to solve the maximum endurance and the maximum endurance and range with the process constraint and final constraint. The first target is 8 minutes longer than the original glide path but the range is 20 km less compared to the maximum range. The second target could keep the maximum range and at the meantime, the endurance could be increased 2 minutes. Finally, the control variables are substituted into the dynamic equations to validate the results. The result shows that the Gauss pseudo-spectral method is an effective and feasible way to solve the optimum gliding path.
摘要
基于滑翔式微型飞行器(micro gliding air vehicle,MGAV)的布局、投射及飞行特点,分析并优化其在不同任务需求下的一般轨迹特性。首先,概述了此种MGAV的设计过程及总体参数;接着,基于一般意义的飞行器平面运动模型,推导出平衡滑翔初始投射条件,并结合实际投射装置参数推导真实初始投射条件。进一步分别比较了在这两种投射条件下的无约束最远射程轨迹特性,真实滑翔比平衡滑翔在射程上减少约5 km。然后,分析了此种飞行器可能存在的任务需求,采用高斯伪谱法得到在过程约束及终端约束下最长滑翔时间及保证滑翔时间及滑翔距离同时最长2种目标函数下的最优滑翔轨迹。第一种目标下,优化后航时和无控滑翔相比可提高约8 min,但是和理论最远射程136 km相比缩短20 km。第二种目标下,在最远射程维持不变的同时可使航时提高约2 min。最后,将优化轨迹的控制变量带入到动力学方程积分进行可行性验证。研究结果表明,基于高斯伪谱法的轨迹分析是一种高效可行的轨迹优化策略。
Key words: micro gliding air vehicle / gliding path characteristics / Gauss pseudo-spectral method / low Reynolds number / flat plate airfoil
关键字 : 滑翔式微型飞行器 / 轨迹特性 / 高斯伪谱法 / 低雷诺数 / 平板翼型
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
微型飞行器在军民用领域都具有极大的潜力和价值[1-1]。20世纪90年代以来, 由于灵活多样用途特殊, 微型飞行器备受关注, 其技术研究已取得了较大进步[3-3], 但受限于微机电技术的发展水平, 目前, 航时和航程不足已成为制约微型飞行器性能发挥的瓶颈之一。
常规的微型飞行器依靠微型电机进行有动力飞行, 但是有限的能源使其难以有效续航。美国海军实验室(Naval Research Laboratory, United States)于2012年提出一种微型飞行器的新式应用方法, 并将其命名为CICADA(close-in covert autonomous disposable aircraft)。区别于传统微型飞行器的动力飞行方式, CICADA去掉了动力装置, 仅携带基本控制元件和任务传感器。其原理样机被挂于Tempest无人机的机翼下方, 由高空气球作为载具将Tempest无人机携带到2万米高空进行释放。飞行一段时间后, CICADA脱离Tempest无人机, 全程依靠滑翔的方式完成到预定地点的精确着陆[5]。CICADA成本较低, 结构简单, 一次可从平流层大量投放, 具有执行多种特定任务的能力。其原理样机已经经过多次优化及测试[6]。事实上, 国内外平流层投放飞行器的研究越来越受到重视。如德国宇航中心于瑞典基律纳发放场进行的平流层常规布局滑翔机投放验证了平流层投放技术的可行性及控制算法的精确性[7]。但是现有的研究大多面向常规布局中大型尺寸滑翔飞行器, 而对平流层投放的微型飞行器缺乏系统性研究。
目前, 轨迹优化分析是滑翔飞行器研究的重要方面, 文献研究多针对大质量高速飞行器, 如导弹、返回舱或航天飞机[8-8]等。而对于平流层投放的微型滑翔飞行器来说, 由于其概念较为新颖, 目前其滑翔轨迹优化方面的系统性研究还有待深入。
本文参照常规航天飞行器再入方程, 概述了微型滑翔飞行器(MGAV)的设计过程。基于微型滑翔飞行器总体设计要求及参数, 分析其一般意义下的平衡滑翔和真实滑翔轨迹特性。并针对潜在的目标需求, 应用高斯伪谱法对运动方程进行离散处理, 完成对2种可能的任务需求的最优轨迹设计。最后针对最优控制变量进行反解验证了高斯伪谱法对于最优轨迹求解的可行性和高效性。
1 MGAV设计概述
1.1 总体设计思路与设计过程
滑翔式微型飞行器的最终目标是携带载荷完成由高空到预定地点的精确着陆。其设计需要在完成任务的同时, 具有较好的隐蔽性, 因此对飞行器尺寸进行了约束。并且, 由于该飞行器不再回收, 在设计时还需要考虑到成本低廉及结构简单等因素。为此, 该飞行器展长被限制在35 cm之内以增强隐蔽性。并且, 为了增大翼载荷以降低滑翔时的速度, 该飞行器采用飞翼布局, 翼面积为0.04 m2, 展弦比在2以内。
根据上述设计思路, 决定直接以电路板作为机翼以达到降低成本和快速批量制造的目的。根据文献[13]的证明, 飞行器在以最大升阻比滑翔时可以达到最远滑翔距离。根据这一结论, 在翼面积及展弦比约束下设计可以使飞行器达到最佳升阻比的翼面形状。由于使用电路板制作机翼, 飞行器将采用典型的薄翼平板翼型。整个下滑过程中, 飞行雷诺数较低。文献[14-17]通过实验详细研究了有限展弦比不同翼面形状的平板翼型机翼在低雷诺数下的气动性能, 见表 1。
平板翼型不同翼面形状气动参数
 |
图 1 平板翼型不同翼面形状气动参数 |
1.2 气动外形与参数估算
对于有限展长平板翼型机翼的升力系数, 可采用Plohamus[21]公式, 其表述如下
式中, Kp根据不同的气动布局有特定的取值。文献[14]根据实验数据给出针对展弦比为2的反齐默曼形状Kp取值为2.65;Kv=π; α为飞行器攻角。
对于阻力系数的预测, 可应用如下经典公式[15]
式中, CD0在这里取值为0.015;K为诱导阻力系数, 其根据不同气动布局取值不同[14]。这里K对于所述布局取值为0.355。表 2总结了此版自主设计MGAV总体参数。
微型滑翔式无人机总体参数
2 轨迹分析方法
2.1 运动方程
在运动分析过程中, 为了得到一般意义下的下滑轨迹和参数, 在这里不考虑滑翔过程中突风的影响。并且, 做出如下应用通常意义下的假设:①假设地球为均匀球体且由于再入时间较短, 忽略自转。②飞行器控制系统设计良好, 即再入段为平面运动。③飞行器绕质心运动为瞬时平衡, 即忽略绕质心的运动。基于以上假设并参考再入方程[18], 给出微型滑翔飞行器质心的平面运动方程和坐标系
式中,V表示飞行器速度, θ表示速度倾角(下滑角), r表示飞行器质心到地心的距离, R表示射程(滑翔距离), H表示飞行器质心到地面的垂直距离。Re, m和g分别表示地球半径、飞行器质量和当地重力加速度。L=0.5ρV2SCL, D=0.5ρV2SCD分别表示飞行器升力和阻力。其中, CL和CD表示飞行器的升力和阻力系数, 其为攻角的函数。ρ和S分别表示当地大气密度和飞行器的参考面积。坐标系如图 2所示。
对于大气密度, 这里采用根据国际标准大气简表数值拟合而成的公式得到和高度的关系
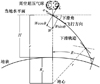 |
图 2 平面再入坐标系变量关系 |
2.2 平衡滑翔投射条件
对于滑翔式微型飞行器来说, 其最理想的滑翔轨迹是无波动的平稳下滑飞行, 即平衡滑翔。假设微型飞行器从弹射器脱离时刻开始即进入到稳定的下滑轨道, 这对于一个已经确定设计参数的飞行器, 一定存在一种初始条件使其在不同高度可以在全程保持平衡滑翔状态, 其推导过程如下:
由平衡滑翔定义可知, 当飞行器平衡滑翔时, 升力与重力相等或极为接近。由此可近似下滑角θ为一可忽略小量, (3)式中第二式dθ/dt≈0, cosθ≈1。因此(3)式第二式可改写为
通过(5)式可求出平衡滑翔时初始时刻需要的速度Vinitial。(5)式对ρ求导可得
对(3)式第一式左边项进行改造可得
对(7)式dρ/dt进行改造可得
dρ/dH的函数关系可由密度高度关系拟合公式(4)给出, 将其带入(8)式并将(6)式与(8)式代入公式(7)可得
在高度、密度和初始速度已知的情况下则可通过(9)式求解出平衡滑翔条件下的初始速度倾角。由公式(5)与(9)计算得到在MGAV设计高度20 km下平衡滑翔条件为:Vinitial=74.62 m/s, θinitial=-3.97°。而对于地面弹射, 此速度仅需约18 m/s。
2.3 实际滑翔投射条件
在此版设计中, 滑翔式微型飞行器采用由高空气球所携带的弹射装置在高空对其进行发放。弹射装置主要由导轨、滑块及弹簧组成。飞行器和滑轮一体, 在发放前滑轮放于导轨顶部压缩弹簧, 飞行器整体由挡板卡住固定。发放时上部挡板打开, 飞行器由弹簧推动沿滑轨下冲, 脱离滑轨后进入滑翔状态。弹射装置及飞行器发放前的受力状态可以简化成图 3形式。其中, 导轨全长为L, 导轨与当地水平线夹角为θ, 滑块与导轨的摩擦因数为μ。Fe, Fd, Fn分别为弹簧力、摩擦力和支撑力。
推导滑块的运动方程以估算其脱离速度, 由于垂直于导轨方向的力始终平衡, 所以只需列出平行于导轨方向的运动学方程, 其形式如下
式中,k为弹簧刚度。方程(10)属于二阶非齐次常微分方程, 带入初始条件:x(0)=0, ẋ(0)=0则可以求出其理论解为
对于真实应用于此种微型飞行器投射的装置参数, 导轨全长L=0.6 m, k=200 N/m, m=200 g, θinitial=40°, μ=0.1。图 4给出了飞行器经过滑轨加速的滑翔初始速度。经过0.05 s后飞行器速度被加速到约18 m/s脱离滑轨进入滑翔状态。
由上述对真实投射装置的分析可以看到, 弹射器的加速能力只能保证无人机在地面的平衡滑翔条件, 而20 km高空时离上述平衡滑翔初速度仍相距较大。但考虑到滑轨将无人机在上升时全程约束在一固定姿态, 可保证无人机投射时姿态的稳定, 因此在这一版设计中仍然保留弹射机构。图 5分别给出了由四阶Runge-Kutta法求解的最大升阻比下平衡滑翔条件和真实投射条件的无约束运动状态。
满足平衡滑翔投射条件, 整个运动轨迹在全程下滑平缓, 而真实的投射由于速度远低于平衡滑翔初始速度, 运动轨迹会在初始段变成跳跃式, 但是这种初始段的跳跃很快衰减成平稳下滑。平衡滑翔和真实低速投射状态的下滑轨迹相比具有更远的射程, 这是由于较高的速度等效于给滑翔注入了更多的动能。同样, 飞行器真实投射状态下的速度和下滑角在初始段的运动状态和平衡滑翔相比波动更剧烈, 但是其会迅速衰减到和平衡滑翔一样的运动状态直到落地。采用无约束最大升阻比滑翔的飞行方式, 在上述真实投射条件下, 着陆速度约为20 m/s, 着陆时速度倾角约为-8°, 最大滑翔距离136 km, 全程耗时约1h15min。
 |
图 3 飞行器投射受力分析简图 |
 |
图 4 飞行器加速状态 |
 |
图 5 最大升阻比下平衡滑翔与真实投射轨迹比较 |
3 滑翔轨迹优化
3.1 高斯伪谱法
前文对于下滑轨迹的分析基于使飞行器达到最远滑翔距离这一要求, 既使攻角固定在最大升阻比攻角。但在真实飞行任务中, 其具体目标会随着任务需求而改变, 此时需要通过控制使飞行目标最优化。对于最优控制问题, 用(12)式表示使其达到的性能指标
求解上述最优控制问题较为困难, 但伪谱法可将动力学方程的解表示为某种有限个基函数的和, 通过确定相应基函数的系数以保证在给定的有限个配点上等于真解从而求解动力学方程近似解。其中, 高斯伪谱法数学概念清晰, 所求KTT条件完全等价于高斯伪谱法离散连续Bolza问题的一阶必要条件所得到的离散化形式。高斯伪谱法可直接通过估算物理概念的初始条件从而避免勒让德伪谱法中猜测协状态的初始值, 降低了难度。并且, 微分形式下的高斯伪谱法由于矩阵稀疏, 通过适当算法可极大提高求解速度, 在局部收敛速率呈指数阶增长。高斯伪谱法的离散化节点分布在区间[-1, 1]上, 因此需要引入新的时间变量下τ进行变量变换, 变换式如下
性能指标(12)式经过转化可变为区间[-1, 1]上的标准形式
构造N阶Lagrange插值多项式
式中,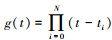 。
。
利用Li(t)的代数和, 可以构造任一函数f(t)在[-1, 1]上的一个N阶多项式形式的逼近函数
则f(t)的积分可由(16)式的逼近函数替换
式中,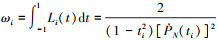 , i=0, 1, …, N称为高斯积分的权函数。
, i=0, 1, …, N称为高斯积分的权函数。
同样f(t)的导数同样可由(16)式的逼近函数替换
其在配点ti处满足
式中
应用(17)式将性能指标函数(14)式离散化为
同样应用导数(19)式在配点上将动力学状态方程离散化为
上式的离散化只针对配点, 而对于两端点有
过程约束和终端约束可离散化为
3.2 仿真分析
前文针对平衡滑翔投射条件和真实滑翔投射条件所得到的轨迹是一条无约束最远射程轨迹。对于其结果分析可以看到, 其落地时速度较快, 可能在落地时对飞行器造成损坏。并且在真实飞行任务中, 可能针对不同任务性质提出不同需求。在这里针对2种可能的需求使用高斯伪谱法研究最优滑翔轨迹特性。
第一种需求考虑目标函数为滑翔最长时间。此种任务需求对应于要求飞行器在滑翔过程中尽可能长的携带载荷完成空中任务的执行。并且考虑终端约束, 即落地时的终端速度小于10 m/s以减小其冲击力并且下滑角为0°使其可以平缓落地。目标函数表达如下:
性能指标:minJ=-tf
终端约束:Vf=10 m/s, θf=0°
第二种需求考虑其目标函数下滑时间最长的同时滑翔距离最远。此种任务需求对应于使载荷可以在降落的最远距离且同时尽可能长地停留在空中执行任务。并且在上述终端约束的条件下再加上滑翔时的过程约束, 即全程最大速度不大于50 m/s以减小可能的盘旋下降半径。其表达如下:
性能指标:minJ=-(tf+Rf)
过程约束:V≤50 m/s
终端约束:Vf=10 m/s, θf=0°
对于这两种需求, 其控制变量攻角的约束相同, 表达式如下:
控制约束:0°≤α≤16°
攻角的约束是基于文献[14-16]中对于不同平板翼型最大失速攻角的研究, 对于展弦比为2的平板翼型, 有效攻角小于16°。高斯伪谱法离散时配点数N取10对这2种目标的最优轨迹进行求解。
图 6给出了上述2种任务需求的高斯伪谱法优化结果。可以看到:对于第一种追求最长航时任务需求, 首先, 攻角作为控制变量仍然在绝大部分时间保持稳定, 但是稳定值7°要高于追求最远射程时的攻角4°。其次, 追求最长航时下的射程为116 km, 小于在最大升阻比下滑翔的最远射程136 km, 既追求了最远航时, 则其攻角所对应的升阻比不再是最大升阻比, 所以其射程会下降。由于追求最长下滑时间, 其航时比最远射程的时间增加了约8 min。最后, 对于终端约束, 主要体现在在最后着陆段0.6 km高度迅速增大飞行器的攻角到约13°, 从而减少冲击速度和角度, 使其满足着陆时的安全限制, 保护内部载荷。
对于第二种任务需求, 同时追求最远航时和最远射程, 可以看到:得到的最优轨迹最远射程与理论最远射程极为接近, 且航时也要比单纯追求最远射程长2 min。并且, 由于在此种需求中增加了对于最大速度的过程约束, 攻角作为控制量, 在初始段由一个较大的值逐渐减小以控制速度在初始段不大于50 m/s, 如图 6c)~6e)所示。如果不增加速度约束, 则其在初始段的最大速度峰值会超过80 m/s。在高度下降到约15 km时, 攻角趋于稳定不再减小, 稍高于追求最远航程时的攻角。着陆段同样在0.6 km时迅速增大攻角到约14°以提供安全限制。
 |
图 6 2种性能指标下仿真优化结果 |
3.3 优化结果可行性验证
前文优化结果是原问题使用Lagrange插值多项式近似后的离散解, 对于其可行性还需进行进一步验证。具体为将得到的控制变量作为输入带入到原动力学方程式(3)中进行积分, 比较积分后的结果和优化结果之间的误差。图 7展示了对上述第二种需求优化结果的验证, 可以看到其积分结果和优化结果吻合良好, 误差在合理范围内, 说明高斯伪谱法求解的最优控制变量是可行的。
 |
图 7 优化结果可行性验证 |
4 结论
本文对一种新出现的滑翔式微型飞行器进行了轨迹的分析和优化, 结论如下:
1) 对于无约束最大升阻比飞行(4°攻角), 初始投射状态满足平衡滑翔状态, 则下滑轨迹平缓, 但是真实投射装置无法达到平衡滑翔要求, 因此真实投射状态会使滑翔轨迹在初始段造成跳跃, 但是跳跃轨迹很快衰减成稳定的平衡滑翔状态。真实滑翔距离要比平衡滑翔距离少5 km。
2) 以最远航时为性能指标的优化轨迹在航时上要高于以最远射程为目标的航时约8 min, 但是射程会缩短约20 km。攻角在全程基本保持稳定在7°。以最远射程和最长航时同时为性能指标的优化轨迹在射程上接近理论最远射程136 km, 且高于原航时2 min。由于在过程约束中施加了速度约束, 攻角在初始段由大逐渐减小以控制全程速度不超过50 m/s。终端约束体现在当下降到0.6 km高度时开始迅速提高攻角到约13°以减缓速度和速度倾角。
3) 验证结果显示, 高斯伪谱法得到的优化轨迹具有良好的可行性。但是在实际计算过程中, 高斯初值和配点数的选取会对计算效率和收敛性产生影响。
References
- XiaoYongli, Zhang Chen. Study on Present Situation and Development of Micro Air Vehicles[J]. Journal of Astronautics, 1992, 18(5): 585–589 [Article] [Google Scholar]
- Hundley R O, Gritton E C. Future Technology-Driven Revolutions in Military Operations[R]. DB-110-ARPA, 1994 [Google Scholar]
- Waszak M R, Davidson J B, Ifju P G. Simulation and Flight Control of an Aeroelastic Fixed Wing Micro Aerial Vehicle[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, 2002 [Google Scholar]
- Grasmeyer J, Keennon M. Development of the Black Widow Micro Air Vehicle[C]//AIAA 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, 2001 [Google Scholar]
- Kahn A, Edwards D. Navigation, Guidance and Control for the Cicada Expendable Micro Air Vehicle[C]//AIAA Guidance, Navigation and Control Conference, 2012 [Google Scholar]
- Edwards D J, Kahn A D, Heinzen S B, et al. CICADA Flying Circuit Board Unmanned Aerial Vehicle[C]//2018 AIAA Aerospace Sciences Meeting, 2018 [Google Scholar]
- Laiacker M, Wlach S, Schwarzbach M. DLR High Altitude Balloon Launched Experimental Glider(Hableg): System Design, Control and Flight Data Analysis[C]//Workshop on Research, 2016 [Google Scholar]
- Yan Xiaodong, Tang San. Applying Pseudo-Spectral Method to Optimizing Entry Trajectory of Suborbital Launch Vehicle[J]. Journal of Northwestern Polytechnical University, 2010, 28(5): 748–752 [Article] [Google Scholar]
- Chen Xiaoqing, Hou Zhongxi, Liu Jianxia. Trajectory Characteristic of Hypersonic Gliding Vehicle[J]. Missiles and Space Vehicles, 2011, (2): 5–9 [Article] [Google Scholar]
- Li Ghuanghua, Zhang Hongbo, Tang Guojian. Typical Trajectory Characteristics of Hypersonic Glide Vehicle[J]. Journal of Astronautics, 2015, 36(4): 397–403 [Article] [Google Scholar]
- Gao Xianzhong. Research on High-Altitude Long-Endurance Flight of Solar-Powered Aircraft Based on Gravitational Potential and Wind Shear[D]. Hefei, National University of Defense Technology, 2014 (in Chinese) [Google Scholar]
- Shkarayev S V, Ifju P G, Kellogg J C, et al. Introduction to the Design of Fixed-Wing Micro Air Vehicles Including Three Case Studies[M]. American Institute of Aeronautics and Astronautics, 2007 [CrossRef] [Google Scholar]
- Vinh N X. Optimal Trajectories in Atmospheric Flight[M]. New York, Elsevier Scientific Publishing Company, 1981 [Google Scholar]
- Torres G E, Mueller T J. Low Aspect Ratio Aerodynamics at Low Reynolds Numbers[J]. AIAA Journal, 2004, 42(5): 865–873 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier A, Mueller T J. Low Reynolds Number Aerodynamics of Low-Aspect-Ratio, Thin/Flat/Cambered-Plate Wings[J]. Journal of Aircraft, 2012, 37(5): 825–832 [Article] [Google Scholar]
- Ananda G K, Sukumar P P, Selig M S. Measured Aerodynamic Characteristics of Wings at Low Reynolds Numbers[J]. Aerospace Science and Technology, 2015, 42: 392–406 [Article] [CrossRef] [Google Scholar]
- Okamoto M, Azuma A. Aerodynamic Characteristics at Low Reynolds Numbers for Wings of Various Planforms[J]. AIAA Journal, 2011, 49(6): 1135–1150 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Zipfel P H. Modeling and Simulation of Aerospace Vehicle Dynamics[M]. American Institute of Aeronautics and Astronautics, 2007 [CrossRef] [Google Scholar]
- Han Zipeng. Exterior Ballistics of Projectiles and Rockets[M]. Beijing, Beijing Institute of Technology Press, 2014 [Google Scholar]
- Ferreira L O. Nonlinear Dynamics and Stability of Hypersonic Reentry Vehicles[D]. Michigan, University of Michigan, 1995 [Google Scholar]
- Polhamus E C. Predictions of Vortex-Lift Characteristics by a Leading-Edge-Suction Analogy[J]. Journal of Aircraft, 1971, 8(4): 193–199 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 平板翼型不同翼面形状气动参数 |
| In the text | |
 |
图 2 平面再入坐标系变量关系 |
| In the text | |
 |
图 3 飞行器投射受力分析简图 |
| In the text | |
 |
图 4 飞行器加速状态 |
| In the text | |
 |
图 5 最大升阻比下平衡滑翔与真实投射轨迹比较 |
| In the text | |
 |
图 6 2种性能指标下仿真优化结果 |
| In the text | |
 |
图 7 优化结果可行性验证 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


