| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 992 - 999 | |
| DOI | https://doi.org/10.1051/jnwpu/20193750992 | |
| Published online | 14 January 2020 | |
Application of Improved Quantum Genetic Algorithm in Optimization for Surface to Air Anti-Radiation Hybrid Group Force Deployment
一种改进量子遗传算法在地空反辐射混编群兵力配置优化中的应用
1
Air and Missile Defense College, Air Force Engineering University, Xi'an 710051, China
2
Rocket Force University of Engineering Xi'an 710025, China
Received:
9
October
2018
In this paper, the concept and force deployment needs for anti-electronic jamming and defensing air of surface to air anti-radiation hybrid group was presented, the relationship between shield angle, deployment distance and effective electronic interference etc, were analyzed in the background of air raid battle which is with electronic support, force deployment optimization model of surface to air anti-radiation hybrid group was built based on the kill zone target function. In terms of the characteristic of hybrid group force deployment, quantum genetic algorithm (QGA) was improved with self-adaption rotation angle, the problem which was based on a living example was solved with improved QGA. By contrast, the improved QGA is better in the respects of global optimization, rate of convergence and stability than QGA, particle swarm optimization algorithm and quantum vortex algorithm in the problem of optimization for surface to air anti-radiation hybrid group force deployment.
摘要
提出了地空反辐射混编群概念及防电磁干扰与抗空中进袭的综合兵力配置需求,基于电子支援下的空袭作战背景,分析了掩护角、配置距离、有效干扰等要素的相互关系,并以杀伤区面积为目标函数,构建了地空反辐射混编群兵力配置优化模型。结合混编群兵力配置特点,对量子遗传算法进行了旋转角的自适应改进,在设置想定实例的基础上,运用改进的量子遗传算法对问题进行求解,并与传统量子遗传算法、粒子群算法和量子涡流算法计算结果进行了对比分析。结果表明:运用改进量子遗传算法求解地空反辐射混编群兵力配置优化问题,全局寻优能力更强、收敛速度更快、稳定性更好。
Key words: quantum genetic algorithm / surface to air ati-radiation / hybrid group / force deployment / Q-gate
关键字 : 量子遗传算法 / 地空反辐射 / 混编群 / 兵力配置 / 量子旋转门
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
地空反辐射导弹(SA-ARM)武器系统是利用空中目标电磁辐射获取探测识别、跟踪制导等信息, 并对目标实施拦截的地面防空装备, 其主要作用是为体系内其他信息化作战力量提供电子对抗的“保护伞”[1]。由于SA-ARM武器系统应对目标类型较为单一、对空中突击目标防护能力不强等特点, 在防空作战体系化趋于常态的背景下, 该武器系统与常规防空装备混编作战就成为必然。以SA-ARM武器系统为主体, 若干常规防空装备为配属组成的防空集群称为地空反辐射混编群, 在兵力组成既定的前提下, 常规防空装备如何配置才能发挥地空反辐射混编群整体火力, 既能实现对空中突防/击目标的有效拦截, 又能确保SA-ARM武器系统对防区外电子支援飞机的慑阻, 避免电子支援飞机对常规防空装备的有效干扰, 这已成为混编群作战运用亟待解决的问题。地空反辐射混编群兵力配置是典型的多约束决策问题, 既要求常规防空装备避免被有效干扰, 又要争取不同型号常规装备混合编组时, 通过合理的目标分配与火力运用对空袭编队的最大杀伤效能(杀伤目标数学期望最大化), 围绕该问题相关学者也进行了探讨, 文献[2]对地空反辐射导弹的功能性能特点进行了分析, 提出了其在防空作战体系中的作用及与常规防空装备混编编配的设想[2], 文献[3]阐述了地空反辐射导弹武器系统与常规防空装备混编作战的必要性及地空反辐射混成群内涵, 提出了兵力编组模式和混成群兵力部署的基本要求[3]。总体而言, 目前围绕该问题开展的研究偏少, 且其中定性论述居多、定量分析缺乏, 可供参考借鉴的成果不够。量子遗传算法(QGA-quantum genetic algorithm)是传统遗传算法中引入量子计算的产物, 与传统遗传算法相比, 量子遗传算法具有更好的种群多样性和并行计算能力, 其搜索范围更广、适应性更强、计算效率更高[4]。本文从地空反辐射混编群抗击空袭编队在掩护地面目标及反辐射导弹阵地对空安全、为常规防空装备提供电子防护等作战需求入手[3, 5], 构建了混编群兵力配置优化模型, 在提出一种改进的量子遗传算法基础上, 将该算法应用于地空反辐射混编群兵力配置优化问题, 并针对设定同型号常规防空装备兵力组成的地空反辐射混编群与作战对象, 直接生成可指导兵力配置的实施方案, 经仿真对比该算法全局寻优能力更强、收敛速度更快。
1 概念描述及关系分析
为便于开展地空反辐射混编群兵力配置优化分析, 在此引入空袭兵器完成任务线、压制性系数等有关概念。
1.1 概念描述
1) 空袭兵器可能完成任务线
敌空袭兵器可能完成任务线是指敌机或远射导弹为了使其空袭兵器有效毁伤保卫目标, 所必须到达保卫目标周围的一条界线, 通常用这一界线到保卫目标中心的水平距离来表示。如果在此界线前将空袭目标消灭, 则不会给保卫目标造成伤害, 在此界线后即使将空袭目标消灭, 仍会给保卫目标造成伤害[6], 空袭兵器可能完成任务线如图 1所示。
2) 压制性系数与有效干扰
电子干扰压制性系数Kj是指电子干扰设备对防空武器火控雷达实施有效干扰即在搜索状态下雷达发现概率下降到0.1以下时, 雷达接收机输入端所需要的最小干扰信号与雷达回波信号功率之比。从定义来看, 压制性系数越小, 雷达抗干扰能力越弱, 越容易被干扰; 反之, 压制性系数越大, 雷达抗干扰能力越强, 越不易被干扰。利用压制性系数可以推导出干扰方程
式中, Pγs为雷达收到的目标回波信号, Pγj为进入雷达接收机的干扰信号, Pj, Pt分别为干扰机和雷达的发射功率, Gj, Gt分别为干扰机和雷达的天线增益, γj为干扰信号对雷达天线的极化系数, σ为目标的雷达截面积, G′t为雷达天线在干扰机方向上的雷达天线增益, Rt, RJ分别为目标与雷达的距离及干扰机与雷达的距离[7-7]。
3) 掩护角
防空武器对保卫目标的掩护角, 是一个以保卫目标中心为顶点的扇面角, 配置在保卫目标周围的防空武器可以将从该扇面角范围内临近保卫目标飞行的敌机消灭在其可能完成任务线之前[9]。掩护角2ϕ的大小与敌机可能完成任务线到保卫目标中心的水平距离drwx、杀伤区的远界水平距离dsy、防空武器相对于保卫目标中心的水平距离dpz有关。
式中,h0为相邻杀伤区火力衔接部分在可能完成任务线外的杀伤区纵深, 这里设h0=dsy+dpz-drwx, 那么(2)式转变为
 |
图 1 SA-ARM杀伤区远界与常规防空装备配置距离及电子干扰机最远作用距离的关系 |
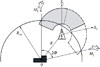 |
图 2 掩护角的物理意义 |
1.2 相关概念关系分析
1) 配置距离与水平杀伤区面积
鉴于地空反辐射混编群承担任务的性质, 这里假定电子干扰机对混编群内常规防空武器的压制性系数为7(雷达抗干扰能力为中等量级)。为避免地空反辐射武器攻击, 空中干扰机一般在地空反辐射武器杀伤区远界绕飞施放干扰, 因此, 地空反辐射武器杀伤区远界Dffssy、常规防空武器配置距离dipz及干扰机与常规防空武器制导雷达的距离RJ满足以下关系
因为Dffssy是一个定值, 将(4)式代入(1)式, 经转化常规防空武器配置距离dipz与制导雷达最大搜索距离Rt(目标与雷达的距离)就形成了一一对应关系即
依据经验制导雷达最大搜索距离与水平杀伤区面积S有以下函数关系
式中,k, q均为常数, Diwgrsj, Diwgrsy分别为第i个常规防空武器无干扰条件下水平杀伤区近界和远界, Rt, Diwgrss分别为有、无干扰条件下制导雷达的最大搜索距离。
将(5)式代入(6)式, 经转化得到杀伤区面积与常规防空武器配置距离的函数关系式
2) 配置距离与可能完成任务线
设第i个常规防空武器配置距离(与保卫目标的距离)为dipz、杀伤区远界为Disy, 为了能在空袭目标到达可能完成任务线之前将其有效杀伤, 常规防空武器配置位置距保卫目标距离与杀伤区远界的和应大于空袭目标可能完成任务线的水平距离drwx, 即dipz+Disy>drwx。
3) 责任扇区与掩护角
责任扇区是地空反辐射混编群承担防空任务方向的界定, 在水平面上为一个扇面角θ, 在此扇面角范围内的所有空袭目标由地空反辐射混编群拦截射击。混编群内常规防空武器若要实现以不低于指定概率对责任扇区内来袭目标进行拦截, 须满足常规防空武器对地面保卫目标掩护角之和不小于地空反辐射混编群防空责任扇区即: , 为确保防空火力资源的有效性, 这里设定
, 为确保防空火力资源的有效性, 这里设定 , 且地空反辐射导弹武器系统工作扇区可覆盖混编群防空责任扇区。
, 且地空反辐射导弹武器系统工作扇区可覆盖混编群防空责任扇区。
4) 叠加杀伤区面积与综合作战效能
定性来说, 在地空反辐射导弹武器系统掩护下, 常规防空武器若要实现对来袭目标杀伤效能最大化, 需令叠加后的常规防空武器杀伤区面积最大。这里设定常规防空武器杀伤区火力衔接时, 水平杀伤区重叠部分面积占单个常规防空武器杀伤区面积的5.2%(经验值)。
随着常规防空武器配置前伸, 其被干扰强度逐渐增强, 对空袭目标最大搜索距离逐步减小, 水平杀伤区面积逐渐压缩, 导致混编群综合杀伤效能不断下降。如何在满足相关限制条件的同时, 令地空反辐射混编群内常规防空武器的水平杀伤区面积最大, 就成为该问题的求解目标。该问题也就转变为多参数、多条件下的决策优化问题[6-6]。
2 兵力配置优化模型
为建立地空反辐射混编群兵力配置优化数学模型, 作如下简化想定:某地空反辐射混编群配属1套SA-ARM武器系统、3套同类型常规防空武器, 用以承担某要地指定方向的对空防御任务, 责任扇区扇面角为100°, SA-ARM武器系统工作扇区可覆盖责任扇区, 敌对方空袭编队在电子干扰飞机支援下实施突防(击)。在SA-ARM阵地位置已定的情况下, 3套常规防空武器如何配置可使作战群对空防御作战效能最大, 如图 3所示。将问题置于以地空反辐射阵地为原点的平面直角坐标系内进行讨论, 第i套防空武器的配置位置为(xi, yi), 则其配置距离为 。根据上述分析地空反辐射混编群兵力配置优化的目标函数为
。根据上述分析地空反辐射混编群兵力配置优化的目标函数为
同时, 还应满足以下约束条件
θi≠θi+1≠θi+2≠…θi+n, i=1, 2, 3(常规装备配置点方位角互不相等)
因为
将(11)式分别代入(9)式和(10)式, 则约束条件转变为关于配置距离dipz的2个约束。
 |
图 3 常规防空武器兵力配置示意图 |
3 量子遗传算法的改进
量子进化算法利用量子理论中有关量子态的叠加和纠缠等特性, 通过量子并行计算来求解问题, 其计算特性和硬件基础使得量子进化算法拥有巨大的潜力。文献[17]提出了具有细胞结构种群的去中心化的量子粒子群算法。算法重新定义了每个子种群搜索方式, 通过将子种群最优个体与固定范围的局部粒子进化的方式进行搜索。文献[18]通过设置一种自适应邻域变化的方法, 将克隆机制引入量子进化算法中。文献[19]针对实时车间调度问题, 提出了启发式量子进化算法, 算法使用基于剪枝交叉方法提高种群的多样性。上述文献主要的改进在于通过改变算子搜索方式进而避免算法陷入局部最优, 但是这些算法的计算复杂度较高, 理解和实现难度相对较大。本文基于基本量子遗传算法, 提出了自适应旋转门搜索方式。该方法依据每个个体在种群中偏离最优个体的程度, 自适应生成旋转门, 在保证种群多样性和避免搜索陷入局部最优的同时, 最大化提高收敛速度, 且与其他文献相比, 本文方法计算简单、复杂度低、易于实现[11-11], 这与地空反辐射混编群防空作战规划高时效性与简构性要求是相契合的[3, 6]。
3.1 量子遗传算法简述
在量子遗传算法中最重要的是量子编码和量子门的引入。量子编码是将染色体用量子的态矢量表示, 使一条染色体表达为多个态的叠加, 从而增加了种群的多样性和丰富性, 使算法能够在较小的种群规模下寻优; 而量子门的引入确保了种群的更新, 使算法能够快速收敛。
1) 量子比特编码
在量子计算中量子比特是最小的信息存储单元, 一个量子比特可用3种状态来表示, 分别是0态、1态及0, 1之间的任意叠加态, 其状态表达式为
式中, α和β(复数)为量子比特对应的概率幅, |0〉的概率为α2、|1〉态的概率为β2, 且两者满足关系式
在QGA中用一对复数表达一个量子比特, 具有n个量子比特的系统可用如下方式表示
式中,αi2+βi2=1, i=1, 2, 3…n。用这种方法来定义染色体, 可使一条染色体同时表达多个态的叠加, 从而实现了用较小的种群规模表达更多信息的目的。
2) 量子门
量子门是进行量子比特的操作机构, 随着QGA的不断发展演进, 目前量子门也有多种类型。本文采用量子旋转门实现染色体的调整。量子旋转门相当于传统遗传算法中的变异, 其调整操作为
式中, θi为旋转门的旋转角, 其大小和方向取决于选定的调整策略, θi过大则染色体更新幅度增加, 易导致未全局寻优即收敛, θi过小则染色体更新幅度减小, 易导致局部寻优。由此可见, 旋转角的取值策略对问题求解具有重要影响。
3.2 算法的改进
为实现算法的改进, 此处引入自适应调整量子旋转门旋转角的思想, 在种群保留和更新之间寻找一个平衡点, 以避免早熟和局部寻优情况的出现。基本考虑是, 在染色体距当前最佳适应度值较远时, 适当增大旋转角, 以提高染色体更新幅度, 强化全局寻优能力; 在染色体距当前最佳适应度值较近时, 适当减小旋转角, 以提高算法收敛速度。具体方法为:以当前目标函数值对最优值之比为旋转角增减率的依据, 确定旋转角基准值后旋转角随之确定, 即
式中, θm为旋转角基准值、f为当前目标函数值、fmax为每次计算的最优目标函数值。
旋转角取值范围一般在0.001~0.1π之间[11], 鉴于地空反辐射混编群所属装备射程范围广、兵力配置位置可选范围大, 为强化算法的全局寻优能力及收敛速度, 需适当加大旋转角步进值, 因此这里θm取最大值0.1π, 改进量子遗传算法流程如图 4所示。
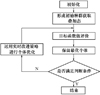 |
图 4 改进量子遗传算法流程 |
4 实例分析
现设置作战场景典型参数, 运用改进的量子遗传算法对问题求解, 并对结果进行分析。
4.1 场景设定
为更好地说明问题设置想定实例, 假设Dffssy为410 km, σ为2 m2, γj为0.5, drwx为140 km, Diwgrss为150 km, Diwgrsy, Diwgrsj分别为120, 4 km, Gt, G′t, Gj分别为35, 15, 13 dB, Pj, Pt分别为1和100 kW, 2个常数k=0.88, q=1.12, 将以上数值代入后得目标函数与约束条件如下
在约束条件中, 对于2个不等式约束(G1和G2)和一个不等式约束(G3), 采用罚函数的方法, 将约束条件与目标函数一并处理, 对于不等式约束θ1≠θ2≠θ3则是将不满足约束条件的个体剔除。
本文的问题为最大值求解问题, 鉴于目标函数的数值范围与约束条件的数值范围差异较大, 因此采用自适应罚函数控制方法进行求解。
式中, 惩罚系数自适应更新如下:
式中, λ(t)表示第t代的罚函数, η1和η2分别表示迭代过程中惩罚系数变化参数, case #1表示在过去g代中, 最优个体均为不可行解, case #2表示在过去g代中最优解为可行解。其原理可理解为:若在此之前所找到的最好个体均为可行解, 则表明惩罚系数已足够大, 可适当减少来降低对不可行解的惩罚压力; 若此前所找到的最好个体均为不可行解, 则表明惩罚系数过小, 需适当增大来增强对不可行解的惩罚力度。在实例求解中, η1和η2分别设为3和2, g设为5。
4.2 问题求解及结果分析
为了对兵力配置优化模型进行验证, 并开展实验结果分析, 分别采用本文提出的改进量子算法、基本量子算法、粒子群算法及量子涡流算法对问题进行计算。其中, 粒子群算法的加速因子c1和c2设为2, w取值0.729, 量子涡流算法和基本的量子算法除了种群规模没有额外的参数, 本文算法的主要参数是θm设为0.1。每种算法在算例中种群规模N设为100, 迭代终止次数设为100, 4种算法第一次运行时最优解在迭代过程中的变化过程如图 5所示。
表 1为第一次运行得到的对应最佳目标函数值的常规防空装备配置位置, 对照地空反辐射混编群作战部署要求[3], 随机遴选若干组配置位置进行验证, 定性对比结果证明了模型及算法在地空反辐射混编群兵力配置问题求解方面的有效性。图 5中, 从算法搜索最优解的趋势可以看出, 本文算法在前期能够搜索到精度相对较高的最优解, 而其他算法的搜索能力较差。尽管量子涡流算法能够很快搜索出与本文算法精度相似的最优解, 但是最后的局部搜索结果中, 本文算法要优于量子涡流算法。为了进一步验证算法的优越性, 4种算法在案例中独立运行50次, 计算最优值的均值和方差, 结果如表 2所示。从表 2可以看出, 本文的算法在收敛精度和稳定性方面要优于其他3种算法。这充分体现了改进QGA算法的优越性。
由表 3可看出, 本文算法在运行时间上均劣于其他3种算法, 运行50次, 其周期均值达0.161 2 s, 考虑到兵力配置往往在战前开展, 因此对问题分析而言该运行时间可控, 能够满足实际需求。
 |
图 5 最优解与迭代次数关系图 |
地空反辐射混编群常规装备配置位置
目标函数值对比
运行时间对比
5 结论
量子遗传算法以其先进的结构设计和运行模式, 自提出伊始就展现了其在多目标多条件问题求解中的独特优势。本文构建了地空反辐射混编群兵力配置优化模型, 并结合混编群兵力配置特点, 对QGA旋转门旋转角设置进行了自适应改进, 经开展简化实例(同型号常规防空装备、等杀伤概率杀伤目标)计算及对比分析, 证明了混编群兵力配置优化模型的有效性及改进QGA在兵力配置优化问题求解中的优越性, 计算结果可直接应用于兵力配置实践。结合问题实际, 后续可在量子比特编码、异型常规防空装备目标分配、自卫式干扰目标拦截等环节上进行改进完善, 如引入量子灾变等思路, 进一步强化算法的全局寻优能力。
References
- GuErshun. Surface to Air Anti-Radiation Missile Analysis and Research[J]. Surface to Air Weapon, 2010, 1: 19–22 [Article] [Google Scholar]
- Liu Yili. Analysis of Surface to Air Anti-Radiation Missile System's Effect[J]. Recent Manufacture Technology and Equipment, 2016, (3): 152–154 [Article] [Google Scholar]
- Ji Junliang, Duan Libo, Tian Hailin. Research on Surface to Air Anti-Radiation Hybrid Group Force Deploy[J]. CruiseMissile, 2017, (1): 49–54 [Article] [Google Scholar]
- Hkh K J H. Genetic Quantum Algorithm and its Application to Combinatorial Optimization Problem[C]//Proc of IEEE Congress on Evolutionary Computation, 2000: 1354–1360 [Google Scholar]
- Xia Hui. Review of the USA Navy Carrier-Borne EW Aircraft[J]. Electronic Information Warfare Technology, 2014, (6): 19–22 [Article] [Google Scholar]
- Chen Hongyou, Guo Youquan, Wang Yinglong. Air Force Surface to Air Missile Army Tactics[M]. Beijing, PLA Publishing House, 2015 [Google Scholar]
- Zhang Yongshun, Tong Ningning, Zhao Guoqing. Radar Electronic Warefare Theory[M]. Beijing, National Defence Industrial Engineering Publishing House, 2015 [Google Scholar]
- Tao Huan, Zhou Xiaoping, Sun Yongquan, et al. An Evaluation Method of Electronic Jamming Signal Environment Based on SJR[J]. Journal of Terahertz Science and Electronic Information Technology, 2017, (1): 59–64 [Article] [Google Scholar]
- Lu Yingqi, Li Ning, Chen Gang. Covering Angle Analysis of Anti-Missile Deployment[J]. Fire & Command and Control, 2015, (7): 85–88 [Article] [Google Scholar]
- Kou Zhanlin. Shoot Theory and Application of Surface to Air Missile[M]. Xi'an, Air Force Engineering University, 2014 [Google Scholar]
- Bai Xiaobao. Reaearch on Quantum Genetic Algorithm[J]. Exploitation and Applitation of Computers, 2013, (1): 9–15 [Article] [Google Scholar]
- Jiang Linli. Summarization of Quantum Genetic Algorithm Research Actuality[J]. Journal of Guangxi Science & Technology Normal University, 2016, (2): 130–133 [Article] [Google Scholar]
- Liang Changyong, Bai Hua, Cai Meiju, et al. Advances in Quantum Genetic Algorithm[J]. Application Research of Computers, 2012, (7): 2401–2405 [Article] [Google Scholar]
- Yang Ying. Analysis of Logistics & Manufacture Intergrowth Stage based on Quantum Genetic Algrithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(2): 69–73 [Article] [Article] [Google Scholar]
- Yu Wangle, Wang Jiaquan. Application Research on Complex Water Quality Prediction with Improved QGA-BP Model[J]. PR & AI, 2012, (4): 705–708 [Article] [Google Scholar]
- Ma Yongjie, Yun Wenxin. Research Progress of Genetic Algorithm[J]. Application Research of Computers, 2012, (4): 1201–1206 [Article] [Google Scholar]
- Fang W, Sun J, Chen H, et al. A Decentralized Quantum-Inspired Particle Swarm Optimization Algorithm with Cellular Structured Population[J]. Information Sciences, 2016, 330: 19–48 [Article] [CrossRef] [Google Scholar]
- Liu J, Wang H, Sun Y, et al. Adaptive Niche Quantum-Inspired Immune Clonal Algorithm[J]. Natural Computing, 2016, 15(2): 297–305 [Article] [CrossRef] [Google Scholar]
- Konar D, Bhattacharyya S, Sharma K, et al. An Improved Hybrid Quantum-Inspired Genetic Algorithm(HQIGA) for Scheduling of Real-Time Task in Multiprocessor System[J]. Applied Soft Computing, 2017, 53: 296–307 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 SA-ARM杀伤区远界与常规防空装备配置距离及电子干扰机最远作用距离的关系 |
| In the text | |
 |
图 2 掩护角的物理意义 |
| In the text | |
 |
图 3 常规防空武器兵力配置示意图 |
| In the text | |
 |
图 4 改进量子遗传算法流程 |
| In the text | |
 |
图 5 最优解与迭代次数关系图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


