| Issue |
JNWPU
Volume 43, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 128 - 139 | |
| DOI | https://doi.org/10.1051/jnwpu/20254310128 | |
| Published online | 18 April 2025 | |
Multi energy dynamic soaring trajectory optimization method based on reinforcement learning
基于强化学习的多能源动态滑翔航迹优化方法
1
School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China
2
The Science and Technology on Aircraft Control Laboratory, Beihang University, Beijing 100191, China
3
Hiwing Aviation General Equipment Co., Ltd., Beijing 100074, China
Received:
6
March
2024
In addressing the issue of dynamic soaring in unmanned aerial vehicles, a trajectory optimization approach based on deep reinforcement learning is proposed. This method synergistically utilizes gradient wind energy and solar energy and incorporates obstacle constraints to simulate complex barrier environments. It employs neural networks to approximate the Gaussian pseudospectral method for solving trajectory policies. On the foundation of the trained policies, the method utilizes the twin delayed deep deterministic policy gradient algorithm for policy enhancement. This significantly boosts the real-time inference capabilities while addressing the challenges traditional optimal control algorithms face in dynamic soaring due to varying wind fields. The experiments initially validate the approach through simulation of two classic modes of dynamic soaring, followed by Monte Carlo simulations considering multiple energy sources. The results indicate that the dynamic soaring trajectory optimization method based on deep reinforcement learning achieves energy acquisition comparable to optimal outcomes within a single soaring cycle, with a 91% reduction in real-time inference decision time. Moreover, in changing wind field environments, this method demonstrates superior adaptability compared to traditional approaches.
摘要
针对无人机动态滑翔问题, 提出了一种基于深度强化学习的航迹优化方法。该方法综合利用梯度风能和太阳能, 引入了障碍物约束以模拟复杂障碍环境。使用神经网络近似逼近高斯伪谱方法求解航迹的策略, 在训练得到的策略基础上利用双延迟深度确定性策略梯度算法进行策略改进, 在大幅度提升推理实时性的同时解决了传统最优控制算法在动态滑翔领域难以应对变化风场的问题。实验针对动态滑翔2种经典模式进行仿真验证, 之后在考虑多种能量源的情况下进行蒙特卡洛仿真。结果表明, 基于深度强化学习的动态滑翔航迹优化方法在单个滑翔周期内获能与最优结果相近, 而实时推理决策时间减少了91%。在变化风场环境下, 文中方法相较于传统方法具有更强的适应性。
Key words: dynamic soaring / reinforcement learning / Gaussian pseudospectral method / trajectory optimization
关键字 : 动态滑翔 / 强化学习 / 高斯伪谱 / 航迹优化
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
动态滑翔是信天翁使用的一种近似无动力的飞行模式, 采用该模式可以使它们在消耗最少能量的前提下进行长距离飞行。在一个存在梯度风场的环境中, 信天翁通过“逆风爬升, 顺风下滑”机制在风切变层之间穿梭获取能量从而实现长时间滞空[1]。由于信天翁在动态滑翔过程中其翅膀始终保持伸展状态, 与小型固定翼无人机类似, 因此研究人员尝试将这一机制迁移到后者从而有效地提升飞行器的航时和航程[2]。作为动态滑翔的核心问题, 航迹优化需要综合考虑风场信息和无人机动力学特性, 并在此基础上规划出一条可飞的周期性航迹。它是探索动态滑翔机理和进一步应用的关键技术和难点问题。另一方面, 环境中不仅存在风能, 还存在其他能量例如太阳能, 如何在考虑多种能源的前提下进行航迹优化具有广阔的研究前景。
固定翼无人机的动态滑翔航迹优化问题可以归结为一个最优控制问题, 即在满足无人机动力学约束和环境约束的前提下求解代价函数的最值。根据任务目标不同, 优化目标可以是最小化参考风速、最大化无人机获能、最大化航时等[3]。在解决这类问题时, 大多数学者采用了多重打靶法、解析法、直接配点法、微分平坦法和高斯伪谱(Gaussian pseudospectral, GP)等[4–7]的最优控制方法。但在使用这类方法时存在求解复杂度较高、实时性较差的问题。文献[8]对比了上述常见的用于动态滑翔航迹优化的最优控制方法, 结果表明在设置51个配点的情况下, 使用直接配点法的优化耗时不足2 s, 相较于相同条件下的微分平坦法和高斯伪谱法优化速度更快, 然而高斯伪谱法却具有更高的求解精度。文献[9]考虑到传统方法耗时较长, 无法实时根据风场信息修正优化航迹, 提出了一种基于凸二次规划的动态滑翔航迹优化方法。但在推导过程中使用到了较多的假设, 过程较复杂, 当风场模型不一致时需要重新对问题进行凸化, 普适性存在一定欠缺。也有一部分学者尝试采用随机树算法进行航迹优化[10], 有效地满足了局部规划实时性的要求, 但当规划航迹较长时其耗时依旧不满足要求。更为关键的是, 随机树无法保证解的唯一性和最优性。
强化学习(reinforcement learning, RL)是一种机器学习范式, 旨在通过智能体与环境的大量交互来使智能体学习某种期望具有泛化性的策略, 具有一次训练、多处使用的特点[11]。传统方法是在滑翔前直接优化控制量序列, 若在滑翔过程中环境变化将导致优化航迹不可用。强化学习的出现为实时动态滑翔优化给出了解决思路: 动作网络可以根据当前环境给出合理的控制量且每一时刻都会针对环境做出变化。Li等[12]讨论了如何使用近端策略优化(proximal policy optimization, PPO)求解圆形航迹的动态滑翔问题。文献[13]采用无模型(model free, MF)框架的强化学习算法并取得了初步结果, 证实了此方向的可行性。然而Montella[14]指出动态滑翔问题解的搜索空间过大, 直接采用强化学习算法难以使智能体学习到最优策略, 并提出了基于模仿传统算法决策的“示教控制器”进行强化学习训练的解决思路, 很好地解决了动态滑翔在训练初始阶段难以搜索到可行解的问题。但Montella给出的方案中求解场景较为单一且使用到的强化学习算法较为简单。
由于环境中不仅存在风能, 还存在其他能源例如太阳能等, 动态滑翔过程中可以考虑更多能量来源以进一步延长航时。现有大多文献仅考虑了从各种环境风场中获能, 少数学者探索了太阳能和风能结合的情况, 但缺少综合分析[15–16]。考虑将太阳能纳入动态滑翔优化范围内会使优化情况变得更加复杂, 此时无人机还需要倾向于将太阳能板垂直于光线入射方向, 因此优化结果可能不再满足“逆风爬升, 顺风下滑”。
现有关于动态滑翔航迹优化问题研究取得了丰硕的成果, 但存在以下问题: ①传统最优控制方法需要离线生成航迹, 如果环境风场在后续跟踪控制过程中变化, 无法针对变化对航迹进行在线修正。采用强化学习的方法可以解决实时性的问题, 但是存在训练初期难以收敛的情况。②现有针对多能源结合的动态滑翔航迹优化研究较少, 大部分仅考虑了梯度风场获能。③现有方案在求解动态滑翔问题时没有考虑到障碍物约束, 而在实际应用场景下可能存在部分以建筑物为代表的障碍。
针对以上问题, 本文针对多能源综合利用下的固定翼无人机动态滑翔航迹优化问题, 借助双延迟深度确定性策略梯度算法(twin delayed deep deterministic policy gradient, TD3)[17], 提出了一种基于强化学习的航迹优化算法。该算法主要创新点为: ①引入了动态滑翔障碍物约束用以模拟具有障碍物的环境；②给出了多能源综合利用下动态滑翔问题建模并对获能机理进行了分析, 同时针对该问题设计了相应的强化学习交互模型；③利用深度神经网络学习最优控制算法根据环境信息规划航迹的策略, 作为后续训练的“指导者”, 为提升实时性奠定基础；④给出了基于“指导者-执行者”的强化学习两阶段训练步骤, 用以解决动态滑翔问题搜索空间大, 难以训练的问题。
1 风场环境及无人机运动学建模
1.1 梯度风场模型
固定翼无人机动态滑翔主要从海平面、地面上方数十米位置的侧向梯度风场中获取额外能量, 因此本文使用近地表面(海面, 地面或者山脊)风场常用的指数梯度风场模型, 表达式为[18–19]:
式中: HR表示某一给定高度; VR表示在给定高度下对应的实际风速, VR决定了风剖面内的整体梯度和平均风速的大小; Vw, x, Vw, y指风场中侧向风速在x轴和y轴的分量; 指数p为风场强度变化指数, 表征梯度风场的变化强度; ew为风速与x轴的夹角。
1.2 动态滑翔航迹优化模型
根据文献[20–21], 本文给出包含空间变化风场的无人机运动学模型。在东北天坐标系下各变量关系如图 1所示。
 |
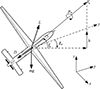图1 动态滑翔简化模型坐标系及变量之间关系示意图 |
式中
式中, 有6个状态变量和3个控制变量, 其中包括东、北、天3个位置(x, y, h), 空速Va, 气流航迹爬升角γa和气流航迹方位角χa。μa为气动滚转角, 以描述升力L绕空速Va的转动。模型假设升力系数CL和气动滚转角μa可以直接给定, 并与飞行器推力T一同构成模型虚拟控制输入。飞行器质量为m。三轴风速及风加速度为Wx, Wy, Wh和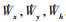 
。L为升力, D为阻力。升力与阻力的计算采用简化模型(4)式表示。
式中：ρ代表空气密度; CL和CD分别是升力系数与阻力系数; CD0为零升阻力系数; KD为诱导阻力因子; S为机翼面积。
1.3 太阳能模型
本文除考虑无人机从梯度风场中获能外, 还考虑太阳能获取, 对太阳能的辐射强度进行建模。首先根据相关文献[22]可知太阳垂直照射下的强度
式中：I=1 367 W为太阳常数; ε=0.017 7为地球偏心率; nd为计算照射强度当天与当年1月1日的日期差, 单位为天。
要计算太阳能的辐射强度, 需要确定当地日地连线矢量ns的方向
式中：βs为太阳高度角; γs为太阳方位角, 光线朝向正东时方位角为0, 向南偏转时取正; φs为赤纬角; θs为地理纬度; ωs为太阳时角; tmission为一天中的时刻。
容易分析, 当日地连线向量ns与固定翼无人机机翼平面的法向量nw的夹角越接近于180°时, 太阳能辐射吸收效率越大。根据几何关系, 有太阳能原始功率Psun0为
式中，〈ns, nw〉表示ns与nw之间的夹角。原始功率需要经过一系列的传递单元最终才能转化为机械能, 其中涉及到动力系统的能量耗散。因此, 最终太阳能通过动力系统转化为机械能的功率Psun
式中：ηsc为光伏电池转化为电能的效率; ηasc为光伏电池在机翼上铺设的面积与机翼面积的比值; ηm为能源管理系统的效率; ηp为推进系统的效率。
当π/2 < 〈ns, nw〉≤π时, 将(7)式重新表示为
式中
(9) 式中cos〈ns, nw〉的表达式为
式中
式中，ψ, θ, φ分别为偏航角、俯仰角和滚转角, 本文中偏航角的定义以y轴为基准, 向x轴转动为正。
2 动态滑翔最优控制问题
动态滑翔航迹优化问题的本质可归结为一个包含微分方程约束、过程约束、终端约束的最优控制问题。其中微分方程约束受到航迹优化运动学方程影响, 终端状态约束受到动态滑翔模式影响, 过程约束受到无人机姿态和滑翔范围等因素影响。在进行最优控制问题建模前, 本文将首先分析动态滑翔问题的获能机理, 为后续目标函数构建奠定基础。
2.1 气流系下动态滑翔获能机理分析
应用动态滑翔技术的小型太阳能飞行器飞行过程中主要的能量来自风场中获取的能量EW和经由太阳能动力能源系统获得的太阳能Esun; 主要的能量支出为空气阻力带来的能量损失ED和动力系统做功消耗的能量ET, 其中ET消耗的能量会补充飞行器的机械能。
固定翼无人机的动力学往往与无人机的空速相关, 因此相对于气流的能量往往能代表无人机在风场环境下的有效能量。定义气流系下固定翼无人机的总能量为相对于气流的动能与重力势能之和[23], 如(14)式所示。
因此, 能量的变化率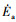 
为
进一步地, 结合动态滑翔模型得
为了简化动态滑翔获能机理的分析, 假设环境中只存在沿x轴水平的梯度风场[3]。由于指数梯度风场的大小只与高度h相关, 则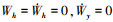 
, 又根据 
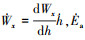可简化为
式中：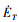
表示发动机推力产生的对飞行器的正功率；
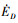表示无人机在飞行过程中阻力产生的功率消耗；
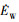代表无人机从梯度风场中获取的能量功率。
2.2 动态滑翔问题约束建模
对于过程约束, 主要考虑到动态滑翔无人机本身的一些特性, 首先是空气动力特性带来的升力系数、最大爬升角、空速和气动滚转角限定为
除此之外, 无人机的重心要保持一定的安全高度，即
进一步, 为了避免无人机机翼和水平面相碰撞, 引入对翼尖间隙的约束
同时, 考虑到动态滑翔所处环境中可能存在诸多障碍物, 为保证无人机不与障碍物碰撞, 引入对状态x, y, h的过程约束。为简化起见, 障碍物以球形为代表，如(21)式所示。
式中：(Oix, Oiy, Oih)表示球形障碍物球心；Ri为第i个障碍物球半径；N为障碍物个数。
对于终端约束, 不同模式的动态滑翔不尽相同。闭合模式的动态滑翔常针对环绕监视的任务场景, 其要求无人机优化出来的航迹起始点和终止点状态一致，如(22)式所示。
而行进模式下要求无人机在动态滑翔过程中向着某个特定方向前进。其终端约束如下
式中：ε表示了行进模式下无人机的前进方向。若动态滑翔模式为自由行进式, 则(23)式没有最后一项。
2.3 能量建模和代价函数构建
综合考虑同时利用多种能量构建最优控制代价函数:
1) 由无人机推力带来的能量消耗功率
2) 由无人机受到的阻力产生的能量消耗功率
3) 无人机动态滑翔过程中从风场获取能量的功率
4) 无人机动态滑翔过程中获取的太阳能功率Psun。
综上所述, 衡量总体能量收支变化率的最终表达式为
在本文中, 最优滑翔的目的是在单个滑翔周期内获取最多的能量。因此, 最优控制问题代价函数建模为
3 基于强化学习的动态滑翔优化
使用强化学习解决动态滑翔问题首先需要考虑如下问题: ①动态滑翔动作量均为连续动作, 相较于离散动作更难搜索; ②滑翔区域较大, 受各种约束, 同时还要考虑多种能量获取; ③整个训练回合可能需要上千步推理迭代。以上3点导致强化学习算法所需搜索的解空间范围较大。因此Montella等[24]指出需要优先提供一个“指导者”来模仿某一传统方法得到的航迹生成策略, 再利用强化学习在“指导者”的参考指令下进行训练学习, 获得“执行者”。根据此思路, 本文设计了基于深度强化学习的固定翼无人机动态滑翔航迹优化算法框架如图 2所示, 其分为3个阶段: ①“指导者”离线训练阶段: 利用神经网络拟合传统最优控制方法在动态滑翔问题上的优化策略。本文选用了相较于直接配点法精度更高的高斯伪谱方法求解大量不同的动态滑翔问题, 并将对应的状态-控制量序列放入样本池。之后“指导者”神经网络学习从状态量到控制量的映射策略; ②“执行者”离线训练阶段: 引入强化学习, 在相同的环境下进行学习, 不同的是状态量将同时输入“指导者”网络和强化学习“执行者”网络, 之后“执行者”网络的输出将作为“指导者”网络输出的偏置项最终作用在环境中; ③在线使用阶段: 无人机在动态滑翔过程中在线使用“指导者”网络和“执行者”网络, 并将两者输出结合作用于环境获得新的滑翔方向。在这个过程中并没有耗时的最优控制算法参与, 且推理过程采用单步迭代的方式, 从而解决了实时性问题。
 |
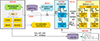图2 基于深度强化学习的固定翼无人机动态滑翔航迹优化算法框架 |
3.1 基于深度神经网络的“指导者”训练
“指导者”的作用在于为强化学习智能体提供训练初期的引导策略, 考虑到问题的复杂性和其本身的定位, 这种引导策略无需十分准确。本文设计了较为简单的多层感知机(multi-layer perceptron, MLP)用以拟合高斯伪谱法在动态滑翔问题上针对不同场景下的航迹生成策略。在图 2中, 首先需要在不同场景下收集大量高斯伪谱法解算得到的状态-控制轨迹，如(29)式所示。
式中：i表示样本编号；tc(i)表示控制量作用时间；N为样本总数。之后利用深度神经网络对样本集(X, Y)进行拟合, 网络将有能力输出风场环境中某一状态下无人机需要的虚拟控制量。训练得到的网络被用于之后深度强化学习训练中，并在其基础上进行策略的优化。
3.2 基于双延迟确定性策略梯度算法的“执行者”训练
本文使用TD3作为动态滑翔问题中训练“执行者”网络的算法。TD3算法通过引入双重评价网络、目标策略平滑正则化和延迟更新策略进一步提升了算法的收敛速度和效果。同时, 本文进一步采用“价值扩展”的方式改进了算法更新过程中期望Q值的计算过程, 使得动作网络学习效果更好。
1) 奖励函数设计
本文对于动态滑翔问题的优化目标是单个滑翔周期内最大化能量获取。因此, 强化学习奖励函数设计为
式中，k为大于0的比例系数。当k=1时, r在数值上等于动态滑翔飞行器瞬时总功率。
2) 状态量设计
强化学习中状态量设计为无人机运动学模型(2)中各状态变量
式中, kj>0, j=1, …, 12。将各个状态量转化为数量级相近的变量。
3) 动作值设计
动作值选用动态滑翔简化模型(2)式中的虚拟控制量与控制量作用时间tc的组合
4) 算法流程
算法在“指导者”网络的基础上使用TD3强化学习进行训练, 强化学习网络将输出对于“指导者”网络基准值的偏置, 用于调整其优化策略。执行流程如下。
步骤1 动作现实网络根据无人机动态滑翔训练环境中的状态计算得到一个动作输出, 并与“指导者”网络提供的动作进行叠加, 最终得到动作at并下达给动态滑翔仿真环境执行。
步骤2 动态滑翔仿真环境执行at, 返回奖励rt和新的状态xt+1。
步骤3 将这个状态转换过程(状态xt、动作at、奖励rt和新的状态xt+1)存入经验存储中。
步骤4 从经验存储中采样N个状态转换序列数据, 作为动作网络和评价网络训练的一个小批量数据。
步骤5 利用动作目标网络和评价目标网络计算期望Q值。TD3使用2套评价网络, 从中取最小值后通过“价值扩展”的方式计算期望值，即
式中：Q*表示评价现实网络的期望值, n为价值扩展的步数, C′j表示第j个评价目标网络。A′表示动作目标网络, λA′为动作目标网络的参数, γ是奖励衰减系数, ε~clip(N(0, σ), -c, c), c>0为噪声。“价值扩展”通过考虑未来更多步的奖励值, 因此计算得到的期望值Q将更接近于真实值。评价现实网络的损失函数由(34)式计算。
式中, λjC为第j个评价现实网络的参数。
步骤6 使用Adam优化器根据损失函数的梯度对评价现实网络的参数λjC进行更新。
步骤7 动作现实网络的目标是使评价网络的输出Q值增大, 得到可以获得更多奖励的策略, 所以, 动作现实网络A的梯度通过评价现实网络的梯度计算，如(35)式所示。
式中, J表示损失函数。由(35)式可知, J对λA的梯度由评价现实网络C1对控制输入u的梯度点乘动作现实网络A对其参数λA的梯度得到。
步骤8 采用延迟更新的策略对动作现实网络的参数进行更新, 即评价网络更新多次后, 动作网络才更新一次, 提高动作网络更新的准确性。
步骤9用评价现实网络的参数软更新评价目标网络的参数。即
式中, τ∈(0, 1)是软更新系数。
4 仿真验证
首先使用高斯伪谱算法求解2种经典模式下的动态滑翔问题, 之后进一步引入基于强化学习的“指导者-执行者”机制并进行对比仿真实验。仿真过程中使用到的滑翔机以及环境参数如表 1所示[18]。
滑翔机和环境参数
4.1 高斯伪谱算法求解动态滑翔问题
本小节将使用高斯伪谱算法求解自由行进模式和闭合模式下的动态滑翔问题。无人机状态初值见表 2, 状态量、控制量等参数的最大、最小值限制如表 3所示。
动态滑翔问题无人机状态初值
动态滑翔最优控制问题中参数最大、最小值限制
1) 自由行进模式仿真
自由行进模式下, 高斯伪谱算法优化结果如图 3所示(其中黑线为航迹投影)。由图可知, 高斯伪谱算法优化所得航迹符合动态滑翔的核心机理, 即“逆风爬升, 顺风下滑”。无人机通过重复图 3中单个周期的航迹即可向目标方向前进。无人机从梯度风场中获取的能量功率曲线如图 4所示。由图 4可知, 获取风能的功率呈现2个波峰形状, 恰好对应逆风爬升和顺风下滑2个阶段。除此之外, 图 4中只有横轴上方的阴影, 说明无人机在整个滑翔过程只从风场中获能而没有损失能量。
 |
图3 利用高斯伪谱求解动态滑翔航迹优化结果 |
 |
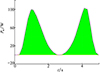图4 无人机从梯度风场中获能功率图 |
2) 闭合模式仿真
闭合模式下, 高斯伪谱算法所得优化三维航迹如图 5所示。由图 5可知, 优化航迹形状类似“8”字, 属于典型的动态滑翔航迹优化结果。无人机先逆风爬升后顺风下滑, 紧接着再一次爬升, 之后下滑到初始位置, 完成周期运动。
 |
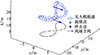图5 高斯伪谱算法在闭合模式下优化航迹三维图 |
3) 考虑障碍物情况下的动态滑翔
考虑多个障碍物情况下的固定翼无人机动态滑翔航迹优化求解中，障碍物用球形包络替代, 2个障碍物球心位置和半径见表 4。
动态滑翔过程中障碍物球心位置和半径
行进方向ε设置为90°, 其中障碍物1刚好处于无人机行进方向上, 因此无人机需要综合考虑躲避障碍和获取能量, 航迹优化结果如图 6所示。由图 6可知, 尽管绿色箭头指向的给定行进方向上存在障碍, 无人机依旧可以优化出1条躲避障碍的航迹, 且终止位置满足行进方向。
 |
图6 考虑障碍物情况下行进模式航迹优化结果 |
4.2 “指导者”网络训练
将由高斯伪谱算法得到的2 000条不同初始值的优化航迹放入航路样本池, 使用(29)式，根据航路样本池中的数据构造训练所用特征向量和标签值。训练过程中均方根误差(RMSE)指标曲线如图 7所示。由图可知, RMSE指标随着训练回合数增加而逐渐减小, 4 000次迭代后逐渐收敛。为评价训练效果, 在相同场景下对比“指导者”神经网络与高斯伪谱算法航迹优化结果, 如图 8所示。“指导者”网络与高斯伪谱算法的优化结果近似。值得注意的是, “指导者”仅为之后的强化学习智能体提供粗略指导, 其本身并不需要完全拟合出一致的策略。
 |
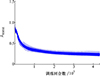图7 神经网络拟合高斯伪谱法策略过程中RMSE变化曲线 |
 |
图8 “指导者”神经网络与高斯伪谱算法航迹优化结果对比 |
4.3 “执行者”网络训练
TD3算法中动作网络为“执行者”, 训练过程中奖励值随训练回合数变化曲线如图 9所示。由图 9可知, 奖励值逐渐增大, 到3 500回合时, 奖励值接近3 000。图 9中红色曲线为滑动平均后的奖励曲线, 从奖励趋势来看智能体相较于最开始时有了明显的策略提升。
 |
图9 强化学习奖励值随训练回合数变化曲线 |
基于强化学习的动态滑翔航迹优化结果如图 10所示。强化学习决策过程中产生的基于“指导者”网络的动作偏置、指导者动作和真实动作随时间变化曲线如图 11所示。由图 11可知, 真实动作由指导者动作加上强化学习动作偏置构成, 智能体通过在合适的时间点对指导者的基础动作进行修正从而更大程度地从环境中获取能量。
 |
图10 基于强化学习的动态滑翔航迹优化结果 |
 |
图11 指导者动作、强化学习输出动作与真实动作曲线 |
4.4 对比仿真
本文所提出的RL方法和传统GP方法在相同场景下动态滑翔平均能量获取功率数据见表 5。
基于强化学习的动态滑翔航迹优化方法和高斯伪谱方法平均能量功率对比
由表 5可知, RL对应的太阳能平均获取功率较GP提升4.8 W, 总能量获取功率略小于GP(3.6 W)。从能量角度而言, RL方法达到了最优结果的88%, 在放弃小部分解最优性的前提下，提升推理速度是可以接受的。
对比本文提出的RL方法和传统GP方法在优化相同动态滑翔问题时的决策耗时, 结果如图 12所示。由图 12可知, RL单次优化平均耗时约0.5 s, 而GP为5.6 s。因此本文提出的基于强化学习的优化算法大大降低了优化时长, 可用于固定翼无人机动态滑翔在线航迹优化。
 |
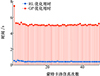图12 RL和GP优化相同动态滑翔问题耗时蒙特卡洛仿真 |
为验证风场变化情况下基于RL的方法有更好的适应性, 在t=2 s时将固定高度风速参考值VR从8 m/s增至10~16 m/s, 风向ew从初始的0°改变至-20°~20°。此时GP方法无法立即应对变化, 只能使用之前离线规划得到的期望航迹进行滑翔, 而RL方法采用单步迭代的计算方式, 可以立即做出变化。风场变化情况下RL和GP方法单个滑翔周期内获取风能如表 6所示。由表 6可知, 随着VR, ew的变化, 基于RL的方法能适应不同的风场强度从而获取更多的风能, 而GP方法面对变化风场时效果不如RL, 获能只有较小幅度提升。
风场变化情况下RL和GP方法单个滑翔周期内获取的风能比较
5 结论
本文针对多能源利用下固定翼无人机动态滑翔航迹优化问题, 借助高斯伪谱法, 提出了一种基于深度强化学习的在线优化方法, 以应对飞行过程中由于风场变化, 导致原有航迹不能充分利用环境能量的问题。仿真结果表明: ①在考虑燃料耗能、飞行阻力耗能、梯度风场获能、太阳能获能、障碍物约束的情况下, 本文提出的算法能有效求解动态滑翔最优航迹; ②“指导者”神经网络可以有效地逼近动态滑翔航迹优化策略, 为后续强化学习训练提供了基础; ③在标准条件下, 传统最优控制算法得到的优化结果与基于强化学习的优化结果在单个滑翔周期相当; ④基于强化学习的动态滑翔航迹优化算法的实时性远优于传统最优控制算法, 航迹解算耗时减少91%;⑤应对变化风场, 基于强化学习的算法具有更好的适应性, 可根据环境情况动态调节策略。
References
- MIR I, EISA S A, TAHA H, et al. A stability perspective of bioinspired unmanned aerial vehicles performing optimal dynamic soaring[J]. Bioinspiration&Biomimetics, 2021, 16(6): 066010 [Google Scholar]
- LIU S, BAI J, WANG C. Energy acquisition of a small solar UAV using dynamic soaring[J]. The Aeronautical Journal, 2021, 125(1283): 60–86 [Google Scholar]
- LIU Duoneng. Research on mechanism and trajectory optimization for dynamic soaring with fixed-wing unmanned aerial vehicles[D]. Changsha: National University of Defense Technology, 2016 (in Chinese) [Google Scholar]
- ZHU Yi, LI Jiguang, HAO Xiangyu. Optimization of dynamic gliding flight trajectory for UAV in gradient wind fields[J]. Journal of Xi'an Aeronautical Institute, 2023, 41(5): 8–16 (in Chinese) [Google Scholar]
- SACHS G P. Maximum travel speed performance of albatrosses and UAVs using dynamic soaring[C]//AIAA Scitech 2019 Forum, 2019: 0568 [Google Scholar]
- MIR I, GUL F, EISA S, et al. On the stability of dynamic soaring: Floquet-based investigation[C]//AIAA Science and Technology Forum and Exposition, 2022: 0882 [Google Scholar]
- ZWENIG A, HONG H, HOLZAPFEL F. Sensitivity analysis of the energy balance of dynamic soaring[J]. Journal of Physics, 2023, 2514(1): 012022 [Google Scholar]
- BOWER G C. Boundary layer dynamic soaring for autonomous aircraft: design and validation[D]. Stanford: Stanford University, 2011 [Google Scholar]
- HONG H, ZHENG H, HOLZAPFEL F, et al. Dynamic soaring in unspecified wind shear: a real-time quadratic-programming approach[C]//2019 27th Mediterranean Conference on Control and Automation, 2019: 600–605 [Google Scholar]
- LAWRANCE N R J, SUKKARIEH S. Autonomous exploration of a wind field with a gliding aircraft[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 719–733 [Google Scholar]
- ARULKUMARAN K, DEISENROTH M P, BRUNDAGE M, et al. A brief survey of deep reinforcement learning[J]. Expert Systems with Applications, 2023, 231: 120495. [Article] [Google Scholar]
- LI Z, LANGELAAN J W. Parameterized trajectory planning for dynamic soaring[C]//AIAA Scitech 2020 Forum, 2020: 0856 [Google Scholar]
- REDDY G, WONGNG J, CELANI A, et al. Glider soaring via reinforcement learning in the field[J]. Nature, 2018, 562(7726): 236–239. [Article] [Google Scholar]
- MONTELLA C. Learning how to soar: steady state autonomous dynamic soaring through reinforcement learning[C]//AIAA Scitech 2020 Forum, 2020: 1848 [Google Scholar]
- LIU S, BAI J, WANG C. Energy acquisition of a small solar UAV using dynamic soaring[J]. The Aeronautical Journal, 2021, 125(1283): 60–86. [Article] [Google Scholar]
- BONNIN V, BÉNARD E, MOSCHETTA J M, et al. Energy-harvesting mechanisms for UAV flight by dynamic soaring[J]. International Journal of Micro Air Vehicles, 2015, 7(3): 213–229. [Article] [Google Scholar]
- FUJIMOTO S, HOOF H, MEGER D. Addressing function approximation error in actor-critic methods[C]//International Conference on Machine Learning, PMLR, 2018: 1587–1596 [Google Scholar]
- LIU Siqi, BAI Junqiang. Analysis of flight energy variation of small solar UAVs using dynamic soaring technology[J]. Journal of Northwestern Polytechnical University, 2020, 38(1): 48–57. [Article] (in Chinese) [Google Scholar]
- BENCATEL R, DE SOUSA J T, GIRARD A. Atmospheric flow field models applicable for aircraft endurance extension[J].Progress in Aerospace Sciences, 2013, 61: 1–25. [Article] [Google Scholar]
- FLANZER T, BUNGE R, KROO I. Efficient six degree of freedom aircraft trajectory optimization with application to dynamic soaring[C]//12th AIAA Aviation Technology, Integration, and Operations Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2012: 5622 [Google Scholar]
- LIU Siqi, BAI Junqiang. Exploration of high-altitude dynamic soaring based on six-degree-of-freedom model[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 703–711 (in Chinese) [Google Scholar]
- MA Dongli, BAO Wenzhuo, QIAO Yuhang. Study of flight path for solar-powered aircraft based on gravity energy reservation[J]. Acta Aeronauticaet Astronautica Sinica, 2014, 35(2): 408–416 (in Chinese) [Google Scholar]
- ZHU Bingjie. Research on mechanism and trajectory optimization for unmanned aerial vehicles by dynamic soaring in gradient wind[D]. Changsha: National University of Defense Technology, 2016 (in Chinese) [Google Scholar]
- MONTELLA C, SPLETZER J R. Reinforcement learning for autonomous dynamic soaring in shear winds[C]//2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2014: 3423–3428 [Google Scholar]
All Tables
All Figures
|
图1 动态滑翔简化模型坐标系及变量之间关系示意图 |
| In the text | |
|
图2 基于深度强化学习的固定翼无人机动态滑翔航迹优化算法框架 |
| In the text | |
|
图3 利用高斯伪谱求解动态滑翔航迹优化结果 |
| In the text | |
|
图4 无人机从梯度风场中获能功率图 |
| In the text | |
|
图5 高斯伪谱算法在闭合模式下优化航迹三维图 |
| In the text | |
|
图6 考虑障碍物情况下行进模式航迹优化结果 |
| In the text | |
|
图7 神经网络拟合高斯伪谱法策略过程中RMSE变化曲线 |
| In the text | |
|
图8 “指导者”神经网络与高斯伪谱算法航迹优化结果对比 |
| In the text | |
|
图9 强化学习奖励值随训练回合数变化曲线 |
| In the text | |
|
图10 基于强化学习的动态滑翔航迹优化结果 |
| In the text | |
|
图11 指导者动作、强化学习输出动作与真实动作曲线 |
| In the text | |
|
图12 RL和GP优化相同动态滑翔问题耗时蒙特卡洛仿真 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.