EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 1 (February 2025) JNWPU, 43 1 (2025) 140-148 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 1, February 2025
Page(s) 140 - 148
DOI https://doi.org/10.1051/jnwpu/20254310140
Published online 18 April 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

红外成像因其独特优势得到越来越广泛的应用, 但红外图像存在对比度低等缺陷, 目标与背景较难区分, 因此有必要对红外图像进行对比度增强等预处理, 以改善图像质量[1]。

直方图均衡(HE)技术因具有较高的实时性, 成为图像增强常用的方法[2]。然而红外图像的背景与目标信息, 在直方图中的数值比例相差较大, 为此研究人员提出了各种直方图改进方案。这些方案通常可以分为2类: 非优化方法和优化方法。

1) 非优化方法: 非优化的方法通常利用经验公式或图像性质对直方图进行校正, 其计算成本低, 易于实现。宋岩峰等[3]提出了双平台直方图均衡(DPHE)算法, 平台阈值仅与图像尺寸有关, 参数的适用性不佳。Liang等[4]提出了一种自适应双平台直方图均衡(ADPHE)算法, 性能相比DPHE算法有所提高, 但其上平台阈值仅由直方图局部峰值点的平均值确定。Lim等[5]提出了基于三平台的双直方图均衡方法(BHE3PL), 该算法不太适用于较暗的红外图像。Lee等[6]提出了基于斜坡的直方图改进算法(SBHE), 该算法对小数据没有处理措施, 因此依然容易出现过度增强现象。Zarie等[7]提出基于标准差的三剪切动态直方图均衡(TCDHE-SD)算法, 将直方图各区间均值作为截断门限。以上非优化算法大多依据经验公式或图像的简单属性, 因此导致此类算法的泛化能力不足。

2) 优化方法: 为了使算法拥有更强的自适应能力以及数学上的严谨性, 研究者引入先验知识或优化模型提出了多种直方图改进的优化方案。Lee等[8]提出了基于斜坡先验的直方图均衡(RDIE)算法。Li等[9]在ADPHE的基础上引入直方图变化的归一化系数(NCVH)来评价对比度增强水平。该算法能避免对比度提升不足, 但不能有效地防止过度增强。Zhang等[10]使用遗传算法(GA)[11]自适应地选择每个子直方图的上下平台阈值, 算法的计算复杂度相对较高。Bhandari等[12]利用樽海群算法(SSA)[13]对每个区间的3个平台阈值进行寻优, 提出了SSA-PL算法。其优化参数的初始值由BHE3PL算法提供, 也不适用于较暗的图像。

由此可见, 大多数算法都采用了平台直方图的思想。但是这些算法都没有对直方图小数据与零数据所采用的平台阈值进行区分, 也没有详细分析各平台阈值之间的关联对图像的影响, 还有一些算法不利于实时处理。此外, 近年来基于非锐化掩模[14]的细节增强方法在红外图像增强领域也比较流行, 例如BF & DDE[15]、GIF & DDE[16]、BEEPS & DDE[17]、ROGABF[18]以及Chen等提出的改进滤波方法[19–20]。这些算法都在基础层利用了平台直方图的思想, 但如何设计最合适的平台阈值, 还未见到较为理想的最优化解决方案。

为了同时满足高性能与实时处理的需求, 本文针对三平台直方图算法, 对各平台值的最优化设计进行研究。首先对第1平台做自适应预处理, 然后在第1与第2平台之间设立约束准则, 并为亮区概率密度为零的灰度级设置第3平台, 而后提出了一种数学优化模型对3个平台值进行整体约束, 旨在保护细节信息的同时尽可能地提高图像的整体对比度。通过该模型最终得到的对比度数值曲线简单直观, 而且计算复杂度较低, 进而说明了约束准则与优化模型的合理性。

1 方法

1.1 三平台直方图的总体方案

前言提到的平台直方图算法缺乏对概率密度为零的灰度级的专业性分析与处理。部分算法对其不做处理, 当直方图右侧的概率密度为零的灰度级个数较多时, 红外图像中的亮目标区域容易出现过度增强。其余算法将直方图中的零数据与小数据提升至同一水平, 此时容易导致对比度提升不足。

所以在双平台算法的基础上, 本文专门为直方图右侧的零数据设置第3平台, 用以控制结果图像的动态范围, 防止亮目标区域的细节信息丢失。算法流程图如图 1所示。

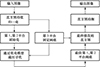thumbnail 图1

算法流程图

本文三平台算法用(1)式描述。

式中：k代表灰度级；μ为图像均值；T1与T2分别为第1平台阈值和第2平台阈值, 由优化模型遍历寻优计算得出。T3为第3平台固定阈值, 专门针对直方图零数据。Pm(k)表示经3个平台阈值修改的直方图, 如图 2中红色线所示。p(k)为均值归一化之后的直方图, 如图 2中黑色线所示。p(k)被定义为

thumbnail 图2

三平台直方图示意图

式中：h(k)为原始直方图；N为图像总像素数；L为图像的动态范围, 对于8 bit图像，L为256, 对于16 bit图像，L为65 536。直方图h(k)被均值归一化处理后, 新直方图数组p(k)的均值为1。

对被3个平台阈值修改过后的新直方图Pm(k)执行均衡操作, 均衡的公式为

式中，SLUT(k)为映射查找表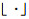；表示向下取整。R为结果图像的动态范围, 默认等于L。

后续小节分析各平台阈值的作用以及各平台之间的关联, 并讨论如何求取最优的三平台值。

1.2 各平台阈值的设计与分析

1.2.1 第1平台自适应预处理

第1平台对增强效果起着主要作用, 第1平台取值过大容易导致背景区域过度增强。因此在确定其最优值前, 有必要先限定T1的取值范围, 定义其最大可能取值为Tmax。对于不同类型的红外图像, 应考虑自适应地设置Tmax。

当直方图中概率密度为零的灰度级个数较多时, 直方图容易过度展开, 如图 3b)所示, 该直方图只有50%的非零灰度级个数, 此时Tmax应当设置较小以避免图像过度增强。另外, 当图像照度很低或很高时, 直方图呈现显著的峰值, 如图 3d)所示。为了使低暗区或高亮区的图像对比度提高, 此时Tmax应当设置较大。根据以上分析, 8 bit红外图像的Tmax计算公式为

thumbnail 图3

Tmax取值示意图

式中：pmax为经过均值归一化后的直方图的峰值, 注意Tmax为最大直方图峰值; c为经验值常数, 取值在pmax左右, 实验发现大多数红外图像的pmax不超过25, 如图 3所示。本文c取值为20, c可参照直方图峰值大小进行调整。α表示直方图中非零灰度级总数与图像动态范围L的比值; μ为图像归一化的均值。如图 3d)所示, 它的为0.081, 1- μ的设置可以防止图像均值过小导致Tmax过小的情况。

当通过(4)式确定Tmax之后, 最优的T1值便从(0, Tmax]中产生。假设先使用Tmax对直方图钳位

后续讨论如何在(0, Tmax]范围内计算最优的T1值。

1.2.2 第1与第2平台间的约束准则

在增强对比度时, 仅靠1个平台很难对细节信息起到保护作用, 因此有必要设置第2平台。

现有算法没有详细分析平台值之间的关联对图像的影响。根据实验观察, 在红外图像直方图中, 亮目标所处的灰度级较高, 但通常概率密度较小, 当T1变化时, 亮目标区域容易被具有大概率密度的背景像素影响。随着T1的增大, 亮目标信息得到保护的力度也应当增大, 否则亮目标区域可能出现亮度异常和对比度异常。因此设定第1与第2平台间的约束准则为: 第2平台与第1平台呈正相关的约束关系。

此外, 当小概率对应的“亮”灰度级总数越多, 说明亮目标区域的细节越丰富, 因此T2也应当与细节的丰富程度呈正比，即

式中，Wr表示直方图中灰度级大于μ且概率密度较小的非零灰度级总数与所有非零灰度级个数的比值。Wr可用(9)式定义，Wr越大, T2越大, 亮目标得到保护的力度越大。

实验发现, 相比亮度正常的图像, 暗红外图像的Wr相对较大。为了防止T2被提升太多导致图像对比度提升不足, 另外增加图像的均值作为校正参数。最终T2与T1的定量关系为

式中，γ作为校正参数被引入，防止过小的情况, γ在本文中取值为0.65。

1.2.3 第3平台的设计思想

虽然现有研究中也曾出现三平台思想, 比如BHE3PL、SSA-PL、TCDHE-SD算法, 但它们都没有对零数据进行处理。当直方图中概率密度为零的灰度级很多时, 这些算法的结果图像的动态范围不可控。

本文专门设置第3平台对直方图右侧的零数据进行提升, 实验发现, T3与概率密度为零的灰度级总数正相关, 同时与图像均值正相关。T3被定义为

式中，β为常数, 取值在1~3之间, β越大意味着结果图像的动态范围越受限。以图 4为例, β为0时等同于没有第3平台, 从图 4b)可以看出屋顶区域产生明显的过曝现象, 图 4e)中直方图的动态范围达到最大。β为2时, 结果图像及其直方图分别如图 4c)与图 4f)所示。图 4c)没有过曝, 而且从图 4f)中可以看出最高灰度级没有达到255, 因此第3平台的设置可以使结果图像的动态范围得到控制。

thumbnail 图4

不同β值对应的结果图像及其直方图

W0表示直方图中像素值大于μ且概率密度为零的灰度级个数占比, W0越大, T3的值越大。W0定义为

1.3 以对比度为评估参数的优化模型

根据以上分析, 在确定T3, Tmax以及T1与T2之间的正相关约束准则后, 开始计算最优的T1值。

首先借助直方图从理论上分析。假设T1从小到大变化, 初始阶段各平台阈值都很小, 均衡后结果图像的对比度较小。在变化过程中, T2与T1呈正相关关系, T1增加的步长相对较大, 因此T1先起主要作用。随着T1的增大, 结果图像的对比度逐渐增大, 同时T2也逐渐增大。虽然T2增加的步长相对较小, 但概率密度得到提升的灰度级数量越来越多, 对T1的对冲与限制作用也越来越强。当到达一定程度后, T2将会起主要作用, 使均衡后结果图像的对比度呈现减小的趋势, 最大对比度将在某个最优参数时获得。

根据以上分析, 本文提出一种以对比度为评估参数的数学优化模型

式中，pout(T1, T2, T3)表示经三平台直方图均衡后结果图像的概率密度直方图, 可以利用从(3)式得到的SLUT计算, 加速求解过程; C(p)为Wu[21]提出的对比度定义方式, 比较精确灵敏, 能够很好地反映直方图微小的间隔变化。

式中：xi表示概率密度直方图p中的第i个非零灰度级；pi表示xi对应的概率密度；K为非零灰度级的总数。

对于此最优化问题的求解, 本文采用遍历的方式对T1进行寻优。在遍历过程中T1的取值为

Tmax表示T1能遍历到的最大值, n代表遍历次数, 本文取值为30~50, 即本文算法需要进行30~50次遍历。当得到最优的T1后, T2根据正相关关系计算得出。

图 5显示了2幅典型图像的优化曲线, 从图 5可以看出, 与之前的理论分析一致, 图像的对比度数值呈现先上升后下降的趋势, 并且曲线接近比较完美的凸形。图 5中红色点对应的T1值即为最佳的T1值。具体过程如伪代码所示。

thumbnail 图5

对比度曲线示意图

本文算法流程描述:

输入: 原始红外图像X

输出: 增强图像Xout

1. 确认图像动态范围L, 计算直方图h(k)

2. 根据(2)式将直方图均值归一化得到p(k)

3. 计算μ和μ, 根据(9)式计算Wr, 根据(14)式计算W0, 根据(13)式计算T3

4. 根据(4)式计算Tmax

5. For T1=T3: t: Tmax do

6. 根据(12)式计算T2

7. 将T1, T2, T3代入(1)式对直方图修改并通过(3)式得到SLUT

8. 通过SLUT计算pout, 将pout代入(17)式中计算对应的C(p), 保存C(p)的值

9. End For

10. 找出最大的C(p)及其对应的T1, 根据(12)式计算T2

11. 通过T1, T2, T3对直方图修改并均衡得到最终的增强图像Xout。

2 实验结果

在本节中选取3个公开数据库中的红外图像来评估增强算法。图 6a)和图 7a)为从Dataset 1[22]和Dataset 2[23]下载的8 bit红外图像, 分辨率分别为384×288和640×480。图 8a)是从Dataset 3[24]下载的16 bit图像, 分辨率为512×512。选取6种现有的平台直方图相关算法作为对比算法, 即ADPHE, NCVH, SBHE, RDIE, TCDHE-SD, SSA-PL算法。

thumbnail 图6

场景1的增强结果图像

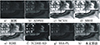thumbnail 图7

场景2的增强结果图像

thumbnail 图8

场景3的增强结果图像

2.1 主观评价

场景1和场景2是8 bit红外图像, 从图 6和图 7对应的增强结果中可以看出, ADPHE算法对于某些场景的自适应能力不足。NCVH及SBHE算法容易产生过度增强现象。TCDHE-SD算法容易将亮目标区域提升得过亮。SSA-PL算法由于亮度保持容易导致图像对比度提升不足。相比RDIE算法, 本文算法的增强结果更自然, 局部增强效果更明显。

场景3是一幅16 bit红外图像, 由于16 bit红外图像的直方图数据与8 bit图像相差较大, 为了尽可能提高图像的对比度, 16 bit图像的Tmax可以定义为直方图峰值。增强结果如图 8所示, ADPHE, NCVH, SBHE算法对于背景与人之间的对比度增强效果不明显。SSA-PL算法的结果与原图类似。TCDHE-SD算法增强了背景与人之间的对比度, 但是地面区域的细节不明显。RDIE算法与本文算法效果类似, 相比之下, 本文算法更好地显示了地砖的纹理细节, 书包与衣服之间的局部对比度更强。

此外, 为了进一步验证算法对多种红外场景的普适性, 本文又从数据库中选取8幅典型红外图像进行测试, 包括室外城市场景、室外树林场景、室内场景、夜间场景等, 其中夜间场景图像来自网址 https://projects.asl.ethz.ch/datasets/doku.php?id=ir:iricra2014。增强结果如图 9所示。

thumbnail 图9

典型红外场景的增强结果图像

本文算法能够较好地提高图像对比度, 并且能够较好地保护亮目标区域的信息。经过实验观察与分析, 本文算法可以处理较多种红外目标与场景, 尤其对于主要灰度级分布较为集中的红外图像具有较好的效果。

2.2 客观评价

本节采用3种不同的度量方式, 对各算法的增强结果进行客观评价。各度量方式的定义如下。

1) 离散熵(DE)[25]代表了图像所含细节的丰富程度, 理论上DE越大越好, DE被定义为

式中：O代表增强后的图像；p(s)代表灰度级s对应的概率密度。定义p(s)为0时, ηDE值为0。

2) 线性模糊指数γ[26]越小表示目标与背景之间的对比度越大, 被广泛地应用于评价红外图像

式中：M与N是图像的宽和高；q(i, j)被定义为

3) 自然图像评价指标NIQE[27]越小, 表示图像的自然程度越高, 越符合人眼主观感受。

式中，v1, v2, 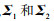分别为自然图像和失真图像的多变量高斯模型的均值和协方差矩阵。

表 1列出了上述3个指标在图 6~8(即场景1~3)上的评价结果, 粗体值和带下划线的值分别表示最优和次优结果。从表 1可以看出, 本文算法的ηDE值位于第1位, γ值和λNIQE值基本位于前2位。

表1

不同算法增强后图像的客观指标

为了验证客观结果的准确性, 在每个数据库中随机选择300张图像测试, 表 2展示了平均度量结果, 表中粗体值和带下划线的值分别表示最优和次优结果，本文算法的客观指标结果基本排在前3位。

表2

各指标在数据集上的平均值

此外, 还计算了各算法在图 6~8上的运行时间, 测试平台是1台配备Intel i7-6700处理器和8 GB RAM的MATLAB R2020a版本的计算机。从表 3可以看出, SSA-PL算法因需要多次迭代，运算速度最慢。本文算法仅需循环30~50次, 并且是对直方图数据进行处理, 计算复杂度大大降低。在处理16 bit图像时, 由于需要通过直方图间距计算对比度大小, 16 bit图像灰度级个数较多, 所以运行时间相对较长。但在处理8 bit图像时, 本文算法的运行时间约为0.02 s, 具有较高的实时应用价值。

表3

不同算法的运行时间

3 结论

本文针对三平台直方图算法, 提出了一种以对比度为评估参数的优化模型, 首先对第1平台自适应预处理, 其次为第1与第2平台之间设立正相关约束准则, 然后为亮区零概率的灰度级设置第3平台, 最后在约束准则下通过优化模型对3个平台值进行整体约束。在多个数据库上的实验结果表明, 本文算法具有较好的主观视觉效果与客观指标, 同时具有较高的实时性。本文算法采用顺序搜索方式, 对比度变化比较有规律, 数值曲线简单直观, 也可采用GA等基于随机搜索的优化算法。

此外, 本文算法也具有较好的可扩展性, 该优化模型的思想也可用于基于分块的HE算法中, 为每个图像块寻找最佳平台阈值, 从而达到整体更优的效果。另外, 如果将第3平台应用在直方图所有的非零灰度级上, 则本文的三平台方法也可以应用于可见光图像的增强处理。

References

  1. SOUNDRAPANDIYAN R, SATAPATHY S C, et al. A comprehensive survey on image enhancement techniques with special emphasis on infrared images[J]. Multimedia Tools and Applications, 2022, 81(7): 9045–9077. [Article] [Google Scholar]
  2. JÄHNE B. Digital image processing[M]. Cham: Springer Science&Business Media, 2005 [Google Scholar]
  3. SONG Yanfeng, SHAO Xiaopeng, XU Jun. New enhancement algorithm for infrared image based on double plateaus histogram[J]. Infrared and Laser Engineering, 2008(2): 308–311. [Article] (in Chinese) [Google Scholar]
  4. LIANG K, MA Y, XIE Y, et al. A new adaptive contrast enhancement algorithm for infrared images based on double plateaus histogram equalization[J]. Infrared Physics&Technology, 2012, 55(4): 309–315 [Google Scholar]
  5. LIM S H, MAT ISA N A, OOI C H, et al. A new histogram equalization method for digital image enhancement and brightness preservation[J]. Signal, Image and Video Processing, 2015, 9(3): 675–689. [Article] [Google Scholar]
  6. LEE S, KIM D, KIM C. Slope-based histogram equalization for real-time display of high-quality infrared imagery[C]//2018 IEEE International Conference on Consumer Electronics, 2018: 206–212 [Google Scholar]
  7. ZARIE M, PARSAYAN A, HAJGHASSEM H. Image contrast enhancement using triple clipped dynamic histogram equalisation based on standard deviation[J]. IET Image Processing, 2019, 13(7): 1081–1089. [Article] [Google Scholar]
  8. LEE S, KIM D, KIM C. Ramp distribution-based image enhancement techniques for infrared images[J]. IEEE Signal Process-ing Letters, 2018, 25(7): 931–935. [Article] [Google Scholar]
  9. LI S, JIN W, LI L, et al. An improved contrast enhancement algorithm for infrared images based on adaptive double plateaus histogram equalization[J]. Infrared Physics&Technology, 2018, 90: 164–174 [Google Scholar]
  10. ZHANG H, QIAN W, WAN M, et al. Infrared image enhancement algorithm using local entropy mapping histogram adaptive segmentation[J]. Infrared Physics&Technology, 2022, 120: 104000 [Google Scholar]
  11. JONES G, WILLETT P, GLEN R C, et al. Development and validation of a genetic algorithm for flexible docking[J]. Journal of Molecular Biology, 1997, 267(3): 727–748. [Article] [Google Scholar]
  12. BHANDARI A K, KANDHWAY P, MAURYA S. Salp swarm algorithm-based optimally weighted histogram framework for image enhancement[J]. IEEE Trans on Instrumentation and Measurement, 2020, 69(9): 6807–6815. [Article] [Google Scholar]
  13. MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163–191. [Article] [Google Scholar]
  14. HUANG J, MA Y, ZHANG Y, et al. Infrared image enhancement algorithm based on adaptive histogram segmentation[J]. Applied Optics, 2017, 56(35): 9686. [Article] [Google Scholar]
  15. ZUO C, CHEN Q, LIU N, et al. Display and detail enhancement for high-dynamic-range infrared images[J]. Optical Engineering, 2011, 50(12): 1 [Google Scholar]
  16. LIU N, ZHAO D. Detail enhancement for high-dynamic-range infrared images based on guided image filter[J]. Infrared Physics&Technology, 2014, 67: 138–147 [Google Scholar]
  17. LI Y, LIU N, XU J, et al. Detail enhancement of infrared image based on bi-exponential edge preserving smoother[J]. Optik, 2019, 199: 163300. [Article] [Google Scholar]
  18. FENG X, PAN Z. Detail enhancement for infrared images based on relativity of Gaussian-adaptive bilateral filter[J]. OSA Continuum, 2021, 4(10): 2671. [Article] [Google Scholar]
  19. CHEN Y, KANG J U, ZHANG G, et al. Real-time infrared image detail enhancement based on fast guided image filter and plateau equalization[J]. Applied Optics, 2020, 59(21): 6407. [Article] [Google Scholar]
  20. LYU H, SHAN P, SHI H, et al. An adaptive bilateral filtering method based on improved convolution kernel used for infrared image enhancement[J]. Signal, Image and Video Processing, 2022, 16(8): 2231–2237 [Google Scholar]
  21. WU Xiaolin. A linear programming approach for optimal contrast-tone mapping[J]. IEEE Trans on Image Processing, 2011, 20(5): 1262–1272 [Google Scholar]
  22. MORRIS N J W, AVIDAN S, MATUSIK W, et al. Statistics of infrared images[C]//2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1–7 [Google Scholar]
  23. BERG A, AHLBERG J, FELSBERG M. A thermal object tracking benchmark[C]//2015 12th IEEE International Conference on Advanced Video and Signal Based Surveillance, 2015: 1–6 [Google Scholar]
  24. WU Z, FULLER N, THERIAULT D, et al. A thermal infrared video benchmark for visual analysis[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2014: 201–208 [Google Scholar]
  25. SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(3): 379–423. [Article] [CrossRef] [Google Scholar]
  26. LAI R, YANG Y, WANG B, et al. A quantitative measure based infrared image enhancement algorithm using plateau histogram[J]. Optics Communications, 2010, 283(21): 4283–4288 [Google Scholar]
  27. MITTAL A, SOUNDARARAJAN R, BOVIK A C. Making a "completely blind" image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209–212 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

表1

不同算法增强后图像的客观指标

In the text
表2

各指标在数据集上的平均值

In the text
表3

不同算法的运行时间

In the text

All Figures

thumbnail 图1

算法流程图
In the text
thumbnail 图2

三平台直方图示意图
In the text
thumbnail 图3

Tmax取值示意图
In the text
thumbnail 图4

不同β值对应的结果图像及其直方图
In the text
thumbnail 图5

对比度曲线示意图
In the text
thumbnail 图6

场景1的增强结果图像
In the text
thumbnail 图7

场景2的增强结果图像
In the text
thumbnail 图8

场景3的增强结果图像
In the text
thumbnail 图9

典型红外场景的增强结果图像
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.