A turbulence reduced order model based on non-interpolated convolutional autoencoder

Pin WU; Bo ZHANG; Chao SONG; Zhu ZHOU

doi:10.1051/jnwpu/20254310149

All issues

Volume 43 / No 1 (February 2025)

JNWPU, 43 1 (2025) 149-153

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 1, February 2025


Page(s)		149 - 153
DOI		https://doi.org/10.1051/jnwpu/20254310149
Published online		18 April 2025

JNWPU 2025, 43(1): 149–153

A turbulence reduced order model based on non-interpolated convolutional autoencoder

基于非插值卷积自编码器的湍流降阶模型

Pin WU (武频)¹, Bo ZHANG (张波)¹^,2, Chao SONG (宋超)³ and Zhu ZHOU (周铸)³

¹ School of Computer Engineering and Science, Shanghai University, Shanghai 200444, China
² Institute of Artificial Intelligence, Shanghai University, Shanghai 200444, China
³ Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China

Received: 7 December 2023

Abstract

Reduced-order modeling stands as a pivotal method in curbing the computational expenses linked with expansive fluid dynamics quandaries by employing proxy numerical simulations. Within this realm, downscaling and reconstruction methods serve as fundamental constituents of reduced-order modeling. The traditional intrinsic orthogonal decomposition relies on linear mapping, often relinquishing a substantial amount of nonlinear flow information within the flow field. Meanwhile, autoencoders equipped with fully-connected structures, maybe encounter a parameter explosion when handling larger-scale flow field meshes, impeding effective training. Convolutional autoencoders necessitate uniform interpolation across the flow field to attain a uniform flow field snapshot, yet this process frequently introduces interpolation errors and unwarranted temporal overheads. This paper introduces an innovative solution: a non-interpolated convolutional autoencoder, designed to extract nonlinear features from the flow field while curbing parameter count, evading interpolation errors, and mitigating additional computational burdens. Illustratively, in a two-dimensional cylindrical winding flow scenario, both the reduced dimensional reconstruction display root mean square errors of approximately 1×10^-3. Notably, the velocity cloud and absolute error cloud vividly exhibit the non-interpolated convolutional autoencoder's remarkable prowess in reconstruction.

摘要

降阶模型通过代理数值模拟, 有效降低了大规模流体动力学问题的计算成本。其中, 降维和重构方法是降阶模型的关键组成部分。传统的本征正交分解基于线性映射, 常常在处理流场时损失大量非线性流动信息。全连接结构的自编码器在处理较大规模流场网格时会导致模型参数爆炸, 难以有效训练。为了获得均匀流场快照, 卷积自编码器一般需要在流场上进行均匀插值, 这通常伴随着插值误差和不必要的时间成本。为解决这些问题, 提出了一种创新的非插值卷积自编码器, 该模型可以提取流场的非线性特征, 降低参数量, 避免插值误差和额外的计算成本。在二维圆柱绕流算例上, 降维重构的均方根误差均约为1×10^-3, 速度云图和绝对误差云图展示了非插值卷积自编码器在重构方面的卓越性能。

Key words: reduced-order model / non-interpolated convolutional autoencoder / reduced-dimensional reconstruction

关键字 : 降阶模型 / 非插值卷积自编码器 / 降维重构

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

数据驱动的降价模型(reduced-order model, ROM)广泛应用于复杂流场分析, 在保留原流场主要流动特性的前提下, 使用特征提取的方法将高维流场数据压缩成低维数据, 这大大降低了流场的复杂度和计算量[1–2]。传统的ROM其实是对复杂非线性系统的线性近似, 例如本征正交分解(proper orthogonal decomposition, POD)和动态模式分解(dynamic mode decomposition, DMD)等方法。POD方法可以提取在动态系统中占大部分能量的特征向量, 因此被广泛应用于各种工程问题[3–4]。POD方法的变体POD-Galerkin是对POD线性投影的改进, 通过将高维系统投影到一个低维子空间并加以物理条件约束, 得到更准确的低维表征。郭子漪等[5]构建了不同体积比下, 二维有限长液层热毛细对流的POD-Galerkin低维模型, 验证了利用POD-Galerkin降维方法研究热毛细对流的可行性。DMD与POD一样, 是一种模态分解法。更准确地说, DMD是一种时空耦合的模态分解方法, 其分解后的模态具有单一的频率和增长率, 便于对流场流动模式的分析。Zhang等[6]结合了深度神经网络和DMD算法, 提出了一种新的压缩感知降阶模型框架来预测非定常流。Schmid[7]介绍了DMD及其变体的具体方法, 以及它在分析复杂流体过程中的用途和特征。尽管这些模型能够捕获流场的主要流动模式, 但由于其线性假设, 对于复杂的强非线性流动系统, 容易失去其物理特性, 导致建模精度下降。

随着深度学习和计算设备的快速发展, 为了简化计算量和降低复杂度, 将人工智能应用于建立基于CFD数值模拟的流场近似模型成为了一个热门的研究课题[8]。其中, 基于自编码器(autoencoder, AE)的非线性降阶模型技术发展十分迅速。Simpson等[9]使用AE和长短期记忆网络(long short-term memory, LSTM)创建系统的非线性降阶模型, 能够在已知数据输入的情况下重建整个系统的动态响应。Franco等[10]在参数相关偏微分方程(partial differential equations, PDE)的框架内, 开发了一种基于深度自编码器的构造方法, 用于参数到解映射的有效近似。耦合自注意力机制的卷积自编码器(convolutional autoencoder, CAE)[11]是对CNN的深度利用, 通过多层卷积和自注意力操作将感受野传递、提升并可以不断缩小特征尺寸, 最终少量神经元就能够包含所有的特征信息。然而, 由于二维、三维卷积的特性, CAE模型一般需要做插值前处理, 将快照变成均匀像素点, 这会带来插值误差并增加插值时间成本。

本文提出了一种创新的非插值卷积自编码器(non interpolation convolutional autoencoder, NICAE)。该模型采用尺寸为13的一维大卷积核和膨胀卷积, 以扩大物理感受域, 实现对瞬时高维复杂系统特征信息的高精度、多尺度提取, 通过引入LeakyReLu激活函数增加非线性。NICAE逐步将高维系统转换至低维系统, 既能有效提取流场的非线性特征, 又能降低参数量、避免插值误差和减少插值成本。在二维圆柱绕流算例中, NICAE在降维重构阶段的平均均方根误差(root mean square error, RMSE)约为1.0×10^-3。

1 方法

在本节中, 将详细介绍本文提出的NICAE模型。

本文所提出的NICAE模型在降维和重构方面进行了创新, 特别是解决了CAE模型中需要进行插值的问题, 从而避免了繁琐的插值步骤和插值误差。

NICAE模型由编码器和解码器组成, 详细结构如图 1所示, 它们都由N个编码模块和解码模块堆叠而成, 每个编码模块和解码模块在整个模型中都呈对称排列。编码器的主干采用一维卷积神经网络, 其中卷积核大小为13, 膨胀率为o。一维卷积通过对卷积窗口的数据执行点积运算, 以提取局部特征。其平移不变性的特点使得在某一位置学到的特征能够在其他位置识别, 并且与二维和三维卷积不同, 不需要数据点均匀分布(通常128×128或256×256被视为图片处理的标准)。因此, 无需因为网格疏密度的不同而进行繁琐的插值处理, 从而大幅减少数据准备工作的复杂性, 避免插值误差。

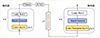图1

NICAE模型的详细结构图

此外, 本文选用均方误差(mean square error, MSE)作为模型的损失函数, 以评估流场重构快照与流场高保真快照之间的接近程度。在最小化均方误差的过程中, 每次训练的输出误差会通过解码器反向传播到编码器, 将误差分摊至各层所有单元。这样一来, 能够获得各层单元的误差信号, 从而有效修正各单元的权值。这种反向传播机制不仅有助于提高模型对流场特征描述的准确性, 还确保了模型的训练过程是基于实际重构结果与真实快照之间的一致性, 从而优化整个降阶模型的性能, 计算公式为

式中：D为流场快照的规模; x_i是流场的离散值; 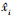是模型重构值。

2 实验

在本节中将详细介绍实验的设置, 包括实验环境、实验用例以及对比方法等。随后, 将呈现实验结果并进行深入分析。

2.1 实验设置

2.1.1 实验环境

本文的实验采用以下计算机设备: 英特尔E5 2678V3处理器, 搭配4张英伟达RTX 3090显卡。使用Conda虚拟环境, 其中Python版本为3.9.7, PyTorch版本为1.11.0, CUDAToolkit版本为11.3.1。

2.1.2 二维圆柱绕流

本研究以经典的二维圆柱绕流案例为例, 验证了所提出的NICAE性能。计算域的示意图和网格构建见图 2。图 2a)中圆柱绕流矩形计算域长为0.2 m, 宽为0.1 m, 图 2b)是流场网格。流体入口位于左侧, 流体出口位于右侧, 而中间则设有半径为0.01 m的圆柱。通过CFD数值模拟软件获得了流场的高保真数值解, 并从中选取了2 000个时间步的高精度快照, 作为模型的训练集和测试集(比例为7∶3)。在湍流瞬时状态下, 每个时间步的时间间隔设为Δt=0.005 s, 流过流场的流体为空气, 密度ρ=1 kg/m³, 黏度μ=2×10^-5 kg/(m·s), 流体速度v=1 m/s, 雷诺数Re=1 000, y⁺=1。在二维圆柱绕流达到动态稳定后, 形成的卡门涡街表现出强烈的非线性, 充分展示了本文模型提取非线性流场流动模式的能力。

图2

二维圆柱绕流流场计算域和流场网格示意图

2.1.3 评价标准

为了全面评价模型性能, 本文采用了3种评价指标: 均方根误差、重构云图以及绝对值误差云图(absolute error, AE)。均方根误差是m次观测值与真值偏差的平方和与观测次数m比值的平方根。该指标对1组测量中的特大或特小误差非常敏感, 因此能够有效反映测量的精密度。一般而言, 均方根误差越小, 表示模型的精度越高, 性能越出色。均方根误差的计算公式为

重构或预测云图是一种可视化结果, 通过直观观察可以感受模型是否准确地还原了流场的流动特征。

2.2 实验结果

从图 3可以观察到, 在测试集的第1 401步至第2 000步的流场快照中, NICAE模型每个时间步的重构均方根误差均小于POD。其中, 最大误差约为1.4×10^-3, 最小误差约为5×10^-4。这表明本文提出的NICAE模型在重构精度方面优于POD降维方法, 并且表现相对稳定。图 4中的速度云图直观展示了NICAE模型和POD方法在第1 401步和第1 650步的快照重构效果, 白色为障碍物圆柱, 其他颜色表示流体的不同速度。重点观察和比较速度云图中的3个部分: 缓流区、尾流区、涡旋结构。缓流区是在圆柱顶部和底部形成的流速较低的区域, 这是气流在圆柱表面分离产生涡旋的结果, 可以通过观察该区域了解流体分离和绕流现象。

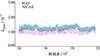图3

NICAE模型与POD方法在测试集1 401~ 2 000步的流场快照重构均方根误差

图 4中缓流区即为圆柱上下的蓝色区域, 2种方法都准确重构了缓流区的形态和细节, 进一步观察两者重构速度云图和高保真速度云图的绝对误差云图(见图 5)。

图4

高保真(high fidelity)与POD、NICAE重构在测试集第1 401步和第1 650步的速度云图

图5

POD、NICAE在第1 401步和第1 650步的重构误差云图

通过观察图 5的误差云图可见, POD的重构误差几乎全部集中在具有较强非线性流动规律的圆柱尾流区域和圆柱上下的缓流区, 这些区域是观察流场规律和流动现象的重要区域。POD线性映射导致在流场的重要区域损失大部分非线性流动信息, 包括涡旋结构、壁面受阻效应, 而这些信息通常是观察流场和推演流场的关键。相比之下, NICAE的重构误差在整个流场中分布较为均匀且数值很小, 缓流区误差几乎没有, 尾流区域存在一些明显的重构误差, 但总体来看数量少, 且数值小于POD, 表明NICAE有着更好的流场降维重构效果。NICAE的主要目标是捕获流场的关键非线性流动特征, 通过22个LeakyReLU激活函数将流场非线性映射至低维隐空间, 对于几乎没有非线性流动的区域可能存在一些映射误差, 然而这些区域并非观察的关键区域且误差数值较小。

3 结论

本文提出了一种创新性的非插值卷积自编码器模型, 采用尺寸为13的一维大卷积核和膨胀卷积来扩大物理感知域, 将高维流场转化为多通道一维非线性场域的堆叠。通过池化和全连接操作逐步降低数据维度, 最终得到包含完整流场信息的低维表征。NICAE模型构建于本研究组的前期工作之上, 成功克服了多层自编码器无法处理超大规模网格的限制以及卷积自编码器在处理中需进行繁琐插值的问题。本文在二维圆柱绕流算例上进行模型验证, NICAE在降维重构阶段的平均RMSE约为1.0×10^-3明显优于传统的POD方法。

尽管如此, 随着网格规模增至百万、千万甚至亿级别, NICAE模型的网格深度也需相应增加, 这对训练过程提出了更高的要求, 可能导致计算资源的进一步消耗。另外, 神经网络作为一种黑盒模型, 其内在机制难以解释, 这在一些应用场景中可能限制了其可信度和可用性。因此, 迫切需要研究如何在保持高性能的同时, 降低NICAE模型的训练复杂性, 并在一定程度上增强其可解释性。未来的研究方向包括优化网络架构、探索有效的正则化方法以及开发可解释性强的模型解释技术, 以促进NICAE模型在大规模网格环境中的可持续发展。

References

GONCALVES E, HOUDEVILLE R. Turbulence model and numerical scheme assessment for buffet computations[J]. International Journal for Numerical Methods in Fluids, 2004, 46(11): 1127–1152 [Google Scholar]
CHEN G, LI D, ZHOU Q, et al. Efficient aeroelastic reduced order model with global structural modifications[J]. Aerospace Science and Technology, 2018, 76: 1–13 [Google Scholar]
KERSCHEN G, GOLINVAL J C, VAKAKIS A F, et al. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview[J]. Nonlinear Dynamics, 2005, 41(1/2/3): 147–169 [Google Scholar]
FRESCA S, MANZONI A. POD-DL-ROM: enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 388: 114181. [Article] [Google Scholar]
GUO Ziyi, ZHAO Jianfu, LI Kai, et al. Bifurcation analysis of thermocapillary convection based on POD-Galerkin reduced-order method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(5): 1186–1198 (in Chinese) [Google Scholar]
ZHANG X, JI T, XIE F. Unsteady flow prediction from sparse measurements by compressed sensing reduced order modeling[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114800 [Google Scholar]
SCHMID P J. Dynamic mode decomposition and its variants[J]. Annual Review of Fluid Mechanics, 2022, 54(1): 225–254. [Article] [Google Scholar]
SCHILDERS W H A, VORST H A V D, ROMMES J. Model order reduction: theory, research aspects and applications[M]. Berlin: Springer, 2008 [CrossRef] [Google Scholar]
SIMPSON T, DERVILIS N, CHATZI E. Machine learning approach to model order reduction of nonlinear systems via autoencoder and LSTM Networks[J]. Journal of Engineering Mechanics, 2021, 147(10): 04021061 [Google Scholar]
FRANCO N, MANZONI A, ZUNINO P. A deep learning approach to reduced order modelling of parameter dependent partial differential equations[J]. Mathematics of Computation, 2022, 92(340): 483–524 [Google Scholar]
WU P, GONG S, PAN K, et al. Reduced order model using convolutional auto-encoder with self-attention[J]. Physics of Fluids, 2021, 33(7): 077107 [Google Scholar]

All Figures

	图1 NICAE模型的详细结构图
In the text

	图2 二维圆柱绕流流场计算域和流场网格示意图
In the text

	图3 NICAE模型与POD方法在测试集1 401~ 2 000步的流场快照重构均方根误差
In the text

	图4 高保真(high fidelity)与POD、NICAE重构在测试集第1 401步和第1 650步的速度云图
In the text

	图5 POD、NICAE在第1 401步和第1 650步的重构误差云图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] GONCALVES E, HOUDEVILLE R. Turbulence model and numerical scheme assessment for buffet computations[J]. International Journal for Numerical Methods in Fluids, 2004, 46(11): 1127–1152 [Google Scholar]

[2] CHEN G, LI D, ZHOU Q, et al. Efficient aeroelastic reduced order model with global structural modifications[J]. Aerospace Science and Technology, 2018, 76: 1–13 [Google Scholar]

[3] KERSCHEN G, GOLINVAL J C, VAKAKIS A F, et al. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview[J]. Nonlinear Dynamics, 2005, 41(1/2/3): 147–169 [Google Scholar]

[4] FRESCA S, MANZONI A. POD-DL-ROM: enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 388: 114181. [Article] [Google Scholar]

[5] GUO Ziyi, ZHAO Jianfu, LI Kai, et al. Bifurcation analysis of thermocapillary convection based on POD-Galerkin reduced-order method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(5): 1186–1198 (in Chinese) [Google Scholar]

[6] ZHANG X, JI T, XIE F. Unsteady flow prediction from sparse measurements by compressed sensing reduced order modeling[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114800 [Google Scholar]

[7] SCHMID P J. Dynamic mode decomposition and its variants[J]. Annual Review of Fluid Mechanics, 2022, 54(1): 225–254. [Article] [Google Scholar]

[8] SCHILDERS W H A, VORST H A V D, ROMMES J. Model order reduction: theory, research aspects and applications[M]. Berlin: Springer, 2008 [CrossRef] [Google Scholar]

[9] SIMPSON T, DERVILIS N, CHATZI E. Machine learning approach to model order reduction of nonlinear systems via autoencoder and LSTM Networks[J]. Journal of Engineering Mechanics, 2021, 147(10): 04021061 [Google Scholar]

[10] FRANCO N, MANZONI A, ZUNINO P. A deep learning approach to reduced order modelling of parameter dependent partial differential equations[J]. Mathematics of Computation, 2022, 92(340): 483–524 [Google Scholar]

[11] WU P, GONG S, PAN K, et al. Reduced order model using convolutional auto-encoder with self-attention[J]. Physics of Fluids, 2021, 33(7): 077107 [Google Scholar]