| Issue |
JNWPU
Volume 43, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 326 - 337 | |
| DOI | https://doi.org/10.1051/jnwpu/20254320326 | |
| Published online | 04 June 2025 | |
Design of large signal stabilization strategy for DC-DC converter in multi-electric aircraft DC power supply system
多电飞机直流供电系统DC-DC变换器大信号致稳策略设计
1
School of Electric Engineering, Sichuan University, Chengdu 610041, China
2
School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
3
Northwest University of Political Science and Law, Xi'an 710100, China
Received:
11
March
2024
A large number of constant power loads with negative impedance characteristics are connected to the power supply system of the multi-electric aircraft, which poses great threats to the system stability. In order to ensure the stability and reliability of the multi-electric aircraft power supply system, the negative impedance feature of constant power loads must be overcome. In this paper, a novel backstepping control strategy based on nonlinear disturbance observer is designed for source-side Buck-Boost converter in the DC power supply system of multi-electric aircraft. The average state space model is converted to Brunovsky standard form by feedback linearization method, furthermore, the disturbances and uncertainties of the system are estimated by using the observer technique. Then the estimations are used as feedforward signals to design a novel backstepping controller, which guarantees the stability of the regulated power supply system. Finally, the effectiveness of the control strategy is verified by simulations and experiments.
摘要
具有负阻抗特性的恒功率负载大量接入多电飞机直流供电系统, 对其稳定运行产生了巨大威胁。为保证多电飞机直流供电系统的稳定性与可靠性, 必须克服恒功率负载负阻抗特性带来的负面影响。针对多电飞机直流供电系统中源侧Buck-Boost接口变换器系统, 设计了一种新的基于非线性扰动观测器的反步控制策略。通过反馈线性化方法将平均状态空间模型转换为布鲁诺夫斯基标准形式; 利用观测器对系统存在的干扰和不确定性进行估计, 并将观测器估计作为前馈信号设计反步控制律, 保证了系统母线电压的大信号稳定; 通过仿真和实验等手段验证了该控制策略的有效性。
Key words: multi-electric aircraft / DC power system / backstepping control / constant power load / Buck-Boost converter / large signal stability
关键字 : 多电飞机 / 直流供电系统 / 反步控制 / 恒功率负载 / Buck-Boost变换器 / 大信号稳定
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着“碳达峰、碳中和”的“双碳”目标的提出,如何在航空运输业减少温室气体排放成为了关注焦点之一[1–2]。多电飞机相较于传统飞机, 使用电能作为二次能源, 能够有效减少温室气体和污染物排放,解决系统可靠性不足、燃油经济成本过高等问题, 是发展绿色航空的重要途径[3–4]。
飞机供电系统作为多电飞机的重要组成部分, 发展初期一般使用低压直流供电系统。随着多电飞机技术的发展, 飞机的用电量和用电形式不断增加, 作为低压供电系统的延伸, 高压直流供电系统具有质量轻、功率密度大、抗扰能力强、相比于交流系统更容易实现并联供电等诸多优点[5–6]。高压直流供电系统已成为未来多电飞机供电系统的重要发展方向[7]。高压直流供电系统具有巨大的优势, 但在系统稳定性问题上也面临巨大的挑战。在多电飞机供电系统中, 大量采用现代电力电子变换器和伺服电机驱动系统进行电能变换[8], 然而随着越来越多表现为恒功率负载(constant power load, CPL)特性的电力电子设备接入, 系统的有效阻尼大幅度降低, 给系统的稳定性和可靠性均带来了巨大的挑战。尤其是在复杂工况下, 恒功率负载功率的大范围波动甚至会导致供电系统直流母线电压的彻底崩溃, 造成机毁人亡的严重后果[9–10]。因此, 针对多电飞机供电系统设计一种先进的控制策略, 以此消除CPL带来的不良影响, 从而保证系统的稳定性是非常必要的[11–12]。
为解决上述问题, 诸多学者进行了大量的研究。如文献[13–14]通过增加受控系统阻尼的方法增强系统的稳定性。这一类无源控制方法虽然设计简单、易于实现[15], 但无源阻尼装置增加了系统的体积和功率损耗。为克服这一缺点, 近年来许多国内外学者提出了大量有源阻尼控制策略。文献[16]针对源侧直流变流器, 构建了虚拟电阻从而有效减小了变流器与LC滤波电路并联阻抗的谐振峰值。文献[17]设计了一种基于并网变换器直流电流前馈的有源阻尼方法。文献[18]提出了一种虚拟电阻控制策略, 有效增强了系统阻尼。虽然上述有源阻尼设计方法均在一定程度上提高了系统稳定裕度, 但其基于小信号模型设计的特点只能保证受控系统在特定平衡点极小临域的稳定性[19]。但在多电飞机实际应用中, 因飞机频繁切换飞行姿态、应对复杂外界干扰等引起的大范围功率波动易使系统脱离其小信号稳定域, 导致系统失稳。因此如何确保多电飞机供电系统在复杂工况下的大信号稳定性仍是亟待解决的问题。针对系统存在大扰动的情况, 文献[20]提出了一种复合离散滑膜控制方法, 该方法保证了系统具有良好的鲁棒性, 但存在不可避免的抖颤问题。文献[21–22]采用了模型预测控制(MPC)算法来满足大信号稳定性的控制要求, 但因对控制器运算能力的极高要求而限制了其实际应用。文献[23]提出的控制方法能够保证系统的大信号稳定, 但其对于输入电压传感器的依赖增加了控制器的实现成本。
因此, 考虑到上述控制方法的不足, 针对带CPL负载供电系统的大信号稳定问题, 本文提出一种新的基于非线性扰动观测器(nonlinear disturbance observer, NDO)的反步控制策略, 克服了小信号控制策略难以消弭大信号非线性扰动的缺点。NDO是对系统不确定项和扰动量进行估计和补偿的有效方法, 具有较快的收敛速度[24], 能有效改善变换器系统的动态性能, 节约系统硬件成本[25]。反步控制在系统存在不确定项和外界扰动等影响时, 作为一种有效解决系统稳定性和参考值跟踪问题的系统性控制方法[26], 可以使得多电飞机供电系统具有较高的跟踪精度和较强的抗扰能力, 为其稳定运行提供保障[27]。本文的主要工作和创新点如下:
1) 对带有恒功率负载的Buck-Boost变换器系统建立平均状态空间模型, 对模型正确性进行了验证。之后基于微分同胚原理将该模型转换为布鲁诺夫斯基标准形式, 在不损失系统非线性特性的前提下实现了系统模型的线性化。此标准形式具有通用性, 可适用于不同的变换器模型, 有利于对变换器建立统一的模块化模型。
2) 基于平均状态空间模型设计了NDO, 以NDO的估计输出值作为控制器的前馈量, 实现了输入电压起伏、负载功率波动等大信号扰动时, 观测器对扰动量的及时估计, 使得系统在已知参数少、模型存在不确定项和外部扰动的情况下也能快速准确地跟踪输出电压参考值, 为系统提供更快的动态响应速度, 节约系统硬件成本。
3) 设计了一种新的反步控制策略, 与传统小信号控制策略相比, 考虑了更大范围的扰动类别, 消弭了大信号非线性扰动对系统造成的严重不利影响, 实现在复杂工况下的母线电压支撑。此外, 与上述方法相比, 本文所提反步控制策略在数学推导上形式简单、泛用性较高, 经过简单修改, 便可直接应用于不同类型的变换器, 为研究多电飞机高压直流供电系统统一化的控制方法提供了参考。
本文所使用的符号注释在表 1中列出。
图 1为多电飞机高压直流供电系统结构图[6], 直流电源主要由燃料电池、锂电池等构成, 不同电压等级的电源产生的电压通过DC/DC变换器转换后, 为直流母线供电, 负载侧则由阻性负载和CPL负载等多种负载构成。其中Buck-Boost变换器因同时具有升/降压2种功能而得到广泛运用, 因此本文选取Buck-Boost变换器为控制对象。
图 2为Buck-Boost变换器简化结构图, 其中E为Buck-Boost变换器的输入电压, S为开关管, u为占空比, D为二极管, C, L分别为电容和电感, R为阻性负载, 恒功率负载以理想电流源代替, 其功率为PCPL[17, 28]。系统工作在连续导通模式(continuous conduction mode, CCM), 以电感电流iL和电容电压VC为状态变量, 采用状态空间平均法建立其大信号平均模型为[29]
2 模型正确性验证
变换器的平均状态空间模型准确性会直接影响后续控制器设计与分析, 因此在本节中, 首先验证模型的准确性。
2.1 时域验证
为在时域上验证所提出模型的准确性, 使用MATLAB/Simulink进行了仿真实验。图 3为在占空比变化的情况下变换器输出电压的瞬态响应波形, 其中蓝色实线为数学模型输出电压响应波形, 红色虚线为电路仿真输出电压响应波形。设置初始占空比u=0.5, 在t=0.25 s时u上升5%并保持, 在t=0.35 s时恢复到其初始值。从图 3中可以看出, 所提出的数学模型与仿真电路具有较好的一致性。
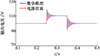 |
图3 时域验证: 输出电压响应 |
2.2 频域验证
为使用频域法验证模型准确性, 推导出(1)式中占空比与输出电压的传递函数为
式中:ṽo和ũ分别表示占空比和输出电压的小信号干扰量;Vref为直流母线电压vo的参考值。传递函数的频域响应与MATLAB/Simulink中搭建的Buck-Boost变换器电路的频域响应如图 4所示, 其中蓝色实线为数学模型的频域响应, 而红色星形则是仿真电路的响应曲线, 两者高度重合, 验证了所搭建模型的频域有效性。
基于上述分析与实验结果, 所提出平均状态空间模型的准确性得到了验证,适用于基于小信号法和大信号法的Buck-Boost变换器控制策略设计。
 |
图4 输出电压与占空比的频率响应关系 |
3 反步控制器设计
在本节中, 设计了基于NDO的反步控制策略, 确保了Buck-Boost变换器系统在大信号扰动下的稳定性和鲁棒性, 并使直流母线电压vo跟踪其参考值Vref。反步控制框图如图 5所示。
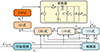 |
图5 反步控制框图 |
3.1 坐标变换
Buck-Boost变换器具有典型的非线性特征。因此, 为便于控制器设计, 首先利用反馈线性化技术进行坐标转换, 将总存储能量和输入功率定义为新的状态变量, 将模型转换为布鲁诺夫斯基标准形式如(3)式所示。
式中:x1为总存储能量;x2为输入功率。其表达式分别为
d1为系统扰动, 可表示为
d2为不确定项引起的系统扰动, 如参数误差、寄生电路参数等。k为间接控制率,联立(1)式和(4)式, 可得系统实际控制率uk为
经过坐标变换后, 控制目标从完成直流母线电压的跟踪变更为实现x1, x2分别渐进收敛于其参考值x1ref, x2ref。x1ref和x2ref的表达式为
式中,Iref为电感电流iL的参考值。Iref可表示为
式中,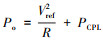 , 为系统稳态时的输出总功率。
, 为系统稳态时的输出总功率。
干扰项d1和d2由系统的电压、功率、电容电感寄生参数等实际物理量构成, 考虑到实际情况, 通常d1和d2本身及其导数是有界的。此外, 相较于所设计控制器的响应速度, 系统干扰量的变化频率较低, 因此在一个控制周期内, 干扰量可被视为常数。根据上述分析, 可以做出以下假设[11]:
假设1 干扰项di及其导数 有界, 并满足
有界, 并满足
假设2  满足
满足  , i∈{1, 2}
, i∈{1, 2}
3.2 非线性扰动观测器设计
在系统实际运行过程中, 输出功率容易受到各种干扰影响, 并且系统模型参数的不确定性等同样也会对控制效果产生影响, 这些因素对控制效果的影响主要体现在干扰项d1和d2上。本节将设计观测器获取d1和d2的估计值以消除未知干扰对于受控系统的影响。
引理1 若系统ẋ=f(x(t), d(t))满足全局输入状态稳定性(input-to-state stable, ISS), 且输入满足  , 则系统状态变量满足
, 则系统状态变量满足  。
。
为便于观测器设计, 将(3)式转换为状态空间方程形式
式中, , 单位矩阵
, 单位矩阵  。
。
式中: 为系统扰动d的估计值;ψ为扰动观测器的中间变量;p(x)为待设计的函数;l(x)为自定义的扰动观测器增益, 且
为系统扰动d的估计值;ψ为扰动观测器的中间变量;p(x)为待设计的函数;l(x)为自定义的扰动观测器增益, 且 。l(x)可记为
。l(x)可记为
根据(10)式, 定义扰动估计误差为
观测器有效性证明如下。
对(12)式进行求导可得
由假设2和引理1:在系统  中, 有
中, 有 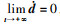 , 则
, 则 , 即观测误差最终可收敛于0, 观测值可以实现对实际值的跟踪。
, 即观测误差最终可收敛于0, 观测值可以实现对实际值的跟踪。
3.3 控制器设计
由于在实际应用中, 难以测量总输出功率Po的准确值, 因此根据(5)式和(10)式, 可得Po的估计值  为
为
将(8)式和(14)式代入(7)式, 得到状态变量的估计值表达式为
式中, ,
,  分别是x1ref, x2ref的估计值。
分别是x1ref, x2ref的估计值。
定义状态变量误差为
且定义中间变量Z1和Z2为
式中,α1为虚拟控制率。
由(17)式可得Z1, Z2对时间的导数为
α1和k分别设计为
式中:δ(t)=ae-bt, a, b, K1, K2为任意正实数。
3.4 稳定性分析
选取李雅普诺夫函数为
对V1进行求导, 并将(18)~(19)式代入其导数, 可得
由不等式
则(22)式可化简为
由(24)式可知, 若选取V1为李雅普诺夫函数, 其导数不能满足李雅普诺夫负定条件, 因此选取新的李雅普诺夫函数V2为
其对时间的导数为
式中,K*的定义为
求解(26)式可得
由(28)式可得
因为有V2(t)≥0恒成立, 联立(25)式、(29)式, 可得
将(30)式代入(17)式, 则有
由α1定义可知
联立(31)式和(32)式, 可得
即当有t→+∞时, 有x1→  , x2→
, x2→ 。
。
根据(13)式、(31)式、(33)式, 可以证明本文所设计基于NDO的反步控制器能够保证系统渐进稳定。本文为解决NDO和控制器收敛时间的配合问题, 通过调整NDO和控制器的控制参量l(x)以及K*来决定各部分收敛速度的快慢(即带宽的大小), 保证NDO的带宽大于控制器的带宽, 以此保证观测估计量前馈的及时性和有效性, 从而提高受控系统的响应速度和稳定域。
4 参数设计与仿真实验
为验证所提控制器设计的有效性, 在MATLAB/Simulink环境中进行3组仿真实验。第一组仿真实验给出了观测器增益选择的基本准则, 为更接近工程实际应用场景, 其余2组仿真实验分别基于混合负载和纯恒功率负载条件, 在多种工况下, 验证了系统在所提控制策略下的稳定性和鲁棒性。电路参数如表 2所示。
仿真电路参数
4.1 控制器参数设计
图 6~7分别对比了观测器增益L1不同选值对系统输出电压暂态特性和d1观测效果的影响。在纯恒功率负载运行条件下, 恒功率负载初始功率为1 kW, 在t=0.1 s时, 由1 kW突变至2 kW。图 6给出了在L2=1 000时, 不同L1取值下系统输出电压的瞬态响应, 随着L1值的增大, 变换器输出电压整定时间减小。由图 7可知, 其取值越大, 观测器对d1的观测收敛速度越快, 观测效果越好, 但L1值过大会导致超调量较大。综合考虑上述影响, 最终选取L1=1 600, 此时输出电压超调量不到1%, 收敛时间约为5 ms。
图 8和图 9分别展示了在L1=1 600的前提下, 观测器不同L2的取值对系统输出电压和d1观测效果的影响。
由图 8可知, L2取值为1 000时, 变换器输出电压整定时间和超调量都最小。此外, 与L1类似, L2值过大或过小, 都会导致超调量增大。如图 9所示, 不同L2取值对d1观测效果几乎无影响。因此, 主要考虑L2对变换器输出电压暂态响应的影响, 最终选取L2=1 000。
 |
图6 观测器参数变化下的输出电压动态响应 |
 |
图7 观测器参数变化下的d1值 |
 |
图8 观测器参数变化下的输出电压动态响应 |
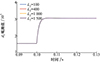 |
图9 观测器参数变化下的d1值 |
4.2 混合功率负载测试
在本节中, 综合考虑阻性负载R和恒功率负载共同作用的工况下, 对所提反步控制策略的有效性进行验证。在高压直流供电系统中, 270 V供电系统是多电飞机供电系统的主要架构之一[7]。因此, 为证明本文所设计控制器的有效性, 以多电飞机270 V供电系统为例, 选取目前较为广泛采用的MIL-STD-704F标准[32–33], 分别进行参考电压跟踪、恒功率负载扰动以及输入电压扰动实验。
4.2.1 参考电压跟踪实验
各类标准对多电飞机高压直流供电系统的性能都有严格规定, 其中MIL-STD-704F标准要求供电系统稳态时电压值最高为280 V、最低为250 V[34]。因此, 在图 10的仿真结果中, 选取参考电压初始值为270 V, 之后在t=0.15, 0.2, 0.25 s时, 电压参考值分别设置为250, 270, 280 V。由图 10可知, 输出电压都能在10 ms的时间内完成对参考电压值的跟踪, 且超调量小, 满足MIL-STD-704F标准。
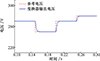 |
图10 参考电压跟踪波形图(混合功率负载) |
4.2.2 恒功率负载扰动实验
MIL-STD-704F标准规定多电飞机供电系统暂态过程中电压最高值不超过330 V, 且时间不超过20 ms, 电压最低值不低于200 V, 且时间不超过10 ms[34]。在混合负载工况以及纯恒功率负载工况下, CPL功率值发生突变时系统变换器的输出电压暂态响应情况在图 11中给出。CPL的初始功率值设置为1 kW, 分别在t=0.15, 0.2, 0.25 s时, 跃变至2, 3, 4 kW。由图 11可知, 系统变换器输出电压在暂态过程中, 电压波动最高值远远小于330 V, 最低值远远大于200 V, 满足暂态时间标准。
 |
图11 恒功率负载扰动下的输出电压及功率 |
4.2.3 输入电压扰动实验
参考文献[33]的工况, 初始输入电压值设定为125 V, t=0.15 s时模拟供电系统对外供电的情况, 输入电压降至91 V; t=0.2 s时, 输入电压继续下降至65 V; 此后t=0.25 s时, 系统进行充电, 输入电压回升至91 V。图 12展示了在混合负载工况下的变换器输出电压波动情况。从图 12可得, 变换器输出电压暂态过程满足MIL-STD-704F标准, 所提控制器满足系统稳定性和鲁棒性要求。
 |
图12 输入电压扰动下的输出电压 |
4.3 纯恒功率负载测试
为模拟系统工作环境最恶劣的情况, 去除了恒阻抗负载, 本节的所有仿真都在纯恒功率负载工况下完成。
4.3.1 参考电压跟踪实验
与混合功率负载工况下测试类似, 由图 13可知, 在纯恒功率负载工况下, 参考电压变化时, 系统依然满足MIL-STD-704F标准。
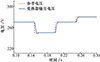 |
图13 参考电压跟踪波形图(恒功率负载) |
4.3.2 恒功率负载扰动实验
去除恒阻抗负载后, 系统输出总功率即为CPL的输出功率, CPL的扰动变化趋势与混合负载条件下的测试设置相同。从图 14可得, 输出电压波形与混合负载条件下的波形相比较, 虽然系统输出电压的波动略微增加, 但系统整体仍保持稳定, 并且在CPL输出功率突变时, 依然能够在小于10 ms的时间内快速完成调整。
 |
图14 恒功率负载扰动下的输出电压及功率 |
4.3.3 输入电压扰动实验
进一步验证输入电压发生变化时的系统鲁棒性。与4.2节的设定相同, 图 15为输入电压变化下的变换器输出电压波形, 系统仍具有强鲁棒性并保持稳定, 且在基准输出电压为270 V的工况下, 所设计控制器使得系统仍然满MIL-STD-704F标准。
 |
图15 输入电压扰动下的输出电压 |
5 实验验证
为进一步验证本文所设计控制策略有效性, 基于RT-Lab搭建了硬件在环(hardware-in-loop, HIL)实验平台, 如图 16所示, 其中硬件DSP控制器采用TI F28335芯片。同时, 为进一步展示本控制器设计的泛用性, 进行了以参考电压为150 V, 变换器输入电压为100 V的实验验证。
 |
图16 硬件在环实验平台 |
5.1 混合功率负载测试
在本节中, 考虑恒阻抗负载和恒功率负载共同组成混合功率工况下, 对所提反步控制器的有效性及鲁棒性进行验证。
5.1.1 参考电压跟踪实验
图 17展示了输出参考电压阶跃变化时系统动态响应。图 17a)~17b)分别展示了输出参考电压从150 V下降至100 V以及输出参考电压从80 V跃变至100 V系统的动态响应。参考电压在正向和反向阶跃变化后, 输出电压都可以在25 ms内迅速跟踪新的参考电压值。
 |
图17 参考电压跟踪实验波形 |
5.1.2 恒功率负载扰动实验
图 18展示了CPL的功率值发生变化时系统的动态响应。初始CPL功率设置为1 kW, 之后依次上升至2 kW和3 kW。由图 18可知, 系统输出电压始终紧密跟踪其参考输出电压, 在CPL功率产生波动时, 系统输出电压以较小的电压跌落和较短的暂态响应时间(小于10 ms)重新恢复到其参考值。
 |
图18 恒功率负载扰动下的实验波形 |
5.1.3 输入电压扰动实验
图 19为输入电压发生变化时的系统动态响应, 实验期间保持恒功率负载功率为1kW和输出参考电压为150 V。图 19a)~19b)分别展示了输入电压从100 V下降至80 V以及从100 V跃迁至150 V系统的动态响应。由图 19可得, 输出电压在10 ms内重新调节至其参考值, 实现了快速且稳定的电压跟踪。
 |
图19 输入电压扰动下的实验波形 |
5.2 纯恒功率负载测试
为验证系统在稳定性恶劣条件下的有效性, 去除阻性负载, 在纯恒功率负载条件下完成实验。
5.2.1 参考电压跟踪实验
与混合功率负载工况下测试相同, 从图 20a)~20b)可以看出, 变换器的输出电压仍旧能够在短时间内(小于25 ms)完成调节, 保持对参考值的跟踪, 保证系统的稳定性。
 |
图20 恒功率负载下参考电压跟踪实验波形 |
5.2.2 恒功率负载扰动实验
图 21为恒功率负载扰动下的系统动态响应, 恒功率负载从1 kW跃迁至2 kW, 然后继续上升至3 kW。从图 21可以看出, 系统输出电压虽然略有波动, 但依然能够在10 ms内消除恒功率负载扰动产生的影响, 系统整体仍保持稳定。
 |
图21 恒功率负载下实验波形 |
5.2.3 输入电压扰动实验
图 22展示了输入电压变化时的系统动态响应, 在纯恒功率负载条件下, 仍旧保持恒功率负载功率为1 kW和输出参考电压为150 V的恒定值。图 22展示了输入电压从100 V下降至80 V以及从100 V上升至150 V系统的动态响应。可以看出, 输出电压动态响应以较短的暂态时间(小于20 ms)调节至其参考电压值, 系统具有良好的鲁棒性。
综合上述实验结果, 可得本文所提出的基于NDO的反步控制器能够保证在多种扰动情况下的系统大信号稳定, 具有快速的动态响应和零稳态误差, 实现了精确的输出电压跟踪效果。
 |
图22 恒功率负载下输入电压扰动时的实验波形 |
6 结论
本文旨在解决高比例接入CPL的多电飞机直流供电系统中DC-DC变换器输出电压大信号稳定性问题, 针对Buck-Boost变换器提出了一种新的基于NDO的反步控制方法, 实现了多电飞机供电系统的大信号稳定, 提高了系统的可靠性。该方法首先对系统完成大信号平均模型建立, 并验证此模型的准确性, 然后将系统模型转换为布鲁诺夫斯基标准形式。之后通过NDO对外部扰动以及不确定项进行估计并前馈至控制器, 有效减少了系统对传感器的依赖, 在减少系统成本的前提下, 实现了对变换器输出电压的快速、精确跟踪, 保证了系统的稳定性和鲁棒性。为验证所提控制器的有效性和泛用性, 分别搭建MATLAB/Simulink仿真实验平台以及HIL实验平台。仿真和实验结果表明, 该控制器在抵抗输入输出电压扰动、CPL功率扰动上均具有明显优势, 能够有效保证系统的大信号稳定, 系统具有良好的跟踪精度和快速的动态响应, 且该控制器设计简单、具有广泛的适用性, 具有推广到其他工业应用场景的价值。
References
- LI Xiangke, DONG Chaoyu, ZHAO Xin, et al. Large-signal stability control strategy of portable vehicle-mounted high-gain DC-DC converter: backstepping technique based on disturbance observer[J]. Proceedings of the CSEE, 2023, 43(7): 2790–2802 (in Chinese) [Google Scholar]
- ZHANG Zhuoran, XU Yanwu, YAO Yiming, et al. Power system and key technologies of more electric aircraft[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2022, 54(5): 969–984 (in Chinese) [Google Scholar]
- LIU Yongzhi, NIE Kai, YU Jinlu, et al. Small-signal stability analysis of 270 V high-voltage DC power system for more electric aircraft[J]. Journal of Air Force Engineering University, 2021, 22(4): 35–40. [Article] (in Chinese) [Google Scholar]
- SONG Qingchao, CHEN Jiawei, CAI Kuncheng, et al. High-reliability dynamic power allocation technology for hybrid power supply system of fuel cell-battery-supercapacitor in more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445–458 (in Chinese) [Google Scholar]
- WEI Li, WANG Huizhen, YAN Yangguang, et al. Development trend and research status of aircraft starter/generator system[J]. Aeronautical Science and Technology, 2010(5): 28–32. [Article] (in Chinese) [Google Scholar]
- SUN Yu. Research on electrical load characteristics of more electric aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017 (in Chinese) [Google Scholar]
- LI Yongdong, ZHANG Xuan, XU Lie. Review of stability research on high-voltage DC power supply system for more electric aircraft[J]. Journal of Power Supply, 2017, 15(2): 2–11 (in Chinese) [Google Scholar]
- MOU Chengming. Stability analysis of power system in more electric aircraft[D]. Chengdu: University of Electronic Science and Technology of China, 2019 (in Chinese) [Google Scholar]
- LI X K, ZHANG X N, JIANG W T, et al. A novel assorted nonlinear stabilizer for DC-DC multilevel boost converter with constant power load in DC microgrid[J]. IEEE Trans on Power Electronics, 2020, 35(10): 11181–11192. [Article] [Google Scholar]
- ZENG Guohui, LIAO Hongfei, ZHAO Jinbin, et al. Adaptive control strategy for virtual inertia and damping coefficient of bidirectional DC/DC converter in DC microgrid[J]. Power System Protection and Control, 2022, 50(6): 65–73 (in Chinese) [Google Scholar]
- JIANG W, ZHANG X, GUO F, et al. Large-signal stability of interleave boost converter system with constant power load using sliding-mode control[J]. IEEE Trans on Industrial Electronics, 2019, 67(11): 9450–9459 [Google Scholar]
- WU Han, JIA Yanbing, HAN Xiaoqing, et al. Control strategy for dual-active-bridge converter based on kalman filter and deep reinforcement learning[J]. High Voltage Engineering, 2024, 50(2): 714–724 (in Chinese) [Google Scholar]
- MIDDLEBROOK R D. Input filter consideration in design and application of switching regulators[C]//IEEE Industry Applications Society Annual Meeting, 1976: 366–382 [Google Scholar]
- ALI M, KNEBUSCH B, JUENEMANN L, et al. Design and comparison of input filter configurations for SiC-MOSFET-Based automotive DC-AC inverters[C]//2023 25th European Conference on Power Electronics and Applications, 2023: 1–10 [Google Scholar]
- WU Leitao, YANG Zhaohua, XU Bugong. The passive control method of DC/DC switching converter[J]. Transactions of China Electrotechnical Society, 2004(4): 66–69. [Article] (in Chinese) [Google Scholar]
- WU Mingfei, LU D D C. A novel stabilization method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Trans on Industrial Electronics, 2015, 62(7): 4552–4562. [Article] [Google Scholar]
- JI Yu, WANG Dongxu, WU Hongbin, et al. Active damping method to enhance the stability of DC microgrids[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370–379 (in Chinese) [Google Scholar]
- ZHU Xiaorong, MENG Xinxin Stability analysis and research on active damping control of DC microgrids[J]. High Voltage Engineering, 2020, 46(5): 1670–1681 (in Chinese) [Google Scholar]
- TENG Changpeng, WANG Yubin, ZHOU Bokai, et al. Large-signal stability analysis of dc microgrids with constant power loads[J].Transactions of China Electrotechnical Society, 2019, 34(5): 973–982 (in Chinese) [Google Scholar]
- ZHENG C, DRAGIĈEVIĈ T, ZHANG J, et al. Composite robust quasi-sliding mode control of DC-DC buck converter with constant power loads[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1455–1464. [Article] [Google Scholar]
- VAFAMAND N, YOUSEFIZADEH S, KHOOBAN M H, et al. Adaptive TS fuzzy-based MPC for DC microgrids with dynamic CPLS: nonlinear power observer approach[J]. IEEE Systems Journal, 2019, 13(3): 3203–3210. [Article] [Google Scholar]
- XU Q, YAN Y, ZHANG C, et al. An offset-free composite model predictive control strategy for DC/DC buck converter feeding constant power loads[J]. IEEE Trans Power Electron, 2020, 35(5): 5331–5342. [Article] [Google Scholar]
- YUAN Cong, BAI Hao, MA Rui, et al. Large-signal stability analysis and design of finite-time controller for the electric vehicle DC power system[J]. IEEE Trans on Industry Applications, 2022, 58(1): 868–878. [Article] [Google Scholar]
- ZHANG C, YAN Y, WEN C, et al. A nonsmooth composite control design framework for nonlinear systems with mismatched disturbances: algorithms and experimental tests[J]. IEEE Trans on Industrial Electronics, 2018, 65(11): 8828–8839. [Article] [Google Scholar]
- SU Yong, CHEN Yanfeng. Nonsingular terminal sliding mode control strategy for energy storage bidirectional DC-DC converter based on nonlinear disturbance observer[J]. Energy Storage Science and Technology, 2024, 13(5): 1523–1531 (in Chinese) [Google Scholar]
- ZHAO X D, WANG X Y, ZHANG S, et al. Adaptive neural backstepping control design for a class of nonsmooth nonlinear systems[J]. IEEE Trans on Systems Man Cybernetics-Systems, 2019, 49(9): 1820–1831. [Article] [Google Scholar]
- LIU Xiaodong, JIA Chenhui, ZHANG Yu, et al. Reinforcement learning-based backstepping control method for cruise aircraft[C]//Proceedings of the 42nd Chinese Conference, 2023 (in Chinese) [Google Scholar]
- ZHANG Zehua, SONG Guiying, ZHANG Xiaolu, et al. Stability and robustness control strategy for DC microgrids considering constant power loads[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391–4405 (in Chinese) [Google Scholar]
- LU X, SUN K, GUERRERO J M, et al. Stability enhancement based on virtual impedance for DC microgrids with constant power loads[J]. IEEE Trans on Smart Grid, 2015, 6(6): 2770–2783. [Article] [Google Scholar]
- CHEN W H. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 161–166. [Article] [Google Scholar]
- LI Chuanxu, MENG Xiuyun, WANG Jie. Design of flight vehicle trajectory tracking controller based on disturbance observer[J]. Systems Engineering and Electronics, 2022, 44(8): 2593–2600 (in Chinese) [Google Scholar]
- XU Yanwu. Fundamental research on high-voltage DC parallel power supply system for doubly salient electromechanical converter in more electric aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2023 (in Chinese) [Google Scholar]
- CHEN J, SONG Q, YIN S, et al. On the decentralized energy management strategy for the all-electric APU of future more electric aircraft composed of multiple fuel cells and supercapacitors[J]. IEEE Trans on Industrial Electronics, 2019, 67(8): 6183–6194 [Google Scholar]
- GAO F. Decentralised control and stability analysis of a multi-generator based electrical power system for more electric aircraft[D]. Nottingham: University of Nottingham, 2016 [Google Scholar]
All Tables
All Figures
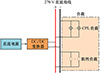 |
图1 多电飞机高压直流供电系统结构图 |
| In the text | |
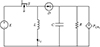 |
图2 多电飞机中Buck-Boost变换器拓扑 |
| In the text | |
 |
图3 时域验证: 输出电压响应 |
| In the text | |
 |
图4 输出电压与占空比的频率响应关系 |
| In the text | |
 |
图5 反步控制框图 |
| In the text | |
 |
图6 观测器参数变化下的输出电压动态响应 |
| In the text | |
 |
图7 观测器参数变化下的d1值 |
| In the text | |
 |
图8 观测器参数变化下的输出电压动态响应 |
| In the text | |
 |
图9 观测器参数变化下的d1值 |
| In the text | |
 |
图10 参考电压跟踪波形图(混合功率负载) |
| In the text | |
 |
图11 恒功率负载扰动下的输出电压及功率 |
| In the text | |
 |
图12 输入电压扰动下的输出电压 |
| In the text | |
 |
图13 参考电压跟踪波形图(恒功率负载) |
| In the text | |
 |
图14 恒功率负载扰动下的输出电压及功率 |
| In the text | |
 |
图15 输入电压扰动下的输出电压 |
| In the text | |
 |
图16 硬件在环实验平台 |
| In the text | |
 |
图17 参考电压跟踪实验波形 |
| In the text | |
 |
图18 恒功率负载扰动下的实验波形 |
| In the text | |
 |
图19 输入电压扰动下的实验波形 |
| In the text | |
 |
图20 恒功率负载下参考电压跟踪实验波形 |
| In the text | |
 |
图21 恒功率负载下实验波形 |
| In the text | |
 |
图22 恒功率负载下输入电压扰动时的实验波形 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


