| Issue |
JNWPU
Volume 42, Number 4, August 2024
|
|
|---|---|---|
| Page(s) | 673 - 682 | |
| DOI | https://doi.org/10.1051/jnwpu/20244240673 | |
| Published online | 08 October 2024 | |
Speed regulation system based on proportional resonance self-coupling PI control
基于比例谐振自耦PI控制的调速系统
1
School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
2
AVIC Lanzhou Wanli Aviation Electromechanical Co., Ltd, Lanzhou 730070, China
3
Key Laboratory of Aircraft-Electromechanical Actuators of Gansu Province, Lanzhou 730070, China
Received:
11
July
2023
In this paper, an improved self-coupled PI control dual-loop control strategy is proposed for the vector control of permanent magnet synchronous electric speed control system, to improve the poor motor control effect caused by the dead zone of the inverter, the presence of harmonics in the motor magnetic field distribution, and the error in the sampling process of the current. In order to reduce the tracking error of the signal, an acceleration feed-forward method is adopted, and the self-coupled PI controller with an additional Levant differentiator is introduced into the speed loop of the permanent magnet synchronous motor to ensure the accurate derivation of the input signal containing noise to improve the robustness of the system. In addition, this strategy combines the proportional term of the autotuned PI control structure with the standard resonator to form a proportional resonant autotuned PI in the current loop, so that the permanent magnet synchronous motor can better compensate the current in the current loop control to achieve the effect of current harmonic suppression. Finally, the control mechanism of the servo system analyzed, and based on the mathematical model of the controlled object PMSM, the design method of the improved self-coupling PI control structure is given. The experimental results show that the proposed control strategy can reduce the impact of the motor's own parameter changes on the system performance and has a good current harmonic suppression in the low-speed domain, which verifies the effectiveness of the designed improved self-coupled PI controller.
摘要
针对永磁同步电机调速系统矢量控制过程中, 逆变器死区、电机磁场分布谐波以及电流在采样过程中存在误差等因素导致的电机控制效果不佳问题, 提出了一种改进型自耦PI控制的双环控制策略。为减小信号的跟踪误差, 采用加速度前馈的方式, 将增加Levant微分器的自耦PI控制器引入到永磁同步电机速度环中, 确保对含有噪声的输入信号准确求导以提高系统的鲁棒性。另外, 所提策略在电流环中将增加加速前馈的自耦PI控制结构的比例项和标准谐振器相结合, 构成比例谐振自耦PI控制器, 使永磁同步电机在电流环的控制中能更好地补偿电流, 达到抑制电流谐波的作用。通过分析伺服系统的控制机理, 在被控对象PMSM数学模型的基础上, 给出了改进型自耦PI控制结构的设计方法。实验结果表明, 所提出的控制策略能够减小电机自身参数变化对系统性能的影响并且在低速域具有良好的抑制电流谐波作用, 验证了所设计的改进型自耦PI控制器的有效性。
Key words: permanent magnet synchronous motor / proportional resonance self-coupling PI control / nonlinear control / harmonic suppression
关键字 : 永磁同步电机 / 比例谐振自耦PI控制 / 非线性控制 / 谐波抑制
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
永磁同步电机(permanent magnet synchronous motor, PMSM)很受航空机电作动领域工程师的青睐, 因为它具有效率高、启动力矩大、电机机身发热小、允许的过载电流大、运行过程中产生的噪音小、自身结构简单等优点。随着永磁材料性能的提高、高功率电子元器件的发展与应用以及控制理论的发展, 永磁同步电机的控制性能有了很大提高。但同时也存在很多不利于电机控制性能的因素, 如气隙磁场的畸变、逆变器的非线性、电机结构加工误差等, 这些不利因素引入了电流谐波，进而导致了电流畸变的发生[1]。
抑制电流谐波的方法有2种主体思路[2–3]: 一种是提高电机反电势正弦度的方式, 主要通过改善气隙磁场在电机内的分布方式来实现；另一种是对电流谐波进行补偿, 它是从电机控制算法的角度来实现, 主要改善三相逆变器上下桥臂功率管的压降和死区时间等非线性因素。文献[4]采用坐标变化与低通滤波器的方法检测电机电流中5次和7次谐波的含量, 再结合同步旋转坐标变换理论, 将谐波电流环引入原有双闭环系统, 进而提高电机相电流的正弦度, 成功实现了抑制电流谐波的目的。文献[5]通过在传统扩张观测器的扰动估计回路中增加并联准谐振环节, 采用新型准谐振自抗扰控制方法, 增强了系统对电流谐波交流干扰的抑制效果。文献[6]提出在电流控制环路内, 通过连接谐振调节器的方法减少电流谐波, 实现了对特定谐波的有效抑制。文献[7]提出将比例谐振型自抗扰控制设计在电流环内, 以达到完全解耦dq轴电流的目的, 从而抑制各种电流谐波, 有效解决了d轴与q轴电流在永磁同步电机矢量控制中的交叉耦合问题, 并解决了多种谐波干扰的问题。文献[2]通过改进离散域控制器参数设计方法, 针对表贴式永磁同步电机矢量控制系统中固定比例积分谐振控制器参数在不同运行工况下会降低电流谐波抑制效果的问题, 成功改进了表贴式永磁同步电机矢量控制系统中固定比例积分谐振控制器参数的设计方法, 从而在不同转速工况下既能实现系统稳定性又能抑制相电流5次和7次谐波。
本文针对逆变器非线性、电机结构加工误差等因素引起的永磁同步电机调速系统的电流谐波问题, 建立了基于改进型自耦PI(self coupling PI levant resonance, SCPILR)控制的双环控制策略。将带有Levant微分器的自耦PI(self-coupling PI, SC-PI)控制算法引入永磁同步电机速度环控制中, 确保对含有噪声的输入信号准确求导, 提高系统的鲁棒性。电流环在增加Levant微分器的基础上将自耦PI控制结构中比例项和标准谐振器相结合，构成比例谐振自耦PI控制, 达到抑制电流谐波的目的。本文主要分析了伺服系统的扰动机理, 建立了基于自耦PI控制结构和被控对象PMSM的数学模型, 并引入Levant微分器和比例谐振控制器构建了改进型自耦PI控制器, 并对伺服系统的动态响应、抗扰动性能及电流谐波抑制情况进行了研究。
1 永磁同步电机模型和速度控制器设计
1.1 永磁同步电机模型
在两相旋转坐标系下, 常见的矢量控制算法有弱磁控制法、最大转矩法以及d轴电流为0的矢量控制法。本文矢量控制架构采用d轴电流为0的矢量控制。在id=0的情况下, 转矩方程为
式中：Te为转矩; pn为极对数; ψf为永磁体磁链; iq为q轴电流。
在两相旋转坐标系下的运动方程为
式中：TL是负载转矩; J是转动惯量; ω是角速度; B是黏滞摩擦因数; g(t)是系统中的未知扰动。(2)式可变换为
式中,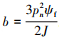 
。
1.2 速度控制器设计
自耦PID控制算法将原本的非线性不确定系统转化为线性不确定系统, 将系统动态和不确定性统一看作总和扰动, 所以其误差动态系统包含总和扰动反馈。
自耦PID控制算法针对不同阶数的非仿射非线性不确定系统, 提出了不同的控制器设计方式, 但总体思路是将原本非线性不确定的控制问题, 转变为文献[8–10]中所述的线性不确定仿射控制问题。因本文涉及的永磁同步电机的速度控制和电流控制, 属于一阶非仿射非线性不确定系统的控制, 故只陈述自耦PI(SC-PI)控制机理。
将永磁同步电机的速度环看成为一阶非仿射非线性不确定系统
式中: d1(t)=-b(iq*-iq)-
为总扰动，包括各种未知干扰的偏差，如q轴电流偏差，摩擦力，外部负载等；ω∈R是可测量状态, iq∈R控制输入, 
是系统函数; iq*为iq的实测值。
总和扰动可描述为一阶非仿射、非线性系统内部未知的不确定因素和外部扰动的统称, 即
式中, b0≠0是控制增益的估计值(不要求精确估计)。将(4)式改写为
显然, (6)式与(4)式是一类一阶线性不确定仿射系统, 二者是等价的。
设被控系统的期望为r, 被控系统输出为w，针对一阶非仿射非线性不确定式系统或其等价的线性不确定仿射系统的控制问题, 定义跟踪控制误差为
定义误差的积分
结合(6)式, 可得
根据(7)~(9)式, 可得受控误差系统
根据文献[10]受控系统定义SC-PI控制器模型为
结合(11)式可将永磁同步电机基于SC-PI控制器的速度环控制器设计为
式中：Iq*是q轴电流指令; ω*为给定转速; b0是SC-PI控制器的参数因子; zc>0是SC-PI控制器的速度因子。以SC-PI控制器为基础的速度环结构框图见图 1。
SC-PI控制器只存在1个速度因子zc, 通过zc将比例和积分2个不同属性的物理环节紧密耦合在一起形成协同控制信号, 其增益整定规则为
在实际工程应用中, 控制器的输入信号经常会带有噪声, 而迅速精确地获取输入信号及其微分是决定控制系统性能的关键问题。为减少系统对输入信号的测量误差和提高对输入噪声的鲁棒性, 采用基于滑模技术的非线性微分器[11]。其基于滑模微分器的二阶表达式为
式中：α>C；λ2≥
, 且C>0。C是输入信号v(t)的导数Lipschitz常数上界。
Levant微分器能够实现x对输入信号v(t)的跟踪, 以及u1对输入微号微分
的跟踪。
因此, 被控对象PMSM的数学模型和Levant微分器的非线性自耦PI控制器设计如图 2所示。Levant微分器的引入使系统的鲁棒性得到了提升, 从而对带有噪声的输入信号的求导更加精确。
 |
图1 基于SC-PI的速度环结构框图 |
 |
图2 基于Levant的速度环SC-PI结构框图 |
2 基于比例谐振SC-PI的电流环控制策略
2.1 在电流环中加入谐振控制器
永磁同步电机电流环的数学模型表达式为
式中，g1(t)和g2(t)是不明干扰。为将id, iq彻底解耦, (15)式变为
式中: dd(t)=g1(t)-Lqωeiq; dq(t)=g2(t)+ωe·(Ldid+ψf), 两者为未知总扰动。
结合(11)式将永磁同步电机的q轴电流控制器设计为
在旋转坐标系下, 由于永磁同步电机驱动系统存在多种电流谐波, 本文采用增加准谐振控制器的方法实现抑制相电流谐波的效果。准谐振控制器的传递函数为
式中：Ki是谐振控制器的增益; ωc是谐振控制器的带宽; ω1是谐振频率。本文以单个标准谐振控制器进行设计, 若有需要可并联多个谐振控制器, 实现对不同频率谐波的抑制。为提高电流谐波的抑制效果, 本文提出了一种基于Levant微分器和比例谐振控制器的SCPILR控制策略, 基于q轴电流的结构框图如图 3所示。
 |
图3 基于SCPILR的q轴电流环结构框图 |
2.2 电流环控制器参数整定
图 4显示了ωc, ω1, zc, Ki取值变化导致比例谐振控制器的变化情况。
从图 4a)可以看出, 设置ωc=2, ω1=20, zc=1, 在仅改变Ki的情况下, 将Ki的值调大会导致谐振控制器在20 rad/s处的增益变大。可以看出Ki的作用是消除稳态误差, 但Ki也不能无限增大, Ki太大会导致谐振控制器的频带范围增大, 也会扩大谐振的影响范围。
从图 4b)可以看出, 设置Ki=10, ω1=20, zc=1, 在仅改变ωc的情况下, 随着ωc的减小，谐振控制器在100 rad/s处的带宽变小。可以看出ωc的作用是信号选择, 谐振控制器的带宽由它决定。
从图 4c)可以看出, 设置Ki=10, ωc=2, zc=1, 在仅改变ω1的情况下, 随着ω1的增大，谐振控制器的谐振频率增大且带宽变小, 起到了不同频率下信号选择的作用。
从图 4d)可以看出, 设置Ki=10, ω2=2, ω1=20, 在仅改变zc的情况下, 随着zc的增大谐振控制器的谐振增益增大且带宽变大程度很明显, 若zc较大会将谐振控制器变成全带宽的控制器, 起不到信号选择的作用。
 |
图4 谐振控制器随各参数变化的伯德图 |
3 实验结果
为验证所提策略的有效性, 采用通过旋变传感器获取转子速度的410 W永磁同步电机, 其主控制芯片采用TI公司的TMS320F28335，速度环和电流环的控制周期为100 μs, 上位机和示波器用于储存和显示实验结果。实验所用给电机参数于表 1中列出, 实验平台如图 5所示。
图 6展示了基于被控对象PMSM的数学模型、Levant微分器和比例谐振控制器的改进型自耦PI的双环控制器设计框图。向Levant微分器输入给定转速, 产生加速度并输出跟踪转速。通过旋变传感器计算后的输出转速和Levant微分器的输出转速的差值、输出转速的微分等作为q轴电流控制器的输入, 用于计算矢量控制所需的转矩电流。电流控制器输入的是转矩电流和励磁电流, 输出的是转矩电压和励磁电压。但是转矩电压和励磁电压无法直接驱动电机运转, 需将此电压变换成三相静止坐标系下的电压, 达到驱动永磁同步电机工作的目的。
其中, PI控制器的参数整定基于Ziegler-Nichols的频域响应方法[12]。通过扫频法获得被控对象的传递函数, 基于Ziegler-Nichols经验公式将电流环中比例参数设置为0.017 5, 积分参数设置为0.000 901, 速度环中比例参数设置为0.035 93, 积分参数设置为0.001 65。基于SC-PI算法的双环控制器的参数整定采用文献[10]提出的方法, b0参数设置为10, 电流环中zc参数设置为0.001, 速度环中zc参数设置为0.25。SCPILR算法中Levant微分器的参数α取值为15, 参数λ取值为10。谐振控制器中, Kr设置为2 000, ωc设置为300, ω0设置为1 000。
PMSM参数
 |
图5 实验平台 |
 |
图6 基于SCPILR双环控制器方框图 |
3.1 速度跟踪及突加负载
在实验测试中, 速度指令为1 000 r/min。图 7展示了PI、SC-PI以及SCPILR 3种控制器在速度指令下发及跟踪过程中，突加0.2 N·m负载时在电机端检测到的速度变化情况。
在调节过程中, PI控制器的峰值速度为1 191 r/min, SC-PI控制器与SCPILR控制器的峰值速度分别为1 010和1 003 r/min, SCPILR控制器超调极小。PI控制器的调节时间为0.526 s, SC-PI控制器的调节时间为0.413 s, SCPILR控制器的调节时间为0.322 s。在进入稳定状态后PI控制器的速度变化小于9 r/min，SC-PI控制器与SCPILR控制器速度变化小于5 r/min。表 2总结了跟踪过程的速度变化。
从表 2可以看出, SC-PI控制器与SCPILR控制器超调的减少是巨大的, SCPILR控制器甚至可以近似为无超调系统。调节时间和稳态误差也有改善。SCPILR控制器相比其他2种控制器在减少超调的同时, 缩短了稳定时间, 实现了阶跃信号的快速平滑跟踪。
从图 7中也可看出, 在突加0.2 N·m负载的时刻, PI控制器速度陡降量为125 r/min, SC-PI控制器速度陡降量为110 r/min, SCPILR控制器速度陡降量为104 r/min。PI控制器调节时间为0.512 s，SC-PI控制器和SCPILR控制器的调节时间为0.510 s。在撤去0.2 N·m负载的时刻, PI控制器速度陡增量为186 r/min, SC-PI控制器速度陡增量为129 r/min, SCPILR控制器速度陡增量为121 r/min。在加载过程中, PI控制器速度稳定值为974 r/min, SC-PI控制器速度稳定值为1 004 r/min, SCPILR控制器速度稳定值为1 001 r/min。说明在负载突变后, SCPILR控制器在速度上的调节能力要比SC-PI控制器和PI控制器更好。表 3总结了突加/突撤负载过程中速度变化情况。
图 8展示了PI、SC-PI以及SCPILR 3种控制算法突加0.2 N·m负载情况下电流Id的变化情况。
从图 8可以看出，PI控制器在加负载之前电流Id的变化量为0.894 1 A，SC-PI控制器的电流Id的变化量为0.840 6 A，SCPILR控制器的电流Id变化量为0.704 5 A。在加上负载之后，PI控制器的电流Id的变化量为0.885 9 A，SC-PI控制器的电流Id的变化量为0.883 A，SCPILR控制器的电流Id变化量为0.782 2 A。可以看出，SCPILR控制器在负载变化前后，在抑制d轴电流波动方面的能力优于SC-PI控制器和PI控制器。
另外，图 8也展现了3种控制器加负载前后的电流Iq的变化情况。其中，PI控制器在加负载之前电流Iq的变化量为0.876 7 A，SC-PI控制器的电流Iq变化量为0.855 1 A，SCPILR控制器的电流Iq变化量为0.712 5 A。在加上负载之后，PI控制器电流Iq变化量为0.795 6 A，SC-PI控制器的电流Iq变化量为0.790 A，SCPILR控制器的电流Iq变化量为0.761 A。表 4列出了加载前后，Id, Iq的变化情况，从表中可以看出，SCPILR控制器在负载变化前后，在抑制q轴电流波动方面的能力优于SC-PI控制器和PI控制器。
 |
图7 速度指令为1 000 r/min及突加负载后, 3种控制器速度跟踪情况 |
速度跟踪过程中各控制器参数对比
突加/突撤负载过程中速度变化情况
 |
图8 3种控制器在突加负载后Id, Iq电流变化情况 |
加载前后, Id, Iq的变化情况
3.2 电机电阻变化
电机在运行过程中, 电机温度会发生变化, 进而导致电机定子电阻变化, 为此通过外接0.1 Ω电阻模拟电机运行过程中电阻的变化情况。图 9展示了PI、SC-PI以及SCPILR 3种控制器在外接0.1 Ω电阻后电流Id, Iq的变化情况。
从图 9可以看出，PI控制器在加负载之前电流Id在变化量为0.878 4 A，SC-PI控制器的电流Id变化量为0.779 2 A，SCPILR控制器的电流Id变化量为0.732 6 A。在加上负载之后，PI控制器的电流Id变化量为0.992 8 A，SC-PI控制器的电流Id变化量为0.835 7 A，SCPILR控制器的电流Id变化量为0.755 7 A。可以看出，SCPILR控制器在外接0.1 Ω电阻前后，在抑制d轴电流波动方面的能力优于SC-PI控制器和PI控制器。
图 9也展现了3种控制器电流Iq的变化情况。其中，PI控制器在加负载之前电流Iq变化量为0.718 2 A，SC-PI控制器的电流Iq变化量为0.680 8 A，SCPILR控制器的电流Iq变化量为0.670 5 A。在加上负载之后，PI控制器的Iq电流的变化量为0.793 3 A，SC-PI控制器的电流Iq变化量为0.770 9 A，SCPILR控制器的电流Iq变化量为0.75 A。具体外接0.1 Ω电阻，Id, Iq加载前后变化情况在表 5中列出。从表 5中可以看出，SCPILR控制器在外接0.1 Ω电阻前后，在抑制d轴和q电流波动方面的能力优于SC-PI控制器和PI控制器。SCPILR控制器受电阻变化的影响不明显。
 |
图9 外加0.1 Ω电阻后3种控制器速度跟踪下电流Id, Iq变化情况 |
外接0.1 Ω电阻, Id, Iq加载前后变化情况
3.3 相电流实验(死区时间2 μs, 转速300 r/min)
本文使用的电机是一款自主设计的电机, 它的转子为永磁体, 在低速运转时需要克服齿槽转矩, 在此期间电机会产生转矩波动, 从而导致电机低速时转速不稳现象的出现，即此电机在低速时性能比高速时略差。因此，故选取300 r/min的转速点, 研究电机在低速时的电流谐波特性。
从图 10中可知, 若采用传统的PI控制器方法控制电流环, 其A相电流中会含有较为明显的5, 7次谐波, 总谐波失真为9.53%, 其含量分别为1.81%, 3.58%。以SC-PI控制器方法计算, 总谐波失真为8.60%, 其总谐波失真较传统电流环PI控制器降低0.93%, A相电流中含有1.43%的5次谐波和2.02%的7次谐波, 5次谐波和7次谐波的含量较传统电流环PI控制器均有所减少。而SCPILR控制器的总谐波失真为7.33%, A相电流中含有1.87%的5次谐波和0.47%的7次谐波。这表明, SCPILR控制器与传统PI控制器相比, 5次谐波虽略有增加, 但整体谐波失真却减少了2.2%, 7次谐波含量减少了3.38%, 高次谐波明显减少。实验结果表明, 在低转速段, 本文提出的方法具有明显的谐振抑制能力。
 |
图10 在300 r/min、死区时间2 us时3种控制器的实验结果谐波分析 |
4 结论
本文提出的SCPILR控制器保证了系统的抗扰性能, 考虑了噪声、负载突变、电阻参数变化及非线性和未建模的不确定性。SCPILR控制器的参数数量少且参数整定非常简单实用, 无需借助复杂的非线性数学工具。实验结果表明, 无需额外的补偿方法即可改善负载突变、电阻参数变化对电机的影响。此外, 还验证了所提控制方法在低速段具有明显的谐波抑制能力。至此，本文提出的改进型自耦PI控制器的有效性得到了验证。
References
- QIAN W, PANDA S K, XU J X. Torque ripple minimization in PM synchronous motors using iterative learning control[J]. IEEE Trans on Power Electronics, 201419(2): 272–279 [Google Scholar]
- WANG Zhijie, JIANG Zhe, LI Zheng, et al. Current harmonic suppression strategy for PMSM based on improved PIR control in discrete domain[J]. Electric Machines and Control, 2023(12): 194–202 (in Chinese) [Google Scholar]
- DAJAKU G, XIE W, GERLING D. Reduction of low space harmonics for the fraction slot concentrated windings using a novel stator design[J]. IEEE Trans on Magnetics, 2014, 50(5): 1–12 [NASA ADS] [CrossRef] [Google Scholar]
- LIU Gang, SUN Qingwen, XIAO Yeran. Permanent magnet synchronous motor current harmonics suppression based on coordinate transformation[J]. Electric Machines and Control, 201519(5): 30–36 (in Chinese) [Google Scholar]
- XU Jiaqun, WANG Tianqi, JIA Pufan. Quasi-resonant active disturbance rejection control for current harmonics suppression of permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2023, 43(6): 2450–2459 [Google Scholar]
- LI Yituo, LU Haifeng, QU Wenlong, et al. A permanent magnet synchronous motor current suppression method based on resonant controllers[J]. Proceedings of the CSEE, 2014, 34(3): 423–430 (in Chinese) [Google Scholar]
- CHEN Zhe, ZHANG Xuxuan, LIU Chunqianget al. Research on current decoupling and harmonic suppression strategy of permanent magnet synchronous motor based on proportional resonance type ADRC[J]. Proceedings of the CSEE, 202242(24): 9062–9071 (in Chinese) [Google Scholar]
- SU Jie, ZENG Zhezhao. Auto-coupling PID control method for nonlinear time varying systems[J]. Control Theory and Technology, 202239(2): 299–306 (in Chinese) [Google Scholar]
- ZENG Zhezhao, CHEN Zeyu. On control theory of PID and auto-coupling PID[J]. Control Theory and Technology, 202037(12): 2654–2662 (in Chinese) [Google Scholar]
- ZENG Zhezhao, LIU Wenjue. Self-coupling PID controllers[J]. Acta Automatica Sinica, 2021, 47(2): 404–422 (in Chinese) [Google Scholar]
- LEVANT A. Robust exact differentiation via sliding mode technique[J]. Automatica, 199834: 379–384 [CrossRef] [MathSciNet] [Google Scholar]
- ZIEGLER J G, NICHOLS N B. Optimum settings for automatics controllers[J]. Transaction of ASME, 1942, 64: 759–768 [Google Scholar]
All Tables
All Figures
|
图1 基于SC-PI的速度环结构框图 |
| In the text | |
|
图2 基于Levant的速度环SC-PI结构框图 |
| In the text | |
|
图3 基于SCPILR的q轴电流环结构框图 |
| In the text | |
|
图4 谐振控制器随各参数变化的伯德图 |
| In the text | |
|
图5 实验平台 |
| In the text | |
|
图6 基于SCPILR双环控制器方框图 |
| In the text | |
|
图7 速度指令为1 000 r/min及突加负载后, 3种控制器速度跟踪情况 |
| In the text | |
|
图8 3种控制器在突加负载后Id, Iq电流变化情况 |
| In the text | |
|
图9 外加0.1 Ω电阻后3种控制器速度跟踪下电流Id, Iq变化情况 |
| In the text | |
|
图10 在300 r/min、死区时间2 us时3种控制器的实验结果谐波分析 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.