| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 830 - 837 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740830 | |
| Published online | 23 September 2019 | |
Small-Signal Model for Dual Active Bridge Series Resonant DC-DC Converters with Variable-Frequency and Phase-Shift Modulation
变频+移相控制的双有源串联谐振DC-DC变换器的小信号建模
1
School of Automation, Northwestern Polytechnical University, Xi’an 710072, China
2
Department of Information Engineering, University of Padova, Padova 35131, Italy
Received:
27
September
2018
Variable frequency and phase shift modulation can achieve zero-voltage switching (ZVS) of dual active bridge series resonant DC-DC converters(DABSRCs) over a wide operating range so as to effectively improving system efficiency and reliability. In order to study the dynamics of DABSRCs and provide the basis for the closed-loop compensator design, a continuous-time small-signal model is proposed. The generalized average modelling approach is adopted, in which the DC component of the output voltage and the fundamental component of the inductor current and resonant capacitor voltage are selected as the state variables, precisely describing impacts of the resonance on the system dynamics. On the above-mentioned basis, a closed-loop compensator is designed, which achieves the stable operation with the ZVS variable frequency and phase shift modulation. The analysis results are verified by the simulation and experimental results.
摘要
变频+移相双自由度控制技术能够实现双有源串联谐振DC-DC变换器在宽范围工况下的零电压开通,从而有效提升变换器的工作效率和可靠性。提出了变频+移相控制下双有源串联谐振DC-DC变换器的小信号连续域模型,为研究在该控制机制下变换器的动态特性和闭环控制器的设计提供依据。所建立的模型基于广义平均建模法,选取输出电压的直流分量和电感电流、谐振电容电压的基波分量作为状态变量,准确描述了谐振腔对变换器动态特性的影响。在此基础上设计了输出电压闭环调节器,实现了变换器在ZVS变频+移相控制下的稳定运行。理论分析通过Matlab/PLECS仿真和1台800 W原理样机进行了验证。
Key words: DC-DC converters / dual active bridge / series resonant / small-signal modeling / variable frequency / phase shift
关键字 : DC-DC变换器 / 双有源 / 串联谐振 / 小信号建模 / 变频 / 移相
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
双向DC-DC变换器广泛应用于需要功率双向传输的场合中, 如电动汽车、直流微/纳米电网、不间断供电系统等。作为直流总线与储能单元之间的关键接口, 双向DC-DC变换器在系统能量管理和控制中发挥着举足轻重的作用, 受到了国内外学者的广泛关注, 成为一个热门的研究方向。
双有源串联谐振DC-DC变换器(dual active bridge series resonant DC-DC converter, DABSRC)适用于中、高功率双向能量传输的应用场合。其主要特点包括:①电路结构双向对称, 兼备升/降压能力;②谐振电容能够阻隔直流电流分量, 限制异常情况下的故障电流[1];③其固有的谐振特性为变换器的设计和控制提供了更高的灵活性。对于双向DC-DC变换器而言, 特别是在高电压、高功率(>1 kW)应用中, 通常希望有源功率器件尽可能地实现软开关运行。一方面, 软开关可以有效降低开关损耗, 提升变换器的效率。另一方面, 软开关可以抑制开关瞬间的电压变化率, 减小电磁干扰。此外, 软开关还有助于降低功率管在开关瞬间的电压振铃, 提高变换器的可靠性[2]。然而, 受到环境因素和储能单元充放电的影响, 双向DC-DC变换器通常工作于较宽的电压范围和负载范围。这对实现DABSRC的软开关运行提出了挑战。采用定频移相控制的DABSRC在轻载和半载情况下工作在硬开关状态[3]。以降低谐振电流有效值为目标, 采用移相+PWM的控制策略能够有效地改善变换器的工作效率, 但仍无法实现变换器在宽范围条件下的软开关运行[4-5]。为了实现DABSRC在宽电压和宽负载范围工况下的软开关运行, 文献[6]提出了一种变频+移相控制的零电压开关(zero voltage switching, ZVS)控制器, 有效地扩展了变换器的软开关范围。
在实际应用中, 双向DC-DC变换器的输出电压或电流需要通过闭环控制进行动态地调节。对于一个稳定的闭环控制器设计而言, 小信号模型提供了变换器在某一个稳态工作点的动态特性, 是闭环控制器设计的重要依据。目前, DABSRC的小信号建模主要是采用相量变换的方法[7-8]。例如, 文献[8]建立了PWM+移相控制下DABSRC的小信号相量模型。在此基础上, 文献[9]提出了DABSRC的增益可调控制策略来优化变换器的带宽。但是, 上述文献中所提出的模型仅适用于固定开关频率的变换器中, 对变频+移相控制的DABSRC并不适用。
由于双向DC-DC变换器的负载类型可以是恒压型负载也可以是阻性负载。本文的分析讨论主要针对阻性负载, 但对于恒压型负载的情况, 本文所提出的建模方法同样适用。本文基于广义平均建模法[10-11], 考虑谐振电感和谐振电容在开关频率处的动态特性, 针对文献[6]中提出的ZVS控制策略, 建立了变频+移相控制下DABSRC的小信号连续域模型, 并在此基础上设计了闭环控制器。所建立的模型为闭环控制器的设计提供了有效的依据。仿真和实验结果验证了模型的准确性。
1 DABSRC的ZVS变频+移相控制
本文所讨论的DABSRC为非隔离半桥拓扑, 如图 1所示。半桥拓扑通常适用于几百瓦至几千瓦的功率范围[12-13]。该变换器主要由原边半桥电路(功率管S1, S2)、副边半桥电路(功率管S3, S4)和LC串联谐振电路组成。定义原边和副边的直流母线电压分别为Vg和Vo。
在ZVS变频+移相控制中, 开关频率ωs大于谐振频率ωr, 并用于控制功率的传输。同时根据Vg, Vo的状态以及ωs的大小对移相角ϕ进行调整, 从而实现所有功率管的ZVS。图 2给出了原、副边桥臂中点的电压vA, vB, 以及谐振电感电流iL和谐振电容电压vC的波形, 同时还显示了控制变量ωs和ϕ。不考虑导通损耗, DABSRC的输出功率Po可通过基波近似方法得出[6]
式中, 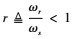 为谐振频率与开关频率之比。M
为谐振频率与开关频率之比。M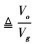 为电压转换比,
为电压转换比,  为特征阻抗。从(1)式中可以看出, 变换器功率传输的方向仅依赖于ϕ的极性, 如果ϕ>0, 则Po>0, 功率从Vg侧传递至Vo侧, 反之, Po < 0, 功率从Vo侧传递至Vg侧。
为特征阻抗。从(1)式中可以看出, 变换器功率传输的方向仅依赖于ϕ的极性, 如果ϕ>0, 则Po>0, 功率从Vg侧传递至Vo侧, 反之, Po < 0, 功率从Vo侧传递至Vg侧。
在降压工作模式(M < 1)下, ZVS变频+移相控制的闭合形式表达式为[6]
式中, u为控制指令, ϕcon和ϕm的表达式为
式中, Jsw为常量, 表示预设的副边开关电流的标幺值(电流基值为Ib=Vg/Z0)。
ZVS变频+移相控制的框图如图 3a)所示。图中, u为控制输入量, 输出电压vo为输出量, 开关频率ωs和移相角ϕ的大小根据(2)式得到。通过该控制策略, 可以实现DABSRC的宽范围ZVS运行。具体分析讨论可参考文献[6]。
在实际应用中, 变换器的输出电压或电流需要通过闭环控制器进行调节。为了确保系统稳定, 通常需要设计一个线性补偿器(如比例-积分(PI)补偿器)来提供足够的稳定裕度, 如图 1所示。
对于DC-DC变换器而言, 小信号模型是补偿器设计的重要依据。本文以输出电压闭环控制为例, 建立ZVS变频+移相控制的DABSRC小信号模型。根据图 3a)所示的控制框图, 考虑稳态工作点处的小信号扰动并进行线性化处理, 可以进一步得出该控制机制下小信号控制输入 到小信号输出电压
到小信号输出电压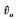 的线性模型框图, 如图 3b)所示。
的线性模型框图, 如图 3b)所示。
图 3b)中传递函数Grωs(s)表示频率比r与开关频率ωs的关系, 可通过r的定义得到, 其表达式为
式中, R表示频率比的稳态值。
传递函数Grϕ(s)表示频率比r到移相角ϕ的关系, 可由(2)式得到
Gωsvo(s)和Gϕvo(s)分别表示开关频率-输出电压和移相角-输出电压的小信号传递函数, 描述了DABSRC的输出电压在稳态工作点相对于开关频率和移相角小信号扰动的动态特性。这2个传递函数的推导是本文的研究重点, 以下将重点展开。
 |
1 非隔离半桥DABSRC及ZVS变频+移相控制框图 |
 |
图2 桥臂中点输出电压和电感电流、谐振电容电压波形, 以及相关的控制变量(DA=DB=50%) |
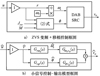 |
3 控制及模型框图 |
2 DABSRC的广义平均模型
假设DABSRC的输入电压Vg保持恒定, 选择电感电流iL、谐振电容电压vc和输出电压vo作为状态变量。根据图 2所示的开关状态, DABSRC的状态方程可以表示为
式中, Rpar表示LC谐振电路和开关管导通电阻的集中等效电阻。s1(t)和s2(t)分别为原、副边半桥电路的开关函数, 根据图 2, 其表达式为
从(7)式中可以看出, 变换器的状态方程是时变、非线性的。为了得到时不变、线性模型, 需要采用状态平均法对(7)式进行平均。广义上讲, 状态平均的基本思路是:在时间间隔t-Ts≤τ≤t, 将状态变量x(τ)用傅里叶级数的形式进行表示, 即
式中, 复数〈x〉k(t)为傅里叶级数中的第k项系数, 它的表达式为
传统的状态平均方法只考虑状态变量的直流分量, 因此仅适用于状态变量纹波较小的场合。然而, 在DABSRC中, 电感电流为交流量, 并且谐振电容电压的交流分量为主要成分。广义平均方法采用更多的傅里叶级数项来表示状态变量, 从而获得更高的准确性。为了准确描述DABSRC的动态特性, 在本文中, 用第k=±1项, 即基波分量来描述状态变量iL和vc, 用k=0项来描述状态变量vo。
广义状态平均法涉及以下2个重要的关系式:
1) 状态变量x的第k项系数的微分
式中,  表示状态变量微分的平均。
表示状态变量微分的平均。
2) 2个状态变量x、y的第k项系数的乘积
由于傅里叶系数中第1项和第-1项是共轭的, 因此, 进一步可得
式中, 下标R和I分别表示复数的实部和虚部。
对状态方程(7)利用关系(10)式和(11)式进行平均, 可得
开关函数s1(τ)和s2(τ)的k=1项傅里叶系数为
综上所述, DABSRC的状态平均方程可表示为
式中
对于给定的稳态控制变量ωs=Ωs, ϕ=Φ, DABSRC的稳态工作点X=[IL1R, IL1I, VC1R, VC1I, Vo]T可以从方程AX+B=0得出。
3 小信号模型
闭环控制器的设计和稳定性分析需要得到小信号控制-输出传递函数, 它反映了变换器在稳态工作点对控制扰动的小信号动态响应。在稳态工作点处, 当开关频率ωs或移相角ϕ出现小扰动时, 即
状态变量x将偏离稳态工作点X, 即
式中, 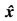 为小信号状态变量。将(21)和(22)代入状态平均方程(20)并进行线性化, 可以得到变频控制下的小信号状态方程为
为小信号状态变量。将(21)和(22)代入状态平均方程(20)并进行线性化, 可以得到变频控制下的小信号状态方程为
式中
同理, 可得移相控制下的小信号状态方程为
式中,  。
。
根据(23)式和(24)式, 可以得到DABSRC在任意稳态工作点处的小信号开关频率-输出电压传递函数Gωsvo(s)和移相角-输出电压传递函数Gϕvo(s)。
4 ZVS变频+移相控制小信号模型
根据图 3b)所示的ZVS变频+移相控制的DABSRC小信号模型框图, 小信号控制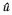 -输出电压
-输出电压 的传递函数可表示为
的传递函数可表示为
若不加入补偿器, 则闭环控制系统的环路增益为传递函数Guvo(s), 其频率特性如图 4所示。变换器的稳态工作点为Vg=200 V, fs=54 kHz, ϕ=45°, RL=45 Ω, Jsw=-0.129。从幅频和相频曲线中可以看出, 在fs-fr=12.7 kHz频率处存在一个谐振点, 并且相位发生了-180°的跳变。由于在谐振点处的幅值大于0 dB, 根据奈奎斯特稳定性判据可知, 在该稳态工作点处变换器是不稳定的。为此必须设计合理的补偿器, 例如一个低增益的PI补偿器, 将谐振点处的幅值抑制到0 dB线以下。同时还可以得出, 受谐振点的影响, DABSRC的带宽通常不高。
需要说明的是, 由于DABSRC的结构对称性, 建立的小信号模型适用于任意方向的功率传输。
 |
图4 不加入补偿器时, 闭环控制系统的环路增益频率特性 |
5 仿真和实验验证
5.1 仿真验证
为了对所建立的小信号模型进行验证, 在Matlab/Simulink/PLECS中建立了DABSRC的仿真模型, 变换器的参数如表 1所示。首先, 对小信号控制-输出电压Guvo(s)的频率特性进行了仿真验证。在仿真过程中, 在稳态控制输入信号U上叠加小信号扰动Δu=Umsin(2πfm), 其中, fm为扰动频率, Um为扰动幅值。通过采集控制指令u和输出电压vo, 并进行快速傅里叶变换分析, 便可得到在给定扰动频率fm下, 输出电压的增益和相位。仿真得到的数据如图 4所示, 可以看出, 仿真结果与所建立的理论模型具有很好的一致性, 验证了模型的准确性。同时, 仿真结果也有效地验证了Guvo(s)中fs-fr频率处谐振点的存在。
为了进一步验证模型在闭环控制器设计方面的有效性, 分别设计了2个PI补偿器, 其参数分别为, 补偿器A:kp=0.2, ki=10;补偿器B:kp=0.1, ki=10, 其中kp为比例系数, ki为积分系数。图 5给出了加入这2个补偿器之后的环路增益在(fs-fr)附近的幅频特性。
从图中可以看出, 使用补偿器A(kp=0.2, ki=10)的环路增益在谐振点处超过了0 dB线, 而使用补偿器B(kp=0.1, ki=10)的环路增益在谐振点处小于0 dB。图 6分别给出了在电压闭环控制下, 输出电压vo和电感电流iL的仿真波形。在仿真中, 输入电压Vg=200 V, 输出电压参考为140 V, 负载电阻RL=45 Ω。仿真结果表明, 当kp=0.1时, 变换器运行稳定。相比较而言, 当kp=0.2时, 输出电压和电感电流出现了明显振荡, 变换器不稳定。该仿真结果与理论分析一致。
采用补偿器B, 图 7为正、反向功率传输时变换器的仿真波形。功率正向传输时, Vg侧接200 V电源, Vo侧接45 Ω电阻负载; 功率反向传输时, Vg侧接45 Ω电阻负载, Vo侧接200 V电源。参考电压设置为140 V。可以看出, 同一组补偿器参数适用于不同的功率流向, 从而验证了建立的小信号模型可用于任意功率流向的动态性能分析。
双有源串联谐振变换器参数
 |
5 加入PI补偿器之后的环路增益幅频曲线 |
 |
图6 闭环控制下, 输出电压和电感电流的仿真波形 |
 |
7 闭环控制下, 功率正向和反向传输时的稳态波形 |
5.2 实验验证
搭建了一台最大输出功率为800 W的非隔离半桥DABSRC原理样机, 样机参数与仿真模型一致(参见表 1), 如图 8所示。样机的控制算法通过微控制器TMS320F28377S实现, 输出电压vo的采样与开关周期同步, 电压闭环的控制周期为20 μs。在实际应用中, PI补偿器的设计要使系统具有足够的裕度, 以克服参数的变化、输入/输出电压范围和负载变化的影响。因此, 在实验中, 所设计的PI补偿器参数为kp=0.03, ki=10, 具备15 dB的幅值裕度和75°的相角裕度, 变换器的带宽为200 Hz。
采用所设计的PI补偿器, 对ZVS变频+移相控制的DABSRC进行闭环控制。图 9给出了输入电压200 V, 输出电压140 V, 突加负载(217~436 W)和突卸负载(436~217 W)的实验波形。负载的突变通过使用机械开关旁路负载电阻实现。此外, 图 9中还给出了频率比r和移相角ϕ的动态变化过程。从实验结果可以看出, 当负载剧烈变化时, 变换器的控制参数平滑调节, 变换器运行稳定, 并且表现出良好的动态特性。
图 10给出了DABSRC在不同负载下的稳态实验波形。可以看出, 在功管开通时刻, 功率管的漏源电流均小于0, 表明所有功率管均实现ZVS运行。从而进一步证明, 依据所提出的小信号模型所设计的闭环PI补偿器与ZVS控制器匹配良好, 变换器工作稳定, 具有很好的稳态特性。
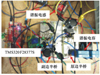 |
图8 DABSRC原理样机图片 |
 |
9 负载变化时, 输出电压、电感电流以及控制变量的动态实验波形 |
 |
图10 输出电压、电感电流和桥臂中点输出电压的稳态实验波形 |
6 结论
本文针对双有源串联谐振DC-DC变换器, 基于广义平均建模方法, 提出了在ZVS变频+移相控制下变换器的小信号模型, 为闭环控制系统的环路设计提供了有力依据。所建立的模型为5阶系统, 准确反映了谐振电感和谐振电容的基波分量对变换器动态特性的影响。理论分析表明, 由于DABSRC频率响应中谐振峰值的存在, 闭环控制系统的幅值裕度是影响系统稳定性和限制带宽的主要因素。根据所提出的模型, 设计了DABSRC的输出电压闭环控制器, 实现了变换器的稳定可靠运行, 并使其具有良好的动态和稳态性能。仿真和实验结果均验证了模型的准确性和有效性。
References
- Lenke R, Mura F, Doncker R W D. Comparison of Non-Resonant and Super-Resonant Dual-Active ZVS-Operated High-Power DC-DC Converters[C]//13th European Conference on Power Electronics and Applications, 2009 [Google Scholar]
- Chung H, Hui S Y R, Tse K K. Reduction of Power Converter EMI Emission Using Soft-Switching Technique[J]. IEEE Trans on Electromagnetic Compatibility, 1998, 40(3): 282–287 [Article] [CrossRef] [Google Scholar]
- Li X, Bhat A K S. Analysis and Design of High-Frequency Isolated Dual-Bridge Series Resonant DC/DC Converter[J]. IEEE Trans Power Electron, 2010, 25(4): 850–862 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Corradini L, Seltzer D, Bloomquist D, et al. Minimum Current Operation of Bidirectional Dual-Bridge Series Resonant DC/DC Converters[J]. IEEE Trans on Power Electronics, 2012, 27(7): 3266–3276 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Hu S, Li X, Bhat A K S. Operation of a Bidirectional Series-Resonant Converter with Minimized Tank Current and Wide ZVS Range[J]. IEEE Trans on Power Electronics, 2019, 34(1): 904–915 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Han W, Corradini L. Wide-Range ZVS Control Technique for Bidirectional Dual-Bridge Series Resonant DC-DC Converters[J]. IEEE Trans on Power Electronics, 2019, 34(10): 10256–10269 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Rim C T, Cho G H. Phasor Transformation and Its Application to the DC/AC Analyses of Frequency Phase-Controlled Series Resonant Converters(SRC)[J]. IEEE Trans on Power Electronics, 1990, 5(2): 201–211 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Seltzer D, Corradini L, Bloomquist D, et al. Small Signal Phasor Modeling of Dual Active Bridge Series Resonant DC/DC Converters with Multi-Angle Phase Shift Modulation[C]//2011 IEEE Energy Conversion Congress and Exposition, 2011 [Article] [Google Scholar]
- Seltzer D, Bloomquist D, Zane R, et al. Gain-Scheduled Control of Multi Angle Phase Shift Modulated Dual Active Bridge Series Resonant DC/DC Converters[C]//2012 IEEE 13th Workshop on Control and Modeling for Power Electronics, 2012: 1–7 [Article] [Google Scholar]
- Sanders S R, Noworolski J M, Liu X Z, et al. Generalized Averaging Method for Power Conversion Circuits[J]. IEEE Trans on Power Electronics, 1991, 6(2): 251–259 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Qin H, Kimball J W. Generalized Average Modeling of Dual Active Bridge DC-DC Converter[J]. IEEE Trans on Power Electronics, 2012, 27(4): 2078–2084 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Erickson R W, Maksimoviĝ D. Fundamentals of Power Electronics[M]. 2nd ed. Springer, 2001 [CrossRef] [Google Scholar]
- Xiangli K, Li S, Smedley K M. Decoupled PWM Plus Phase-Shift Control for a Dual-Half-Bridge Bidirectional DC-DC Converter[J]. IEEE Trans on Power Electronics, 2018, 33(8): 7203–7213 10.1109/TPEL.2017.2758398 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
1 非隔离半桥DABSRC及ZVS变频+移相控制框图 |
| In the text | |
 |
图2 桥臂中点输出电压和电感电流、谐振电容电压波形, 以及相关的控制变量(DA=DB=50%) |
| In the text | |
 |
3 控制及模型框图 |
| In the text | |
 |
图4 不加入补偿器时, 闭环控制系统的环路增益频率特性 |
| In the text | |
 |
5 加入PI补偿器之后的环路增益幅频曲线 |
| In the text | |
 |
图6 闭环控制下, 输出电压和电感电流的仿真波形 |
| In the text | |
 |
7 闭环控制下, 功率正向和反向传输时的稳态波形 |
| In the text | |
 |
图8 DABSRC原理样机图片 |
| In the text | |
 |
9 负载变化时, 输出电压、电感电流以及控制变量的动态实验波形 |
| In the text | |
 |
图10 输出电压、电感电流和桥臂中点输出电压的稳态实验波形 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


