| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 838 - 845 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740838 | |
| Published online | 23 September 2019 | |
Estimation for Two-Dimensional Incoherently Distributed Source in Double L-Shape Arrays
基于双L型阵列的二维非相干分布源参数估计
1
School of Automation, Northwestern Polytechnical University, Xi’an 710072, China
2
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
Received:
10
August
2018
Distributed sources can be regarded as an assembly of point sources within a spatial distribution. In this paper, we explore the estimation of the two-dimensional incoherently distributed sources using double L-shape arrays. The rotational invariance properties of the nominal elevation and nominal elevation are firstly obtained by taking first-order Taylor series expansions with regard to the generalized steering vectors of two pairs of parallel subarrays. The rotation operators can be solved based on signal subspace. Then the nominal elevation and nominal elevation can be obtained from parameters matching method. Estimation of direction of arrival can be used in multi-source scenario and needn't peak-finding search. Lastly the angular spreads can be solved through two-dimensional Capon search based on nominal angles. The simulation experiments show that the proposed method has good performance on the estimation of two-dimensional incoherently distributed sources. Investigating different experimental conditions, sources with different angular spreads, simulations are conducted to validate better estimation accuracy of the proposed method.
摘要
分布源信号可以看作点源信号在一定空间范围内的聚集。研究二维非相干分布源的参数估计问题，提出一种基于双L型阵列结构的分布源参数估计方法。通过一阶泰勒展开推导出平行阵列广义方向矢量关于中心方位角和中心俯仰角的旋转不变关系，在此基础上利用接收矢量协方差矩阵的信号子空间得出旋转算子，依据参数配对方法解算出中心方位角和中心俯仰角，二维波达方向的估计不需要谱峰搜索，适用于角功率函数未知和多个分布源的情景。最后通过二维Capon谱峰搜索确定角度扩展参数。通过仿真考察实验条件、扩展角度对估计结果的影响，实验表明所提算法具有良好估计性能。
Key words: direction of arrival / incoherently distributed sources / generalized steering vectors / double L-shape arrays
关键字 : 波达方向 / 非相干分布源 / 广义方向矢量 / 双L型阵列
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
在阵列信号处理中，传统的信源参数估计算法以点目标模型为基础。当目标的空间散射特性可以忽略、目标与接收阵列之间为直线路径, 点目标模型可以简化计算，有效进行参数估计。在无线通信领域，目标与接收阵列周围存在较多障碍物，目标到达阵列通过多条路径传播；在水下声呐工作环境中, 信号传播存在海底与海面的反射路径，随着目标与接收阵列之间的距离缩短，目标反射信号的各个部位都可以看作散射体，此时信源的参数估计就必须要考虑目标的空间分布特征。当信源的空间散射特性不能被忽略时，点目标模型不能有效描述信号源特征，基于点目标模型的信源参数估计也会存在较大误差。
为了克服点目标模型的局限，学者们提出了分布源模型[1]。分布源信号可以看作点源信号在一定空间分布内的聚集。分布源依据其散射单元的时间相关性主要分为非相干分布源和相干分布源。非相干分布源和相干分布源的空间分布特征分别用角功率密度函数和角信号分布函数来描述。根据分布源的空间分布特点，角功率密度函数或者角信号分布函数可以表示为多种分布函数，通常有高斯分布、均匀分布和非对称分布[2]。针对分布源模型，学者们提出多种参数估计算法，主要有子空间类算法如DSPE[1]和DSPARE[3]、协方差匹配算法[4-5]、极大似然估计算法[6-7]和波束形成算法[8]。以上参数估计算法假设分布源与接收阵列处于同一平面即采用一维分布源模型，分布源的角功率密度函数或者角信号分布函数用波达方向或称为中心角以及角度扩展2个参数来描述。分布源与接收阵列处于不同平面即二维分布源模型更具有一般性，此时分布源用波达方向包括中心方位角和中心俯仰角、角度扩展包括方位角扩展和俯仰角扩展来描述，复杂程度显著增加。
对于二维相干分布源模型，代表性的成果为国内学者利用广义方向矢量的泰勒近似得出信号子空间的旋转不变关系，针对不同的阵列结构提出多种参数估计算法[9-12]。对于二维非相干分布源模型国内外研究较少。文献[13]提出二维协方差匹配算法，该方法采用四维非线性优化求解二维中心角和角度扩展，计算量巨大。文献[14]利用均匀平面阵提出一种类ESPRIT算法，该算法针对二维非相干分布源求解中心角而没有涉及角度扩展参数。文献[15]利用双平行线阵、三平行线阵和L型阵对分布源的低复杂度参数估计做了系统的研究，并针对双平行阵列提出一种非相干分布源中心角估计算法，首先利用旋转不变关系计算出中心俯仰角，利用一维Capon谱峰搜索来计算中心方位角，再通过二维Capon谱峰搜索来得到扩展参数，计算复杂度也较高。
本文研究二维非相干分布源模型的参数估计。首先针对双L型阵列结构特点推导出阵列广义方向矢量关于中心方位角和中心俯仰角的旋转不变关系，在此基础上利用接收矢量协方差矩阵的信号子空间解算出旋转算子，依据Capon估计准则提出一种参数配对方法，从而得出中心俯仰角和中心方位角。本文二维波达方向的估计不需要谱峰搜索，适用于角功率函数未知和多个分布源的情景。在中心角已知的基础上，通过Capon谱峰搜索确定扩展参数。
1 二维非相干分布源模型
双L型阵列结构如图 1所示。阵列由位于xoz平面的两对平行线阵X1和X2、Z1和Z2组成, 其中X1和Z1分别位于x轴和z轴, 共有位于原点的第一个阵元。每对平行线阵间的间隔为δ, 每条线阵有间距为d的M个阵元。
假设远场有k个窄带二维分布源以中心角为(θi, ϕi) (i=1, 2, …, k)入射到阵列。其中θi为第i个分布源的中心方位角, ϕi为第i个分布源中心俯仰角, θi∈[0, π], ϕi∈[0, π]。则阵列的接收矢量可以表示为
式中, nxm(t)与nzm(t)为与信号不相关的加性高斯白噪声, 噪声功率为σn2。m=1, 2。x1(t)和x2(t)分别表示阵列X1和X2的接收矢量; z1(t)和z2(t)分别为阵列Z1和Z2的接收矢量; α1(θ, ϕ)和α2(θ, ϕ)分别表示点源信号在X1和X2的方向矢量; β1(θ, ϕ)和β2(θ, ϕ)分别表示点源信号在Z1和Z2的方向矢量。
si(θ, ϕ, t)是第i个分布源的角信号密度函数, si(θ, ϕ, t)为一随机过程, 反应第i个分布源在t时刻不同角度上散射分量的贡献。非相干分布源模型假设同一分布源不同角度的散射完全不相关, 则存在以下关系
式中，σi2是第i个分布源的功率, pi(θ, ϕ, t)是归一化的角功率密度函数满足以下关系
 |
图1
双L型阵列结构 |
2 算法原理
2.1 广义方向矢量的旋转不变关系
将阵列X1和X2的方向矢量在(θi, ϕi)处做一阶泰勒级数展开如下
式中, [·]′θ和[·]′ϕ分别表示函数在(θi, ϕi)处关于θ和ϕ的一阶偏导数。
如果δ/λ≪1, [α2(θi, ϕi]′ϕ的第二项可以忽略不计则存在以下近似关系
定义广义信源矢量s=[s1, s2, s3]H
式中
可以证明, 存在以下关系[15]
式中
由于不同的分布源是不相关的, 则
定义X1阵列的广义方向矢量[A11, A12, A13]为
则X1阵列的接收矢量可以表示为
定义X2阵列的广义方向矢量[A21, A22, A23]为
则X2阵列的接收矢量可以表示为
根据(8)~(9)式可以得到如下关系
式中
将阵列Z1和Z2的方向矢量在(θi, ϕi)做一阶泰勒级数展开如下
式中
如果d/λ≪1, 则(25)式右端及(26)式第二项可以忽略不计则有以下关系
定义Z1阵列方向矢量[B11, B12]
则Z1阵列的接收矢量可以表示为
定义Z2阵列方向矢量[B11, B12]为
Z2阵列的接收矢量可以表示为
根据(27)式得出以下关系
2.2 中心角参数估计
将X1和X2阵列的接收矢量合并如下
式中
X1和X2阵列的接收矢量协方差矩阵可以表示为
在小角度扩展的条件下, Mθi和Mϕi都是小于1的数, 对协方差矩阵Rx12进行特征分解, 得到协方差矩阵最大的k个特征值对应的特征向量构成的子空间Ex。Ex子空间与Ax1张成的子空间相同, 则存在一个k×k非奇异矩阵T满足以下关系
令Ex1和Ex2分别为Ex的上k行和下k行则有
可以得到以下关系
定义Ωx=T-1ΦT则
其中(·)+表示伪逆算子, 从而可以求解出分布源的中心俯仰角
式中, ηi为Ωx第i个特征值。angle(·)表示取复变量的辐角。
将Z1和Z2阵列的接收矢量合并如下
式中
Z1和Z2阵列的接收矢量协方差矩阵可以表示为
对协方差矩阵Rz12进行特征分解, 得到与协方差矩阵最大的k个特征值对应的特征向量构成的子空间Ez。Ez子空间与Bz1张成的子空间相同, 则存在一个k×k个的非奇异矩阵Q满足以下关系
令Ez1和Ez2分别为Ez的上k行和下k行则有以下关系
进一步可以得到
定义Ωz=Q-1ΨQ则
进而得出
式中，μi为Ωz第i个特征值。
2.3 角度配对
考虑平行阵列X1和X2的广义方向矢量[Ax1, Ax2, Ax3], Capon估计准则可以表示为
(54) 式可以通过拉格朗日函数进行求解, 得出Capon代价函数为
式中，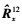
为平行阵列X1和X2的协方差矩阵估计值
角度配对的步骤可以归纳如下
1) 从集合{ϕ1, ϕ2, …, ϕk}任选一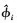
, 遍历集合{angle(μ1), angle(μ2), …, angle(μk)}依据(53)式求解出k个与
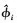的角度配对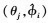
(j=1, 2, …, k)。
2)将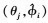
(j=1, 2, …, k)带入(55)式选择使L(θ, ϕ)最大的θj为
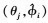的配对, 记为
。
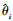3) 将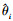
从集合{ϕ1, ϕ2, …, ϕk}剔除, 同时将
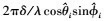从集合{angle(μ1), angle(μ2), …, angle(μk)}剔除, 重复步骤1~步骤2。
经过(k+2)(k-1)/2次计算就可以配对出所有的中心方位角和中心俯仰角。
2.4 扩展参数估计
考虑阵列X1, 信号协方差矩阵可以表示为
对于高斯分布
式中，ui=[θi, ϕi, σθi, σϕi], 假设d/λ=0.5且在小角度扩展的前提下有
式中，[·]lh表示矩阵第l行h列的元素。
对于均匀分布
方位角扩展和俯仰角扩展可以采用Capon估计准则通过二维谱峰搜索得出
式中，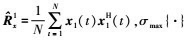
表示矩阵的最大特征值。
2.5 算法步骤和复杂度分析
根据上述分析, 本文算法步骤归纳如下
1) 计算协方差矩阵的估计值
。
2) 对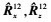
进行特征分解得出子空间Ex和Ez, 根据(42)、(52)式计算得出Ωx和Ωz。
3) 对Ωx和Ωz进行特征分解得出特征值ηi和μi。
4) 依据参数配对方法确定中心角度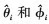
。
5) 依据(59)式、(60)式或者(62)式、(63)式确定R(θ, ϕ; ui), 根据(64)式得出扩展参数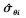
和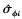
。
本文算法求解中心角复杂度主要包括三部分:①计算协方差矩阵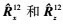
, 复杂度为O(NM2); ②特征分解
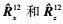, 复杂度为O(M3); ③求解及特征分解Ωx和Ωz, 复杂度为O(k3); 文献[15]提出的双平行线的估计方法复杂度包括三部分:①计算协方差矩阵
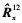复杂度为O(NM2); ②特征分解
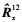复杂度为O(M3)。③一维搜索复杂度为O(kLθM2), 其中Lθ为方位角的搜索点数。显然, 本文提出的算法复杂度低于文献[15]。在得出中心角的基础上求解扩展参数的计算复杂度主要包括两部分:①协方差矩阵
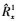求逆, 复杂度为o(M3)；②通过二维搜索得出扩展参数, 复杂度为o(kM3LσθLσϕ), Lσθ和Lσϕ为方位角扩展和俯仰角扩展搜索的点数。
3 仿真实验与分析
本文通过3个仿真实验来验证算法的有效性, 考虑阵列结构如图 1所示, 每条线阵阵元数M=8, 阵元间距d=λ/2, 平行阵列间隔δ=λ/10。
中心角的均方根误差的Ga定义为
Mc为蒙特卡罗仿真次数,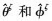 
表示第ζ次蒙特卡罗仿真实验估计的中心方位角和中心俯仰角。角度扩展的均方根误差Gs定义为
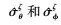表示第ζ次蒙特卡罗仿真实验估计的方位角扩展和俯仰角扩展。
实验1 考察信噪比和快拍数对实验的影响。假设目标参数为[30°, 45°, 2°, 3°]的二维非相干高斯分布源信号。实验采用100次独立的蒙特卡罗仿真验证完成。图 2反应快拍数等于200时中心角均方根误差和角度扩展均方根误差随信噪比从0~30 dB的变化情况。图 3反应信噪比等于20 dB时中心角均方根误差和角度扩展均方根误差随快拍数从20~200的变化情况。为了验证算法的性能, 图中还给出采用文献[15]的方法利用双平行线X1和X2得出的结果。可以看到随着快拍数和信噪比的提高算法估计精度不断提高, 本文算法在相同实验条件下的估计精度优于文献[15]提出的算法。
实验2 考察角度扩展的变化对中心角估计的影响。针对中心角度为(60°, 35°)一个非相干二维分布源, 分别考虑2种角功率密度函数:高斯分布和均匀分布。考察方位角扩展和俯仰角扩展同时从0°变化到10°时中心角均方根误差的变化。实验采用100次独立的蒙特卡罗仿真验证完成, 信噪比为20 dB, 快拍数为200。图 4表明对于角功率密度函数为高斯分布的分布源, 随着角度扩展的增加估计精度会降低, 角度扩展为5°时, 中心角均方根误差为0.03;角度扩展达为10°时误差为0.4。对于均匀分布的分布源, 随着角度扩展的增加估计精度同样降低, 角度扩展为5°时, 中心角均方误差为0.04, 10°时误差为0.7。实验表明随着角度扩展的增加估计性能会下降, 但是在10°以内仍具有满意的估计效果。本文提出的算法中心角度的估计在小角度扩展的情况下具有鲁棒性。
实验3 考察算法对多个分布源的估计能力。考虑参数为[25°, 70°, 2°, 3°], [35°, 40°, 3.5°, 4.5°]和[55°, 80°, 1.5°, 2°]的3个均匀非相干二维分布源，信噪比为20 dB, 快拍数为200。实验采用100次独立的蒙特卡罗仿真完成。图 5和图 6分别给出3个均匀分布源中心角和角度扩展估的结果。实验结果表明本文算法可以有效估计多个分布源的参数。
需要说明的是本文旋转不变关系的得出是建立在假设平行线阵间隔很小, 与信号波长之比远小于1即δ/λ≪1的条件之上。在工程实际中如果阵元间距很小, 一方面阵元间的互耦效应将不能被忽略; 另一方面, 阵元的安装误差也会影响估计效果, 所以在一些高频信号领域如移动通信很难适用。但是在低频水下探测领域, 声纳的探测频率可以降到100 Hz, 这意味着信号波长可以达到14.5 m; 在这种情况下, δ/λ实际上可以达到很小的值, 完全可以满足假设条件。
 |
图2
分布源参数均方根误差随着信噪比的变化 |
 |
图3
分布源参数均方根误差随着快拍数的变化 |
 |
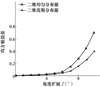图4
中心角均方根误差随着角度扩展的变化 |
 |
图5
3个分布源中心角估计的结果 |
 |
图6
3个分布源扩展参数估计的结果 |
4 结论
本文利用双L型阵列，提出一种二维非相干分布源参数估计方法。首先推导出广义方向矢量关于中心角的在双L型阵列下的旋转不变关系，在协方差矩阵特征分解的基础上计算得出旋转算子，参数配对后解出中心角。在中心角已知的基础上通过二维搜索得出角度扩展参数。仿真结果表明，在平行线阵间隔很小的条件下，本文提出的参数估计方法具有良好的估计性能。
References
- Xiong W, José P, Sylvie M. Performance Analysis of Distributed Source Parameter Estimator(DSPE) in the Presence of Modeling Errors Due to the Spatial Distributions of Sources[J]. Signal Processing, 2018, 143: 146–151 [Article] [CrossRef] [Google Scholar]
- Wu T, Deng Z H, Gu Q Y. Estimation for Two-Dimensional Nonsymmetric Coherently Distributed Source in L-Shaped Arrays[EB/OL]. (2018-09-03)[2019-04-21]. https://www.hindawi.com/journals/ijap/2018/5247919/. [Google Scholar]
- Meng Y, Stoica P. Estimation of Direction of Arrival of Spatially Dispersed Signals in Array Processing[J]. IEE Proceedings-Radar Sonar and Navigation, 1995, 143(1): 1–9 [CrossRef] [Google Scholar]
- Besson O, Stoica P. Decoupled Estimation of DOA and Angular Spread for a Spatially Distributed Source[J]. IEEE Trans on Signal Processing, 2000, 48(7): 1872–1882 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Shahbazpanahi S, Valaee S, Gershman A B. A Covariance Fitting Approach to Parametric Localization of Multiple Incoherently Distributed Sources[J]. IEEE Trans on Signal Processing, 2004, 32(3): 592–600 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Raich R, Goldberg J, Messer H. Bearing Estimation for a Distributed Source:Modeling, Inherent Accuracy Limitations and Algorithms[J]. IEEE Trans on Signal Processing, 2000, 48(2): 429–441 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Besson O, Vincent F, Stoica P, et al. Approximate Maximum Likelihood Estimators for Array Processing in Multiplicative Noise Environments[J]. IEEE Trans on Signal Processing, 2000, 48(9): 2506–2518 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Zoubir A, Wang Y. Robust Generalised Capon Algorithm for Estimating the Angular Parameters of Multiple Incoherently Distributed Sources[J]. IET Signal Processing, 2008, 2(2): 163–168 [Article] [CrossRef] [Google Scholar]
- Dai Z, Cui W, Ba B. Two-Dimensional DOA Estimation for Coherently Distributed Sources with Symmetric Properties in Crossed Arrays[EB/OL]. (2017-07-06)[2019-03-01]. https://www.mdpi.com/1424-8220/17/6/1300 [Google Scholar]
- Wen C, Shi G, Xie X. Estimation of Directions of Arrival of Multiple Distributed Sources for Nested Array[J]. Signal Processing, 2017, 130: 315–322 [Article] [CrossRef] [Google Scholar]
- Yang X, Zheng Z, Chi C K. Low-Complexity 2D Parameter Estimation of Coherently Distributed Noncircular Signals Using Modified Propagator[J]. Multidimensional Systems & Signal Processing, 2017, 28(2): 407–426 [Article] [CrossRef] [Google Scholar]
- Wan L, Han G, Jiang J. A DOA Estimation Approach for Transmission Performance Guarantee in D2D Communication[J]. Mobile Networks & Applications, 2017, 22(6): 998–1009 [Article] [CrossRef] [Google Scholar]
- Boujemâa H. Extension of COMET Algorithm to Multiple Diffuse Source Localization in Azimuth and Elevation[J]. Trans on Emerging Telecommunications Technologies, 2005, 16(6): 557–566 [Article] [CrossRef] [Google Scholar]
- Wu T, Deng Z H, Li Y W. Two-Dimensional DOA Estimation for Incoherently Distributed Sources with Uniform Rectangular Arrays[EB/OL]. (2018-10-23)[2019-04-12]. https://www.mdpi.com/1424-8220/18/11/3600 [Google Scholar]
- Zheng Zhi. Study on Low-Complexity Parameter Estimation Method for Distributed Sources[D]. Chengdu, University of Electronic Science and Technology of China, 2011(in Chinese) (In chinese) [Google Scholar]
All Figures
|
图1
双L型阵列结构 |
| In the text | |
|
图2
分布源参数均方根误差随着信噪比的变化 |
| In the text | |
|
图3
分布源参数均方根误差随着快拍数的变化 |
| In the text | |
|
图4
中心角均方根误差随着角度扩展的变化 |
| In the text | |
|
图5
3个分布源中心角估计的结果 |
| In the text | |
|
图6
3个分布源扩展参数估计的结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.