EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 42 / No 5 (October 2024) JNWPU, 42 5 (2024) 903-911 Full HTML
Open Access
Issue
JNWPU
Volume 42, Number 5, October 2024
Page(s) 903 - 911
DOI https://doi.org/10.1051/jnwpu/20244250903
Published online 06 December 2024

© 2024 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

近期，6G及未来通信系统引发了人们的关注，其中最受人关注的是将感知功能融入通信系统，形成融合感知与通信(integrated sensing and communication, ISAC)的一体化系统[1]。ISAC赋予通信基础设施感知能力，使其能够共享资源并在感知频段进行通信。实现这一愿景需要精心设计传输波形、接收信号后处理和多输入多输出(multi-input multi-output, MIMO)波束赋形等关键技术[2–3]。尽管ISAC在单个基站上的应用备受关注，但在实际应用中，多个ISAC基站可能会在相同的地理区域、频段和时间内工作，从而可能产生相互干扰。这激发了对这些分布式节点之间协调的研究，以提高通信和传感性能。这些问题最终引出了一项新的研究——去蜂窝MIMO-ISAC系统的探讨[4]。在去蜂窝MIMO-ISAC系统中，中央处理单元(CPU)通过前向/回程链路与接入点(AP)相连接，系统引入了以用户为核心的服务构架。通过配置单根或多根天线，系统实现了覆盖范围更广阔的连续覆盖，从而跳出传统蜂窝覆盖的思维定式。这一创新性架构克服了蜂窝边界和频率资源限制等局限性。

然而，随着ISAC应用场景的不断扩展，为了满足其对高容量、低延迟和可靠性的需求，面临的新挑战也逐渐显现出来[5]。尤其是在传统频段广泛应用情况下，通信频谱资源日益匮乏，导致通信系统面临严重的拥挤问题[6]。为了克服频谱资源匮乏带来的难题，研究人员和工程师们将目光聚焦在毫米波技术上，将其视为5G移动通信的重要解决方案[7]。毫米波技术工作频段位于30 GHz~300 GHz之间，其在5G系统中的应用被认为具有巨大的潜力，主要优势在于其连续大带宽特性[8]。相比传统频段，毫米波频段的大带宽使得通信系统能够利用更多的频谱资源，从而显著缓解频谱拥堵问题。这为ISAC应用的感知和通信性能提供了更大的提升空间。

然而，将毫米波技术应用于通感一体化场景时，仍然会面临着分布式基站之间互相干扰的问题。随着ISAC系统在地理区域、频段和时间上的多个基站同时工作，相互之间的干扰可能会影响整个系统性能。因此，探讨将毫米波技术应用于去蜂窝MIMO-ISAC系统成为一个值得研究的话题。在采用毫米波通信时，由于其传播路径损耗较大，传统方式通常采用MIMO预编码技术，然而这种方式的复杂性较高。因此，本文引入一种混合模拟/数字(hybrid analog/digital, HAD)波束赋形结构[9–10]。这种HAD波束赋形设计能够在使用较少射频链路的情况下，实现接近全数字预编码的系统性能。同时，该设计还能确保毫米波通信的传播覆盖范围，从而进一步提升系统的实用性。HAD结构发射端具有Nt个天线配置, 用于向接收端传输Ns个数据流, 接收端配备Nr个天线。为了实现多数据流通信, 在发射端中还配备了NtRF个发射链, 使得发射端硬件能够充分利用NtRF个发射链去应用NtRF×Ns个基带预编码器FBB, 随后使用Nt×NtRF个模拟电路预编码器FRF, 需要注意，此硬件架构特点在于Ns≤NtRF≤Nt的关系。

1 系统模型

考虑一个去蜂窝MIMO-ISAC系统, 该系统由M个接入点(AP)和U个单天线通信用户(UE)组成。每个AP在传输和接收端都配备了Nt和Nr个天线, 使其能够支持Ns条数据流, 并应用混合波束赋形功能。所有AP都连接到中央处理单元, 以实现联合设计和处理。在传感和通信目的下, 所有AP被假定为完全同步。

1.1 信号模型

在本小节中对下行传输的感知和通信信号模型进行了定义。在此模型中, AP联合传输U个通信流和Q个感知流。将通信流和感知流的第i个数据符号分别表示为: {su[i]}u∈U和{sq[i]}q∈Q, 其中{su[i]}u∈U代表第m个AP发送的第i个通信流数据符号; 而{sq[i]}q∈Q则表示第m个AP发送的第i个感知流数据符号。如果xm[i]∈CNt×1表示第m个AP发送的第i个数据流符号, 则可以写出

式中：sj[i]∈CNs×1表示第j个数据流发送的第i个符号; fmp∈CNt×1为波束赋形向量; J=U∪Q={1, …, j}为数据流的整体集合, 且J=U+Q。

在去蜂窝MIMO-ISAC混合波束赋形系统中, 根据AP端的发射信号, 可以得到UE端的接收信号y∈CNr×1被表示为

式中, ρ代表接收功率; H∈CNr×Nt是信道矩阵, 满足E[‖H‖F2]=NtNr; n~CN(0, σn2)是信号噪声向量。为了不失一般性并综合考虑混合波束赋形矩阵的情况, 可以自然地将(1)式扩展为x=FRFFBBs。其中, FRF∈CNt×NtRF表示模拟波束赋形矩阵; FBB∈CNtRF×Ns为数字波束赋形矩阵; s为sj[i]的简单改写形式, 且满足E[ss*]=INs。所以(2)式可以被重写为

在无线通信系统中, UE端在接收信号后需要经历一系列的处理步骤以获取可用的接收信号。其中, RF数据链和基带合并器是2个至关重要的组件。通过这2个组件进行处理后, 获得的信号表达如下

式中：WBB*∈CNr×NrRF为数字域合并矩阵；WRF*∈CNrRF×Ns为模拟域合并矩阵。在对通信模型的性能进行评估时, 频谱效率是一个重要的考量指标。频谱效率是指在数据流通过信道传输时所实现的数据传输速率与单位频谱带宽之比。频谱效率的计算公式如下[11]

式中：Rn=σn2WBB*WRF*WRFWBB为噪声方差矩阵。

本文的研究专注于毫米波频段通信系统的设计, 其中采用了Saleh-Valenzuela模型来对信道进行建模[12–13]。在这个背景下, 信道模型H∈CNr×Nt用于表征信号的传输特性。

式中：αl为第l条路径的增益系数; L为去蜂窝MIMO-ISAC系统中总的路径数; θrl∈[0, 2π)和θtl∈[0, 2π)分别为信号的到达角(angle-of-arrival, AOA)和发射角(angle of departure, AOD); at(θtl)和ar(θrl)分别为发送天线和接收天线的阵列响应矢量。在本系统中收发端天线采用均匀线性阵列(uniform linear array, ULA), 其阵列响应矢量表示为[14]

式中: d为天线间距; λ为信号波长; N表示天线数量。

1.2 感知模型

在通感一体化模型中, 雷达探测模型通常用于实现系统的感知功能。去蜂窝MIMO-ISAC系统的雷达发射波形图可由下列公式描述[15]

式中, R∈CNt×Nt为发射信号的波形协方差矩阵, 可以表示为

根据(8)式, 可以推断设计雷达的方向图等效于设计对应的协方差矩阵。假设在角度{φ1, φ2, …, φK}上存在K个目标, 根据(6)式, 信道矩阵表示为L个不同发射角和到达角的散射路径总和。信道的前K个散射路径即对应雷达感知的K个目标路径。因此, 信道的前K个路径的发射角应该与雷达感知到的发射角一致, 即{φ1, φ2, …, φK}。剩下的L-K个发射角和L个到达角则服从在[-π/2, π/2]范围内均匀分布的情况。

1.3 优化目标

本文旨在设计一种模拟和数字混合波束形成器, 用于在AP和UE之间建立高质量的通信链路, 并且能获得实现优化的雷达波束图。该设计旨在实现2个关键目标: 一方面确保通信用户之间的通信质量, 另一方面获取目标的位置信息以实现探测和追踪能力。因此, 对于混合波束赋形矩阵FRFFBB的设计, 应综合考虑通信全数字波束赋形矩阵Fcom和雷达波束赋形矩阵Frad的特点。这样一来, 在满足去蜂窝场景中维持通信性能的前提下, 系统还能够像雷达系统一样实现波束追踪的能力, 从而实现对目标的精确探测和跟踪。

由于FRFFBB与Fcom的维度均为Nt×Ns, 而Frad的维度为Nt×K, 在联合通感性能中, 感知与雷达矩阵维度不一样可能导致后续算法复杂度提高, 为了保证矩阵维度一致, 本文引入辅助矩阵Faux∈CK×Ns, 其构造方法将在2.3节给出。由此可以得到去蜂窝MIMO-ISAC通感混合波束优化问题

式中：η∈[0, 1]代表权重因子, 它在决定雷达和通信性能权重方面起着重要作用; Ap表示部分连接模拟波束形成器的可行集合, 该集合将恒模约束施加在FRF的非零元素上; PT表示总功率预算, 它是雷达系统在发射时可用的最大功率限制。需要注意的是, 在实际雷达系统中, 发射功率需要进行限制, 以确保系统以最大可用功率发射, 从而实现最佳性能表现。接下来将讨论2种功率约束: 一是对总发射功率的约束; 二是单天线约束(将在后续详细介绍)。这些约束对于雷达系统的设计和性能优化至关重要。

2 优化算法

2.1 通信全数字波束赋形矩阵求解

在通信系统中, 信道矩阵H描述了信号在发送端和接收端之间传输过程中所经过的信道效应。为了有效得到通信全数字波束赋形矩阵, 可以对信道矩阵H进行奇异值分解(singular value decomposition, SVD)来获取通信全数字波束赋形矩阵Fcom[16]。通过奇异值分解, 可以将信道矩阵H分解为3个矩阵的乘积: H=UΣVH。其中, 矩阵U为Nr×rank(H)酉矩阵; Σ为奇异值按降序排列的rank(H)×rank(H)对角矩阵; V为Nt×rank(H)酉矩阵。利用这些信息, 可以设计出最优的通信全数字波束赋形矩阵Fcom, 以最大程度地增强信号的接收效果。对于Σ和V, 可以参考文献[17]中的处理方式进行分解:

式中: Σ1为Ns×Ns维矩阵; V1为Nt×Ns维矩阵。通过提取V1矩阵, 可以得到通信全数字波束赋形矩阵Fcom, 即Fcom=V1。这种简洁的表示形式能够通过SVD分解信道矩阵右奇异向量的一部分, 实现快速计算适应信道特性的波束赋形矩阵, 从而提升通信系统性能。

2.2 雷达全数字波束赋形矩阵求解

在获取假设雷达全数字波束赋形矩阵时, 考虑采用一种简单的方法获取假设雷达全数字波束赋形矩阵: 将雷达波束的设计问题等效为对雷达的协方差矩阵进行设计。假设去蜂窝MIMO-ISAC系统中存在K个目标位于角度{φ1, φ2, …, φK}上, 因此可以将MIMO雷达波束形成器采用文献[18]给出

式中, 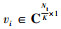由at(φi)中位于对应位置角度的元素给出。通过采用该方法, 可以有效地设计适用于去蜂窝MIMO-ISAC系统的雷达全数字波束赋形矩阵, 同时能够在仿真计算中保持较低的复杂度, 从而对雷达性能进行优化, 使其在目标探测和跟踪方面表现更准确。

2.3 辅助矩阵构造

对于辅助矩阵Faux的构造, 可以将Faux视为一个酉矩阵。因为酉矩阵具有保持向量长度和角度不变的性质, 所以它不会改变雷达波束方向。同时, 可以将这个矩阵构造问题表述为一个优化问题, 目标是最小化矩阵FradFaux与矩阵Fcom之间的欧氏距离。欧氏距离可以度量2个矩阵之间的差异程度, 即它们在空间的接近程度。通过最小化欧式距离, 容易寻找到一个最优的酉矩阵Faux, 从而提高联合通感系统的性能权衡

针对该问题, 可以同样采用奇异值分解的方法进行求解

式中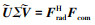：是对矩阵FradHFcom的奇异值分解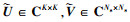，为酉矩阵; IK×Ns是由一个K×K的单位矩阵和一个K×(Ns-K)的零矩阵组成的一个K×Ns的矩形矩阵。

2.4 总功率约束性能权衡设计

在优化问题(10)中引入了一个等式约束, 这是因为在实际雷达应用中, 往往需要以其最大可用功率进行发射。这样的问题涉及到权衡设计, 实际上是一种Pareto优化[19]。通过解决加权问题(10)可以得到一组解, 这些解构成了Pareto最优集。值得注意的是, 目标函数中涉及的2个Frobenius范数可以在形式上进行组合。通过对这些范数的组合, 能够更加合理地表达优化问题

简化表示: 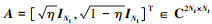, , 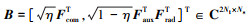问题(10)可以写成如下形式

这是一个非凸的二次约束二次规划, 可以很容易地通过半定松弛技术(semidefinite relaxation, SDR)转化为半定规划。由于存在恒模约束和二次约束, 使用SDR求解器在一般情况下计算效率不高。因此, 在本小节中提出一种基于传统正交匹配追踪算法(orthogonal matching pursuit, OMP)的改进算法去实现全局最优[17], 并且一定程度上降低复杂度。

在改进OMP算法中, 本文与传统OMP算法主要在候选矩阵的选择以及模拟波束赋形矩阵FRF的获取方式两方面存在差异。在传统OMP算法中, 候选矩阵通常是阵列响应矢量矩阵At, 本文选取了一种新的候选矩阵选择策略, 即将字典矩阵D=ηAt+(1-η)At*作为候选矩阵[20], 其中At=[at(θ1, ), …, at(θL)]为阵列响应矢量矩阵; 在获取FRF时, 本文将对误差矩阵Fres进行奇异值分解, 从而得到RF矢量。通过这种新的候选矩阵选择策略和SVD的引入, 与传统OMP算法相比可以进一步提高算法性能, 并在信号处理波束赋形问题时寻求更优解决方案。

由于目标矩阵FRF存在恒模约束, 需要对候选矩阵D进行适当的处理和调整

为简化OMP算法并提高其效率, 可以对问题(16)进行重新表述

式中, G=AFRF; DG=ADCMG为候选矩阵。改进OMP算法的详细步骤如算法1所示。

算法1    改进OMP算法

输入: A, B, PT, NtRF, 0≤ρ≤1

输出: FRF, FBB

1) 初始化FRF=0, Fres=Fopt=B

2) for i≤NtRF do

3) Ψ=DGHFres

4)

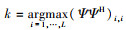
5)

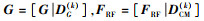
6) FBB=(GHG)-1GHB

7)

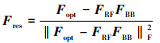
8) Fres=UΣV

9) end for

10)

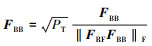
2.5 单天线功率约束性能权衡设计

与(16)式类似, 单天线功率约束的权衡问题可表示为

式中, diag(·)表示矩阵对角线元素组成的向量; 1Nt=[1, 1, …, 1]T∈RNt×1表示为全1向量。与(10)式中的等式约束不同, (19)式中的等式约束是出于确保不同天线发射的波形具有相同平均功率的目的。由于对角约束可以分离为Nt个二次等式约束, 这又导致了非凸可行域。幸运的是, 本文发现可以通过在复斜流形上建立优化问题并运用黎曼共轭梯度算法(Riemannian conjugate gradient, RCG)[21], 有效地解决问题(19)中涉及的对角等式约束。

首先, 注意到(19)式中的可行域被记为M, 形成了复斜流形。因此, 可以将问题(19)转化为以下复斜流形上的最小二乘问题

注意到, 在算法1中已经有效地表现了FRF的恒模约束, 因此可以合理地将FRFFBB视为一个整体矩阵F, 从而仅考虑对角等式约束diag(F)=1Nt·(PT/Nt), 进而在简化后续算法复杂度的同时确保其有效性。针对数字波束赋形矩阵FBB, 可以采用对FRF进行伪逆运算来求取。给定一个点F∈M处的切向量为通过F与M上任意光滑曲线相切的向量, 这些向量构成切空间Γ, 它是一个欧氏空间。斜流形的切空间可以表示为

式中, (·)ii表示矩阵的第i个对角元素。然后, 将目标函数表示为f(F)=‖AF-B‖F2。在RCG框架中, 引入了欧几里得梯度, 与传统的基于梯度的算法不同, RCG方法采用黎曼梯度来计算下降方向, 其定义为对应于切空间Γ上的正交投影的矩阵

式中, ∇f(F)=2AH(AF-B)表示为欧式梯度。接下来, RCG算法中定义了一种R映射关系, 它将切空间Γ上的点映射到M上。

式中, Z∈Γ。最后, 使用迹算子作为切空间上的内积, 即

黎曼共轭梯度算法步骤如算法2所示。

算法2    黎曼共轭梯度算法

输入: FRF, A, B, PT, 0≤ρ≤1, Δ>0

输出: FBB

1) 初始随机化F0∈M

2) J0=-gard f(F0), i=0

3) while i < imax and || grad f(Fi)||F≥Δ do

4) 梯度差异

Ji=grad f(F(i))-PF(i)(grad f(F(i-1)))

5) 组合系数

6) 下降方向

Πi=-grad f(Fi)+τipF(i)(grad f(F(i-1)))

7) 更新矩阵F(i+1)=RF(i)(μiΠi)

8) i=i+1

9) end while

10) FBB=FRF†F

3 仿真实验

本节将通过数值模拟验证所提出的波形设计方法的有效性。为确保公平性, 对所有波形设计方案施加相同的总功率预算PT=Ns, 定义信噪比为RSN=ρ/σn2, 在权重因子η=0.3条件下分别对比总功率约束和单天线功率约束下的性能表现。在仿真中考虑了以下参数: 发射AP天线数Nt=64, 接收AP天线数Nr=16。发射AP以及接收AP的相邻天线之间均采用半波长间隔的ULA天线布局, 并设定发射AP和接收AP之间存在4条收发链路, 每条链路可发送1或2个数据流。同时, 考虑到毫米波信道的多径传播情况, 设置多径数L=4。为进一步评估性能, 引入了雷达检测目标数K=3, 并对方向图设计进行了考虑, 其中发射角分别为[-π/3, 0, π/3], 信道中其余的发射角和到达角均服从[-π/2, π/2]范围内均匀分布。在模拟过程中, 设置重复实验5 000次, 每次采用不同的随机信道实现, 以获得稳健的平均结果。通过这些数值结果, 将验证所提出的波形设计方法在多种情况下的性能表现。在模拟去蜂窝MIMO-ISAC场景中, 包括2个AP、5个通信用户UE以及3个探测目标。为了实现高效的通信资源利用, 本文引入了算法频谱效率的概念, 该效率在总功率预算的限制下评估通信系统的性能。图 2展示了在总功率受限情况下的算法频谱效率, 其中对比了数据流Ns为1和2的情况, 分别计算其通信频谱效率。

通过仿真实验, 可以观察到在不同的数据流数情况下, 改进的OMP算法在接近通信全数字波形频谱效率方面表现良好。特别地, 即使在数据流数较少的情况下, 改进的OMP算法仍能有效地逼近最优效率。这证明了一体化系统在混合波束总功率预算下实现了通信感知一体化的能效。

进一步, 图 3展示了在与图 2相同设定下, 考虑单天线功率约束情况下的频谱效率。相比总功率预算, 采用单天线功率约束的混合波束方案表现更佳, 且与全数字波形频谱效率相比有明显改进, 尽管在总功率约束下也有轻微提升。接下来, 为了比较权重因子对通信性能的影响, 在单天线功率约束的混合波束方案中, 对比了几种不同因子下的通信谱效率, 其结果见图 4。

通过观察, 可以发现在权重因子越接近于1时, 通信性能越好。为了更好地体现改进OMP算法在总功率约束条件下的通感性能, 在图 5中实验设置约束条件为总功率约束, 权重因子为0.3的情况下, 对比了原OMP算法与改进OMP的性能。根据结果显示, 可判断出所提算法较之原OMP在通信和感知性能中均有提升。

从表 1可以看出改进OMP算法较原OMP算法提高了算法复杂度, 但对于提升的通感性能而言, 是可以被容忍的。

根据图 4中对权重因子的不同考虑, 随后对感知性能也做了相应对比。在图 7~9中, 实验对比了在总功率约束和单天线功率约束下的雷达波形图与雷达全数字波束图的差异, 并对3种波束设置不同权重因子进行性能评估。实验表明, 在权重因子为0.3时, 可以得到近乎于雷达全数字波束图一致的轨迹。同时在3种不同因子中, 单天线约束下的感知性能也比总功率约束下的感知性能要好。

thumbnail 图1

仿真布局
thumbnail 图2

总功率约束下的性能表现
thumbnail 图3

单天线功率约束下的性能表现
thumbnail 图4

不同功率约束下的雷达方向图
thumbnail 图5

通信性能对比
thumbnail 图6

感知性能对比
表1

算法复杂度对比

thumbnail 图7

权重因子为0.3时的雷达波束方向图
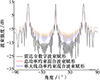thumbnail 图8

权重因子为0.5时的雷达波束方向图
thumbnail 图9

权重因子为0.7时的雷达波束方向图

4 结论

本研究探讨在去蜂窝MIMO-ISAC场景下, 通信资源利用和算法频谱效率对系统性能的影响。通过改进的OMP算法在不同数据流和功率约束下的仿真, 评估了系统的能效和频谱利用。实验表明, 在单天线功率约束下, 混合波束方案表现更佳, 较全数字波形频谱效率有显著提升, 证实了其在此系统中的优势。同时, 又比较了这2种约束下的雷达波形图与全数字波束图的性能, 2种波束均能接近理想雷达波束, 满足感知任务需求, 单天线功率约束表现稍优。

References

  1. LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and vommunications: toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. [Article] [CrossRef] [Google Scholar]
  2. LIU Xiang, HUANG Tangyao, SHLEZINGER N, et al. Joint transmit beamforming for multiuser mimo communications and MIMO radar[J]. IEEE Trans on Signal Processing, 2020, 68: 3929–3944. [Article] [NASA ADS] [CrossRef] [Google Scholar]
  3. CHENG Haowen, LI Xiang, ZHUANG Zhaowen. A rising radar system——MIMO radar[J]. Acta Electronica Sinica, 2012, 40(6): 1190–1198. [Article] (in Chinese) [Google Scholar]
  4. XU Youyun, XU Kui. Cel-free ultra-massive MIMO and high-frequency band wireless access technology for integrated sensing and communication[J]. Mobile Communications, 2022, 46(5): 17–25 (in Chinese) [Google Scholar]
  5. GHOSH A, RATASUK R, MONDAL B, et al. LTE-advanced: next-generation wireless broadband technology[J]. IEEE Wireless Communications, 2010, 17(3): 10–22. [Article] [Google Scholar]
  6. DAVID L P, ISMAIL G, GUILLAUME R, et al. Enhanced intercell interference coordination challenges in heterogeneous networks[J]. IEEE Wireless Communications, 2011, 18(3): 22–30. [Article] [Google Scholar]
  7. NAQVI S H R, HO P H. Achieving 5G NR mmWave indoor coverage under integrated access backhaul[J]. IEEE Systems Journal, 2021, 15(4): 5429–5439. [Article] [CrossRef] [Google Scholar]
  8. RAI P K, HENNING I, YAKKATI R, et al. Localization and activity classification of unmanned aerial vehicle using mmWave FMCW radars[J]. IEEE Sensors Journal, 2021, 21(14): 16043–16053. [Article] [CrossRef] [Google Scholar]
  9. WILCOX D, SELLATHURAI M. On MIMO radar subarrayed transmit beamforming[J]. IEEE Trans on Signal Processing, 2011, 60(4): 2076–2081 [Google Scholar]
  10. XU Hao, ZHOU Pengguang, ZHANG Shuchang. Hybrid beamforming algorithm in millimeter-wave MIMO system[J]. Study on Optical Communications, 2017(5): 75–78 (in Chinese) [Google Scholar]
  11. GOLDSMITH A, JAFAR S A, JINDAL N, et al. Capacity limits of MIMO channels[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(5): 684–702. [Article] [CrossRef] [Google Scholar]
  12. ZHANG Didi, WANG Yafeng, LI Xuehua, et al. Hybridly connected structure for hybrid beamforming in mmwave massive MIMO systems[J]. IEEE Trans on Communications, 2017, 66(2): 662–674 [Google Scholar]
  13. GONZÁLEZ-PRELCIC N, MÉNOEZ-RIAL R, HEATH R W. Radar aided beam alignment in mmWave V2I communications supporting antenna diversity[C]//2016 Information Theory and Applications Workshop, 2016: 1–7 [Google Scholar]
  14. LI Jian, STOICA P, XIE Yao. On probing signal design for MIMO radar[C]//2006 Fortieth Asilomar Conference on Signals, Systems and Computers, 2006: 31–35 [Google Scholar]
  15. CHENG Ziyang, LIAO Bin, HE Zishu, et al. Joint design of the transmit and receive beamforming in MIMO radar systems[J]. IEEE Trans on Vehicular Technology, 2019, 68(8): 7919–7930. [Article] [CrossRef] [Google Scholar]
  16. VIKLANDS T. Algorithms for the weighted orthogonal procrustes problem and other least squares problems [D]. Uppsala, Sweden: Uppsala University, 2006 [Google Scholar]
  17. EL A O, RAJAGOPAL S, ABU-SURRA S, et al. Spatially sparse precoding in millimeter wave MIMO systems[J]. IEEE Trans on Wireless Communications, 2014, 13(3): 1499–1513. [Article] [CrossRef] [Google Scholar]
  18. HASSANIENA, VOROBYOV S A. Phased-MIMO radar: a tradeoff between phased-array and MIMO radars[J]. IEEE Trans on Signal Processing, 2010, 58(6): 3137–3151. [Article] [NASA ADS] [CrossRef] [Google Scholar]
  19. BOYD S, VANDERBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004 [CrossRef] [Google Scholar]
  20. LI Xiaohui, LI Huanyang, LYU Siting, et al. Hybrid beamforming algorithm in mmWave integrated sensing and communication[J]. Systems Engineering and Electronics, 2023, 45(5): 1512–1517 (in Chinese) [Google Scholar]
  21. LIU Fang, MASOUROS C, LI Ang, et al. MU-MIMO communications with MIMO radar: from co-existence to joint transmission[J]. IEEE Trans on Wireless Communications, 2018, 17(4): 2755–2770. [Article] [NASA ADS] [CrossRef] [Google Scholar]

All Tables

表1

算法复杂度对比

In the text

All Figures

thumbnail 图1

仿真布局
In the text
thumbnail 图2

总功率约束下的性能表现
In the text
thumbnail 图3

单天线功率约束下的性能表现
In the text
thumbnail 图4

不同功率约束下的雷达方向图
In the text
thumbnail 图5

通信性能对比
In the text
thumbnail 图6

感知性能对比
In the text
thumbnail 图7

权重因子为0.3时的雷达波束方向图
In the text
thumbnail 图8

权重因子为0.5时的雷达波束方向图
In the text
thumbnail 图9

权重因子为0.7时的雷达波束方向图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.