A WLAN-oriented distributed hierarchical parallel simulation method

Wenfei JIA; Mao YANG; Zhongjiang YAN; Bo LI

doi:10.1051/jnwpu/20244250895

All issues

Volume 42 / No 5 (October 2024)

JNWPU, 42 5 (2024) 895-902

Full HTML

Open Access

Issue		JNWPU Volume 42, Number 5, October 2024


Page(s)		895 - 902
DOI		https://doi.org/10.1051/jnwpu/20244250895
Published online		06 December 2024

JNWPU 2024, 42(5): 895–902

A WLAN-oriented distributed hierarchical parallel simulation method

一种面向WLAN的分布式分层并行仿真方法

Wenfei JIA (贾雯斐), Mao YANG (杨懋), Zhongjiang YAN (闫中江) and Bo LI (李波)

School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China

Received: 25 July 2023

Abstract

To solve the problem that the efficiency decreases with the increase of terminal nodes in wireless local area network(WLAN) distributed parallel simulation, a WLAN-oriented distributed hierarchical parallel simulation method is proposed. Firstly, considering the WLAN star network topology, the process of the simulated access point (AP) is denoted as the main process, which is responsible for time synchronization with the other processes of the simulated station (STA) nodes in the WLAN network. Secondly, the processes of all simulated STAs are then evenly divided into groups, and the group leader is responsible for the synchronization of processes within the group. Then, after the main process broadcasts the simulation start event, the group leader process firstly collects the end message of the group member's terminal node, and then reports to the main process. A three-layer hierarchical structure is constructed, consisting of the main process layer, the group leader process layer and the group member process layer. Finally, the time gain factor of the hierarchical simulation method is analyzed and obtained in closed-form expression, under the different computational loads. Simulation results show that comparing to the existing non-hierarchical simulation method, when the average computational load is 1.2x time unit and the nodes number is 100, the gain of the proposed method can reach 50%.

摘要

针对采用分布式并行方法仿真WLAN(wireless local area network)场景时存在的随终端节点个数增加而效率降低的问题, 提出了一种面向WLAN的分布式分层并行仿真方法。基于WLAN的星状网络拓扑结构, 令仿真接入节点的进程为主进程, 负责WLAN全网中其他仿真节点的时间同步; 将所有仿真终端节点的进程均匀分为若干组, 由组长负责该组内进程的同步。在主进程广播仿真开始事件后, 组长进程先收集本组组员终端节点推进结束消息, 当收齐后再向主进程汇报。形成"主进程-组长进程-组员进程"的3层分层结构。在不同计算负荷下, 仿真分析并得到了分层仿真方法的时间增益因子闭合表达式。仿真结果表明, 与现有不分层的仿真方法相比, 当平均计算负荷为1.2倍单位时长、节点个数为100时, 所提分层仿真方法的增益可达50%。

Key words: WLAN / hierarchical algorithm / parallel simulation

关键字 : WLAN / 分层算法 / 并行仿真

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

无线局域网(wireless local area network, WLAN)因为其部署成本低和可扩展性好等优点, 得到了迅猛发展。有报告[1]指出: 2021年全球企业WLAN收入到达76亿美元, 同比增长20.4%。电气和电子工程师协会(institute of electrical engineers, IEEE)制定的第一代WLAN标准IEEE802.11[2]成为WLAN发展的重要里程碑。为了应对更大数据量、更密集场景部署和更低时延要求带来的挑战, 下一代WLAN的标准[3]计划于2024年发布。

无线通信仿真系统相较于搭建硬件仿真环境具有成本低、可拓展性高和易于调整等特点。利用仿真软件可以较快地搭建仿真场景以验证和改进协议, 极大地提高了协议开发的效率。这使得软件仿真成为了标准化推动过程中, 开发和验证网络协议的重要工具。NS-3是一款用于WLAN的主流仿真软件, 始于2006年[4], 目前已经迭代发展到3.39版本[5]。其对外提供的大量扩展接口让用户可以方便地开发需要的模块或者构建自己的通信场景。由于其基于社区开源的特点以及网络计算的快速发展, NS-3的维护和开发从未停止[6]。文献[7]通过NS-3仿真软件搭建了DSC(dynamic sensitivity control)仿真平台和上行OFDMA(orthogonal frequency division multiple access)仿真平台, 分别验证了所提DSC算法和上行OFDMA算法的性能。文献[8]通过NS-2仿真软件搭建的仿真平台, 验证了MU MAC(multi-user media access control)协议相较于802.11ac协议的性能增益。

随着通信网络的快速发展, 网络协议和仿真系统模型变得复杂[9]。在仿真高密集网络或重负载行为时, 仿真时长增长迅速, 使仿真的效率降低, 阻碍协议算法的开发和验证[10]。并行仿真旨在用并行的计算方式提高仿真的效率[11]。文献[12]提出了基于多核CPU的仿真计算并行加速方法和基于集群的高效CPU并行计算方法, 有效提高了通信仿真效率。文献[13]提出2级混合并行结构, 对原有的仿真程序进行改写, 测试结果证明了分布式并行计算的可行性和有效性。文献[14]将划分好的子任务分配给不同节点进行仿真, 通过进程间通信保证各节点间的同步, 测试结果表明分布式并行仿真的有效性。

NS-3也面临着需要加速仿真的问题。文献[10]通过减少NS-3仿真平台中不必要的仿真事件, 提高仿真速度。为了支持分布式并行仿真, NS-3使用标准的消息传递接口(message passing interface, MPI)处理多个进程之间发送和接收消息的过程。文献[15]从优化同时刻的异常事件任务、改进网络划分算法和流量分摊方法三方面改进并行方法以提高仿真效率。然而，NS-3等仿真平台采用分布式并行方法仿真WLAN场景依然存在问题。接入点(access point, AP)是指无线局域网用户终端接入网络的设备。终端(station, STA)是指每一个连接到无线网络中的用户设备。空消息(null message)是指子进程完成当前周期的仿真任务后, 向目标进程发送的等待同步标记信息。在利用空消息同步策略确保AP和STA之间的仿真同步时, 存在随STA个数增长而效率降低的问题。

针对上述问题, 本文提出了一种面向WLAN的分布式分层并行仿真方法, 仿真结果表明所提方法可以有效降低AP收集所有STA的空消息需要消耗的时间随STA个数增大而增加的幅度, 进而解决仿真效率降低的问题。

1 系统建模

1.1 WLAN系统模型

WLAN的基本元素为接入点和终端。本文讨论的背景是基于AP组建的基础无线网络。其拓扑形式为常见的星状网络拓扑, 如图 1所示。

AP负责接收和转发其他STA发出的信息; STA只需要将试图发送的信息发送给AP, 并接收从AP转发而来的信息。也就是说网络中所有的通信都是由AP来转发完成。

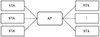图1

WLAN中的星状拓扑

1.2 仿真系统模型

无论是星状拓扑还是非星状拓扑, 利用分布式并行仿真方法加速WLAN协议的仿真时, 为了充分利用多核的并行性能, 每个处理器核心上只部署一个节点(AP或STA)的仿真进程。仿真AP的进程与仿真STA的进程通过MPI建立点对点连接以传递空消息，从而同步进程。为方便后续讨论, 将仿真AP的进程命名为主进程, 将仿真STA的进程命名为子进程。假设有n个子进程和1个主进程, 形成的网络拓扑如图 2所示。

分布式并行仿真需要确保不同进程间的时间同步。因为空消息同步策略具有良好的拓展性, 所以选择此策略进行主、子进程之间的仿真同步。工作流程如图 3所示: 主进程先广播仿真开始事件, 然后接收子进程发来的空消息(也称推进结束消息), 当收齐后开始广播下一轮仿真开始事件; 子进程收到仿真开始事件后处理事件队列中的仿真任务, 当处理完后通过MPI向主进程发送空消息, 接着阻塞接收下一轮仿真开始事件。

为方便后续分析与讨论, 做如下定义。在给出定义的基础上, 做部分假设。

定义1 计算负荷: 表示子进程在一个同步周期内完成仿真任务需要消耗的墙上时间(wall-clock time)。计算负荷为一随机变量, 用参数μ表示均值。

定义2 t_null: 表示每个子进程发送的空消息被目标进程接收处理的时间。

假设1 每个子进程的计算负荷是独立同分布的随机变量。

假设2 t_null的大小是固定的[5]。

假设3 主进程同时能接收处理一个空消息。

用T_nh表示采用传统空消息同步策略时, 主进程收齐所有子进程的空消息所需的时间。按照图 3所示的基于传统空消息同步策略的分布式并行仿真方法, T_nh的取值满足不等式(1)。

即T_nh的最小值等于n个子进程发送空消息到主进程被接收处理所需时间的线性叠加。这会导致当STA个数较大时, AP收集所有STA的空消息消耗的时间占整个仿真时间的比重变大, 导致仿真效率降低。

该问题由t_null的线性叠加导致, 可以通过引入分层思想消除AP收集所有STA的空消息消耗的时间与n个t_null之间的线性关系, 提高仿真效率。

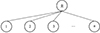图2

仿真系统网络拓扑

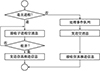图3

传统空消息同步策略

2 分布式分层并行仿真方法

2.1 核心思想与工作流程

分布式分层并行仿真方法包含分层流程和基于分层结果的仿真方法。对仿真系统中的n个子进程进行分组, 每组有m个子进程, 共分为n/m组。每个组包含1个组长进程和m-1个组员进程。分组之后的子进程和1个主进程形成如图 4所示的拓扑。

基于分层结果的仿真方法工作流程如图 5所示: 主进程先广播仿真开始事件, 然后接收组长进程发来的空消息, 当收齐后开始广播下一轮仿真开始事件; 组员进程收到仿真开始事件后处理事件队列中的仿真任务, 当处理完后通过MPI向组长进程发送空消息, 接着阻塞接收下一轮仿真开始事件; 组长进程收到仿真开始事件后处理事件队列中的仿真任务, 当处理完后开始接收组员进程发来的空消息, 当收齐后通过MPI向主进程发送空消息, 接着阻塞接收下一轮仿真开始事件。用T_h表示采用分布式分层并行仿真方法时, 主进程收齐所有子进程的空消息所需的时间。

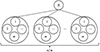图4

分层下的仿真系统网络拓扑

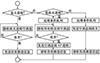图5

分布式分层并行仿真方法

2.2 增益因子

将分布式分层并行仿真方法应用于分布式并行仿真是为了消除AP收集所有STA的空消息消耗的时间与n个t_null之间的线性关系, 即减少主进程收齐所有子进程的空消息所需的时间随子进程个数增大而增加的幅度, 进而提高仿真效率。定义(2)式所示变量为增益因子以衡量所提分布式分层并行仿真方法的性能增益。

将在第3节理论建模并分析G的值。

3 理论分析

平均计算负荷μ=0时，对G的分析结论可由平均计算负荷μ≠0的分析结论退化得到, 因此本节首先分析当μ≠0时的增益。考虑主进程在一次仿真同步过程中用于收集所有子进程的空消息所需的时间, 为方便讨论与分析, 做出如下假设:

假设4 n个子进程收到仿真开始事件的时间是相同的, 不妨将其固定为0。

假设5 组长进程必须完成当前同步周期内的仿真任务后才能接收组员进程的空消息。

3.1 平均计算负荷非零时(μ≠0)的增益G分析

首先推导计算不采用和采用分层算法下的仿真耗时T_nh和T_h的表达式, 然后求解得到增益因子G的表达式, 最后对增益因子做出分析。

3.1.1 不采用分层算法

设n个子进程和1个主进程采用基于传统空消息同步策略的分布式并行仿真方法, 此时T_nh的计算过程如下。令T_i(i=1, 2, …, n, n∈N⁺)表示子进程i的计算负荷。T_(i)表示第i个空消息到达主进程的时间。主进程处理第i个空消息之前, 必须等待前i-1个空消息都被处理完毕。因此, 主进程处理完第i个空消息所需的时间X_i如(3)式所示。

主进程处理完第n个空消息所需的时间X_n可以通过(4)式所示的递推公式组得到。

利用递推公式组可化简X_n的表达式为

式中, T_(i)为T_i的顺序统计量。T_i是独立同分布的随机变量, 其分布函数为F_{T_i}(x), 密度函数为f_{T_i}(x)。根据顺序统计量的性质, T_(i)的分布函数和密度函数如(6)式所示。

综上, T_nh的取值如(7)式所示。

3.1.2 采用分层算法

设n个子进程和1个主进程采用分布式分层并行仿真方法, 此时T_h的计算过程如下: 令T_{i, 0}(i=1, 2, …, n/m)表示组长进程i的计算负荷, T_{i, j}(i=1, 2, …, n/m, j=1, 2, …, m-1)表示第i组的组员进程j的计算负荷。T_{(i, j)}表示第j个空消息到达组长进程i的时间。组长进程必须在完成当前同步周期内的仿真任务后才能接收组员进程的空消息, 所以组长进程i处理完第1个空消息所需的时间X_{1, i}如(8)式所示。

组长进程处理第j个空消息之前, 必须等待前j-1个空消息都被处理完毕。因此, 组长进程i处理完第j个空消息所需的时间X_{j, i}如(9)式所示。

组长进程i处理完第m-1个空消息所需的时间X_{m-1, i}可以通过(10)式所示的递推公式组得到。

可利用递推公式组化简X_{m-1, i}的表达式为

式中, T_{i, 0}是均值为μ的随机变量。T_{(i, j)}为T_{i, j}(i=1, 2, …, n/m, j=1, 2, …, m-1)的顺序统计量。T_{i, j}是独立同分布的随机变量, 其分布函数为F_{T_{i, j}}(x), 密度函数为f_{T_{i, j}}(x)。根据顺序统计量的性质, T_{(i, j)}的分布函数和密度函数如(12)式所示。

X_{(m-1, i)}表示第i个来自组长子进程的空消息到达主进程的时间。主进程在处理第i个空消息之前, 必须等待前i-1个空消息都被处理完毕。因此, 主进程处理完第i个空消息所需的时间Y_i如(13)式所示。

主进程处理完第n/m个空消息所需的时间Y_n/m可以通过(14)式所示的递推公式组得到。

利用递推公式组化简Y_n/m的表达式为

综上, T_h的取值如(16)式所示。

式中, X_{(m-1, i)}为X_{m-1, i}的顺序统计量。

3.1.3 增益因子

平均计算负荷非零时(μ≠0)的增益因子表达式如(17)式所示。

从(17)式可以得到如下结论: 增益不仅与STA总个数及每组内STA个数有关, 还与t_null的大小和计算负荷的大小有关。在每个子进程发送的空消息被目标进程接收处理的时间t_null一定时, 计算负荷越大, 每个STA完成一个同步周期中的仿真任务需要消耗的墙上时间就越长, T_h和T_nh间的差距越无法由t_null所体现。由于此时分层算法带来的并行性效果有所下降, 增益相应地也会下降。

3.1.4 计算负荷服从指数分布

由于通信系统中各个节点的包到达间隔一般服从指数分布, 因此, 仿真每个节点的子进程的计算负荷可假设为独立同分布的随机变量且服从参数为λ的指数分布, 此时μ=1/λ。

此时增益因子G的表达式可以进一步退化。(17)式中的X_{(m-1, i)}是X_{m-1, i}的顺序统计量。X_{m-1, i}的表达式由(11)式给出。T_{(i, j)}的分布函数和密度函数由(18)式给出。

T_{i, 0}的分布函数和密度函数由(19)式给出。

T_(i)的分布函数和密度函数由(20)式给出。

3.2 平均计算负荷为零时(μ=0)的增益G分析

在推导出μ≠0的结论后, 对相关公式做部分退化处理即可得到μ=0的相关结论。先分析μ=0情形下T_nh和T_h的表达式, 然后求解得到增益因子G的表达式, 最后对增益因子做出分析。

3.2.1 不采用分层算法

因为μ=0, 所以(7)式中的T_(i)满足T_(i)≡0。此时(7)式可退化为(21)式。

3.2.2 采用分层算法

因为μ=0, 所以(11)式可退化为(22)式。(16)式可退化为(23)式。

3.2.3 增益因子

平均计算负荷为零时(μ=0)的增益因子如(24)式所示。此时增益只与STA总个数以及每组内STA个数有关。

4 仿真分析

针对μ=0的情形, 本节仿真了增益随STA总个数以及每组内STA个数增加时的变化情况。针对μ≠0的情形, 本节进行计算负荷服从指数分布情况下的仿真分析，包括增益随STA总个数、每组内STA个数、μ值大小和t_null值大小改变的变化情况。本文选择的对比算法为NS-3采用的基于传统空消息同步策略的分布式并行仿真方法[5], 后续增益结果均为所提分布式分层仿真方法相较于对比算法能够取得的增益。

4.1 平均计算负荷为零时(μ=0)的算法性能

仿真节点个数取值在40~480范围内，以40为步进值变化, 组内节点个数取值为10, 20或40时的增益情况。

图 6中横坐标代表了节点个数, 纵坐标代表了所提方案相较于采用空消息同步策略的传统分布式并行仿真的增益, 数值越大, 所提方案降低AP收集所有STA的空消息需要消耗的时间随STA个数增大而增加的幅度越大。从图 6可知, 组内子进程个数一定, 随着节点个数的增加, 增益不断提高。节点数达到480时, 增益可以达到90%左右。节点个数不变, 组内子进程个数增加, 增益并不是一直降低。

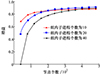图6

不同组内成员个数下, 增益变化情况

4.2 平均计算负荷非零时(μ≠0)的算法性能

仿真节点个数取值在40~100范围内，以20为步进值变化, 组内节点个数取值为20, 计算负荷的均值μ取值为1倍单位时间, t_null取值在0.12~0.16倍单位时间范围内，以0.02倍单位时间为步进值变化时主进程收齐所有子进程空消息所需的时间和增益情况。

图 7中横坐标是节点个数, 纵坐标是主进程收齐所有子进程的空消息所需的时间。从图 7可知, t_null不变, 节点个数较大时, 采用分层的耗时相较于非分层有明显减少, 且减少量随着节点个数增加而增加。相同节点个数时, t_null越大, 采用分层的耗时相较于非分层的减少量越大。

图 8中横坐标代表了节点个数, 纵坐标代表了所提方案相较于采用空消息同步策略的传统分布式并行仿真的增益。从图 8可知, 节点个数不变, 随着t_null的增大, 增益变大。因为分层带来的并行效果主要是减少t_null的线性叠加。t_null不变, 随着节点个数的增加, 增益不断提高。原因是节点个数越多, 分层带来的并行性更高。节点个数为100, t_null=0.16, 可以取得60%以上的增益; t_null=0.12, 可以取得50%以上的增益。

仿真节点个数取值在40~100范围内，以20为步进值变化, 组内节点个数取值为20, 计算负荷均值μ取值在1~1.2倍单位时间范围内，以0.1倍单位时间为步进值变化, t_null取值为0.14倍单位时间时的主进程收齐所有子进程的空消息所需的时间和增益情况。

图 9中横坐标是节点个数, 纵坐标是主进程收齐所有子进程的空消息所需时间。从图 9可知, 计算负荷均值不变, 节点个数较大时, 采用分层的耗时相较于非分层有明显减少, 且减少量随着节点个数增加而增加。计算负荷均值变化对分层的耗时影响较大, 对非分层的耗时影响较小。相同节点个数时, 计算负荷均值越大, 采用分层的耗时相较于非分层的减少量越小。

图 10中横坐标代表了节点个数, 纵坐标代表了所提方案相较于采用空消息同步策略的传统分布式并行仿真的增益。从图 10可知, 节点个数不变, 随着计算负荷均值增大, 增益降低。因为计算负荷的增加降低了分层带来的并行效果。节点个数为100, 计算负荷均值为1, 可以取得近60%的性能增益。

仿真节点个数取值在40~160范围内，以40为步进值变化, 组内节点个数取值为10, 20或40, 计算负荷的均值μ取值为1倍单位时间, t_null取值为0.14倍单位时间时的主进程收齐所有子进程的空消息所需的时间和增益情况。

图 11中横坐标是节点个数, 纵坐标是主进程收齐所有子进程的空消息所需的时间。非分层不涉及分组, 故非分层在图中只有一条曲线。从图中可知, 节点个数较大时, 采用分层的耗时相较于非分层有明显减少, 且减少量随着节点个数增加而增加。组内成员个数变化对分层的耗时影响较大。

图 12中横坐标代表了节点个数, 纵坐标代表了所提方案相较于采用空消息同步策略的传统分布式并行仿真的增益。从图 12可知, 增益的理论值和仿真值吻合良好。节点个数在40~160之间变化时, 随着组内子进程个数增加, 分层相较于非分层的增益降低。

不同t_null下, 耗时变化情况

不同t_null下, 增益变化情况

不同计算负荷均值下, 耗时变化情况

不同计算负荷均值下, 增益变化情况

不同组内成员个数下, 耗时变化情况

不同组内成员个数下, 增益变化情况

5 结论

诸如NS-3等仿真平台采用分布式并行方法仿真WLAN场景时, 传统的空消息同步策略会导致仿真AP节点的进程收齐仿真STA节点的进程的推进结束消息所需要的时间随STA个数增长而线性增长最终导致效率降低问题。针对该问题本文提出一种面向WLAN的分布式分层并行仿真方法, 并分析了分层相较于非分层的增益。仿真表明所提方法可有效降低仿真耗时。

References

BRANDON Butler. Worldwide enterprise WLAN market shows strong growth in Q4 and the full year 2021, according to IDC[EB/OL]. (2022-03-09)[2023-07-14]. https://www.idc.com/getdoc.jsp?containerId=prUS48940222">[Article] [Google Scholar]
CROW B P, WIDJAJA I, KIM J G, et al. IEEE 802.11 wireless local area networks[J]. IEEE Communications Magazine, 1997, 35(9): 116–126. [Article] [CrossRef] [Google Scholar]
KHOROV E, LEVITSKY I, AKYILDIZ I F. Current status and directions of IEEE 802.11be, the future Wi-Fi 7[J]. IEEE Access, 2020, 8: 88664–88688. [Article] [NASA ADS] [CrossRef] [Google Scholar]
RU Xinyu, LIU Yuan, CHEN Wei. Research review of new network simulator NS-3[J]. Micromachinesand Applications, 2017, 36(20): 14–16 (in Chinese) [Google Scholar]
NS-3 Project. NS-3 network simulator[EB/OL]. (2023-07-05)[2023-07-14]. [Article] [Google Scholar]
LIU Ruijun. Based on NS-3 of multibeam satellite communication simulation system design and implementation[D]. Xi'an : Xidian University, 2021 (in Chinese) [Google Scholar]
ZHANG Zhenya. Design and implementation of simulation platform for key technologies of next-generation WLAN[D]. Xi'an: Xidian University, 2015 (in Chinese) [Google Scholar]
ZHOU Run, LI Bo, YANG Mao, et al. Simulation research on next-generation WLAN multi-user multi-access technology[J]. Computer Simulation, 2019, 36(8): 288–292 (in Chinese) [Google Scholar]
VOICU A M, SIMIC L, PETROVA M. Modelling large-scale CSMA wireless networks[C]//2021 IEEE Wireless Communications and Networking Conference, Nanjing, 2021: 1–6 [Google Scholar]
MA Yinghua. Research on WLAN simulation event aggregation and NS-3 acceleration technology[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2022 (in Chinese) [Google Scholar]
XIN Y, YANG M, YAN Z, et al. Non-uniform time slice parallel simulation method based on offline learning for IEEE 802.11ax[C]//Lecture Notes of the Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering, 2023: 161–171 [Google Scholar]
LU Hong. Efficient parallel computing method and implementation of load in a new generation of wireless communication simulation system[D]. Beijing: Beijing University of Posts and Telecommunications, 2018 (in Chinese) [Google Scholar]
NING Yuanting. Research on improvement of computational simulation software of three-dimensional discrete element method based on MPI[D]. Jilin: Jilin University, 2015 (in Chinese) [Google Scholar]
JIANG Huanan, ZHANG Shuai, LIN Yufei, et al. Simulation optimization and testing of distributed parallel Gazebo based on MPI[J]. Computer Science, 2021, 48(suppl 2): 672–677 (in Chinese) [Google Scholar]
YUAN Jin. Research on network parallel simulation method based on NS-3[D]. Chengdu: University of Electronic Science and Technology of China, 2017 (in Chinese) [Google Scholar]

All Figures

	图1 WLAN中的星状拓扑
In the text

	图2 仿真系统网络拓扑
In the text

	图3 传统空消息同步策略
In the text

	图4 分层下的仿真系统网络拓扑
In the text

	图5 分布式分层并行仿真方法
In the text

	图6 不同组内成员个数下, 增益变化情况
In the text

	图7 不同t_null下, 耗时变化情况
In the text

	图8 不同t_null下, 增益变化情况
In the text

	图9 不同计算负荷均值下, 耗时变化情况
In the text

	图10 不同计算负荷均值下, 增益变化情况
In the text

	图11 不同组内成员个数下, 耗时变化情况
In the text

	图12 不同组内成员个数下, 增益变化情况
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] BRANDON Butler. Worldwide enterprise WLAN market shows strong growth in Q4 and the full year 2021, according to IDC[EB/OL]. (2022-03-09)[2023-07-14]. https://www.idc.com/getdoc.jsp?containerId=prUS48940222">[Article] [Google Scholar]

[2] CROW B P, WIDJAJA I, KIM J G, et al. IEEE 802.11 wireless local area networks[J]. IEEE Communications Magazine, 1997, 35(9): 116–126. [Article] [CrossRef] [Google Scholar]

[3] KHOROV E, LEVITSKY I, AKYILDIZ I F. Current status and directions of IEEE 802.11be, the future Wi-Fi 7[J]. IEEE Access, 2020, 8: 88664–88688. [Article] [NASA ADS] [CrossRef] [Google Scholar]

[4] RU Xinyu, LIU Yuan, CHEN Wei. Research review of new network simulator NS-3[J]. Micromachinesand Applications, 2017, 36(20): 14–16 (in Chinese) [Google Scholar]

[5] NS-3 Project. NS-3 network simulator[EB/OL]. (2023-07-05)[2023-07-14]. [Article] [Google Scholar]

[6] LIU Ruijun. Based on NS-3 of multibeam satellite communication simulation system design and implementation[D]. Xi'an : Xidian University, 2021 (in Chinese) [Google Scholar]

[7] ZHANG Zhenya. Design and implementation of simulation platform for key technologies of next-generation WLAN[D]. Xi'an: Xidian University, 2015 (in Chinese) [Google Scholar]

[8] ZHOU Run, LI Bo, YANG Mao, et al. Simulation research on next-generation WLAN multi-user multi-access technology[J]. Computer Simulation, 2019, 36(8): 288–292 (in Chinese) [Google Scholar]

[9] VOICU A M, SIMIC L, PETROVA M. Modelling large-scale CSMA wireless networks[C]//2021 IEEE Wireless Communications and Networking Conference, Nanjing, 2021: 1–6 [Google Scholar]

[10] MA Yinghua. Research on WLAN simulation event aggregation and NS-3 acceleration technology[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2022 (in Chinese) [Google Scholar]

[11] XIN Y, YANG M, YAN Z, et al. Non-uniform time slice parallel simulation method based on offline learning for IEEE 802.11ax[C]//Lecture Notes of the Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering, 2023: 161–171 [Google Scholar]

[12] LU Hong. Efficient parallel computing method and implementation of load in a new generation of wireless communication simulation system[D]. Beijing: Beijing University of Posts and Telecommunications, 2018 (in Chinese) [Google Scholar]

[13] NING Yuanting. Research on improvement of computational simulation software of three-dimensional discrete element method based on MPI[D]. Jilin: Jilin University, 2015 (in Chinese) [Google Scholar]

[14] JIANG Huanan, ZHANG Shuai, LIN Yufei, et al. Simulation optimization and testing of distributed parallel Gazebo based on MPI[J]. Computer Science, 2021, 48(suppl 2): 672–677 (in Chinese) [Google Scholar]

[15] YUAN Jin. Research on network parallel simulation method based on NS-3[D]. Chengdu: University of Electronic Science and Technology of China, 2017 (in Chinese) [Google Scholar]