| Issue |
JNWPU
Volume 42, Number 2, April 2024
|
|
|---|---|---|
| Page(s) | 362 - 367 | |
| DOI | https://doi.org/10.1051/jnwpu/20244220362 | |
| Published online | 30 May 2024 | |
Single snapshot DOA estimation algorithm based on high-order power in LDACS
基于高阶幂的单快拍LDACS系统波达方向估计
CAAC Key Laboratory of Civil Aviation Wide Surveillance and Safety Operation Management & Control Technology, Civil Aviation University of China, Tianjin 300300, China
Received:
21
April
2023
The L-band digital aeronautical communication system (LDACS) is one of the essential infrastructures for future aviation broadband communication. To address the problem of interference from adjacent high-power distance measuring equipment (DME) signals, a joint orthogonal projection interference suppression and single-snapshot sparse decomposition direction of arrival (DOA) estimation method is proposed. Firstly, the DME interference is suppressed by using the subspace projection, and then a pseudo-covariance matrix is constructed by using single-snapshot data. High-order power of the pseudo-covariance matrix is calculated, followed by singular value decomposition and sparse solution obtained using constraints to estimate the desired target. The proposed method in this paper reduces the impact of noise by utilizing high-order pseudo-covariance matrix, enabling accurate estimation of the DOA of OFDM signals with only a single snapshot. Simulation results show that the estimation accuracy by using ISS-HOP-L1-SVD algorithm is better than that via ISS-HOP-MUSIC algorithm. This method can effectively suppress DME interference and improve the performance of the OFDM receiver.
摘要
L波段数字航空通信系统(L band digital aeronautical communication system, LDACS)是未来航空宽带通信重要的基础设施之一, 针对LDACS信号容易受到相邻波道大功率测距仪(distance measuring equipment, DME)信号干扰的问题, 提出了联合正交投影干扰抑制与单快拍稀疏分解的波达方向(direction of arrival, DOA)估计方法。通过子空间投影抑制DME干扰, 然后使用单快拍数据构建伪协方差矩阵, 对伪协方差矩阵求高阶幂, 之后进行奇异值分解, 并利用约束条件求解稀疏解得到期望信号来向的估计值。所提方法使用高阶伪协方差矩阵降低了噪声影响, 仅用单快拍就可以准确估计LDACS信号的入射方向。仿真结果表明, 改进单快拍高级幂(improved single snapshot high order power, ISS-HOP)L1-SVD算法的估计精度优于ISS-HOP-MUSIC算法。该方法可以有效抑制DME干扰, 提高OFDM接收机性能。
Key words: L-band digital aeronautical communication system(LDACS) / distance measuring equipment(DME) / direction of arrival(DOA) estimation / improved single snapshot high order power(ISS-HOP) algorithm
关键字 : L波段数字航空通信系统 / 测距仪 / 波达方向估计 / 改进单快拍高阶幂算法
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
L波段数字航空通信系统是国际民航组织路线图中着重发展的未来地空数据链系统[1], 是未来航空宽带通信重要的基础设施之一。此外, LDACS还可为民航导航和监视提供备份解决方案, 发挥重要作用[2-3]。在信息安全方面, LDACS系统引入了危险评级, 提出了可行的网络安全架构和协议, 以减少地空通信消息交换所需的安全开销[4-6]。针对有限的、碎片化的频谱资源, 文献[7-9]提出了滤波正交频分复用(filtered orthogonal frequency division multiplexing, F-OFDM)、可重构F-OFDM、可变F-OFDM等波形设计方案, 功率谱密度更集中, 降低了带外泄露。测距仪DME与LDACS系统有部分频段重叠, 因此LDACS系统容易受到大功率DME信号的干扰, 严重影响LDACS系统OFDM接收机的性能[10]。
近年来, 许多研究致力于解决LDACS系统中DME干扰问题。在时域方面, 文献[11-13]研究了DME信号的数学模型, 并提出了脉冲熄灭和限幅等非线性时域滤波方法。随着性能要求的提高, 阵列天线已经应用于地空数据通信系统中, 通过选择不同的阵列可实现更高的信噪比和鲁棒性[14-15]。在阵列天线空域滤波方面, 文献[16-17]提出使用子空间正交投影抑制DME干扰的方法, 并通过盲波束形成将天线方向图的主瓣对准OFDM信号来向, 以提高输出信噪比。然而, 考虑到机载平台的机动特性, 可获得的快拍数目有限, 常规的盲波束形成方法和DOA估计方法将不再适用。Donoho、Malioutov和Candes等提出了关于稀疏信号采集和恢复的压缩感知理论, 为有限快拍下的DOA估计带来了新思路[18-20]。随着研究的不断深入, 利用单快拍样本间相关性质构造伪协方差矩阵的方法也被提出[21-22], 从而可以在单快拍时估计信号的方向。
针对LDACS系统中传统的DOA估计方法在单快拍时无法准确估计出OFDM信号入射方向的问题, 本文提出一种改进单快拍高阶幂ISS-HOP的DOA估计方法。首先, 接收机将接收信号矢量投影到干扰信号正交补空间消除DME干扰; 之后, 使用单快拍数据构造伪协方差矩阵, 求出伪协方差矩阵的高阶幂; 最后结合稀疏分解L1-SVD算法, 实现OFDM信号的DOA估计。
1 系统模型
本文提出的LDACS系统抗干扰接收机框图如图 1所示。接收机包括阵列天线、干扰抑制、DOA估计、波束形成、OFDM解调模块五部分。信号的处理流程为: 多个天线通道接收的信号先通过干扰抑制模块进行干扰抑制, 然后利用DOA估计模块估计出OFDM信号来向, 在OFDM来向上形成主波束, 充分利用阵列增益提高输出信噪比, 最后送入OFDM解调模块, 完成信号解调。本文重点关注干扰抑制和DOA估计。
设定机载接收天线为均匀线阵, 由M个阵元组成。接收信号包括LDACS系统的OFDM信号和DME干扰信号, 并且信号来自不同角度, 同时入射至均匀线阵, 且入射信号和噪声不相关。因此, 阵列接收信号矢量可表示为
式中: s(n)是OFDM信号; a(θ)是OFDM信号的导向矢量;jk(n)是第k个DME干扰;dk(θ)是第k个DME干扰对应的导向矢量;K是DME干扰的数目;n(n)是高斯白噪声。
(1) 式还可以表示为
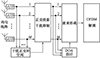 |
图1 LDACS抗干扰接收机 |
2 单快拍下的DOA估计方法
2.1 正交投影干扰抑制
考虑到OFDM信号、DME干扰、噪声彼此统计独立, 接收信号的协方差矩阵可表示为
式中:RS是OFDM信号的协方差矩阵; RJ是DME干扰的协方差矩阵; RN是噪声的协方差矩阵。
通过对协方差矩阵RXX进行分解可得
式中: λ1≥λ2≥…≥λK+1≥σK+22≥…≥σM2为协方差矩阵RXX的特征值, 并且特征值不为零; Ej为干扰子空间, Λj为对应特征值构成的对角矩阵; Es+n为OFDM信号与噪声子空间, Λs+n为对应特征值构成的对角矩阵。由于DME干扰的功率相比于OFDM信号和噪声大很多, 所以K个DME干扰对应的特征值λi(i=1, 2, …, K)明显大于其他特征值, 其对应的特征向量构成干扰子空间UJ。
通过对空间投影理论的分析, 利用干扰子空间得到其正交补空间为
阵列接收到的信号X(n)通过向UJ⊥投影, 能够抑制DME干扰, 过程为
阵列接收信号经过正交投影后得到的Y(n)用于DOA估计。
2.2 伪协方差矩阵的构造
采用单快拍接收信号并对其进行重新排列, 构造出秩与信源数目相等的伪协方差矩阵。构造矩阵的形式可以表示为
式中:D是L×L维满秩矩阵;L是信号数量; A(θ)=[a(θ1), a(θ2), …, a(θL)]是M×L维阵列流型矩阵。a(θl)中第p个元素可表示为ej[φl+(p-1)Δφl], 其中Δφl=(2πd/λ)sinθl。为确保伪协方差矩阵的秩与信源数目相等, 需要满足M>L, 则构造的伪协方差矩阵RZ的维度为M×M。
矩阵RZ的元素RZ(p, q)可表示为
式中, dmn为矩阵 D的元素。
当矩阵D为对角阵, 且对角线上的元素非0, 即m=n时, 矩阵 D是满秩的, (8)式可表示为
进而伪协方差矩阵RZ的秩为L, 可以表示为 RZ=A(θ)DAH(θ)。
在(9)式基础上, 令φm=0, dmm=sm, 则伪协方差矩阵可表示为[21]
2.3 ISS-HOP方法
根据第2.1节内容可知, 经过正交投影后的阵列接收信号仅包含OFDM信号和噪声, 并且OFDM信号的特征值大于噪声的特征值。
通过(10)式得到伪协方差矩阵, 分为两部分
对(11)式进行特征值分解得
对(12)式求m次高阶幂, 可以得到
(13) 式中的对角阵Σs=diag(λ1m, λ2m, …λLm), Σn=diag(σL+12m, σL+22m, …, σM2m), 其中L是OFDM信号个数。因为LDACS系统使用蜂窝网络通信, 在每个单元区域内通常只有一个OFDM信号, 所以取L=1。
因此通过高阶幂的计算, λ1m≫σ22m≥…≥σM2m, 在m趋于无穷大时, (13)式最后一项变为无穷小, 可忽略不计, 则(13)式可表示为
在实际情况中, 参数m无需取极限值, 绝大多数情况下取有限整数就能满足需求。
为了单快拍时能够准确估计出OFDM信号的入射方向, 构造出高阶伪协方差矩阵代替常规协方差矩阵, 然后利用稀疏分解L1-SVD方法估计信号的波达方向。具体的步骤为:
步骤1 利用(10)式获得伪协方差矩阵RZ;
步骤2 对伪协方差矩阵求m次幂得到高阶伪协方差矩阵RZm;
步骤3 对伪协方差矩阵的高阶幂RZm进行奇异值分解;
步骤4 扩展方向向量, 构建冗余字典, 并建立稀疏模型;
步骤5 针对稀疏模型, 采用二阶锥规划方法求最优解。
3 验证与分析
3.1 仿真参数设置
根据LDACS系统技术规范[23], 设计LDACS仿真系统实现基于高阶幂的单快拍DOA估计。表 1所示为LDACS系统的仿真技术参数。
其他的实验参数设置为: 阵列天线采用均匀线阵, 阵元数目为16个, 相邻2个阵元间距为信号半波长; OFDM信号来向设置为10°, DME干扰信号来向为30°, 噪声为加性高斯白噪声; 信噪比和信干比设置分别为10 dB和-10 dB。
实验中为了衡量DOA估计的准确程度, 引入均方根误差(RMSE), 计算方法为
式中: K表示信号个数; NMC表示蒙特卡洛实验的仿真次数; 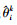 表示第i次蒙特卡洛实验中第k个信号的DOA估计角度; θik表示第i次蒙特卡洛实验中第k个信号的真实角度。
表示第i次蒙特卡洛实验中第k个信号的DOA估计角度; θik表示第i次蒙特卡洛实验中第k个信号的真实角度。
LDACS系统的仿真技术参数
3.2 仿真实验与分析
在实验过程中, 除了本文提到的稀疏分解L1-SVD方法, 还使用了MUSIC算法进行对比实验。图 2显示了在单快拍情况下, 4种DOA估计方法的空间谱结果。可以看出, 正交投影抑制DME干扰后的接收信号, 使用常规MUSIC算法和L1-SVD算法, 空间谱杂乱, 无法准确分辨出目标角度。而构造伪协方差矩阵并进行高阶幂运算, 即ISS-HOP算法, 所得到的空间谱尖锐, 只有一个峰值, 对应OFDM信号的入射方向。这表明单快拍情况下, ISS-HOP算法具有可行性, 能够准确估计期望信号来向, 而且本文提出的ISS-HOP-L1-SVD算法谱峰更尖锐, 分辨性能更好。
图 3显示多快拍情况下, 常规DOA估计的空间谱结果。设置快拍数为200, 信号来向等其他设置不变。可以看出, 利用正交投影抑制掉DME干扰后, MUSIC算法和稀疏分解L1-SVD算法的空间谱只有1个峰值, 且峰值对应的角度即为OFDM信号的入射方向。
为了进一步探究快拍数对DOA估计误差性能的影响, 将接收信号的快拍数范围设置为20~150, 步长为10, 并进行300次蒙特卡洛实验。图 4显示了2种算法的均方根误差随快拍数变化情况, 从仿真结果中可以看出, 随着快拍数的增加, 估计误差逐渐减小, 当快拍数增加到80之后, 2种方法的估计误差能够保持在较低的水平, 并趋向于0。这表明只有在快拍数较多时常规的DOA估计算法才具有良好的估计性能。
为研究基于高阶幂的单快拍DOA估计算法性能, 将快拍数设置为单快拍, 在信噪比从-5~5 dB以1 dB间隔变化的条件下, 进行300次蒙特卡洛仿真实验。图 5的实验结果显示, 无高阶幂运算的ISS算法和有高阶幂运算的ISS-HOP算法的均方根误差随着SNR的增加呈现下降趋势, 并在3 dB左右接近于零, 但ISS-HOP算法通过对伪协方差矩阵进行高阶幂运算, 能够减小噪声的影响, 因此其信噪比适应能力比ISS算法更好。4种算法中, ISS-HOP-L1-SVD算法的RMSE最小, 当信噪比为0 dB时, 均方根误差小于1°, 估计性能比其他的3种方法更好。
 |
图2 单快拍情况下的空间谱 |
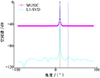 |
图3 多快拍情况下的空间谱 |
 |
图4 不同快拍数情况下的RMSE性能 |
 |
图5 不同信噪比情况下的RMSE性能 |
4 结论
针对DME信号对LDACS系统造成干扰, 导致OFDM接收机性能受到严重影响的问题, 本文提出了一种基于高阶幂的单快拍LDACS系统信号来向估计方法。首先OFDM接收机通过子空间投影方法得到干扰信号的正交补空间, 抑制DME信号获得无干扰数据, 然后在DOA估计器中, 利用单快拍数据构建伪协方差矩阵并进行高阶幂运算, 最后结合稀疏分解特性形成ISS-HOP-L1-SVD算法, 在单快拍情况下实现准确的DOA估计。本方法能够解决常规DOA估计方法在单快拍下失效的问题, 使用高阶伪协方差矩阵不仅确保了较好的估计效果, 同时还降低了噪声影响, 减小估计误差。在仿真实验中, ISS-HOP-L1-SVD算法的误差性能要优于ISS-HOP-MUSIC算法。实验结果表明, 所提出的方法可以有效地消除LDACS系统中的DME干扰, 提高系统的性能和可靠性。在未来的研究中, 可以进一步探索其他单快拍算法在该问题上的应用, 以提高DOA估计的性能。
References
- SCHNELL M, EPPLE U, SHUTIN D, et al. LDACS: future aeronautical communications for air-traffic management[J]. IEEE Communications Magazine, 2014, 52(5): 104–110. [Article] [CrossRef] [Google Scholar]
- BATTISTA G, KUMAR R, NOSSEK E, et al. Placing LDACS-based ranging sources for robust RNP 1.0 accuracy en-route[C]//IEEE/AIAA 36th Digital Avionics Systems Conference, St. Petersburg, USA, 2017 [Google Scholar]
- FILIP-DHAUBHADEL A, SHUTIN D. LDACS-based non-cooperative surveillance multistatic radar design and detection cover-age assessment[C]//IEEE/AIAA 38th Digital Avionics Systems Conference, San Diego, USA, 2019 [Google Scholar]
- MÄURER N. Paving the way for an IT security architecture for LDACS: a datalink security threat-and risk analysis[C]//Integrated Communications, Navigation, Surveillance Conference, Herndon, USA, 2018 [Google Scholar]
- MÄURER N, GRÄUPL T, SCHMITT C. Evaluation of the LDACS Cybersecurity Implementation[C]//IEEE/AIAA 38th Digital Avionics Systems Conference, San Diego, USA, 2019 [Google Scholar]
- EWERT T, MÄURER N, GRÄUPL T. Improving usable LDACS data rate via certificate validity optimization[C]//Integrated Communication, Navigation and Surveillance Conference, Dulles, USA, 2022 [Google Scholar]
- ABD-ELATY E, EL-AGOOZ S, ZEKRY A. Compact spread spectrum LDACS wavelet based for DME interference mitigation[C]//National Radio Science Conference, Port Said, Egypt, 2019 [Google Scholar]
- AGRAWAL N, AMBEDE A, DARAK S J, et al. Design and implementation of low complexity reconfigurable filtered-OFDM-based LDACS[J]. IEEE Trans on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(7): 2399–2403. [Article] [CrossRef] [Google Scholar]
- ROY S, CHANDRA A. On the design of variable Filtered-OFDM based LDACS for future generation air-to-ground communication system[J]. IEEE Trans on Circuits and Systems Ⅱ: Express Briefs, 2022, 69(2): 644–648. [Article] [CrossRef] [Google Scholar]
- FANTAPPIE P. L-DACS spectral efficiency[C]//Integrated Communications, Navigation and Surveillance Conference, Herndon, USA, 2019 [Google Scholar]
- EPPLE U, BRANDES S, GLIGOREVIC S, et al. Receiver optimization for L-DACS1[C]//IEEE/AIAA 28th Digital Avionics Systems Conference, Orlando, USA, 2009 [Google Scholar]
- EPPLE U, SHUTIN D, SCHNELL M. Mitigation of impulsive frequency-selective interference in OFDM based systems[J]. IEEE Wireless Communications Letters, 2012, 1(5): 484–487. [Article] [CrossRef] [Google Scholar]
- EPPLE U, SCHNELL M. Adaptive threshold optimization for a blanking nonlinearity in ofdm receivers[C]//Global Communications Conference, Anaheim, USA, 2012 [Google Scholar]
- RAO S, PANDYA A, OSTROOT C. Phased array antennas for aircraft applications[C]//IEEE Indian Conference on Antennas and Propogation, Hyderabad, India, 2018 [Google Scholar]
- GVRBVZ A, MIELKE D M, BELLIDO-MANGANELL M A. On the Application of beamforming in LDACS[C]//Integrated Communication, Navigation and Surveillance Conference, Dulles, USA, 2022 [Google Scholar]
- WANG Lei, LI Guangxue, LI Dongxia, et al. Interference suppression and blind beamforming based on OFDM symbol characteristic[J]. Control and Decision, 2020, 35(6): 1397–1402. [Article] (in Chinese) [Google Scholar]
- WANG Lei, SUN Haixia, LIU Mingli, et al. Signal direction estimation method for wideband aeronautical data link system based on signal characteristics[J]. Journal of Signal Processing, 2022, 38(7): 1458–1466. [Article] (in Chinese) [Google Scholar]
- DONOHO D L. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4): 1289–1306. [Article] [CrossRef] [Google Scholar]
- MALIOUTOV D, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Trans on Signal Processing, 2005, 53(8): 3010–3022. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- CANDES E J, ROMBERG J K, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. [Article] [CrossRef] [Google Scholar]
- XIE Xin, LI Guolin, LIU Wenhua. DOA estimation of coherent signals using one snapshot[J]. Journal of Electronics & Information Technology, 2010, 32(3): 604–608. [Article] (in Chinese) [CrossRef] [Google Scholar]
- JIANG Baifeng, LYU Xiaode, XIANG Maosheng. Single snapshot DOA estimation method based on rearrangement of array receiving signal[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1334–1339. [Article] (in Chinese) [Google Scholar]
- EUROCONTROL. PJ. 14-W2-60 TRL6 Final LDACS A/G Specification[EB/OL]. (2023-03-10)[2023-04-08]. [Article] [Google Scholar]
All Tables
All Figures
 |
图1 LDACS抗干扰接收机 |
| In the text | |
 |
图2 单快拍情况下的空间谱 |
| In the text | |
 |
图3 多快拍情况下的空间谱 |
| In the text | |
 |
图4 不同快拍数情况下的RMSE性能 |
| In the text | |
 |
图5 不同信噪比情况下的RMSE性能 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


