| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 460 - 466 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230460 | |
| Published online | 01 October 2024 | |
State estimation of variable frequency power grid of multi-electric aircraft based on adaptive enhanced complex-coefficient filter
基于自适应增强型复系数滤波器的多电飞机变频电网状态估计
1
College of Energy and Electrical Engineering, Chang'an University, Xi'an 710064, China
2
School of Automation, Northwestern Polytechnical University, Xi'an 710129, China
Received:
25
May
2023
The power grid of a multi-electric aircraft is a typical isolated island microgrid with a wide frequency range from 360 to 800 Hz. The dynamic performance of the traditional constant-frequency power grid synchronization method is insufficient in the variable frequency power grid of the multi-electric aircraft. An adaptive enhanced complex-coefficient filter-based phase locked loop (AECCF-PLL) is designed for the variable frequency power grid by integrating an adaptive module into the enhanced complex-coefficient filter-based phase locked loop to accurately estimate the state of variable frequency power grid. The relationship between the transfer function and the step response is analyzed. The relationship between the model parameters and the frequency is derived, and the frequency adaptive module is established to meet the requirements for stability and rapidity in the state estimation of the variable frequency power grid. The experimental results show that the proposed AECCF-PLL can achieve the rapid and stable estimation of the state of the variable frequency power grid when there are disturbances such as large or small frequency jumps, harmonics and slopes.
摘要
多电飞机的电网是一种典型的孤岛微网, 具有360~800 Hz的宽频率工作范围, 传统恒定频率电网同步方法的动态性能在飞机变频电网中有所不足。为了准确估计飞机变频电网的电网状态, 结合自适应模块, 对增强型复系数滤波器锁相环进行改进, 设计了一种适应于MEA变频电网的自适应增强型复系数滤波器锁相环结构(AECCF-PLL)。分析了其传递函数与阶跃响应之间的关系, 推导了模型参数与频率的关系, 建立了频率自适应模块, 满足飞机变频交流电网状态估计对稳定性和快速性的要求。实验结果表明, 在飞机变频电网含有大小频率跳变、谐波、斜坡等扰动情况时, 提出的AECCF-PLL可以实现对电网状态的快速稳定估计。
Key words: variable frequency power grid / grid synchronization / adaptive frequency / phase locked loop
关键字 : 变频电网 / 电网同步 / 频率自适应 / 锁相环
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
与传统飞机相比, 多电飞机(MEA)具有质量轻、可靠性高、损耗低的优势, 受到了越来越多的关注, 成为航空技术的发展趋势[1]。随着电力系统和电网容量的增加, MEA中的拓扑、控制和参数估计等电网技术的研究越来越重要。在MEA技术中, 电网电压参数的估计为电力系统提供了关键信息, 频率和相位的估计对于MEA电网的功率控制和电网同步必不可少。MEA电网是典型的孤岛微网, 具有360~800 Hz的宽频率范围, 从一个正常频率瞬变开始, 在大于25 ms时段测量的频率变化率应不大于250 Hz/s, 但随着不同功能的需求, 频率会进行大范围跳变, 超过了正常频率波动变化率, 条件更加苛刻, 因此对其状态估计方法提出了一个更高的要求[2]。工频电网具有恒定频率, 相比之下, 在MEA电网中估计频率和相位比在工频电网中的难度更加提高[3]。
目前许多学者已经提出了多种用于工频电网交流系统的电网电压参数估计方法。主要方法有卡尔曼滤波[4–5]、离散傅里叶变换[6–7]、过零检测[8]、自适应陷波滤波器[9–10]、最小二乘估计和锁相环(PLL)[11–14]。估计参数通常包括电网频率和相位。在这些估计方法中, PLL因为结构简单且性能良好, 是最常用的估计公用电网电压参数的方法。单同步参考坐标系锁相环(SSRF-SPLL)作为电网同步的一种经典方法, 经常用于公用电网的参数估计[15]。但PLL锁相后会出现2倍频振荡, 影响检测精度和性能, 因此需要改进锁相环来提高检测精度和性能[16]。文献[16]提供了基于双二阶广义积分器和解耦双同步参考坐标系的锁相环方法, 适应于基频不对称电网故障下的电网同步。文献[17]研究了一种基于广义DFT的同步参考帧锁相环, 来提高基频电网抑制谐波的能力。文献[18]中复系数滤波器锁相环(CCF-PLL)能够选择性地提取/抑制不同信号的干扰, 提高在基频下的抗干扰能力, 但PLL的VCO输入到CCF之间存在一个频率反馈环路, 导致它们之间的动态相互作用, 使动态响应较差。为了提高该锁相环的性能, 文献[19]中提出了ECCF-PLL, 对文献[18]中的频率反馈信息进行改变, 避免了动态交互, 并不添加额外的计算负担。这些适用在工频电网下的锁相环方法, 在MEA变频电网下将远离平衡点工作, 性能显著下降[20]。因此一些学者针对MEA变频电网, 提出了一些改进方案。在文献[21]中, 通过增加重复观测器(RO)增强线性卡尔曼滤波器PLL的抗扰能力。在文献[22]中, 提出了一种基于自适应观测器的多正弦信号鲁棒估计的方法, 以便提高飞机电网同步的动态响应。
本文首先分析了典型SSRF-SPLL在工频电网下能有效应对电网小频率跳变时追踪频率和相位的情况, 但在变频电网频率跳变时可能会远离平衡点工作, 动态性能可能有所损失。针对此问题, 结合自适应模块和增强型复系数滤波器锁相环(ECCF-PLL)[23], 设计了一种适应于MEA变频电网的自适应增强型复系数滤波器锁相环结构(AECCF-PLL)。先阐述AECCF-PLL的工作原理, 后给出了AECCF-PLL中的参数设计方法。最后, 通过实验结果验证了设计的AECCF-PLL在变频电网下含有大小频率跳变、谐波、斜坡时, 均可以实现对电网电压信息稳定快速精确的估计。
1 典型锁相环的分析
典型锁相环(SSRF-SPLL)的结构图如图 1所示, 包含3个基本模块: 相角检测器(PD)、环路滤波器(LF)和电压控制振荡器(VCO)。
根据文献[18], SSRF-SPLL中相角估计的闭环误差传递函数为
kp, ki为比例积分器的系数。由经典控制理论可知SSRF-SPLL以恒定频率应用于公用电网时, 它在其平衡点附近工作, 在稳态精度和动态响应方面都具有良好的性能。当电网电压的频率大范围变化时, 假设电网电压的频率变化Δωin在电网频率ωc-ΔωL和ωc+ΔωL之间, SSRF-SPLL具有快速的动态响应, 其中PI环路滤波器的锁定范围ΔωL近似为
阻尼系数ξ取最佳阻尼比为1/ 2, 其锁定时间TL计算为
如果频率变化Δωin超出范围ωc ±ΔωL, 但落在SSRF-SPLL总能牵引进入锁相状态的牵入范围ΔωP内, 则锁相环所需的锁相时间为
会使PLL的动态响应变得非常慢。总之, 在电网频率小范围内变化的工频电网中, PLL在ωc ±ΔωL范围内运行, 具有良好的动态响应。然而, 频率范围在360~800 Hz之间的MEA变频电网中, 锁相环可能在ωc ±ΔωL范围外工作, 因此其动态性能显著下降。
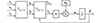 |
图1 单同步参考坐标系锁相环(SSRF-SPLL)结构图 |
2 增强型复系数滤波器锁相环
ECCF-PLL的结构图如图 2所示。ECCF-PLL使用2个复系数带通滤波器以协作的方式提取基频正负序分量, 同时为了避免电压控制振荡器(VCO)和频率反馈之间的动态交互, 将传统PLL估计频率的输出改为VCO的输入加上PI控制器中的积分器的输出来提供电网频率的估计, 将该频率估计值用于反馈到滤波器的信号, 将改进的PLL结构来检测基频正序分量的参数。
将模型线性化可得到ECCF-PLL的传递函数为
复系数滤波器具有序列选择性滤波能力, 使ECCF-PLL能够在PLL控制回路之前有效抑制谐波扰动, 而为了避免动态交互后改进的PLL结构, 使ECCF-PLL在基频电网下可以获得较好的动态性能和鲁棒性。但在MEA变频电网大范围频率变化下, 锁相环可能在ωc±ΔωL范围外工作, 系统的动态响应降低。
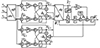 |
图2 增强型复系数滤波器锁相环(ECCF-PLL)结构图 |
3 变频电网自适应增强型复系数滤波器锁相环
为了提高锁相环在MEA变频电网下的动态性能, 使频率变化Δωin落在ωc±ΔωL范围, 提出了AECCF-PLL, 该模型将锁相环输出的电网频率反馈给复系数滤波器中的截止频率ωp和锁相环中PI控制器的比例系数kp与积分系数ki, 使模型参数随电网频率变化来实时修正, 从而构成自适应的复系数滤波器和自适应的锁相环。提出的AECCF-PLL结构如图 3所示, 使用2个自适应的复带通滤波器提取频率的正负序分量, 使用PI自适应的PLL检测频率正序分量的频率和相位。
由复系数滤波器的传递函数[20]可知截止频率ωp决定了传递函数的阻尼因子。通常二阶系统采用的最佳阻尼系数为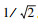 。在自适应增强型复系数滤波器中, 截止频率ωp对应于
。在自适应增强型复系数滤波器中, 截止频率ωp对应于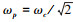 , ωc表示在MEA变频电网下实时变化输出的电网频率。
, ωc表示在MEA变频电网下实时变化输出的电网频率。
将(5)式中的特征多项式与三阶系统的单位阶跃响应联立可得
展开(6)式中对应系数可得
由(7)~(8)式联立可得
根据二次函数判别性质(由于比例增益kp只能具有实数值(相对于复数来说), 因此二次方程(10)的判别式应该大于或等于0), 结合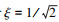 和
和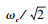 可得
可得
μ是根据固有频率值确定实际极点位置的系数, 由(10)式中二次函数判别式可知, μ不受ωp值的影响, 为保持锁相环的高滤波能力, 实际极点位置应尽可能靠近原点,即选择μ的最小可能值ωp=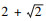 代入(7)~(9)式, 可得出AECCF-PLL中ωp, kp, ki三者与电网频率ωc(等同于模型结构图中的
代入(7)~(9)式, 可得出AECCF-PLL中ωp, kp, ki三者与电网频率ωc(等同于模型结构图中的 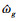 )之间的关系式。
)之间的关系式。
由(13)~(15)式可知变化的电网频率与模型参数之间关系式, 在MEA变频电网下AECCF-PLL的自适应复系数滤波器的截止频率ωp会随着频率ωc的变化而变化, 从而影响系统的带宽; 电网频率ωc变化的同时, 也会改变自适应PI中kp, ki的值, 随之改变ΔωL的值, 使频率变化Δωin落在ωc±ΔωL范围, 以获得较好的动态响应。
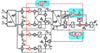 |
图3 自适应增强型复系数滤波器锁相环(AECCF-PLL)结构图 |
4 实验
在本节中, 将设计的AECCF-PLL与ECCF-PLL、SSRF-SPLL进行对比。实验装置如图 4所示。使用基于DSP TMS320C28346的RTU-BOX平台。
实验参数设置如表 1所示。
 |
图4 实验装置 |
实验参数表
4.1 小频率跳变
为验证AECCF-PLL在MEA电网小频率跳变下的跟踪性能, 电网电压频率从450 Hz跳变为460 Hz。图 5a)为输入信号, 图 5b)为3种锁相环在进行小频率跳变时对电网频率估计的结果, 在发生小频率跳变时, 所提出的AECCF-PLL可以在9 ms内准确估计电网频率, 其动态响应速度快于ECCF-PLL、SSRF-SPLL。图 5c)为3种锁相环估计的相位误差, 其中AECCF-PLL的相位误差收敛于零, 另外2种锁相环均含有静差, 得出AECCF-PLL在450 Hz的小频率跳变下具有更短的稳定时间和更高的稳定性。
 |
图5 电网频率发生小频率跳变450~460 Hz的实验结果 |
4.2 大频率跳变
为验证AECCF-PLL在MEA电网大频率跳变下跟踪性能, 电网电压频率从450 Hz跳变为750 Hz。图 6b)为3种锁相环在450 Hz时进行大频率跳变对电网频率估计的结果, 可以看出所提出的AECCF-PLL可以在8 ms内准确估计电网频率, SSRF-SPLL不稳定震荡, AECCF-PLL具有更短的稳定时间和更平滑的动态行为。从图 6c)可以看出AECCF-PLL短暂震荡后趋近于零的相位误差, 其他两者均有持续震荡。综合对比看出AECCF-PLL在MEA电网大频率跳变时, 有较好的动态响应。
 |
图6 电网频率发生大频率跳变450~750 Hz的实验结果 |
4.3 谐波
为验证AECCF-PLL对于谐波抑制的效果, 为450 Hz频率施加谐波分量, 谐波分量中含有5, 7, 11次谐波, 其中V5=0.1 p.u., V7=0.1 p.u., V11=0.1 p.u.。3种锁相环对于谐波抑制的效果如图 7所示, 图 7a)为输入信号, 图 7b)为3种锁相环在频率不发生变化时施加谐波对电网频率估计的结果, 可以看出在谐波下SSRF-SPLL对电网频率的估计含有持续震荡, 效果较差, AECCF-PLL有极小的震荡, 估计频率的稳态误差为0.097%, 效果好于SSRF-SPLL, 略低于ECCF-PLL。图 7c)为3种锁相环估计的相位误差, 三者的相位误差均收敛于零, 可知AECCF-PLL和ECCF-PLL对谐波抑制有较好的效果。
 |
图7 电网电压中含有5, 7, 11次谐波的实验结果 |
4.4 斜坡
为验证AECCF-PLL对于MEA电网频率斜坡变化的跟踪效果, 输入电网电压频率为450~750 Hz的斜坡变化。图 8a)为3种锁相环对电网频率估计的对比, 可以看出AECCF-PLL、ECCF-PLL在对频率追踪的过程中, 具有平滑的动态行为, AECCF-PLL达到近乎零误差的频率追踪, ECCF-PLL追踪频率有明显延迟, 图 8b)可以看出ECCF-PLL在斜坡变化时, 有持续的稳态误差, SSRF-SPLL持续震荡波动, AECCF-PLL保持零稳态误差。综合看出AECCF-PLL在频率斜坡变化追踪时, 有更好的稳定性。
表 2~3提供了3种锁相环在不同情况下的动态性能总结。SSRF-SPLL在变频电网中不稳定, 多数情况下会一直出现震荡, 数据较少, 出现震荡时在表中用“/”来表示。
 |
图8 电网频率出现斜坡(450~750 Hz)变化的实验结果 |
不同方法的性能比较
不同方法的性能比较
5 结论
本文提出了一种自适应增强型复系数滤波器锁相环(AECCF-PLL), 用于MEA变频电网状态估计。与ECCF-PLL和SSRF-SPLL相比, 该方法通过建立频率反馈自适应模块, 使模型参数随电网频率变化实时修正, 该方法在大小频率跳变、斜坡和谐波情况下都可以较快且稳定地估计出电网状态。本文给出了详细的参数设计方法, 最后通过对比实验结果, 验证了设计的AECCF-PLL在应对MEA变频电网故障时, 具备了良好的参数状态估计准确性。
References
- MADONNA V, GIANGRANDE P, GALEA M. Electrical power generation in aircraft: review, challenges, and opportunities[J]. IEEE Trans on Transportation Electrification, 2018, 4(3): 646–659 [Article] [CrossRef] [Google Scholar]
- DAI Z, LV S, MWANIKI J K, et al. Global accurate estimation of positive-and negative-sequence voltage components for variable frequency AC systems[J]. IET Power Electronics, 2018, 11(10): 1730–1737 [Article] [CrossRef] [Google Scholar]
- FAN M, DAI Z, YANG Y, et al. Fast grid synchronization method for variable-frequency AC systems[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 105990 [CrossRef] [Google Scholar]
- NIE X. Detection of grid voltage fundamental and harmonic components using Kalman filter based on dynamic tracking model[J]. IEEE Trans on Industrial Electronics, 2020, 67(2): 1191–1200 [Article] [CrossRef] [Google Scholar]
- XU W, HUANG C, GOLESTAN S. Design-oriented study of the orthogonal vector-based linear Kalman filter: enhancements and applications[J]. IEEE Trans on Industrial Electronics, 2022, 69(12): 13359–13372 [Article] [CrossRef] [Google Scholar]
- LI Hai, YANG Xiaoliu. Design of a new fast phase locked loop based on adaptive sliding mode observer[J]. Journal of power Sources, 2021, 19(5): 143–149 [Article] (in Chinese) [Google Scholar]
- XU Z, DAI K, YANG B, et al. Three-phase PLL based on vector dft under distorted and unbalanced grid[C]//2022 IEEE 3rd China International Youth Conference on Electrical Engineering, Wuhan, 2022: 8881–8891 [Google Scholar]
- REZA M S, SADEQUE F, HOSSAIN M M, et al. Three-phase PLL for grid-connected power converters under both amplitude and phase unbalanced conditions[J]. IEEE Trans on Industrial Electronics, 2019, 66(11): 8881–8891 [Article] [CrossRef] [Google Scholar]
- HE X, GENG H, YANG G. A generalized design framework of notch filter based frequency-locked loop for three-phase grid voltage[J]. IEEE Trans on Industrial Electronics, 2018, 65(9): 7072–7084 [Article] [CrossRef] [Google Scholar]
- ZHANG Q, FAN Y, CHEN J, et al. A current harmonic suppression method for PMSM based on harmonic prediction adaptive notch filter[J]. IEEE Trans on Energy Conversion, 2022, 37(3): 2107–2118 [Google Scholar]
- WANG Xubin, DU Wenjuan, WANG Haifeng. Review of stability analysis of grid-connected VSC systems with weak connections[J]. Proceedings of the Chinese Society for Electrical Engineering, 2018, 38(6): 1593–1604 [Article] (in Chinese) [Google Scholar]
- HU Qi, FU Lijun, MA Fan, et al. Small disturbance synchronous stability analysis of grid-connected converter based on phase-locked control in weak current network[J]. Proceedings of the Chinese Society for Electrical Engineering, 2021, 41(1): 98–108 [Article] (in Chinese) [Google Scholar]
- HASSAN F, KUMAR A, PATI A. Recent advances in phase locked loops for grid connected systems: a review[C]//2022 IEEE Delhi Section Conference, New Delhi, India, 2022: 1–6 [Google Scholar]
- BABU B C. A novel adaptive bandpass filter based pll for grid synchronization under distorted grid conditions[J]. IEEE Trans on Instrumentation and Measurement, 2022, 711–11 [NASA ADS] [Google Scholar]
- ZHANG Xing, ZHANG Chongwei. PWM rectifier and its control[M]. Beijing: China Machine Press, 2012 (in Chinese) [Google Scholar]
- TEODORESCU R, LISERRE M, RODRIGUEZ P. Grid converters for photovoltaic and wind power systems[M]. ZHOU Keliang, WANG Zheng, XU Qingshan, Translated, Beijing: China Machine Press, 2012 (in Chinese) [Google Scholar]
- YANG T, LU D, XING Y, et al. Generalized DFT-based synchronous reference frame phase-locked loop applicable to distorted grid conditions[C]//IEEE International Power Electronics and Motion Control Conference, Gliwice, Poland, 2021: 319–324 [Google Scholar]
- DAI Z, YANG J, RAO D, et al. A global convergence estimator of grid voltage parameters for more electric aircraft[J]. IEEE Trans on Industrial Electronics, 2020, 67(9): 7540–7549 [Article] [CrossRef] [Google Scholar]
- GUO X, WU W, CHEN Z. Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]. IEEE Trans on Industrial Electronics, 2011, 58(4): 1194–1204 [Article] [CrossRef] [Google Scholar]
- RAMEZANI M, GOLESTAN S, LI S, et al. A simple approach to enhance the performance of complex-coefficient filter-based PLL in grid-connected applications[J]. IEEE Trans on Industrial Electronics, 2018, 65(6): 5081–5085 [Article] [CrossRef] [Google Scholar]
- TANG M, BIFARETTI S, PIPOLO S, et al. A novel low computational burden dual-observer phase-locked loop with strong disturbance rejection capability for more electric aircraft[J]. IEEE Trans on Industry Applications, 2021, 57(4): 3832–3841 [CrossRef] [Google Scholar]
- CHEN B, PIN G, NG W M, et al. An adaptive observer-based robust estimator of multi-sinusoidal signals[J]. IEEE Trans on Automatic Control, 2018, 63(6): 1618–1631 [CrossRef] [Google Scholar]
- RAMEZANI M, GOLESTAN S, LI S, et al. A simple approach to enhance the performance of complex-coefficient filter-based PLL in grid-connected applications[J]. IEEE Trans on Industrial Electronics, 2018, 65(6): 5081–5085 [CrossRef] [Google Scholar]
All Tables
All Figures
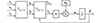 |
图1 单同步参考坐标系锁相环(SSRF-SPLL)结构图 |
| In the text | |
 |
图2 增强型复系数滤波器锁相环(ECCF-PLL)结构图 |
| In the text | |
 |
图3 自适应增强型复系数滤波器锁相环(AECCF-PLL)结构图 |
| In the text | |
 |
图4 实验装置 |
| In the text | |
 |
图5 电网频率发生小频率跳变450~460 Hz的实验结果 |
| In the text | |
 |
图6 电网频率发生大频率跳变450~750 Hz的实验结果 |
| In the text | |
 |
图7 电网电压中含有5, 7, 11次谐波的实验结果 |
| In the text | |
 |
图8 电网频率出现斜坡(450~750 Hz)变化的实验结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


