| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 467 - 476 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230467 | |
| Published online | 01 October 2024 | |
The multi-stage adding strategy on Kriging and applied to cavitation optimization of centrifugal impeller
基于Kriging的多阶段加点策略及离心叶轮汽蚀优化
1
School of Power and Energy, Northwestern Polytechnical University, Xi'an 710072, China
2
School of Construction Machinery, Chang'an University, Xi'an 710064, China
3
AECC Hunan Power-Plant Research Institute, Zhuzhou 412002, China
Received:
12
April
2023
In order to realize the intelligent optimization design of cavitation performance of fuel centrifugal pump, a multi-stage active learning adding strategy based on Kriging is proposed. The focus is to establish the three-stage adding strategy by using MSE, EI and CV, and clarify the switching criteria for each stage. Based on the test functions such as one-dimensional function and multi-dimensional function, it is compared with the single-stage adding strategy to verify the effectiveness of the proposed strategy. Furthermore, for a certain type of fuel centrifugal pump, the optimization application of the proposed strategy in its cavitation characteristics is completed. The result of the test function calculation shows that the proposed strategy takes slightly longer to achieve the same accuracy than MSE, which is better than EI and CV. However, compared with MSE, the local accuracy of the global optimal solution is higher. The result of centrifugal pump case shows that the pressure loss at the inlet of the optimized pump decreases, the local flow such as return flow and vortex at the inlet is weakened, the pressure gradient and the vortex flow in the volute weakens. Moreover, the cavitation coefficient of the optimized pump is increased by 30.83%, the NPSH allowance is reduced by 9.14%, the cavitation ratio is reduced by 7.17%, and the gas content in the pump is reduced by 17.27%. Thus, the proposed method improves the cavitation performance of the centrifugal pump effectively.
摘要
为了实现燃油离心泵汽蚀特性智能优化设计, 提出一种基于Kriging的多阶段主动学习加点策略。重点是建立3个阶段的加点策略, 并明确各阶段加点策略的切换判据。基于一维函数、多维函数等测试函数, 与单加点策略对比以验证多阶段主动学习加点策略的有效性。进而, 以某型燃油离心泵为例, 完成所提出加点策略在其汽蚀特性的优化应用。测试函数算例结果表明: 多阶段主动学习加点策略达到相同精度所需时间稍长于单MSE策略, 优于单EI策略与单CV策略; 但相比单MSE策略, 全局最优解局部精度更高。离心泵汽蚀特性优化结果表明: 优化泵进口处压力损失降低且进口处回流、旋涡等局部流动减弱, 蜗壳内压力梯度增大且其出口处旋涡流动减弱; 优化泵的汽蚀系数提高30.83%, 汽蚀余量下降9.14%, 汽蚀比转数下降7.17%, 泵内气体含量下降17.27%, 所提出的方法有效地提高了离心泵的抗汽蚀性能。
Key words: aero-fuel centrifugal pump / cavitation performance / Kriging modeling / adding strategy / optimization design
关键字 : 燃油离心泵 / 汽蚀特性 / Kriging / 加点策略 / 优化设计
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
为了实现高压、高效、高可靠性及长寿命航空发动机燃油系统的技术发展目标, 对其各组件进行性能提升至关重要。其中, 作为系统增压泵、加力泵的燃油离心泵, 亦需深入探讨并研究其综合性能[1–2]。尤其是在当前大机动飞行、超声速巡航的工作要求下, 离心泵内存在复杂的汽蚀流动问题, 制约着泵的增压效率, 严重时影响着泵的寿命及可靠性。因此, 很有必要研究一种高效的离心泵汽蚀特性优化方法[3–4]。
目前, 对离心泵汽蚀优化的相关研究普遍基于全三维计算流体力学(computational fluid dynamics, CFD), 将湍流模型和两相模型结合以求解泵内的气液分布, 进而对叶轮几何参数、型线参数不断迭代完成汽蚀优化设计[5–6]。但这种方法对专家经验依赖性较强,且无法获取离心泵在全工况下最优的抗汽蚀特性。同时, 航空发动机燃油离心泵自身运行工况特殊、运行边界复杂且运行环境严酷, 使得离心泵的几何参数、型线参数以及汽蚀相关的流动参数之间的相互影响更加复杂、非线性更强, 共同耦合决定泵的综合性能[7]。然而, 在泵实际设计过程中上述3类参数尚无法建立基于模型的解析解, 因此, 传统的设计方法无法针对性地实现汽蚀优化设计, 所消耗计算成本较高、设计效率较低[8], 极有必要针对燃油离心泵汽蚀特性开展高效、智能化的优化设计研究。当前, 随着计算机技术的发展, 计算流体力学、数据驱动方法以及主动学习策略等越来越完善, 更多智能的数据驱动建模方法及其在旋转机械的优化设计应用已成为了研究热点、重点[9–10]。通过调用计算流体力学参数化计算结果, 采用代理模型的方法建立优化变量与优化目标的显性关系, 从而快速、高效地实现多目标优化[11]。这一方法能够有效提高优化效率和智能程度, 充分挖掘离心泵的抗汽蚀特性。在这一趋势下, 越来越多的科研人员对离心泵相关性能的智能优化方法开展了研究。
离心泵汽蚀特性的优化研究主要涉及了基于CFD迭代的优化设计、基于数据驱动的代理模型优化设计等方面。罗云霞[12]为了抑制泵内汽蚀的进一步扩展, 研究了前缘开缝叶片对离心泵汽蚀特性及内部流场结构的影响规律。赵伟国等[13]在叶轮前盖板内表面布置非连通形式的小叶片, 分析汽蚀特性的影响规律, 并给出优化建议。陈冰等[14]以某型离心泵为例, 对其内部流动进行了数值计算及汽蚀特性模拟, 预测设计点的临界汽蚀余量, 并对叶轮的结构参数进行了优化设计, 从而提高了泵的抗汽蚀性能。可见, 离心叶轮不同的几何参数、结构形式对泵汽蚀特性有明显影响, 但这一传统方法需要较长的建模、仿真及优化周期, 无法获取全局的最优解。因此, 为了获取几何参数等与性能参数的映射关系, 提高优化效率及精度, 基于数据驱动的代理模型优化设计逐步成为了研究热点。李嘉等[15]针对复合叶轮型线复杂、难以实现快速迭代的问题, 提出了一种基于改进Bezier曲线的叶轮参数化设计方法, 为建立代理模型搭建了参数化仿真平台。除了上述代理模型优化方法之外, 科研人员亦开展了基于Kriging代理模型的离心泵优化设计研究。张宇等[16]采用了拉丁超立方抽样与Kriging代理模型结合的方式, 对某型双吸离心泵的叶轮开展了优化设计。王文杰等[17]将Kriging模型与粒子群算法结合, 对离心泵在不同设计工况下的扬程及效率进行了多目标优化。
综上, 离心泵几何参数、流动结构及性能外特性参数存在着必然联系, 建立参数间的数学映射关系、快速且智能地完成离心泵的优化设计具有极高的理论及工程意义[18–19]。而上述基于Kriging等数据驱动代理模型的相关研究均以离心泵的扬程及效率为优化目标, 尚未考虑汽蚀性能, 而这一性能更是航空燃油离心泵最为关注的。另外, 大部分研究均尝试将Kriging代理模型与多目标优化算法相结合, 未考虑模型加点策略的改进。因此, 以航空燃油离心泵汽蚀优化为目标, 在已开发的离心泵联合参数化仿真平台基础上, 提出一种基于Kriging的多阶段主动学习加点策略(下文简称多阶段加点策略), 并结合多目标粒子群算法, 实现燃油离心泵汽蚀特性的智能优化设计。研究所取得的成果可为我国燃油离心泵等旋转机械的智能化优化设计方法提供一定的理论支撑。
1.1 算法描述
基于Kriging进行建模及优化主要包含以下部分: 初始设计点采样、Kriging代理模型建模、主动学习加点及智能寻优。基于上述内容, 所提出的算法总体计算流程如下: 基于改进的拉丁超立方实验设计(LHS)对初始设计点进行采样; 利用初始设计点生成初始Kriging模型, 使用生成的Kriging模型对未知设计点进行预测; 为了提高Kriging模型预测精度, 使用多阶段加点策略进行加点, 最优加点位置的选择使用多目标粒子群算法搜索(MOPSO); 当Kriging模型达到目标精度后, 再次使用MOPSO算法, 求解最优目标设计点。具体算法步骤如下。
1) 基于改进拉丁正交的初始设计点采样。在进行基于Kriging建模及优化前, 基于LHS进行初始设计点采样[11]。LHS方法能得到较好的投影特性, 但由于该方法不考察采样的空间填充特性, 有可能产生不合理的采样点集。因此, 借助蒙特卡罗的思想, 对LHS方法进行改进。使用LHS多次随机生成设计点, 使用MinMax策略, 按照(1)式将输入参量归一化到[0, 1]区间, 将各输入参量的取值区间平均划分为m份, 对应m个水平, 在每个水平对应的取值范围中随机取值, 对不同设计参数的不同水平取值进行随机组合, 得到初始采样点集。
式中:xi为随机采样点;xmin为采样点中最小值;xmax为采样点中最大值。
从中选取最小距离最大的采样方案作为最终的初始设计点。通过这种方式将LHS和MinMax方法相结合, 得到一组兼有优秀投影特性与良好空间填充特性的初始采样点。
2) Kriging模型构建。首先, 对初始样本点进行归一化处理
式中:sj是矩阵x中第j列的设计点;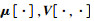 分别表示均值和协方差。
分别表示均值和协方差。
使用已知输出y(x)建立预测模型 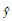 , 对于一个n维的输入 x的模型,
, 对于一个n维的输入 x的模型,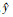 中包括回归模型F和随机过程两部分, 其表达式为
中包括回归模型F和随机过程两部分, 其表达式为
使用的回归模型是p个子函数的线性组合
式中:β: , l是回归参数;fj是第j维基函数。
随机过程z的均值为0, 其协方差满足
在zl(w)和zl(x)之间, σl2为第l维输出的方差, R(θ, w, x)为相关模型, 参数为θ。
在实际给定输出的基础上, 把回归模型的偏移量看做满足一定规律的随机过程z。输出真值可以写为
式中, α近似误差。
定义矩阵 R为随机过程z中的相关性函数, 那么Rij就表示设计点si与sj之间的相关性关系
在设计空间的不同采样点处, 随机变量之间具有一定相关性, 它们之间的协方差可表示为
式中: R (x, x ′)表示相关矩阵, 其值只与变量在空间中的距离有关; 当距离无穷大时, R = 0;当距离无穷小时, R = 1; R随距离的增大而减小。
Kriging模型采用高斯函数作为相关矩阵 R (x, x ′), 较好地评价非线性高维问题, 即
式中:m为输入变量维数;θ为待求相关参数。
采用最大似然方法进行相关参数θ的估计, 即
3) Kriging模型精度检验。随机取一组样本点评估模型的拟合程度 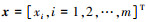 , 模型预测
, 模型预测 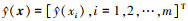 , 实测值y(x)=[y(x1), y(x2), …, y(xm)]。
, 实测值y(x)=[y(x1), y(x2), …, y(xm)]。
预测点的平均相对误差ERR计算如下
均方差ems计算如下
决定系数R2计算如下
算法仍需完成Kriging加点策略及多目标寻优等流程, 下文将重点给出提出的多阶段主动学习加点策略。
1.2 多阶段主动学习加点策略
仅使用少量初始设计点建立的Kriging模型精度较差, 需通过增加采样点提高模型精度。传统单一加点策略, 如: 均方差策略(mean square error, MSE)、改善期望策略(expected improvement, EI)和交叉验证策略(crossover, CV)等, 建立的模型精度和迭代误差下降速度有限。因此, 为了最大程度地基于较少设计点提高模型精度与迭代速度, 提出了多阶段加点策略(multi-stage adding strategy, MSAS)。鉴于篇幅, 此处不再详细介绍3个单一加点策略, 只给出多阶段加点策略的算法流程。
计算过程涉及3个阶段, 且每个阶段根据不同的判据(误差数量级下降判据、第一重收敛准则、第二重收敛准则)进行有效切换。另外, 3个阶段中, 第一阶段采用MSE加点策略, 第二阶段采用3种加点策略(CV、EI、MSE)结合的加点方式, 第三阶段采用EI加点策略。具体步骤如下:
1) 第一阶段, 使用迭代误差下降最快的MSE策略进行加点。由(12)式得到Kriging预测误差均方差, 利用其数量级对迭代误差下降速度判定是否进行下一阶段加点。该判据为:
若均方差在连续15个迭代步中下降超过0.3个数量级, 则保持使用均方差策略。即
若不满足(14)式时, 认为MSE策略已无法有效改善全局精度, 则进入第二阶段。
2) 在第二阶段, 结合CV、EI、MSE 3种加点策略进行“伪并行加点”。由于第二阶段中涉及3种加点策略, 且未同时加点, 这一阶段的切换判据较为特殊, 包括阶段内3个加点策略的切换判据与第二阶段切换至第三阶段的切换判据。
一方面, 采用(14)式所示的误差数量级下降判据作为第二阶段内各加点策略切换的判据。其中, 若不满足(14)式, 则按顺序切换至下一策略。此外, 当满足误差数量级下降判据时, 仍要根据当前加点是否过密来进行一次判定, 若产生的新点与已知点距离小于输入变量定义域宽度的1%, 则继续使用当前加点策略。若不满足, 则直接切换至MSE策略。
另一方面, 采用第一重收敛准则判定是否进入第三阶段, 该准则为:
若最大预测误差ems, max满足(15)式, 则认为全局精度已满足要求。
式中, ε1为初始点各输出参数的2%。
3) 在第三阶段, 使用EI策略进行加点。利用EI策略优先提高局部精度的特点, 以提高最优解附近精度。最终, 采用第二重收敛准则判定是否结束加点, 该准则具体为:
若最大预测误差ems, max满足(16)式, 则认为局部精度已满足要求。
式中, ε2为初始点各输出参数的1%。
通过上述步骤, 可完成多阶段加点策略, 以提高Kriging模型的求解精度及迭代速度。
2 数学算例验证
为验证多阶段加点策略的有效性, 以一维函数、多维函数等测试函数作为数学验证算例, 与单一加点策略进行对比分析。
2.1 一维函数
(17) 式所示函数为一维多峰函数MP, 分别对比不同单一加点策略在该函数下的加点迭代结果预测的MSE、EI及CV值。同时, 对多阶段加点策略在第一阶段结束时、第二阶段结束时和第三阶段结束时的迭代结果进行分析。
MSE策略能精确反映迭代误差数量级, 但在数值上有一定差异。EI策略会优先提高最优点附近采样点密度, 但其全局最优值远大于局部最优值。CV策略只需计算当前点的CV值, 不需要使用优化算法寻优, 计算量小。另外, 对于MP问题, MSE策略、EI策略和CV策略需分别使用25个点、35个点和33个点达到全局精度10-4。
通过优化算法寻找最优位置, 可以发现EI值多峰特征较弱, 且EI指标随着精度的提高, 数量级不断下降。CV指标峰特征最为明显, 且随着模型精度的提高, 数量级不断下降。
第一阶段结束后Kriging模型整体误差已经较小。第二阶段结束后模型拟合值与真实值拟合程度较高。在第三阶段, 最优值附近仅添加2个点, 使全局精度达到10-5, 第三阶段结束后全局精度达到10-4。总的来看, 单一加点和多阶段加点均能达到全局精度, 但多阶段加点策略的加点次数最少。
2.2 多维函数
分别以多输入单输出的曲面函数SC、PK及SE,多输入多输出函数BR3为测试算例进行单一加点策略与多阶段加点策略的对比验证。
(18)~(20)式分别为SC、PK及SE函数, (21)式为BR3函数。
通过分析可以看出, 3种单一加点策略中, MSE策略具有最快的误差下降速度, 能够比较准确地定位误差最大位置; EI策略误差下降速度最慢, 达到相同精度需要更多的点, 但其会优先保证最优点附近精度, 同时兼顾全局精度; CV策略误差下降速度稍慢, 但其可以反映出真实的误差特点, 作为MSE的补充。
另外, 通过多阶段加点策略与单一加点策略的对比发现: 多阶段加点策略达到相同精度所需要的时间优于其他3种策略; 与单一MSE策略相比, 其结果具有更高的最优解局部精度, 这种特性将提高全局最优位置的准确性, 使优化结果更为有效。总之, 对不同问题各方法的表现不尽相同, 在提高全局精度方面, 各算法从优到劣排序为MSE>MSAS>CV>EI; 在提高迭代速度方面, MSAS>MSE>CV>EI。
为了更好地反映所提出的多阶段加点策略的迭代效果, 在相同测试数学函数上提高收敛标准, 对迭代结果进行分析。此外, 在提高收敛标准后, 所提出的基于Kriging多阶段主动学习加点策略快速、精确地实现了一维、多维等数学算例的拟合, 表明该方法行之有效。
3 燃油离心泵汽蚀优化算例验证
3.1 某型燃油离心泵算例
以某型航空燃油离心泵为对象, 利用所提出的基于Kriging多阶段主动学习加点策略, 对该型离心泵汽蚀特性开展优化设计, 并通过CFD完成优化前后离心泵汽蚀仿真分析及对比。该型离心泵的相关性能参数为: 流量8.23 kg/s,进口压力0.8 MPa,扬程1 509 m,驱动功率245 kW。
3.2 离心泵汽蚀优化方案
3.2.1 优化变量
为了更好地反映离心泵汽蚀特性, 优化目标选为: 汽蚀系数Kd、泵汽蚀余量RNPSHr和汽蚀比转数Nss。其中, 汽蚀系数Kd反映流场中压降与动压头的相对关系, 表征通过流道时流体动量损失的相对大小, 其值越大反映泵汽蚀特性越好。泵汽蚀余量RNPSHr主要与泵吸水室形状、进口几何尺寸有关, 对于泵的设计与使用十分重要, 在不小于临界汽蚀余量的前提下, 其值越小泵的汽蚀特性越好。汽蚀比转数Nss反映泵抗汽蚀性能的好坏, 其值越大泵的汽蚀特性越好。3个参数分别根据(22)~(24)式预测。
式中: Kd为汽蚀系数; p为局部压力, Pa; pv为汽化压力, Pa; ρ为流质密度, kg/m3; v0为叶轮进口稍前处流速, m/s。
式中: v0为叶轮进口稍前处绝对流速, m/s; w0为叶轮进口稍前处相对流速, m/s; λ为叶片进口压降系数。
式中, Q为体积流量, m3/s。
对于原型泵, 设计工况下汽蚀特性参数分别为:
·汽蚀系数Kd=9.990 2
·泵汽蚀余量RNPSHr=53.556
·汽蚀比转数Nss=8 038.3
另一方面, 根据离心泵设计过程中几何参数对性能的敏感度[15, 17], 优化的输入参数选择离心泵叶轮的主要外形几何参数与叶片几何参数, 包括吸入直径ds、叶轮直径d2、出口宽度b2、包角φ和叶片出口安放角β2。
3.2.2 汽蚀整体优化方法
通过上述分析, 确定离心泵的汽蚀优化问题可表示为
图 1为离心泵汽蚀特性优化整体方案。其中, 优化过程基于所开发的离心泵联合参数化仿真平台。通过Python外部批处理的方法完成几何参数新加点的建模、网格划分及汽蚀仿真, 使整个优化过程自动化执行, 以提高数值仿真过程的连续性、降低工作量、提高优化效率。使用改进的拉丁超立方实验设计进行采样, 初始设计点采样个数为15。Kriging模型求解过程的收敛条件分别选择初始优化目标参数的10%和2%。使用MOPSO算法完成多目标寻优。加点策略使用所提出的MSAS策略。
另外, 设计点和新加点的输出参数由CFD仿真计算得到, 使用AMD 7H12 @ 2.60 GHz的128核并行计算队列。边界条件为: 进口压力0.8 MPa、出口流量8.2 kg/s。求解模型采用k-ε模型与完全汽蚀模型, 收敛判据为残差小于10-4。为了求解均匀性及有效性, 每次计算的最大迭代次数均为150。
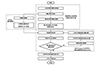 |
图1 离心泵汽蚀特性优化整体方案 |
4 优化结果与分析
4.1 代理模型求解结果
在迭代加点至223步后, Kriging模型达到了预定的收敛条件, 总耗时约1 784 min。在多阶段加点过程中, 加点迭代63步后, 第一阶段加点过程结束; 加点迭代79步后, 第二阶段加点过程结束; 加点迭代223步后, 第三阶段加点过程结束, Kriging最大预测误差下降到收敛误差以内, 优化过程结束。
分别分析3个阶段内预测误差均方差与加点个数的关系, 发现第一阶段预测误差的下降速度最快, 这是由于该阶段使用的MSE加点策略直接从ems, max处加点。第二阶段初期最大预测误差迅速上升。由于该阶段中3种加点策略不断切换, 更多局部特征被不断发现、加入, 出现波动、整体趋势下降的现象。第三阶段预测误差下降缓慢, 出现局部上升的现象, 这是由于该阶段所采用的EI加点策略对局部最优点更为敏感, 导致其加点位置与已知点更为接近。
通过所提出的优化方法, 对离心泵的汽蚀特性进行优化, 表 1为优化前后离心泵几何参数的对比结果。基于优化结果对原型泵与优化泵进行三维建模, 如图 2所示。
可见, 优化后叶片进口宽度明显增大, 进口处腔室体积增大, 进口过流面积增大, 使得液流在进口处的扩散作用减缓, 以降低进口处的压力损失。叶轮出口宽度没有明显变化, 该参数对汽蚀特性的影响并不明显。此外, 叶轮主叶片前缘宽度加厚, 分流叶片前缘前移, 叶片包角增大、总长度增加, 减小了液流在叶片前缘处的液压冲击与回流, 降低了叶片前缘处的局部压力损失, 有助于抑制空化现象, 提高汽蚀特性。
输入参数取值范围与设计初值
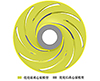 |
图2 优化前后离心泵叶轮三维模型结果 |
4.2 基于CFD的汽蚀特性验证结果
4.2.1 网格模型
叶轮做为主要供能部件, 流动规律复杂, 基于AutoGrid划分为六面体结构化网格; 蜗壳对离心泵仿真精度影响较小, 基于ICEM划分为四面体非结构化网格。最终, 叶轮网格总数为902 656, 蜗壳网格总数为465 464, 进口装置网格总数为39 000。
4.2.2 汽蚀特性预测结果对比
基于汽蚀仿真结果, 根据(22)~(24)式对优化前后离心泵的汽蚀特性进行预测。
首先, 根据优化泵的汽蚀仿真结果, 对比验证多阶段加点策略的有效性, 结果见表 2。可以看出, 所提出的多阶段主动学习加点策略预测结果与汽蚀仿真结果最大误差为3.49%, 该方法能够精确地实现汽蚀特性的预测。
其次, 对比优化前后离心泵的汽蚀仿真结果, 验证所提出的方法在离心泵汽蚀特性优化应用上的有效性。表 3为优化前后离心泵汽蚀特性对比结果。可看出优化泵各个汽蚀特性参数均有明显提升, 其中, 汽蚀系数提高30.83%, 泵汽蚀余量下降9.14%(仍大于临界汽蚀余量), 汽蚀比转数下降7.17%, 泵内因空化产生的气体含量下降17.27%, 明显地提升了原型泵的汽蚀特性。此外, 优化泵的扬程提高7.5%, 效率略有上升, 保证汽蚀特性优化同时, 兼顾了泵的增压能力。
优化泵汽蚀仿真结果与多阶段加点策略预测结果对比
优化前后离心泵汽蚀特性对比
4.2.3 流场分布结果对比
为了更详细地对比优化前后离心泵性能变化, 分别对原型泵、优化泵的气液两相分布、压力分布和相对速度分布结果进行对比分析, 图 3为设计工况下离心泵中间轴向截面上的仿真结果对比。
可以看出: 原型泵与优化泵的气液两相分布整体趋势基本一致, 在叶轮叶尖处均产生了一定的空泡区域, 但优化泵的空泡分布区域更小。另外, 原型泵进口附近产生了明显的旋涡流动, 部分主叶片压力侧产生了细长的二次分离流结构。蜗壳中近壁面区域的流速较快, 出口处形成了一定的旋涡流动, 造成了局部压力能的严重损失; 优化泵进口处的回流现象减弱, 叶轮中流体速度有一定程度提高。蜗壳扩散管中的涡结构稍微减弱, 出口处的压力能损失大幅减小, 流动更加平缓。
综上所述, 与原型泵相比, 优化泵具有更平稳的流动特征、更高的增压能力与更低的进口压力损失, 与优化泵更优的汽蚀特性一致。因此, 可以验证所提出的基于Kriging多阶段主动学习加点策略能够有效地实现离心泵的汽蚀特性优化。
 |
图3 设计工况下离心泵中间轴向截面仿真结果 |
5 结论
提出了一种基于Kriging的多阶段主动学习加点策略, 并将该方法在数学算例、航空发动机燃油离心泵的汽蚀特性上进行了应用。主要结论如下:
1) 通过与3种单一加点策略(MSE加点策略、EI加点策略、CV加点策略)方法对比, 验证了所提出的多阶段加点策略在常规数学算例的有效性; 此外, 针对某型航空燃油离心泵的汽蚀特性应用算例, 在设计工况下优化泵汽蚀仿真结果与基于Kriging的多阶段加点策略预测结果最大误差为3.49%, 结果高度一致, 进一步验证了该方法的有效性;
2) 对比了优化泵和原型泵的汽蚀特性预测结果, 发现在设计工况下优化泵汽蚀系数、泵汽蚀余量、汽蚀比转速以及气体含量占比等参数均优于原型泵。同时, 优化泵的扬程和效率亦优于原型泵;
3) 对比优化泵和原型泵的流场分布结果, 发现相比于原型泵, 优化泵的内部流动更为均匀, 不利流动(叶尖空泡分布、叶片进口漩涡、叶片压力侧分离流、蜗壳出口旋涡等)得到了一定的改善, 保证了优化泵汽蚀特性、增压能力及效率提高。
本文提出的方法虽然针对某型航空燃油离心泵, 但也可以推广至各类离心式旋转机械的优化设计中, 具有一定的通用性。
致谢
感谢航空发动机及燃气轮机基础科学中心项目(P2022-A-V-001-001)的资助。
References
- LIU Shangqin. Investigation of centrifugal pump used as aeroengine main fuel pump[J]. Aeroengine, 2006, 32(2): 43–45 [Article] (in Chinese) [Google Scholar]
- FAN Siqi. Aeroengine control[M]. Xi'an: Northwestern Polytechnical University Press, 2008, 24–27 (in Chinese) [Google Scholar]
- XIAO Hongling, LI Huacong, LI Jia, et al. Modeling method of variable cycle engine based on QPSO hybrid algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 305–315 [Article] (in Chinese) [Google Scholar]
- LI Jia, LI Huacong, ZHANG Wei, et al. Transient flow structures and pressure pulsations of a high-pressure aero-fuel cen-trifugal pump[J]. Journal of Northwestern Polytechnical University, 2022, 40(1): 199–205 [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
- LI Jia, LI Huacong, WANG Shuhong, et al. The profile optimization study of muti-diversion combination inducer and impeller[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 6(5): 953–960 (in Chinese) [Google Scholar]
- YANG Junhu, BIAN Zhong, ZHONG Chunlin, et al. Method for selecting centrifugal pump impeller outlet angle based on calculation of centrifugal pump impeller's hydraulic loss[J]. Journal of Xihua University, 2016, 35(3): 89–112 (in Chinese) [Google Scholar]
- WAN Lijia, SONG Wenwu, LI Jinqiong. Effect of blade packet angle on unsteady flow of solid-liquid two-phase of centrifugal pump with low ratio speed[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(7): 37–44 [Article] (in Chinese) [Google Scholar]
- YUAN Jianping, WANG Zhenqing, FU Yanxia, et al. Experiments on the backflow characteristics at the inlet of a moderate-speed centrifugal pump[J]. Journal of Vibration and Shock, 2020, 39(22): 8–15 [Article] (in Chinese) [Google Scholar]
- ZHAO A, WU P, WU D Z, et al. The optimization of a low specific speed pipeline pump[C]//Proceedings of the 6th International Conference on Pumps and Fans with Compressors and Wine Turbines, Beijing, 2013 [Google Scholar]
- HAN X D, KANG Y, SHENG J P, et al. Centrifugal pump impeller and volute shape optimization via combined NUMECA, genetic algorithm, and back propagation neural network[J]. Structural and Multidisciplinary Optimization, 2020, 61: 381–409 [Article] [CrossRef] [Google Scholar]
- LIU Xianwei, LI Huacong, SHI Xinxing,et al. Optimization design of composite impeller of aero-centrifugal pump based on particle swarm optimization[J]. Journal of Propulsion Technology, 2019, 40(8): 1743–1751 [Article] (in Chinese) [Google Scholar]
- LUO Yunxia. Study on the influence of the leading edge slotted blade on the cavitation performance of centrifugal pump[D]. Lanzhou: Lanzhou University of Technology, 2022: 13–35 (in Chinese) [Google Scholar]
- ZHAO Weiguo, ZHOU Zhongliang, LUO Yunxia, et al. Research on cavitation suppression effect of tiny blade in the shroud of centrifugal pump[J]. Journal of Engineering Thermophysics, 2022, 43(11): 2926–2936 [Article] (in Chinese) [Google Scholar]
- CHEN Bing, LI Zhipeng, LUO Youru, et al. Cavitation performance optimization of centrifugal pump based on CFD technology[J]. Journal of Engineering Thermophysics, 2022, 43(4): 21–25 [Article] (in Chinese) [Google Scholar]
- LI Jia, HAN Xiaobao, LI Huacong, et al. Parametric design and simulation for an aero-fuel centrifugal pump with compound impeller based on improved bezier-curve[J]. Journal of Propulsion Technology, 2022, 43(7): 201009 [Article] (in Chinese) [Google Scholar]
- ZHANG Yu, TAN Gang, ZHANG Yunqing, et al. Kriging based multi-objective optimization for hydraulic performance of centrifugal pump[J]. Journal of Huazhong University of Science and Technology, 2015, 43(4): 54–57 [Article] (in Chinese) [Google Scholar]
- WANG Wenjie, DENG Qifan, PEI Ji, et al. Application of particle swarm optimization to improve the performance of a centrifugal pump with vaned diffuser[J]. Journal of Northeast Electric Power University, 2021, 41(4): 73–79 [Article] (in Chinese) [Google Scholar]
- SAFIKHANI H, KHALKHALI A, FARAJPOOR M. Pareto based multi-objective optimization of centrifugal pumps using CFD, neural networks and genetic algorithms[J]. Engineering Applications of Computational Fluid Mechanics, 2011, 5(1): 37–48 [Article] [CrossRef] [Google Scholar]
- JIANG Bingxiao, YANG Junhu, WANG Xiaohui, et al. Optimization of twisted blade of centrifugal pump based on high dimensional machine learning method[J]. Journal of Aerospace Power, 2022, 37(3): 629–638 [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 离心泵汽蚀特性优化整体方案 |
| In the text | |
 |
图2 优化前后离心泵叶轮三维模型结果 |
| In the text | |
 |
图3 设计工况下离心泵中间轴向截面仿真结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


