| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 656 - 663 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740656 | |
| Published online | 23 September 2019 | |
Adaptive Wing Morphing Strategy and Flight Control Method of a Morphing Aircraft Based on Reinforcement Learning
基于增强学习的变体飞行器自适应变体策略与飞行控制方法研究
1
School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China
2
Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109, China
Received:
8
August
2018
The morphing aircraft can change different wing shapes or geometries to achieve the optimal flight performance according to various mission scenarios. In this paper, DATCOM is used to calculate aerodynamic parameters based on Firebee UAV morphing aircraft with different wing configurations and analyze aerodynamic characteristics. A novel adaptive wing morphing strategy for morphing aircraft based on reinforcement learning method is proposed. This method can highly meet the demand of keeping optimal performance in multiple flight conditions, and the adaptive wing morphing strategy, three-loop normal load altitude controller and sliding mode velocity controller can together make sure stability of morphing aircraft during morphing process with good tracking performance.
摘要
变体飞行器能根据飞行环境和飞行任务的需要,相应地改变外形,从而始终保持最优的飞行状态,以满足在大飞行包线下执行多种任务的要求。以具有多种翼型的Firebee无人机作为研究对象,利用DATCOM计算气动数据,并展开气动分析。之后,基于增强学习理论,提出一种新型的变体飞行器翼型自适应控制方法。该方法可以很好地满足变体飞行器在多任务状态下保持最优性能的需要,并且设计的高度子系统的三回路法向过载控制器和速度子系统的滑模控制器可以确保飞行器在变体过程中保持稳定,并且跟踪误差较小。
Key words: morphing aircraft / longitudinal model / reinforcement learning / flight control
关键字 : 变体飞行器 / 纵向模型 / 增强学习 / 飞行控制
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
传统飞行器只针对特定的飞行条件展开设计, 其飞行性能会在非主要飞行条件下存在妥协。而变体飞行器可以根据不同的飞行场景(如:起飞、侦查、攻击、着陆等), 改变不同的翼型、机翼剖面等参数[1]。在过去20年中, 变体飞行器有以下研究的热点问题:飞行动力学、控制理论、结构和材料。这些技术使得飞行器可以在不同的飞行条件下飞行并且会更加高效。对变体技术的研究可以划分为2个领域:对于变体机构、材料和机翼的研究以及对于变体飞行器飞行动力学和控制问题的研究。
Grant等设计了一种多关节变后掠的飞行器[2], 该飞行器翼面内侧和外侧都可以独立变形, 该文章分析飞行力学并且研究了机翼变形所带来的效果, 并提出在不同变体轨迹下的时变特征方程。
在DARPA MAS项目中, 洛马公司设计了一个Z型机翼的变体无人机。乐挺等针对该构型, 提出纵向线性变参(LPV)模型[3], 将气动力和气动力矩通过折叠翼的角度进行表示。在机翼折叠过程中, 开环系统的时间响应表明纵向线性变参(LPV)模型可以很好地匹配纵向非线性模型响应情况。童磊利用凯恩方法, 提出非对称变体飞行器的多刚体动力学模型[4]。该模型可以详细表征无人机在变体过程中的动力学以及响应过程, 并且使用非对称变体进行滚转控制。Liu针对新型控制执行器(ICE)飞行器, 提出一种鲁棒控制方法[5]。Valasek提出一种基于增强学习的变体飞行器变体策略[6], 并利用结构化自适应模型逆控制器(SAMI)控制变体飞行器跟踪参考轨迹。但该方法只是以一个椭球体作为变体飞行器, 只具有理论意义。
针对变体飞行器的纵向运动的控制问题, 本文首先建立变体飞行器的纵向动力学方程, 之后给出气动系数。变体飞行器飞行控制器中的高度控制采用三自由度法向过载自动驾驶仪, 速度控制采用滑模控制方法; 而在外环的翼型控制上, 提出一种基于增强学习的变体飞行器翼型自适应控制方法。本方法可以使得变体飞行器根据飞行条件和任务剖面自主选择外形, 从而获得最优气动性能。
1 变体飞行器建模
气动外形大尺度变化的飞行器, 在变形过程中, 飞行器的气动力, 质心等参数都将发生大幅度变化, 表现出了大时变、强非线性等特点。传统的单刚体飞行器建模方法不再能够精准地反映变体飞行器的动力学特性, 必须采用多刚体建模方法。
1.1 纵向动力学方程
变后掠飞行器是个复杂多变的动力学系统, 与常规飞机不同, 它在飞行过程中可以改变自身机翼结构, 改变气动特性, 使得飞行器的动力学和运动学模型随之变化。本节将基于牛顿-欧拉公式对变体飞行器建立多刚体动力学模型, 随后依据该模型进行变体飞行器的动态响应分析。该方法最早由杨贯通在文献[7]中提出, 本文在此基础上, 重新给出附加力和附加力矩的表示形式。为了既不失准确性又简化模型, 在模型建立之前必须对相应的因素进行处理, 提出如下假设:
1) 变体飞行器的机体、后掠翼等部件的质量和密度均不发生变化。
2) 变后掠飞行器质量分布均匀, 几何外形关于机体纵向平面对称, 并且两侧机翼同步变形。
在地面坐标系中, 变体飞行器每个刚体的质心运动方程为
式中,mi为第i个刚体的质量, Vi为第i个刚体质心的运动速度矢量, Fi为作用在第i个刚体质心的合外力矢量。
为了便于进行推导和描述, 进行如下定义:
1) 定义地面坐标系到机体系原点的矢径为ro。
2) 定义点Oi为第i个可活动机翼的质心。
3) 定义机体坐标系原点Ob到点Oi的矢径为Si。详见图 1。
4) 定义地面坐标系原点A到点Oi的矢径为rgi。
5) 定义下标0表示机身, 下标1表示左后掠翼, 下标2表示右后掠翼。
机体坐标系采用美式坐标系, X轴指向前, Y轴指向右, Z轴指向下。选取机身部分的质心作为机体系的原点, 从而使得机体坐标系在变体过程中保持固定。定义VSi如下
对变体飞行器机体、左翼和右翼3个部分的质心运动方程相加, 并抵消内力后, 得到下式
Faero表示气动力, G表示重力, T表示推力, 这3个力与传统的单刚体动力学模型相同。使用Fs表示附加力
假设后掠翼质心在机体坐标系Obxbzb平面内并且只考虑纵向运动, 可以得到
利用(4)式和(2)式, Fs可以化简为
对于每个机翼, 绕Ob点的绝对动量矩为
式中,Si*表示每个质点元相对于Ob的矢径, Vi*表示每个质点元在惯性系下的速度。
对变体飞行器机体、左翼和右翼3个部分的绕质心转动方程相加, 得到
Maero表示气动力矩, 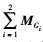 表示左翼和右翼对Ob的重力力矩之和。(7)式中等式左边第三项可以化简为
表示左翼和右翼对Ob的重力力矩之和。(7)式中等式左边第三项可以化简为
最终可以得到变后掠飞行器纵向动力学方程
式中, 变形引起的干扰力和干扰力矩可以表示为
推力模型如下
式中,ρ是密度, V是速度, CT是动力系数, CT作为控制参数。
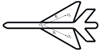 |
图1 S1和S2矢量 |
1.2 气动数据获取及分析
选取Teledyne Ryan BQM-34 “Firebee”作为基准飞行器, 该飞行器最快可以飞行0.97马赫, 高达18 000 m。Joshi等人基于此飞行器, 针对不同飞行条件, 优化得出不同的翼型[8]。Seighler将Firebee的不同翼型划分为4个任务:巡航、起飞、机动和俯冲[9]。本文选取俯冲(后掠角60°)和巡航(后掠角15.97°)这2个翼型作为基准。除此之外, 在这2个翼型中间选择4个后掠角(25°, 35°, 45°, 55°), 利用后掠角插值计算得出不同后掠角对应的展长和弦长, 总计得到6个翼型尺寸, 详见图 2。本文仅以后掠角的数值代指相应的翼型。另外, 由于飞行器在后掠角55°和60°构型下的气动参数非常接近, 在下述分析时未表示55°后掠角下的气动参数。
变体飞行器的气动参数不但受速度和高度的影响, 还随着机翼的后掠而变化, 本文采用DATCOM计算相应后掠角下的气动数据。2种基准翼型的几何参数见表 1。
机身质量和惯量相关参数见表 2。
为了便于气动特性分析, 采用准定常假设:变体飞机所受气动力和对应的气动参数、气动导数仅与当前飞机的构型以及飞行状态有关, 与变形前后的状态无关。
在高度9 144 m, 马赫数0.5的条件下利用DATCOM计算出不同飞行状态下变体飞行器的气动参数。λ表示后掠角。
从图 3可以看出, 随着后掠角的增大, 升力系数和阻力系数都在逐渐减小, 升力系数与攻角近似呈一次线性关系, 阻力系数与攻角近似呈二次曲线关系。
从图 4可以看出, 升阻比随着后掠角的增大而减小。当攻角小于6°时, 攻角越大升阻比越大, 攻角大于6°之后, 攻角越大升阻比越小。
从图 5可以看出, 在一定范围内, 随着后掠角的增大, 升力系数的减小幅度大于压心位置的后移幅度, 从而导致俯仰力矩系数的绝对值减小。
从图 6可以看出, 稳定度随后掠角的增大而增大。俯冲翼型的稳定度在-0.56左右, 巡航翼型的稳定度在-0.33左右。大后掠时, 压心后移, 稳定度增加。
从图 7可以看出, 操稳比随后掠角的增大而减小。俯冲翼型的操稳比在0.4左右, 巡航翼型的操稳比在1.3左右。
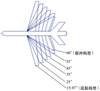 |
图2 6种翼型的俯视图 |
2种基准翼型的几何参数
质量惯量参数
 |
图3 不同后掠角下升力系数和阻力系数随攻角变化曲线 |
 |
图4 不同后掠角下升阻比变化曲线 |
 |
图5 不同后掠角下俯仰力矩系数随攻角变化曲线 |
 |
图6 稳定度Cmα/CLα曲线 |
 |
图7 操稳比Cmδe/Cmα曲线 |
2 基于增强学习的翼型自适应控制
前文中已经给出纵向动力学方程和气动参数。以此为基础, 本节重点研究翼型的自适应控制方法。对于给定任务剖面(给定期望的速度和高度)的每个飞行状态(如:巡航、爬升和俯冲等), 通过多次迭代的Q学习方法找出当前状态下的最优行动值, 即选择相应的最优后掠角。
2.1 Q学习的算法步骤
强化学习又称再励学习, 是指从环境状态映射到行为动作的学习, 以使动作从环境中获得的奖励值最大。强化学习强调在与环境的交互中学习, 学习系统不需要获得各种状态下的期望输出信号, 而仅根据从环境中获得的评价性反馈信号(增强信号)来实现学习目标。这种评价性反馈信号在实际中往往易于获得, 因此强化学习能够在不确定和复杂环境中得以应用。而Q学习方法是强化学习中很重要的方法之一[10]。
首先, 以任意数值初始化Q(s, a);其次, 在每个仿真场景内计算:
1) 采用策略选择机制, 根据当前的Q(s, a)选择需要执行的动作a。
2) 执行动作a, 观察奖励R与下一个状态s′。
3) 更新
迭代, 直到计算完毕全部仿真场景。
2.2 Q学习的算法设计
变体飞行器的典型飞行阶段共3个:爬升、巡航和俯冲3种。在给定期望高度和速度的前提下, 对于爬升阶段, 期望获得最小的阻力D以节省燃料。对于巡航阶段, 期望获得最大的升阻比L/D。对于俯冲阶段, 期望获得最小的阻力D。通过Q学习, 在不同的飞行阶段选择后掠角, 从而使得3个阶段的目标函数值最大。
Q学习算法中的状态集S, 对于爬升阶段, 状态集包含阻力这一个维度; 对于巡航阶段, 状态集包含升阻比这一个维度; 对于俯冲阶段, 状态集包含阻力这一个维度。
2.2.1 状态空间与行动空间设计
本文的期望高度轨迹分为3个阶段:俯冲、巡航和爬升。这3个阶段作为状态量, 对应的序号分别为{1, 2, 3}。后掠角的数值作为行动集A的参数, 共包含{15.97°, 25°, 35°, 45°, 55°, 60°}这6种构型, 对应的序号依次为{1, 2, 3, 4, 5, 6}。故S的状态空间为{1, 2, 3}, A的行动空间为{1, 2, 3, 4, 5, 6}, Q(S, A)的维数为二维, Q(S, A)的初始值为任意值。对于每个阶段, 需要找到最优的后掠角, 使得变体飞行器具有最优的性能。
2.2.2 奖赏函数与策略选择机制设计
在巡航阶段, 需要获得最大升阻比。故奖赏函数设计为R2=CL/CD。
在俯冲和爬升阶段, 由于期望的高度和速度已经给定, 需要获得最小的阻力。故奖赏函数设计为R1, 3=1/CD。
采用ε贪婪策略, 即ε为一个很小的概率值, 以ε的概率选择能使当前状态的Q(S, A)最大的行动集中的值, 以(1-ε)的概率选择行动集中的随机值。
2.3 最优翼型变形策略
设定最大迭代次数为100次, 由于该场景下的Q函数和奖赏函数均与飞行状态无关, 而只与飞行器构型有关。所以先离线学习, 得出不同飞行阶段的最优翼型, 再应用到含有飞行控制器的纵向运动仿真中。如果Q函数和奖赏函数中含有飞行状态相关变量, 可以在线进行训练和学习, 通过多次飞行仿真获得最优的翼型变形策略。
图 8和图 9表明, 在俯冲和爬升阶段, 最优翼型为60°后掠角; 图 10表明, 在巡航阶段, 最优翼型为15.97°后掠角。
 |
图8 迭代次数与最优行动集序号(俯冲) |
 |
图9 迭代次数与最优行动集序号(爬升) |
 |
图10 迭代次数与最优行动集序号(巡航) |
3 飞行控制与纵向动力学仿真
3.1 控制器及任务剖面设计
高度控制器采用经典的三回路法向过载自动驾驶仪, 速度控制采用滑模控制器。由于高度控制器采用的是经典控制方法, 本文不再展开阐述。重点对速度控制的滑模控制器进行说明。
攻角较小时, 可以忽略公式(9)中的Fszsinα。对公式(9)做输入输出线性化, 得到速度控制子系统的结构如下
令σV=V-Vc作为跟踪误差和滑模面, 可得
式中,k′V=0.15, ε′V=0.05, ΔV=0.6。
根据2.3节优化结果, 巡航时采用15.97°后掠角, 俯冲和爬升时采用60°后掠角。期望的高度和后掠角变化指令见图 11。变形策略的采用可以很好地减少所需推力, 进而减少燃料消耗。
 |
图11 期望高度和后掠角变化指令 |
3.2 纵向运动仿真
初始角速度为0°/s, 弹道倾角为0°, 俯仰角为3.7°, 初始高度9 135 m, 初始速度152 m/s, 初始翼型为15.97°后掠角。
从高度跟踪(见图 12)和速度跟踪曲线(见图 13)可以看出, 在变形的过程中, 高度跟踪误差较小, 在-0.35~0.05 m之间。速度跟踪误差在0.02 m/s之内。
从姿态角曲线(见图 14)可以看出, 在每个变形过程的起始阶段, 攻角会有跳变, 但幅度不大。而弹道倾角变化平缓。在9 135 m高度和15.97°后掠角下, 平衡攻角为3.67°, 在8135米高度和15.97°后掠角下, 平衡攻角为3.22°。在60°后掠角的俯冲和爬升阶段, 升阻比较小, 所需要的攻角较大, 在5°以上。
从姿态角曲线速度(见图 15)可以看出, 在每个变形过程的起始阶段, 姿态角速度会有跳变, 但幅度不大。姿态角速度为-0.6°~0.6°。
轴向干扰力(见图 16)在-10~7 N之间。法向干扰力在-20~20 N之间。
变形引起干扰力矩包括MSG和MSD。从图中可看出, MSD在±100 Nm之间, MSG在400~1 800 Nm之间。在爬升和俯冲阶段, 俯仰角速度会变化, 从而导致MSD发生相应变化。而干扰力矩MSG是由机翼的质心变化引起, 与MSD相比较大, 需要在控制器设计时进行考虑。
从推力系数和俯仰舵偏角曲线(见图 18)可以看出, 在变形的过程中, 推力系数先减小后增大, 但变化幅度不大, 这是因为变形过程会有干扰力, 同时升阻特性也会改变。在变形过程中, 俯仰舵偏角也会根据升阻特性发生相应的变化。
 |
图12 高度跟踪曲线 |
 |
图13 速度跟踪曲线 |
 |
图14 姿态角曲线 |
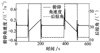 |
图15 姿态角速度曲线 |
 |
图16 干扰力 |
 |
图17 干扰力矩 |
 |
图18 推力系数和俯仰舵偏角 |
4 结论
本文基于Firebee的巡航和俯冲2种构型参数, 计算得出共6种构型的气动数据和几何尺寸。并且, 提出改进的变体飞行器纵向动力学方程, 该模型充分描述变体过程中的质量分布以及惯量变化。与传统的单刚体飞行器纵向模型相比, 该模型会有变体带来的附加力和附加力矩。在此基础上, 本文应用增强学习的方式, 使得变体飞行器在变体过程中根据飞行条件自主选择最优的构型。仿真结果表明, 本文提出的基于增强学习的变体飞行器自适应变体策略和飞行控制器具有很好的飞行性能, 同时可以保持变体过程中的飞行稳定。
References
- Barbarino S, Bilgen O, Ajaj R M, et al. A Review of Morphing Aircraft[J]. Journal of Intelligent Material Systems & Structures, 2011, 22(9): 823–877 [Article] [CrossRef] [Google Scholar]
- Grant D, Abdulrahim M, Lind R. Flight Dynamics of a Morphing Aircraft Utilizing Independent Multiple-Joint Wing Sweep[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2006 10.1260/1756-8293.2.2.91 [Google Scholar]
- Yue T, Wang L, Ai J. Longitudinal Linear Parameter Varying Modeling and Simulation of Morphing Aircraft[J]. Journal of aircraft, 2013, 50(6): 1673–1681 [Article] [CrossRef] [Google Scholar]
- Tong L L, Ji H. Multi-Body Dynamic Modelling and Flight Control for an Asymmetric Variable Sweep Morphing UAV[J]. The Aeronautical Journal, 2014, 118(1204): 683–706 [Article] [CrossRef] [Google Scholar]
- Liu C, Zhang S. Novel Robust Control Framework for Morphing Aircraft[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 281–287 [Article] [CrossRef] [Google Scholar]
- Valasek J, Doebbler J, Tandale M D, et al. Improved Adaptive-Reinforcement Learning Control for Morphing Unmanned Air Vehicles[J]. IEEE Trans on Systems Man & Cybernetics Part B, 2008, 38(4): 1014–1020 [Article] [CrossRef] [Google Scholar]
- Yang Guantong. Research on Modeling and Control of Morphing Flight Vehicles[D]. Beijing, Beijing Institute of Technology, 2015 (in Chinese) [Google Scholar]
- Joshi S, Tidwell Z, Crossley W, et al. Comparison of Morphing Wing Stategies Based upon Aircraft Performance Impacts[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, 2004 https://arc.aiaa.org/doi/abs/10.2514/6.2004-1722/ [Google Scholar]
- Seigler T M. Dynamics and Control of Morphing Aircraft[D]. Virginia, Virginia Polytechnic Institute and State University, 2005 [Google Scholar]
- Wu Hongyan. The Research on Autonomous Mobile Robot Navigation Based on Reinforcement Learning[D]. Jilin, Northeast Normal University, 2009: 11–13 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 S1和S2矢量 |
| In the text | |
 |
图2 6种翼型的俯视图 |
| In the text | |
 |
图3 不同后掠角下升力系数和阻力系数随攻角变化曲线 |
| In the text | |
 |
图4 不同后掠角下升阻比变化曲线 |
| In the text | |
 |
图5 不同后掠角下俯仰力矩系数随攻角变化曲线 |
| In the text | |
 |
图6 稳定度Cmα/CLα曲线 |
| In the text | |
 |
图7 操稳比Cmδe/Cmα曲线 |
| In the text | |
 |
图8 迭代次数与最优行动集序号(俯冲) |
| In the text | |
 |
图9 迭代次数与最优行动集序号(爬升) |
| In the text | |
 |
图10 迭代次数与最优行动集序号(巡航) |
| In the text | |
 |
图11 期望高度和后掠角变化指令 |
| In the text | |
 |
图12 高度跟踪曲线 |
| In the text | |
 |
图13 速度跟踪曲线 |
| In the text | |
 |
图14 姿态角曲线 |
| In the text | |
 |
图15 姿态角速度曲线 |
| In the text | |
 |
图16 干扰力 |
| In the text | |
 |
图17 干扰力矩 |
| In the text | |
 |
图18 推力系数和俯仰舵偏角 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


