Submit your paper
Search
Menu
All issues Volume 38 / No 3 (June 2020) JNWPU, 38 3 (2020) 540-549 Full HTML
Open Access
Issue
JNWPU
Volume 38, Number 3, June 2020
Page(s) 540 - 549
DOI https://doi.org/10.1051/jnwpu/20203830540
Published online 06 August 2020

© 2019 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative Commons
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

变体飞机能改变其气动外形, 使其在执行不同飞行任务时都能保证飞行性能最优[1]。由于变体飞机优良的飞行性能和适应能力, 吸引了越来越多的学者对其进行研究。对于机翼变化的变体飞机, 机翼的过渡过程十分复杂而且重要。此类变体飞机在变形过程中, 由于质量分布、气动力和力矩的显著变化, 形成了具有内外不确定性的复杂时变非线性动力学问题, 变体飞机的这些不确定和时变的特性给控制系统的设计带来了困难[2-4]。

变体飞机属于跨学科研究, 包含有机翼结构、驱动系统、气动建模、非刚性动力学和飞行控制等领域[5]。一部分研究主要集中在变形结构的执行机构位置优化上面[6-8]。还有其他相关的研究工作体现在气动弹性分析方面[9], 以及为减少飞行控制中必须处理的动力学问题, 对变体飞机的惯性力和力矩展开研究[10]。文献[11]提出了一种适用于变体飞机动态载荷数值计算的方法。在文献[12]中, 提出了折叠翼型飞机在机翼变形过程中的线性参数变化模型, 并基于准稳态气动假设对纵向动力响应进行了数值模拟。

尽管机翼结构、驱动系统和动力学模型的发展取得了重大进展, 但要有效地控制变体飞机仍有许多工作要做。在变体飞机几何形状发生较大变化时, 气动力、力矩和质心会受到严重影响。因此变体飞机的控制系统必须能够在变形情况下, 保持整个飞行系统的稳定, 要具备良好的鲁棒性。为此, 国内外学者都开展了相关的研究。文献[13]引入了线性输入变化来描述此类系统, 并应用合成的一对线性控制器去解决线性输入变体飞行器的干扰抑制问题。文献[14]针对变翼展变体飞机进行了纵向飞行稳定性和控制的研究, 并提出了一种简单的比例状态反馈控制与特征结构分配相结合的方法。针对无尾折翼变体飞机的线性模型, 文献[15]设计了多回路的飞机变形控制器, 并提出了一种自增益H∞控制方法(self-gain scheduled H∞ controller)保证机翼过渡过程的稳定性和动态性。为了保证变体无人机在几何外形大尺度变化下仍具有良好性能, 文献[16]在变线性参数和经典方法的基础上, 设计了一种多回路控制器, 利用经典的控制方法通过内环增益来保证系统的稳定性, 同时设计了外环变参数控制器来保证控制器的动态性能。

而对于变体飞机系统中的不确定性, 大多学者运用自适应控制和神经网络控制技术进行解决, 这些技术已经发展了几十年, 广泛应用于解决系统的不确定性问题。文献[17]设计了一种基于滚动时域优化和改进的序列最小二乘参数辨识的间接自适应控制方法, 用于解决线性变体飞机动力学模型中的不确定性。文献[18]针对变体飞行器的控制设计了一种单网络自适应跟踪控制器, 不过需要采用线性系统模型离线预训练神经网络的初始权值。文献[19]基于反馈线性化的思想, 针对变体飞行器提出了一种将动态逆方法与结构模型参考自适应控制相结合的控制方法。由于变体飞机的外形设计和飞行条件的变化, 它对物理和气动参数的变化极为敏感, 典型的变体飞机表现出高度非线性动力学特性。但几乎上述控制器的设计都是基于线性模型的。

反步法作为一种强大的非线性技术, 利用其设计的控制器已经广泛应用于具有严格反馈形式的系统中。但对于传统的反步法而言, 需要面对系统建模的不确定性引起的问题, 其中之一便是非线性项微分所带来的“微分膨胀”问题。为了有效处理各子系统的系统不确定性, 文献[20-21]中采用了具有全局逼近能力的RBFNN。RBFNN作为一种单隐层神经网络, 学习收敛速度快, 具有优良的逼近能力[22]。RBFNN是具有唯一最佳逼近(克服局部极小值问题)、训练简洁、学习收敛速度快等良好性能的前馈型神经网络, 目前已证明RBFNN能够以任意精度逼近任意连续的非线性网络, 被广泛用于函数逼近、语音识别、模式识别、图像处理、自动控制和故障诊断等领域。将RBFNN运用到反步法设计的非线性控制器中, 用其去处理各子系统中的系统不确定性, 这种针对变体飞机的控制器设计思想将能有效地处理变体飞机模型不准确带来的问题。

本文针对一款变后掠翼无人飞机设计了基于RBFNN的高精度自适应反步控制器。引入微分跟踪器(tracking differentiator, TD)[23]来改善传统反步法中所存在的“微分膨胀”问题。设计了鲁棒项消除了RBFNN带来的逼近误差, 并利用Lyapunov稳定性分析方法证明了所设计的控制律能够保证闭环系统跟踪误差收敛且一致有界。通过仿真验证了该方法的优越性。

1 问题描述

本文所针对的研究对象是一款变后掠翼无人飞机, 如图 1所示。

该变体飞机推力方向沿发动机轴线且与机身轴线重合, 变体飞行器纵向模型的非线性方程组可以按照其受力情况得到如下数学描述

式中, 状态量α, γ, q, V, h分别表示飞行器的迎角、航迹角、俯仰角速率、飞行速度以及飞行高度; m, g和Iy分别表示飞行器的质量、重力加速度和其沿y轴的转动惯量; Lw, Dw, T和Mby分别为飞行器所受到的升力、阻力、推力以及俯仰力矩。值得注意的是, 气动参数和飞机的其他设计参数都是随后掠角的变化而变化, 具体说明见附录Ⅰ。

设x1=α, x2=q, x=[α q V γ h]T, u=δe, 可将变体飞行器模型改写为下面的形式

式中, Δ1, Δ2为系统的不确定项, 主要包括建模误差Δf1(x), Δf2(x), Δg1(x), Δg2(x)和外界干扰d1, d2

设计控制律使得系统输出y可以稳定跟踪输入信号yd, 主要是能够消除不确定项对系统的影响。

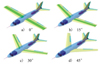thumbnail 图1

不同构型下的变体飞机

2 自适应控制律设计

2.1 相关假设

先给出一些与系统控制律设计相关的假设:

① 给定的有界参考信号yd连续可微且一阶导数有界;

② g1(x)和g2(x)可逆;

③ 系统的不确定项Δ1, Δ2有界;

④ 给定任意逼近误差上界εM, 存在理想的权值w, 该权值有上界wM, 使得RBFNN一致逼近系统中连续光滑未知的Δ, 即

式中：ε表示RBFNN的逼近误差; ŵ为RBFNN的实际权值; 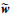为理想权值与实际权值之差。

2.2 微分跟踪器设计

在使用反步法进行设计控制律时, 需要对设计出的虚拟控制变量进行求导, 而由于模型误差和系统噪声, 使用传统微分器进行求导不可避免的会出现“微分膨胀”的问题, 而利用微分跟踪器来估计虚拟控制变量的一阶导数可以有效避免此类问题。

引理1  若输入信号r(t)分段连续可导, 且输入信号的前n-2阶导数均存在, 允许在某时刻tj(j=1, 2, …k), 输入信号的n-1阶导数不可导, 但其左导数r-(n-1)(tj)与右导数r+(n-1)(tj)均存在(同时r-(n-1)(tj)≠r+(n-1)(tj)), 则存在如下的微分跟踪器(TD)

式中，K>0, ai(i=1, 2, …, n)>0为待设计参数。且存在∂>0, l∂>n使得

式中, O((1/K)l∂-i+1)表示ζi与ri-1(t)之差是(1/K)l∂-i+1的高阶无穷小, ∂=(1-K0)/K0, K0∈[0, min(l/(l+n), 0.5)], n>2。

由(9)式可知, ζ1是r(t)的估计值, ζi是r(t)第i-1阶导数的估计值。由(10)式可知, 选取较大的参数K可以尽可能减小输入信号导数的估计误差。反步法只需要虚拟控制变量的一阶导数, 故而选取的TD为

2.3 控制律设计

Step1  考虑到系统(6)的第一个子系统ẋ1=f1(x)+g1(x)x2+Δ1, 定义虚拟反馈误差

式中，x2d为第二个子系统的虚拟控制量。

对于e1求导, 得

根据(8)式设计的RBF在线逼近系统的不确定项为

将(12)、(14)式代入(13)式可得

令第一个子系统的理想虚拟控制量为

式中，k1, σ1都为正实数。ŵ1Tv1是RBFNN输出, 用以逼近系统不确定项Δ1; σ1tanh(e1)为鲁棒项, 用以抵消RBFNN的逼近误差ε1。

本文所采用的RBFNN是一种单隐层神经网络, 学习收敛速度快, 其数学表达式为

式中:N(w, xn)=[N1(xn)…Np(xn)]∈Rp为RBFNN的输出向量; xn∈Rk为RBFNN的输入向量; w=[w1…wp]∈Rl×p为RBFNN的权值; l为RBFNN节点个数; v(xn)=[v1(xn)…vl(xn)]∈Rl, vi(xn)为基函数, 通常选择为高斯函数, 有

式中：ci∈Rk为高斯基函数中心向量; bi为高斯基函数的基宽。RBF属于线性参数化神经网络, 网络输出是基函数的线性组合, 其结构如图 2所示。

将(16)式带入(15)式可得

式中：参数k1用于调节系统的动态特性；参数σ1改善系统的鲁棒性。本文集中研究鲁棒自适应反步控制方法, 对参数的选取只是从理论上给予约束条件和证明, 在实际中利用经验和“试凑”的方法在仿真中确定这些参数。

Step2  考虑到系统(6)的第二个子系统ẋ2=f2(x)+g2(x)u+Δ2, 对e2求导可得

根据(8)式, 设计RBFNN在线逼近系统的不确定项

与x2d的设计类似, 取ud即u

式中，k2, σ2都为正实数。ŵ2Tv2是RBFNN输出, 用以逼近系统不确定项Δ2; σ2tanh(e2)为鲁棒项, 用以抵消RBFNN的逼近误差ε2。

将(22)式带入(20)式可得

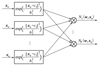thumbnail 图2

RBFNN基本结构

2.4 稳定性分析

取Lyapunov函数

对其求导得

将(19)式和(23)式代入(25)式, 整理可得

设计权值自适应律为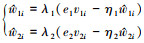, 且上式有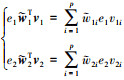, 那么(26)式可整理为

由于

故可得到

设w1和w2有上界, 满足|w1| < w1M, |w2| < w2M; ε1, ε2有上界|ε1| < ε1M, |ε2| < ε2M; 反馈误差e1, e2有下界, |e1|≥e1m≥0, |e2|≥e2m≥0。选择合适的参数k1, k2, η1, η2, σ1和σ2满足(30)式, 可确保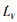 < 0, 即所设计的控制律能够保证闭环系统跟踪误差收敛且一致有界。

3 仿真验证

3.1 微分跟踪器仿真验证

本节将针对本文2.2节所引入的微分跟踪器进行仿真验证。

选择幅值为10, 频率1 rad/s的正弦波信号为输入信号, 选择噪声功率为0.1的白噪声作为噪声源, 进行仿真。经计算信号及噪声参数如表 1所示。

表1

信号数据

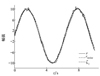thumbnail 图3

仿真结构图
thumbnail 图4

微分跟踪器原始信号量跟踪对比曲线
thumbnail 图5

微分跟踪器与传统微分器对比曲线

3.2 角速率环仿真验证

为了验证本文提出方法的优越性, 针对变体飞机纵向模态进行仿真分析。根据控制律设计的规律, 先对内环(角速率环)进行仿真验证, 对比分析效果, 接着再对外环(姿态环)进行仿真验证。

本文所研究的变体飞机质量为38 kg, 其他性能参数如表 3所示。所设计的神经网络包含50个N(w, xn)节点, 其中针对内环的输入向量设置为xninner=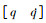, 则取高斯基函数中心向量为ciinner=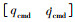; 针对外环的输入向量设置为xnouter=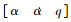, 则取高斯基函数中心向量为ciouter=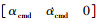。鲁棒自适应反步法控制器和微分跟踪器中的参数如表 4所示。

表3

不同构型下变体飞机参数

表4

参数列表

为了验证控制系统的鲁棒性, 在模型的标称气动参数上增加了5%, 其模型气动参数变化如下

下文将在变体飞机的固定构型和变构型2种情况下, 对比传统反步法和基于RBFNN的鲁棒自适应变体飞机反步控制方法的仿真效果。

·固定构型仿真对比

本节在变体飞机固定构型情况, 对2种方法设计的内环控制律进行仿真比较。固定后掠角构型为0°(τ=0°), 初始飞行状态设为h=1 000 m, V=30 m/s, γ=0°。给定的参考俯仰角速率指令如图 7所示, 指令在3 s后从0°/s增加到5°/s保持3 s后回归到0°/s, 在8 s时又变成-5°/s并维持3 s后恢复到0°/s。图 7展示了仿真结果。

通过对比发现, 在内环中使用本文所提出的方法相较于传统的反步法, 动态响应更快。如表 5所示, 对2种方法的俯仰角速率跟踪误差求其均方根(平方平均数), 可发现传统反步法的结果要高出本文提出方法4.892 2%, 这个结果可以反映出本文方法的优越性。

表5

固定构型下俯仰角速率跟踪误差的均方根对比

从控制器最终输出结果看, 在8.12 s时, 2种方法的出舵量出现最大偏差, 本文方法计算的升降舵出舵量高出传统反步法的4.68%。对比数据可以看出由于控制指令在第6 s和第8 s的剧烈切换, 导致控制器计算出相应的舵偏输出, 但是传统反步法的响应相对来说有所迟滞, 动态性能欠佳。

·变构型仿真对比

为了进一步测试本文提出方法的性能, 将在给定控制指令的同时对构型也进行改变。后掠角在仿真开始3 s后开始以9°/s的速率从变化0°到45°, 通过(32)式的二阶指令滤波器对其进行指令软化, 其后掠角变化曲线如图 8所示, 除此之外其他仿真条件与上节相同。

变体飞机后掠角发生变化导致整个模型发生改变, 可以将其看做被控对象的干扰项, 在变体飞机变化过程中对其进行控制考验了控制算法的鲁棒性和自适应能力。通过图 9可以看出基于RBFNN的鲁棒自适应算法能更加快速地响应模型变化过程的控制问题。传统反步法和本文提出方法的俯仰角速率跟踪误差均方根分别是0.733 4和0.705 8，相比之下传统的反步法误差要高出3.910 4%。

从控制器最终输出结果看, 在8.1 s时, 2种方法的出舵量出现最大偏差, 本文方法计算的升降舵出舵量高出传统反步法的10.36%, 印证了上文所得出的结论。

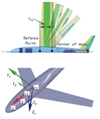thumbnail 图6

修正参数xcg与参考系定义
thumbnail 图7

固定构型下俯仰角速率变化曲线
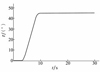thumbnail 图8

变构型下后掠角指令信号
thumbnail 图9

变构型下俯仰角速率变化曲线

3.3 姿态环仿真验证

上一节给出了本文提出方法在角速率环下的仿真测试, 但是整体算法的优越性并没有完全体现出来。俯仰角速率信号属于飞机控制系统中的快变量, 对于系统的响应比较快, 而RBFNN在线逼近系统的不确定项会需要一定的时间, 所以在内环控制上, 该方法的优势并没有完全体现出来, 所以需要在姿态环中进行仿真验证。

1) 固定构型仿真对比

固定后掠角构型为0°(τ=0°), 选择迎角增量Δαcmd=1.833°为参考指令。初始飞行状态设为h=1 000 m, V=30 m/s, 迎角指令在2 s后从初始状态增加到5°。图 10展示了仿真结果。

为了增加对比效果, 除了传统反步法和本文提出方法设计控制器以外, 还设计对内环控制使用本文方法, 外环使用传统反步法的控制器, 这3种控制器对比结果如表 6所示, 可以看出本文提出方法的跟踪误差均方根最低, 传统反步法比其高出30.414 9%, 而且调节时间耗时最短, 比传统反步法快61.82%。

表6

固定构型下俯仰角跟踪误差的均方根对比

从控制器最终输出结果看, 2种方法的出舵量在控制指令给出后的0.12 s内出舵偏差非常明显, 传统反步法的响应迟滞很明显, 动态性能欠佳。

2) 变构型仿真对比

为了进一步测试本文提出方法的性能, 将在给定控制指令的同时对构型也进行改变。后掠角的变化情况与3.2节的图 8相同, 其余仿真条件与上小节相同, 其仿真结果如图 11所示。

与上一小节的结论相同, 后掠翼的变化会对控制带来干扰, 使得控制的跟踪精度要低于固定构型, 但还是可以从仿真结果中看出基于RBFNN的鲁棒自适应算法的优越性。从表 7中可以看出在变构型下本文提出方法跟踪误差还是最低, 传统反步法比其高出30.705 3%, 而且调节时间耗时传统反步法快61.82%。

表7

变构型下俯仰角跟踪误差的均方根对比

从控制器最终输出结果看, 本文提出方法的出舵量在控制指令给出后的0.12 s内与传统反步法出舵偏差非常明显, 而这段时间也是后掠翼和控制指令同时作用的时间, 这是基于RBFNN的鲁棒自适应算法对于这段过程额外的修正, 所以比传统反步法有着更加优越的动态性能。

thumbnail 图10

迎角变化曲线
thumbnail 图11

迎角变化曲线

4 结论

本文针对变体飞机非线性模型的不确定性问题, 提出了一种基于RBFNN的鲁棒自适应方法, 经过仿真验证表明该方法能很好地跟踪期望信号并能保证控制的鲁棒性。通过自适应项和鲁棒项的引入, 该方法可以使变体飞机非线性模型对控制指令的响应快速和精确。通过Lyapunov稳定性分析, 证明该方法设计的控制律能够保证跟踪误差收敛且一致有界, 且能有效抑制系统中不确定的影响。如何根据实际需要选择整定自适应参数是下一步将要开展的内容。

附录Ⅰ气动力和气动力矩方程

由于计算CFD数据时将气动力和力矩的参考点固定在机体系中, 而变体飞机的重心是随着变体飞机后掠角的改变而改变的, 由于力线平移定理(theorem of parallel transfer the line of action of a force)可知此变化对于气动力的没有影响, 但对于飞机的气动力矩将产生巨大的影响, 所以要对飞机的气动力矩进行修正。因此作用于飞行器上的总气动力矩计算方法如下

式中，(xcg, ycg, zcg)是CFD计算参考原点与实际变体飞机质心之间的距离。

附录Ⅱ文中涉及的变量

式中，x=[αqVγh]T, x1=α, x2=q, u=δe。

References

  1. Shi R, Peng J. Morphing Strategy Design for Variable-Wing Aircraft[C]//15th AIAA Aviation Technology, Integration, and Operations Conference. 2015: 3002 [Google Scholar]
  2. Wu Z, Lu J, Rajput J, et al. Adaptive Neural Control Based on High Order Integral Chained Differentiator for Morphing Aircraft[EB/OL]. (2015-10-25)[2019-08-29]. https://www.hindawi.com/journals/mpe/2015/787931/ [Google Scholar]
  3. Seigler T M, Neal D A, Bae J S, et al. Modeling and Flight Control of Large-Scale Morphing Aircraft[J]. Journal of Aircraft, 2007, 44(4): 1077-1087 [Article] [CrossRef] [Google Scholar]
  4. Wu Z, Lu J, Zhou Q, et al. Modified Adaptive Neural Dynamic Surface Control for Morphing Aircraft with Input and Output Constraints[J]. Nonlinear Dynamics, 2017, 87(4): 2367-2383 [Article] [CrossRef] [Google Scholar]
  5. Shi R, Wan W. Analysis of Flight Dynamics for Large-Scale Morphing Aircraft[J]. Aircraft Engineering and Aerospace Technology:An International Journal, 2015, 87(1): 38-44 [Article] [Google Scholar]
  6. O'Grady B. Multi-Objective Optimization of a Three Cell Morphing Wing Substructure[D]. Dayton: University of Dayton, 2010 [Google Scholar]
  7. Johnson T, Frecker M, Abdalla M, et al. Nonlinear Analysis and Optimization of Diamond Cell Morphing Wings[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(7): 815-824 [Article] [CrossRef] [Google Scholar]
  8. Joo J J, Sanders B Optimal Location Of Distributed Actuators Within an In-Plane Multi-Cell Morphing Mechanism[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(4): 481-492 [Article] [CrossRef] [Google Scholar]
  9. Andersen G, Cowan D, Piatak D. Aeroelastic Modeling, Analysis and Testing of a Morphing Wing Structure[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2007: 1734 [Google Scholar]
  10. Seigler T, Neal D, Inman D. Dynamic Modeling of Large-Scale Morphing Aircraft[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2006: 1893 [Google Scholar]
  11. Obradovic B, Subbarao K Modeling of Flight Dynamics of Morphing Wing Aircraft[J]. Journal of Aircraft, 2011, 48(2): 391-402 [Article] [CrossRef] [Google Scholar]
  12. Yue T, Wang L, Ai J. Longitudinal Linear Parameter Varying Modeling and Simulation of Morphing Aircraft[J]. Journal of Aircraft, 2013, 50(6): 1673-1681 [Article] [CrossRef] [Google Scholar]
  13. Boothe K, Fitzpatrick K, Lind R. Controllers for Disturbance Rejection for A Linear Input-Varying Class of Morphing Aircraft[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 2005: 2374 [Google Scholar]
  14. Beaverstock C S, Ajaj R, Friswell M I, et al. Effect of Span-Morphing on the Flight Modes, Stability & Control[C]//AIAA Guidance, Navigation, and Control (GNC) Conference, 2013: 4993 [Google Scholar]
  15. Yue T, Wang L, Ai J. Gain Self-Scheduled H∞ Control for Morphing Aircraft in the Wing Transition Process Based on an LPV Model[J]. Chinese Journal of Aeronautics, 2013, 26(4): 909-917 [Article] [CrossRef] [Google Scholar]
  16. Baldelli D H, Lee D H, Sánchez Peáa R S, et al. Modeling and Control of an Aeroelastic Morphing Vehicle[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1687-1699 [Article] [CrossRef] [Google Scholar]
  17. Gandhi N, Jha A, Monaco J, et al. Intelligent Control of a Morphing Aircraft[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2007: 1716 [Google Scholar]
  18. Nobleheart W, Shivanapura Lakshmikanth G, Chakravarthy A, et al. Single Network Adaptive Critic(SNAC) Architecture for Optimal Tracking Control of a Morphing Aircraft during a Pull-up Maneuver[C]//AIAA Guidance, Navigation, and Control Conference, 2013: 5003 [Google Scholar]
  19. Valasek J, Lampton A, Marwaha M. Morphing Unmanned Air Vehicle Intelligent Shape and Flight Control[EB/OL].(2009-04-15)[2019-08-29]. https://www.researchgate.net/publication/228644798_Morphing_Unmanned_Air_Vehicle_Intelligent_Shape_and_Flight_control [Google Scholar]
  20. Chenliang W, Yan L. Adaptive Dynamic Surface Control for Linear Multivariable Systems[J]. Automatica, 2010, 46(10): 1703-1711 [Article] [CrossRef] [Google Scholar]
  21. Liu Y J, Chen C L P, Wen G X, et al. Adaptive Neural Output Feedback Tracking Control for a Class of Uncertain Discrete-Time Nonlinear Systems[J]. IEEE Trans on Neural Networks, 2011, 22(7): 1162-1167 [Article] [CrossRef] [Google Scholar]
  22. Chen M, Tao G, Jiang B. Dynamic Surface Control Using Neural Networks for a Class of Uncertain Nonlinear Systems with Input Saturation[J]. IEEE Trans on Neural Networks and Learning Systems, 2014, 26(9): 2086-2097 [Article] [CrossRef] [Google Scholar]
  23. Cao C, Hovakimyan N. Novel L1 Neural Network Adaptive Control Architecture with Guaranteed Transient Performance[J]. IEEE Trans on Neural Networks, 2007, 18(4): 1160-1171 [Article] [CrossRef] [Google Scholar]

All Tables

表1

信号数据

In the text
表3

不同构型下变体飞机参数

In the text
表4

参数列表

In the text
表5

固定构型下俯仰角速率跟踪误差的均方根对比

In the text
表6

固定构型下俯仰角跟踪误差的均方根对比

In the text
表7

变构型下俯仰角跟踪误差的均方根对比

In the text

All Figures

thumbnail 图1

不同构型下的变体飞机
In the text
thumbnail 图2

RBFNN基本结构
In the text
thumbnail 图3

仿真结构图
In the text
thumbnail 图4

微分跟踪器原始信号量跟踪对比曲线
In the text
thumbnail 图5

微分跟踪器与传统微分器对比曲线
In the text
thumbnail 图6

修正参数xcg与参考系定义
In the text
thumbnail 图7

固定构型下俯仰角速率变化曲线
In the text
thumbnail 图8

变构型下后掠角指令信号
In the text
thumbnail 图9

变构型下俯仰角速率变化曲线
In the text
thumbnail 图10

迎角变化曲线
In the text
thumbnail 图11

迎角变化曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.