| Issue |
JNWPU
Volume 41, Number 6, Decembre 2023
|
|
|---|---|---|
| Page(s) | 1064 - 1072 | |
| DOI | https://doi.org/10.1051/jnwpu/20234161064 | |
| Published online | 26 February 2024 | |
Rapid ascent trajectory optimization of rocket-based combined cycle hypersonic vehicle
RBCC高超声速飞行器上升段轨迹快速优化
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
COMAC Flight Test Center, Shanghai 201323, China
Received:
13
September
2022
The ascent trajectory design of a rocket-based combined cycle (RBCC) hypersonic vehicle has many typical characteristics, including the complex working mode of the RBCC power system, strong coupling between thrust and flight state, strong nonlinear model and many complex constraints etc. This paper proposes a rapid trajectory optimization method based on sequential convex optimization to optimize the complex ascent trajectory with the RBCC power system. Firstly, a mathematical model for optimizing the ascent trajectory of the RBCC hypersonic vehicle is established to describe the angle of attack control system with and without the second-order lag. Then, the optimization model is made convex and discretized based on the convex optimization theory, and a trajectory optimization strategy is improved. Finally, taking the maximum terminal mechanical energy as optimization objective, the ascent trajectory optimization is simulated in cases with and without the second-order lag in the angle of attack control system. The simulation results show that the proposed mathematical model and the ascent trajectory optimization method are rapid and reliable and that the optimization results meet the characteristics of the RBCC power system and provide reference for the application of a RBCC power system and the design of an angle of attack control system.
摘要
针对火箭基组合循环(RBCC)高超声速飞行器上升段轨迹设计所具有的动力系统工作模态复杂、推力与飞行状态存在强耦合、模型强非线性且存在多种复杂约束限制等典型特征, 设计了一种基于序列凸优化的RBCC动力上升段轨迹快速优化方法。针对攻角控制系统是否存在二阶滞后情况, 分别建立了适用于RBCC高超声速飞行器上升段轨迹优化的数学模型。基于凸优化理论对原优化模型进行凸化和离散化处理, 进而设计了改进的轨迹优化求解策略。以末端机械能最大为优化指标, 针对攻角控制系统存在/不存在二阶滞后的情况分别进行了上升段轨迹优化仿真。结果表明, 所构建模型和轨迹优化方法可以快速、有效地完成RBCC高超声速飞行器上升段轨迹优化, 优化结果符合RBCC动力系统工作特点, 且可为RBCC动力运用和攻角控制系统设计提供参考。
Key words: rocket-based combined cycle / hypersonic vehicle / ascent trajectory optimization / sequential convex optimization / second-order lag of control system
关键字 : RBCC / 高超声速飞行器 / 上升段轨迹优化 / 序列凸优化 / 控制系统二阶滞后
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来,高超声速飞行器的多样化发展和复杂任务需求对助推上升段动力系统的设计提出了许多新的要求,如较强的短时加速、全程多次开关机、宽域工作能力等。与传统火箭动力相比,火箭基组合循环(rocket based combined cycle, RBCC)动力系统将高推重比、低比冲的火箭发动机和低推重比、高比冲的冲压发动机有机地组合在一起,具有低成本、技术先进、使用灵活等特征,可用于执行广空域、宽速域运载及新质作战等飞行任务[1-2]。
然而,RBCC动力系统的引入给高超声速飞行器的上升段轨迹设计带来了新的挑战[3-4]。首先,RBCC动力系统工作模态多,各模态性能迥异、动态切换;其次,上升段状态参数变化范围大,动力性能与飞行状态耦合程度高,且面临多种复杂的过程及终端约束限制。上述因素使得上升段轨迹设计的可行域极小、设计难度极大,传统火箭助推运载器的轨迹设计方法和经验规律已难以胜任,有必要针对其动力系统特点开展相应的数值优化求解算法及策略研究。
目前,典型的上升段轨迹优化方法可分为间接法[5]和直接法[6-9]。其中,间接法由于模型精度低、通用性不高且收敛性较差,难以应用于具有复杂、高保真模型的RBCC上升轨迹优化问题。随着计算机技术的发展,直接法中的配点法、伪谱法以及粒子群等数值优化方法在上升段轨迹优化设计中得到广泛应用[6-9],然而,上述方法均未能满足上升段轨迹快速优化的需求。因此,为提升轨迹优化设计的计算效率,部分学者将凸优化方法[10-14]引入上升段轨迹设计中。Szmuk等[12]以推力方向作为控制量,利用无损凸化技术求解运载火箭上升段轨迹优化问题,但其忽略了运载器所受升力。Liu等[13]将推力方向和气动系数作为控制量,但考虑的气动力模型较为简单。王嘉炜等[14]在对固体火箭助推飞行器轨迹优化问题进行建模时,选择攻角作为唯一控制量,有效处理了飞行器气动力的计算。虽然基于凸优化的方法已逐步用于解决上升段轨迹设计问题,然而现有公开文献较少涉及RBCC动力上升段轨迹优化问题。
因此,本文以RBCC动力高超声速飞行器为研究对象,提出了一种考虑复杂约束、高非线性及强耦合模型限制的动力上升段轨迹快速优化方法。针对攻角控制系统是否存在二阶滞后情况,构建了完整的RBCC动力上升段轨迹优化模型;设计了基于序列凸优化的上升段轨迹快速优化策略及算法。仿真结果表明,该方法在保证可行性的同时,突破了传统轨迹优化方法求解该类复杂约束问题时效率低或无法找到可行解的局限,能够提高RBCC动力飞行器的轨迹优化设计效率。
1 上升段轨迹优化问题描述
1.1 上升段运动模型
考虑飞行器的上升段运动主要保持在纵向平面内, 故不考虑侧向运动。假设地球为不旋转圆球, 建立纵向平面内上升段质心运动方程
式中:r, V, θ, m, α, g, ms, P, D, L分别为地心距、速度、当地弹道倾角、飞行器质量、攻角、当地重力加速度、发动机燃料秒流量、推力、气动阻力及升力。对于上述模型而言, 其状态量 x =[r, V, θ, m]T, 控制量 u =[α, ms]T。
若考虑攻角控制存在二阶滞后, 则攻角实际值与指令值并不完全一致。此时, 补充如下方程
式中:αc, 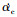 ,
, 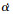 分别为飞行器的攻角指令值、指令变化率和实际攻角变化率; ξ为控制系统阻尼系数, ωn为自然频率。该模型引入实际攻角和攻角变化率作为新的状态量, 同时引入
分别为飞行器的攻角指令值、指令变化率和实际攻角变化率; ξ为控制系统阻尼系数, ωn为自然频率。该模型引入实际攻角和攻角变化率作为新的状态量, 同时引入 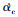 作为控制量, 此时, x =[r, V, θ, m, α, β]T, u =[αc, ms]T。
作为控制量, 此时, x =[r, V, θ, m, α, β]T, u =[αc, ms]T。
气动力D, L可由(3)式计算得到
式中:q=0.5ρV2为飞行动压;ρ为大气密度;Sref为飞行器气动参考面积;升、阻力系数CL, CD均为高度、攻角和马赫数的函数, 可通过插值得到。
本文研究的高超声速飞行器采用RBCC动力系统助推, 该系统由火箭发动机与冲压发动机分系统组合而成, 因此, 其推力与燃料秒流量可表示为
式中:msr和msa分别为火箭发动机和冲压发动机的燃料秒流量;PR和PA分别代表火箭发动机与冲压发动机推力。
火箭发动机推力PR计算如(5)式所示
式中, Ispr为火箭发动机比冲, 可表征为关于高度的函数fIspr(h)。
冲压发动机推力计算为
式中, S, Er, φ, Ispa分别为冲压发动机进气道横截面积、燃油流量比、流量系数及比冲。可见, 冲压推力与高度、马赫数、攻角及发动机参数均相关, 即动力性能与飞行状态存在高度的非线性和强耦合关系。
为避免人为划分模态引起的性能下降, 本文暂不给定模态划分准则, 而是将火箭发动机燃料秒耗量msr作为全程控制量, 进而通过轨迹优化设计获得其控制规律, 以及RBCC动力系统的工作模态转换准则和机理。考虑模型试验数据信息和燃料化学特性, 本文暂取Er=0.068。此外为提升指令光滑度, 本文引入攻角变化率 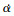 作为伪控制量, 攻角α可视为增广的状态量, 故此时的控制量选择为
作为伪控制量, 攻角α可视为增广的状态量, 故此时的控制量选择为 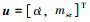 。类似地, 对于(2)式描述的考虑攻角控制系统存在二阶滞后的情况, 控制量可选为
。类似地, 对于(2)式描述的考虑攻角控制系统存在二阶滞后的情况, 控制量可选为 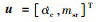 。
。
1.2 约束条件描述
对于上升段轨迹优化设计而言, 主要考虑过程参数、状态及控制量等约束的限制。典型过程约束包括动压q、法向过载n、驻点热流密度 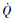 , 具体为
, 具体为
式中: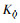 为热流密度常数, 其取值与飞行器气动外形相关;qmax, nmax及
为热流密度常数, 其取值与飞行器气动外形相关;qmax, nmax及 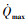 分别为动压、法向过载和热流密度允许峰值。
分别为动压、法向过载和热流密度允许峰值。
从实际可行性以及安全飞行角度考虑, 状态变量亦需要满足一定的约束, 即有
综合考虑飞行性能、控制系统性能和发动机性能, 可建立控制变量约束模型, 有
此外, 对于本文研究的问题而言, 端点约束可分为初始约束与终端约束, 即有
1.3 优化问题描述
为挖掘飞行器运载潜力, 将优化目标选取为上升段末端机械能最大, 优化目标可以表示为
综上, RBCC上升段轨迹优化问题可以描述为: 寻找最佳状态量 x (t)及控制量 u (t), 使得目标函数(11)式最大, 同时满足状态方程约束(1)或(2)式, 以及各类约束(7)~(10)式。
为了提升优化求解的收敛性, 往往需要对模型进行无量纲化处理, 限于篇幅, 此处不再赘述。
2 基于凸优化的求解框架及策略设计
典型凸优化问题即为寻找最优控制量, 使得
式中, 目标函数f0(x)和不等式约束函数fi(x)都是凸函数, 而等式约束函数hj(x)=ajTx-bj是仿射函数。显然, RBCC高超声速飞行器上升段轨迹优化设计是一个高度非线性的最优控制问题, 无法直接采用凸优化方法求解, 因此需要先对该优化问题模型进行转化。
2.1 时间自由问题转化处理
对于上升段总飞行时间未知的这类时间自由问题, 首先定义新的自变量τ∈[0, 1]和控制量ut=tf-t0, 并且将原问题的时间区间映射到[0, 1]上, 得到
同时, 将原自变量时间作为新的状态变量, 则有
以姿态控制系统理想情况为例, 原状态量为 x =[r, V, θ, m, α]T, 运动微分方程记为 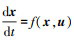 , 则以τ为自变量的运动方程表达为
, 则以τ为自变量的运动方程表达为
记x =[r, V, θ, m, α, t]T, 则增广后的新动力学微分方程可记为
2.2 凸化处理
考虑到前述上升段轨迹优化模型是非凸的, 将其进行凸化处理是应用凸优化技术数值求解的关键。本节以姿态控制理想情况下上升段轨迹优化问题为例采用逐次线性化等[11]技术进行模型凸化。
1) 动力学方程凸化
首先, 设第k次迭代优化的参考轨迹为(xk, uk, utk), 具体可表述为
取其作为初始参数序列, 将动力学方程(16)在该参考状态序列下进行一阶泰勒展开, 得到线性化的动态方程约束, 即
式中:Ak, B1k, B2k为雅可比矩阵,具体推导方法可参考文献[15];Ck为补充项,其表达式为Ck=f-Ak-xk-B1kuk-B2kutk。
同时,为保证线性化的有效性和精度,需引入信赖域约束:
式中,δx表示信赖域半径。
其动态方程约束可类比得到, 此处不做赘述。
2) 过程约束处理
类似地, 驻点热流密度、动压、过载等过程约束同样需要在参考轨迹附近进行线性化。记 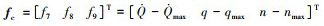 , 过程约束可改写为
, 过程约束可改写为
对其进行线性化可得
式中, Cpk=fc-Apkxk, Apk为偏导数矩阵。
3) 指标函数凸化处理
记机械能公式
为非凸形式。同理, 采用逐次线性化方法, 可将其转化为
式中, 偏导数矩阵AJk和常数矩阵CJk的表达式不再专门给出。
此外, 注意到状态量和控制量表达(8)~(10)式均为凸形式, 故无需做凸化处理。至此, 该上升段轨迹优化即转化为一典型的凸问题。
2.3 离散化处理
为了应用数值方法对上述凸化后的问题进行求解, 需要对状态量和控制量进行离散化处理。将自变量变化域[τ0, τf]等间距离散为M个间隔, 自变量离散为τ0, τ1, …, τM, 状态量x离散为x0, x1, …, xM, 控制量 u离散为u0, u1, …, uM。
采用梯形法则[11]对(18)式进行离散, 可得
上标k表示第k次迭代, m表示离散点编号, m=0, 1, …, M; Δτ=(τf-τ0)/M。
类似地, (22)式的离散化形式为
控制变量约束、状态变量约束的离散形式为
状态变量的端点条件可以进一步表述为
综上所述, 原轨迹优化问题转化为参数化凸问题, 可表示为如下形式
2.4 凸优化求解策略改进及流程
1) 终端约束处理
考虑终端高度等端点等式约束, 若在优化求解过程中直接限制为固定值, 初期迭代过程中很难满足该约束, 甚至会出现不可行解进而导致优化失败。因此, 可将这类约束转化为性能指标中的惩罚项[11]
式中:常系数ci>0, i为终端等式约束序号;I为约束总数量。考虑该惩罚项为非凸形式, 故通过引入松弛矢量 R, 将其转化为(31)式的形式引入性能指标中
对应的松弛约束为
其他终端等式约束即可采用该方法进行处理。
于是, 上述参数化凸问题可松弛为
2) 优化求解流程
考虑到上述凸化后的问题与原轨迹优化问题之间存在偏差, 通过序列凸优化算法[15]迭代求解上述凸问题可逐步逼近原问题的解。
为保证线性化的有效性和解的收敛性及精度, 迭代过程以当前优化轨迹不断更新参考轨迹, 并以相邻2次迭代的凸优化解对应的状态量最大偏差作为收敛准则, 即
式中, ε为收敛误差限。
此外, 为了提升迭代寻优的收敛快速性, 本文基于回溯搜索方法对信赖域 δx进行动态调整[14], 可得基于序列凸优化的上升段轨迹优化算法流程如图 1所示, 描述如下:
1) 设k=0, 选取一条初始轨迹(xk, uk, utk, Rk);
2) 基于参考轨迹构建凸问题(33), 求解该问题得到序列最优解(xk+1, uk+1, utk+1, Rk+1);
3) 判断是否满足(34)式和回溯搜索条件, 若满足, 则优化结束; 否则, 令k=k+1, 转入步骤2);
4) (xk+1, uk+1, utk+1)即是全局最优状态轨迹和最优控制变量。
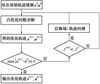 |
图1 基于序列凸优化的上升段轨迹优化求解流程图 |
3 算例仿真及分析
3.1 仿真条件
以某型RBCC高超声速飞行器概念验证机为例进行仿真。飞行器初始质量4 t, RBCC助推级共携带燃料3.2 t。飞行器由载机水平投放, 初始高度为10.5 km, 速度为388.9 m/s, 飞行攻角为3°。终端约束为: 终端高度大于50 km且终端马赫数大于11。优化目标为终端机械能最大。主要约束设置为: nmax=3, qmax=200 kPa, 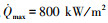 , α∈[-2°, 10°],
, α∈[-2°, 10°], 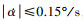 , msr∈[0, 40] kg/s。
, msr∈[0, 40] kg/s。
综合考虑计算效率与解的精度, 本文仿真过程中共取61个离散点, 序列凸优化算法的初始信赖域和收敛误差限设置为
此外, 回溯搜索算法中的2个参数均取0.8[15]。
所有仿真均在搭载Intel Core i7-8700 3.20 GHz Intel处理器的台式机完成, 仿真环境为MATLAB 2016b平台, 基于CVX工具包进行轨迹优化算法开发, 并调用SDPT3求解器求解凸优化子问题。
3.2 攻角控制系统理想情况下的上升段轨迹优化
将控制系统理想情况下轨迹优化模型简记为模型一, 针对该模型进行终端机械能最大的上升段轨迹优化。凸优化算法经过12轮迭代后收敛, 每轮迭代约耗时1.8 s, 优化过程共耗时19.88 s, 优化结果如图 2~3所示。
分析仿真结果可知, 上升段共飞行135.66 s, 终端质量为800 kg, 终端高度为62.08 km, 速度为4 866.99 m/s, 满足终端约束; 动压、过载、驻点热流密度均满足给定的过程约束限制。将所得控制量进行插值后代入运动方程进行积分, 所得积分结果与优化结果对应的状态相对偏差小于0.1%, 验证了优化结果的可行性, 表明本文所提序列凸优化方法可逼近原轨迹优化问题的解。图 2~3中虚线为凸优化所使用的初始猜测轨迹, 本文仅将初始猜测轨迹取为初、末端状态猜测值的连线, 这种情况下,凸优化方法仍能有效、快速地收敛至优化结果。可见, 本文所设计的优化算法和求解策略可以快速、有效地求解RBCC高超声速上升这一复杂、非线性、强耦合的非凸最优控制问题。
此外, 结合仿真结果可知, 对于该问题而言, 上升段飞行主要可分为3段。第一段为0~22 s, 此时飞行马赫数较低, 因此冲压发动机推力小、效率低, RBCC动力系统工作在冲压+火箭混合模态, 且以火箭加速为主, 此时马赫数逐渐增加, 但飞行高度变化较小。第二段为22~91 s, 该段飞行高度、马赫数都较适宜冲压发动机工作, 故此时火箭发动机关机, RBCC动力系统工作在冲压模态, 飞行马赫数和高度均缓慢变化, 直至爬升至约30 km, 飞行器在该段将达到动压约束边界并保持约17 s。第三段对应为91 s至上升段结束, 此时由于高度较高, 冲压发动机效率逐步降低, RBCC动力系统先工作在冲压+火箭混合模态, 后逐步过渡到纯火箭模态直至燃料耗尽, 此时飞行高度和马赫数快速增加。事实上, 这种火箭动力峰-谷-峰的工作过程能够最大限度地发挥火箭发动机工作范围广和冲压发动机推进效率高的优势, 从而使飞行器能够在燃料一定的情况下获得更大终端高度、马赫数, 即实现终端机械能最大。
此外, 为探究离散点数选取对凸优化算法精度及计算效率的影响, 取31和91个离散点分别进行轨迹优化, 并利用所得优化控制量进行积分, 所得优化及积分结果对比如表 1所示。
不同离散点数量优化及积分结果对比
由表 1可知, 3组优化结果的迭代次数基本一致, 而随着离散点数的增加, 计算耗时有所增加, 优化解与积分解之间的误差显著降低, 表明优化解的可行性逐渐提升。相较于离散点取61与91的情况, 离散点取31时, 终端状态的优化解与积分解误差较大, 表明该组优化结果不可行; 而相较于离散点91的情况, 离散点取61的优化结果在精度基本相当情况下, 计算耗时减少了30%。因此, 综合考虑计算效率和精度, 取离散点为61较为合适。
 |
图2 模型一对应的部分状态量优化结果 |
 |
图3 模型一对应的控制量优化结果 |
3.3 考虑攻角控制系统二阶滞后上升段轨迹优化
将考虑控制系统二阶滞后的轨迹优化模型简记为模型二, 针对该模型进行上升段轨迹优化。仿真中, 取阻尼比ξ=0.7, 固有频率ωn=0.5。凸优化算法经过13轮迭代后收敛, 每轮迭代约耗时1.8 s, 优化过程共耗时23.08 s, 优化结果如图 4~5所示。
由结果可知, 上升段共飞行136.20 s, 剩余质量为800 kg, 终端高度为62.18 km、飞行马赫数为15.59, 满足终端约束, 动压、过载、驻点热流密度均满足给定的过程约束限制。
由图 4可知, 模型一、二的优化结果较为接近, 而由图 4d)的优化曲线可知, 模型二的弹道倾角变化存在一定滞后, 尤其是在飞行前中期的几个拐点位置, 考虑是控制系统滞后导致实际攻角变化滞后于模型一, 这一点亦可从图 4e)的攻角指令曲线得以印证。
由图 5a)可知, 模型二的攻角变化率总是提前模型一变化, 考虑是模型二控制系统存在二阶滞后, 需要提前改变控制指令, 以补偿滞后效应, 使实际攻角曲线尽可能逼近模型一的最优结果。此外, 模型一终端机械能为952 380 kJ, 模型二终端机械能为952 310 kJ, 略低于模型一。可见, 模型二的控制滞后牺牲了一定的最优性。
为进一步探究自然频率ωn取值对轨迹的影响, 分别取ωn=0.1, ωn=0.9进行仿真, 结果如图 6及表 2所示。由表 2可知, 相较于理想情况, 考虑控制系统二阶滞后特性轨迹优化结果的最优性有所降低, 且最优性随着ωn的增大而提升。由图 6可知, 当ωn较小时, 攻角曲线较为光滑, 此时实际攻角对攻角指令的响应速度较慢, 攻角变化较指令值滞后情况明显, 因此需要提前给出指令信号以更好地操纵飞行。当ωn较大时, 实际攻角对攻角指令的跟踪效果更好, 此时飞行器具有较好的操纵性。通常来说, 飞行器自然频率由其静稳定性决定, 但设计控制系统时, 一般情况下要求自然频率低于自动驾驶仪频率以免出现共振。同时, 由于控制系统的超调量及振荡次数均只与阻尼比ξ相关, 而实际攻角的最大峰值并未超过指令攻角, 因此设计姿态控制系统时应依据实际需要进行控制参数选择。
不同ωn取值优化结果
 |
图4 考虑控制滞后的状态量优化结果 |
 |
图5 考虑控制滞后的控制量优化结果 |
 |
图6 不同ωn取值优化结果攻角对比 |
4 结论
针对RBCC高超声速上升段轨迹快速优化问题,本文设计了一种基于序列凸优化的轨迹优化算法和策略,相关结论如下:
1) 所设计优化算法可以快速、有效地求解复杂工作模态下RBCC高超声速上升这一复杂、非线性、强耦合的非凸最优控制问题;
2) RBCC发动机火箭模态峰-谷-峰的工作过程能够最大限度地结合并发挥火箭发动机工作范围广和冲压发动机经济性高的优势,从而使飞行器在燃料更省的情况下获得更大的终端高度、马赫数。
3) 相较于理想情况,考虑控制系统二阶滞后特性轨迹优化结果的最优性有所降低,且降低程度与自然频率ωn有关,设计姿态控制系统时应依据实际需要进行控制参数选择。
References
- GONG C, CHEN B, GU L. Design and optimization of RBCC powered suborbital reusable launch vehicle[C]//Proceedings of AIAA International Space Planes & Hypersonic Systems & Technologies Conference, 2013 [Google Scholar]
- WANG Yajun, HE Guoqiang, QIN Fei, et al. Research progress of rocket based combined cycle engines[J]. Journal of Astronautics, 2019, 40(10): 1126–1133 (in Chinese) [Google Scholar]
- RUAN Jiangang, HE Guoqiang, LYU Xiang. Trajectory optimization method in two-stage-to-orbit RBCC-RKT launch vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1284–1291 (in Chinese) [Google Scholar]
- LYU Xiang, HE Guoqiang, LIU Peijin. Ascent trajectory design method for RBCC-powered vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7) 1332–1337 (in Chinese) [Google Scholar]
- LI Huifeng, LI Zhaoying. Indirect method of optimal ascent guidance for hypersonic vehicle[J]. Journal of Astronautics, 2011, 32(2): 297–302 (in Chinese) [Google Scholar]
- DEREK J, DRISCOLL F. Minimum-fuel ascent of a hypersonic vehicle using surrogate optimization[J]. Journal of Aircraft, 2014, 51(6): 1973–1986 [Article] [CrossRef] [Google Scholar]
- WEI J L, TANG X J, YAN J. Costate estimation for a multiple-interval pseudospectral method using collocation at the flipped Legendre-Gauss-Radau points[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 12: 1–15 [Google Scholar]
- ZHOU H Y, WANG X G, BAI Y L, et al. Ascent phase trajectory optimization for vehicle with multi-combined cycle engine based on improved particle swarm optimization[J]. Acta Astronautica, 2017, 140: 156–165 [Article] [CrossRef] [Google Scholar]
- YANG S B, CUI T, HAO X Y, et al. Trajectory optimization for a ramjet-powered vehicle in ascent phase via the Gauss pseudospectral method[J]. Aerospace Science and Technology, 2017, 67: 88–95 [Article] [CrossRef] [Google Scholar]
- LU Ping, LIU Xinfu. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 750–765 [Article] [CrossRef] [Google Scholar]
- LIU Xinfu, LU Ping, PAN Binfeng. Survey of convex optimization for aerospace applications[J]. Astrodynamics, 2017, 1(1): 23–40 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- SZMUK M, ACIKMESE B, Berning A W. Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints[C]//Proceedings of AIAA Guidance, Navigation, & Control Conference, 2016 [Google Scholar]
- LIU Xinfu. Fuel-optimal rocket landing with aerodynamic controls[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(1): 65–76 [Article] [CrossRef] [Google Scholar]
- WANG Jiawei, ZHANG Ran, HAO Zeming, et al. Real-time trajectory optimization for hypersonic vehicles with Proximal-Newton-Kantorovich convex programming[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(11): 121–130 (in Chinese) [Google Scholar]
- YANG Ben, LI Tianren, MA Xiaoyuan. Fast multi-constraints trajectory optimization based on sequence convex optimization[J]. Aerospace Control, 2020, 38(3): 25–30 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 基于序列凸优化的上升段轨迹优化求解流程图 |
| In the text | |
 |
图2 模型一对应的部分状态量优化结果 |
| In the text | |
 |
图3 模型一对应的控制量优化结果 |
| In the text | |
 |
图4 考虑控制滞后的状态量优化结果 |
| In the text | |
 |
图5 考虑控制滞后的控制量优化结果 |
| In the text | |
 |
图6 不同ωn取值优化结果攻角对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


