| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1266 - 1274 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861266 | |
| Published online | 02 February 2021 | |
Hurdle-Hop Simulation of Tilt-Rotor Aircraft Based on Optimal Control Theory
基于最优控制理论的倾转旋翼机跃障飞行仿真
Science and Technology on Rotorcraft Aeromechanics Laboratory, China Helicopter Research and Development Institute, Jingdezhen 333001, China
Received:
19
February
2020
Aiming at simulating the hurdle-hop of tilt-rotor aircraft in forward flight near the ground, two models of numerical simulation and analysis based on optimal control theory were proposed. Firstly, Longitudinal flight dynamic model for tilt-rotor was modified considering the influence of ground effect. Secondly, the first model is combined with predicted trajectory from inverse simulation method, the inverse model of hurdle-hop of tilt-rotor is established based on optimal trajectory, and the second model is the optimal control model of unpredicted trajectory, which is formulated from the reasonable function of objective, path and boundary constraints for hurdle-hop with detailed analysis, solved two models by direct multiple shooting method and nonlinear programming algorithm. Finally, XV-15 as the sample vehicle. Two models for hurdle-hop based on optimal control theory was calculated, the history of optimal flight trajectory and control are given.
摘要
针对倾转旋翼机近地面跃障飞行仿真分析需求,提出了2种基于最优控制理论的倾转旋翼机跃障机动数值仿真分析模型。首先,基于倾转旋翼机纵向飞行动力学模型进行地面效应影响修正;其次,模型一结合逆仿真的预定轨迹方法,建立跃障飞行最优化轨迹逆解模型,模型二针对跃障机动进行详细解析,制定合理跃障飞行的目标、路径约束和边界约束条件,构建出倾转旋翼机跃障飞行无预定轨迹的最优控制模型;并采用直接多重打靶法和非线性规划算法进行求解;最后,以XV-15为研究对象,针对2种最优控制模型进行跃障飞行仿真分析,给出了2种模型的最优化飞行和操纵的时间历程。
Key words: hurdle-hop / tilt-rotor / optimal control / nonlinear programming
关键字 : 跃障机动 / 倾转旋翼机 / 最优控制 / 非线性规划
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
倾转旋翼机兼顾直升机和固定翼特征, 其性能指标超越常规直升机, 是新一代高速直升机的主要竞争者。第三代倾转旋翼机V-280在V-22倾转旋翼机的基础上进行技术升级, 提升了低速飞行机动性并进一步提升运输效率和航程[1], 有望成为美军下一代武装军用旋翼机。
在对敌攻击任务中, 倾转旋翼机可充分发挥自身的优势, 通过超低空贴地机动飞行, 利用地形地物躲过敌方侦察, 对目标实施突然袭击。在复杂地形和外部环境威胁的条件下, 执行何种飞行轨迹和操纵策略对提高突防成功率和生存率具有决定性的影响。
倾转旋翼机的机动飞行仿真研究对武装型倾转旋翼机设计具有特殊意义。对于机动飞行, 必须用非线性系统描述, 按照旋翼机完成某一特定的机动动作的轨迹反求驾驶员的输入规律, 对于倾转旋翼机的总体设计、机动性评估具有重要的参考价值。
目前飞行数值仿真的研究较多, 方法多样, 也较为成熟。在旋翼机的机动仿真过程中, 驾驶员的操纵输入历程需要进行确定。飞行器操纵输入的确定可采用预定操纵输入[2-3]、飞行控制[4-7]、或逆解[8-11]等方法, 由于旋翼机的高度耦合性及非线性特征, 预定操纵输入(相对逆解等方法, 也称为前向仿真)仅适用于相对简单的机动过程; 飞行控制方法诸如PID控制[4]、H∞[5]及神经网络等非线性控制方法[6-7], 针对预定轨迹与计算轨迹之间的差异性进行解算,调整飞行器的操纵输入, 该类方法的计算设置相对简单高效, 但对预定轨迹的准确性要求过高, 且难以处理多样化的约束。
传统逆解方法中的差分算法和积分算法[8-10]同样是针对预定轨迹进行解算操纵输入, 在匹配预定的飞行轨迹过程中将仿真过程划分为非常小的时间步长, 在每个步长上进行控制变量的计算。汪正中等[11]将轨迹优化算法纳入逆解法, 轨迹优化算法本质为最优控制问题的解算, 旨在考虑从开始到结束的整个飞行轨迹和操纵输入, 调整飞行器达到预期的飞行轨迹或系列要求。轨迹优化法适用性较强, 该方法可不直接定义飞行轨迹, 而是将机动飞行过程中的限制或要求转化为优化约束, 以计算出机动飞行过程中的操纵输入和飞行轨迹等。因此基于最优控制方法非常适用于研究美国航空设计标准(ADS-33)中的飞行任务单元(MTES)[12]以及其他机动飞行。
差分算法是将一组非线性微分方程组转换为非线性的代数方程组, 直接求解此代数方程组就可得到未知量, 该方法是由Thomson和Bradley[8]率先提出, 随后WHalley[9]利用该方法进行了人在环的飞行仿真研究。积分方法, 在每个时间步长上初始状态和控制量已知, 基于Newton迭代或优化算法消除时间步长末端的预定轨迹和计算轨迹误差, 该方法由Hess[10]提出。
轨迹优化方法, 考虑飞行器整个运动过程的飞行轨迹, Lee和Kim[13]将逆仿真问题转化为等式约束的最优控制问题。Celi[14-15]提出了基于最优化理论的逆解方法, 以飞行轨迹或机动约束(限制条件)建立无约束增广目标函数最优控制模型, 该方法的优势在于不依赖于既定的飞行轨迹和具有良好的通用性, 但对于路径中的约束处理偏弱。
2类逆解方法成功运用在直升机机动飞行的研究, 并得了一系列的成果[13-17]。在实际的机动飞行仿真问题中, 大量机动飞行并不能用飞行轨迹的方式进行定义。因此基于最优控制理论的优化飞行轨迹方法快速发展, 但目前主要侧重于旋翼机特殊性能分析研究[18-20], 基于最优控制理论的旋翼机机动飞行数值仿真研究则相对较少, Bottasso等[21]基于最优控制理论针对部分ADS-33任务单元进行了仿真分析。严旭飞和陈仁良[22]应用最优控制理论进行了倾转旋翼机倾转过渡过程的操纵策略优化分析。
本文基于最优控制方法针对倾转旋翼机近地面跃障飞行进行数值仿真研究。以倾转旋翼机纵向飞行动力学模型为基础, 考虑近地面飞行时地面效应的影响以满足低空飞行分析需求; 通过对跃障机动飞行的解析, 采用预定跃障飞行纵向位移和无预定飞行轨迹2种方式, 建立2种不同倾转旋翼机跃障飞行仿真最优控制模型; 采用直接多重打靶和序列二次规划算法进行求解。最后, 以XV-15倾转旋翼机为研究对象, 分别计算分析2种最优控制模型, 得出倾转旋翼机跃障飞行的最优动态过程。
1 倾转旋翼机纵向飞行动力学模型
倾转旋翼机具备纵向对称特征, 2台发动机以传动轴共同驱动两副旋翼; 另外不考虑横向运动, 倾转旋翼机的飞行及操纵都应当在纵向平面内; 因此建立倾转旋翼机纵向刚体动力学模型
式中:旋翼个数Nr=2;u和w分别为体轴系中纵向速度和垂向速度; q为俯仰角速度; θ为俯仰角; x为水平位移; h为高度; Iy为倾转旋翼机俯仰惯性距; FxR, FzR和MyR分别为旋翼纵向、垂向的力和俯仰力矩; Ff, FW, FHT, FVT和Mf, MW, MHT, MVT为机身、机翼、平尾、垂尾的气动力和力距; m为倾转旋翼机总重, g为重力加速度。
旋翼气动力的计算采用叶素理论、均匀入流模型、准定常一阶挥舞运动;
倾转旋翼机近地面飞行时, 性能受地效影响, 地面效应对旋翼拉力的影响因子可用(2)式表示:
式中:z是旋翼距离地面高度; R为旋翼半径; σ旋翼实度; Cla为桨叶升力线斜率; CT旋翼拉力系数, λ为旋翼入流, μ为前进比。
考虑旋翼尾迹对机翼的干扰, 将机翼划分为2个区域, 滑流区(受旋翼尾流直接影响)和自由流区(不受旋翼尾流直接影响), 自由流区的机翼气动模型和常规飞机机翼类似, 滑流区的机翼气动力模型需要考虑旋翼在机翼处的诱导速度和滑流区的面积, 如图 1所示。
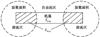 |
图1 旋翼尾流对机翼的干扰 |
机翼滑流区面积受倾转旋翼机前飞速度、短舱倾角影响,精确计算很复杂, 采用简化公式近似估计
式中:Swss为滑流区面积, Sw为机翼面积, Swfs为自由流区面积,
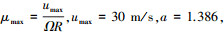 b=3.114, ηss=0.75。
b=3.114, ηss=0.75。
不考虑旋翼尾迹、机体对尾翼的气动干扰。各部件的气动力和力矩系数来自于XV-15的吹风数据[23]。
由于倾转旋翼机的操纵特点, 引入混合操纵模式, 混合操纵可将倾转旋翼机的操纵量缩减至3个, 由总距杆量δC、纵向杆δL和短舱倾转角δN表述左、右旋翼桨根总距θ0、纵向周期变距θs和升降舵偏转角θe, 方程如下
式中:δC为总距杆量、δL纵向杆量、δN短舱倾转角; δC0为总距杆零位; ∂θ0/∂δC为总距系数, 与δN相关; θ0G为总距管理器补偿量; δL0为纵向杆零位, ∂θs/∂δL为旋翼纵向周期变距系数, 与δN相关; δB1为补偿量; ∂δe/∂δL为升降舵偏转系数, 与δN相关[23]; 旋翼总距补偿角θ0L与δN相关
左右旋翼横向周期变距, θc=0为避免数值优化计算过程中的“bang-bang”现象, 采用操纵量的一阶导数作为控制变量[20]。
倾转旋翼机纵向飞行动力学方程可写为如下形式
式中:y=[u, w, q, θ, x, h, δC, δL, δN]为状态变量矩阵,
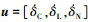 为控制变量矩阵。t为时间,
为控制变量矩阵。t为时间,
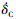 为总距杆操纵速率,
为总距杆操纵速率,
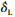 为纵向杆操纵速率,
为纵向杆操纵速率,
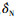 短舱倾转角速率。
短舱倾转角速率。
2 跃障飞行最优控制模型及解算方法
倾转旋翼机在敌方区域内的执行近地面飞行, 飞行高度为20 m, 以30 m/s速度前飞时, 在倾转旋翼机前方出现不太高的障碍物, 驾驶员需操纵倾转旋翼机跃过前方障碍物, 并尽可能快速回到初始高度, 以减小暴露时间; 整个机动过程由激烈的拉起和俯冲构成, 如图 2所示。直升机的跃障机动飞行并非ADS-33中的标准任务单元, 但该飞行仍然是逆仿真研究的经典动作之一[24]。
 |
图2 倾转旋翼机跃障飞行示意图 |
倾转旋翼机以直升机模式稳定前飞, 初始飞行高度为h0=20 m, 飞行速度V0=30 m/s, 进行跃升飞行, 最小跃升高度为Δhmax=30 m, 跃过障碍物后迅速下降至初始高度, 并再次进入初始稳定前飞状态。
倾转旋翼机的跃障飞行(hurdle-hop)操纵确定可以认为是一种连续时间非线性动态最优控制问题; 最优控制问题由性能指标、状态方程、边界条件和路径约束构成。
2.1 预定轨迹
预定轨迹方法也可称为基于最优控制逆解方法, 需对提供的飞行轨迹或机动动作进行定义描述, 把飞行轨迹作为仿真的输入, 对给定的轨迹采用构造函数加以描述, 使旋翼机沿该轨迹机动。针对跃障机动飞行动作, 主要是在纵向平面内完成, 飞行轨迹主要变化为高度, 因此预定倾转旋翼机高度为[24]
式中:T为飞行完成时间; Δhmax=30 m 为最大高度变化值。
1) 性能指标
针对构造函数描述的预定飞行轨迹方程(7), 为促使倾转旋翼机在跃障飞行过程中, 以预定轨迹进行机动飞行。则该性能指标函数可表征为倾转旋翼机实际仿真飞行轨迹与预定轨迹之间的误差最小化; 另外在跃障飞行过程中, 驾驶员通过快速操纵以实现倾转旋翼机的状态急剧改变, 因此需考虑抑制驾驶员的高频和迅猛操纵, 以降低驾驶员的工作负荷, 性能指标定为
式中:‖·‖为矩阵的范数计算, 本文取2-范数;T0为初始时刻, T为飞行完成时间或优化末端时刻。由于预定飞行轨迹由时域函数描述, 因此末端时间T为固定值, ww为加权系数, wc为总距杆操纵速率、纵向杆操纵速率和短舱倾转角速率的加权系数矩阵; 本文中在进行跃障飞行仿真研究中, 短舱倾角的倾转过程由优化计算同步处理。
2) 状态方程
采用上述考虑地面效应修正的倾转旋翼机飞行动力学方程(6);飞行动力学方程和最优控制模型的准确性参考文献[20]。
3) 边界条件
飞行仿真的初始边界条件为倾转旋翼机直升机模式稳定飞行状态; 依据跃障飞行解析, 飞行末端边界条件如下
式中:u0, w0为初始配平状态体轴系下纵向速度和垂向速度;θ0为初始配平机体俯仰角。
4) 路径约束
在跃障飞行过程中, 由于倾转旋翼机的操纵系统及结构限制, 优化计算中需要对操纵速率、操纵杆量等进行限制; 文献[21]依据倾转旋翼机助力器速率进行限制, 本文研究中由于针对不同的飞行完成时间T进行分析, 其操纵剧烈程度不同, 因此对操纵速率限制加以放宽, 操纵杆量的范围不变
另为保证倾转旋翼机机体姿态保持在合理的范围内, 在路径约束中对机体俯仰姿态角θ和角速率q进行限制
2.2 无预定轨迹
由于无预定轨迹, 所以将倾转旋翼机跃障飞行过程中的各类限制条件或要求转化为优化约束, 从而解算出倾转旋翼机的飞行轨迹和操纵输入。
跃障飞行主要是为迅速越过障碍物, 以减少暴露时间, 实施跃障飞行应当主要以最小飞行完成时间为性能指标, 即
无预定轨迹的最优控制模型中状态方程和基础边界约束条件与预定轨迹法模型中的一致; 跃障飞行过程中有一重要要求, 即倾转旋翼机在飞行过程在某一时刻T1跃升至某一高度h(T1), 这一高度由初始飞行高度和最小跃升量构成; 该时刻处于整个飞行完成时间内, 因此需额外添加边界约束条件
式中:Δt为一常数, 可根据不同要求进行设置, 本文设置为Δt=2 s。
其基础路径约束与预定轨迹法中的一致; 倾转旋翼机最大前飞速度受旋翼前行桨叶压缩性和后行桨叶失速效应及旋翼可用功率与动力稳定性限制, 其中旋翼可用功率的限制是最基本和最重要的限制要素, 则跃障飞行过程中的功率约束为
式中,Pmax为倾转旋翼发动机额定输出功率为1 737.5 kW。
对倾转旋翼机近地面飞行需用功率进行修正
式中:ηp为需用功率损失因子;ρ为空气密度;Ω为旋翼转速, Kind为诱导功率修正因子;vi为旋翼诱导速度;Uc旋翼桨盘无量纲垂向气流速度;CD为桨叶阻力系数。
2.3 数值解法
进行数值优化计算过程中, 由于状态变量和控制变量的量纲不同及数值之间量级差别较大, 会导致数值求解误差过大。需要对最优控制模型进行无量纲缩放化处理, 其中飞行动力学方程(6)可写成如下形式
式中
式中:k1=k2=100, k3=1, k4=100, k5=0.01, Ω0为倾转旋翼机直升机模式时的旋翼额定转速, R为旋翼半径, IR为旋翼转动惯量, δCmax为总距杆最大行程, δLmax纵向杆最大行程, δNmax短舱倾角最大行程, SP为功率无量纲缩放系数。
最优控制问题的状态量和控制量众多, 约束和目标函数非常复杂, 解析法不可行, 需通过数值优化算法进行求解。常用数值方法为间接方法和直接法, 间接法并不适用于求解大规模非线性最优控制问题; 直接法通过有限维离散将最优控制问题转化为非线性规划问题进行求解, 该类方法计算效率高, 有较好适用性。采用直接多重打靶法进行离散化处理, 并建立非线性规划模型。
将最优控制模型中的时间t平均分成N-1段, 形成N个离散时间节点T0=t1 < t2 < … < tk < … < tN=T, 每一时间段为一个打靶区间, 其中第k段时间区间为:ti=[tk, tk+1]。则形成非线规划模型中的离散优化参数
式中:yk=y(tk), uk=u(tk)在第k个打靶区间, 以时间步进的方式从tk到tk+1前向积分状态方程(16), 得到
则第k个打靶区间的残差方程组
采用同样的方式计算性能指标函数(12)、边界约束和路径约束等, 即可构建非线性规划模型
将非线性最优控制问题转化为非线性规划模型后, 应用稀疏系列二次规划算法求解即可得到最优解X*, 序列二次规划算法的计算效率高、收敛快, 适用于计算大规模非线性最优化问题。
3 倾转旋翼机跃障数值仿真
本文以XV-15为研究对象, 进行近地面跃障飞行仿真分析。倾转旋翼机的质量m=5 897 kg, 襟翼/副翼配置为40°/25°, 初始短舱倾角为90°, 进入跃升的初始状态:V0=30 m/s, h0=20 m, 稳态飞行。
图 3给出了不同飞行完成时间下的倾转旋翼机跃障飞行垂向位移变化时间历程。图中倾转旋翼机的计算高度与预定高度一致。
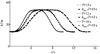 |
图3 计算和预定高度时间历程 |
图 4给出了不同飞行完成时间下的倾转旋翼机各状态量时间历程。整体而言, 不同飞行完成时间下, 各状态量及操纵策略趋势基本一致。由于完成时间不同, 导致驾驶杆的操纵速率变化激烈, 杆位移增加, 促使机体状态量快速变化。以飞行完成时间15 s为例, 其中ud, wd为地轴下倾转旋翼机前飞速度和垂向速度, 跃升初期阶段(0~4 s)基本采取提总距、前推纵向杆, 短舱前倾, 为抬头、减速、提升爬升率, 跃升中期(4~7.0 s)为调整机体俯仰角θ, 降低爬升率, 并进入保持Δhmax飞行状态; 随后低头、提升下降率进入俯冲阶段, 俯冲后期采取抬头, 减小下降率、增加前飞速度以达到初始稳态飞行。
 |
图4 预定轨迹的倾转旋翼机跃障飞行仿真 |
随着飞行完成时间的缩短, 倾转旋翼机的旋翼拉力系数CT和垂向过载Nz出现较大的波动
由于操纵及机体需在短时间内完成变化, 导致出现该类情况, 在飞行完成时间T=10 s时, 机体垂向过载最大峰值约2.0g, 最小飞行过载约0g。
同时随着完成时间的缩短, 驾驶员的操纵频率及迅猛程度在提高, 短舱倾转过程由驾驶员协调完成, 这显然会导致驾驶员工作负荷的增加。
图 5中给出了基于无预定轨迹方法的倾转旋翼机跃障飞行轨迹、操纵及机体状态量的时间历程。倾转旋翼机的操纵历程、机体状态量变化趋势与上述预定轨迹方式类似。较大不同处在于, 倾转旋翼机达到预定高度后, 并未在该高度上保持, 而是迅速下滑, 其中垂向地速wd的时间历程显示机体在爬升结束后即转入下滑过程, 缩短了跃障过程的时间, 因此相对T=10 s预定轨迹的爬升率和下降率变化相对缓和。基于最优控制方法的跃障飞行, 全局考虑倾转旋翼机的飞行轨迹、状态量和操纵历程, 以使倾转旋翼机满足目标函数(12)和路径约束的需求。其有效缩短了跃障飞行的飞行完成时间, 各状态量变化过程相对平滑, 其机体过载和旋翼拉力的变化剧烈程度小于预定轨迹方式。
 |
图5 无预定轨迹倾转旋翼机跃障飞行仿真 |
图 6给出了4种跃障飞行过程中的倾转旋翼机需用功率Pr曲线, 从图中可以看出, 预定轨迹方式随着飞行完成时间T的减小, 倾转旋翼机的需用功率的峰值在增加, 甚至超出倾转旋翼机发动机的输出功率Pmax, 如需进一步考虑功率限制, 则XV-15倾转旋翼机完成跃障飞行需至少12 s。
 |
图6 倾转旋翼机跃障需用功率时间历程 |
基于预定轨迹, 其构造函数对倾转旋翼机跃障飞行过程的合理性极其关键, 关系到倾转旋翼机机动飞行时操纵策略的实施及性能的考量; 基于无预定轨迹, 采用最优控制理论进行数值仿真, 则XV-15倾转旋翼机完成该飞行可在10 s内完成, 且各状态并未出现不合理的地方。预定轨迹的优势在于不需针对机动过程进行充分解析和制定约束, 只需建立主要变化量的构造函数; 无预定轨迹则需对机动过程充分解析以制定详细且合理的约束。
4 结论
本文针对倾转旋翼机近地面跃障飞行进行数值仿真, 采用2种建模方式, 构建跃障飞行最优控制模型, 针对本文要求的跃障飞行要求, 进行数值仿真, 得出最优化飞行轨迹和操纵, 结论如下:
1) 基于最优控制理论的逆解方法, 针对预定飞行轨迹, 可有效进行倾转旋翼机的跃障飞行仿真, 综合倾转旋翼机的各状态量限制可知, XV-15倾转旋翼机需12 s以上时间完成跃障飞行;
2) 基于无预定轨迹的最优控制模型的跃障飞行, 综合考虑跃障飞行过程中的各类约束和限制条件, XV-15倾转旋翼机可在10 s内完成机动飞行;
3) 基于最优控制理论的逆解法针对特定机动飞行, 需建立主要变化量的构造函数, 非主要变化量可放宽处理, 较适用于机动仿真的初步研究; 无预定轨迹的最优控制模型需对机动过程充分研究, 制定约束条件的合理性是影响机动仿真分析的关键, 该方法能够综合倾转旋翼机各限制条件和约束, 可最大限度的评价倾转旋翼机的能力。
References
- Wu Ximing. Current Status, Development Trend and Countermeasure for High Speed Rotorcraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47 (2): 173– 179 (in Chinese) [Google Scholar]
- Li Pan, Chen Renliang. Formulation and Validation of a Helicopter Model for Pull-up Maneuver Simulation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31 (12): 2315– 2323 (in Chinese) [Google Scholar]
- Yeo Hyeonsoo. Investigation of Rotor Airloads and Structural Loads in Maneuvering Flight[C]//64th American Helicopter Society, 2008 [Google Scholar]
- Mettler B F, Tischler M. Attitude Control Optimization for a Small-Scale Unmanned Helicopter[J]. Journal of Guidance, Control and Dynamics, 2000, 29 (2): 289– 302 [Google Scholar]
- Gadewadikar J, Lewis F A. Structured H-Infinity Command and Control-Loop Design for Unmanned Helicopters[J]. Journal of Guidance, Control and Dynamics, 2008, 31 (4): 1093– 1102 [CrossRef] [Google Scholar]
- Lee Chitai, Tsai Chingchih. Improved Nonlinear Trajectory Tracking Using RBFNN for a Robotic Helicopter[J]. Intaitonal Journal of Robust and Nonlinear Control, 2010, 20 (10): 1079– 1096 [CrossRef] [Google Scholar]
- Zhou Hongbo, Pei Hailong. Trajectory Tracking Control of Unmanned Helicopter via Filtering Backstepping[J]. Control and Decision, 2012, 27 (4): 613– 617 (in Chinese) [Google Scholar]
- Thomson D G, Bradley R. An Investigation of the Stability of Flight Path Constrained Helicopter Maneuvers by Inverse Simulation[C]//13th European Rotorcraft Forum, 1987: 122–142 [Google Scholar]
- Whalley M S. Development an Evalution of an Inverse Solution Technique for Studying Helicopter Maneuverability an Agility[J]. USAASCOM TR 90-A-008, 1991 [Google Scholar]
- Hess R A, Gao. Generalized Technique for Inverse Simulation Applied to Aircraft Maneuvers[J]. Journal of Guidance, Control and Dynamics, 1991, 14 (5): 920– 926 [CrossRef] [Google Scholar]
- Wang Zhengzhong, Zhang Xuejun, Xu Ningxin. Inverse Simulation for Helicopter Maneuver Flight and Application[J]. Helicopter Technique, 2010, 165 (4): 1– 7 (in Chinese) [Google Scholar]
- Baskett B J. Aeronautical Design standard-Handling Qualities Requirements for Military Rotorcraft[S]. Rept ADS-33E-PRF, 2000 [Google Scholar]
- Lee S, Kim Y. Time Domain Finite Element Method for Inverse Problem of Aircraft Maneuvers[J]. Journal of Guidance, Control and Dynamics, 1997, 20 (1): 97– 103 [CrossRef] [Google Scholar]
- Celi Roberto. Optimization-Based Inverse Simulation of a Helicopter Slalom Maneuver[C]//20th European Rotorcraft Forum, 2000 [Google Scholar]
- Celi Roberto. Analytical Simulation of ADS-33 Mission Task Elements[C]//American Helicopter Society 63rd Annual Forum, 2007 [Google Scholar]
- Li Jianbo, Gao Zheng. Mathematical Modeling an Its Application for Helicopter Maneuver Flight Based on Inverse Simulation[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2003, 35 (1): 1– 5 (in Chinese) [Google Scholar]
- Yang Chao, Xiong Liangyu, Zhang Xiaogu. Inverse Simulation for Helicopter Maneuvering Flight[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26 (6): 697– 700 (in Chinese) [Google Scholar]
- Ali A J. Optimal Flight of A Helicopter in Engine Failure[D]. Minneapolis University of Minnesota, 1999 [Google Scholar]
- Meng Wanli. Study and Application of Trajectory Optimization for Helicopter Flight after One Engine Failure[D]. Nanjing: Nanjing university of Aeronautics and Astronautics, 2014 (in Chinese) [Google Scholar]
- Chen Jinhe, Wang Zhengzhong, Ma Yujie. Research on Low-Speed Avoidance Zone of Tiltrotor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45 (11): 2184– 2192 (in Chinese) [Google Scholar]
- Bottasso C L, Scorcelletti F. Trajectory Optimization Strategies for the Simulation of the ADS-33 Mission Task Elements[C]//28th Eropean Rotorcraft Forum, 2008 [Google Scholar]
- Yan Xufei, Chen Renliang. Control Strategy Optimization of Dynamic Conversion Procedure of Tilt-Rotor Aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38 (7): 54– 64 (in Chinese) [Google Scholar]
- Ferguson S W. A Mathematical Model For Real Time Flight Simulation Of A Generic Tilt Rotor Aircraft[R]. NASA CR166536, 1988 [Google Scholar]
- Giulio Avanzini. Guido de Matteis Modeling Issues in Helicopter Inverse Simulation[C]//30th European Rotorcraft Forum, 2010 [Google Scholar]
All Figures
 |
图1 旋翼尾流对机翼的干扰 |
| In the text | |
 |
图2 倾转旋翼机跃障飞行示意图 |
| In the text | |
 |
图3 计算和预定高度时间历程 |
| In the text | |
 |
图4 预定轨迹的倾转旋翼机跃障飞行仿真 |
| In the text | |
 |
图5 无预定轨迹倾转旋翼机跃障飞行仿真 |
| In the text | |
 |
图6 倾转旋翼机跃障需用功率时间历程 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


