| Issue |
JNWPU
Volume 41, Number 1, February 2023
|
|
|---|---|---|
| Page(s) | 1 - 10 | |
| DOI | https://doi.org/10.1051/jnwpu/20234110001 | |
| Published online | 02 June 2023 | |
Trajectory tracking control of tilt-propulsion UAV vertical take-off and landing mode based on NLESO
基于NLESO的倾转动力无人机垂直起降模态轨迹跟踪控制
School of Aeronautics, Northwestern Polytechnic University, Xi'an 710072, China
Received:
23
April
2022
Aiming at the vertical take-off and landing mode of tilt-propulsion UAV with uncertainties such as external environment disturbance and internal parameter perturbation, this paper studies the trajectory tracking control, and proposes an internal and external double loop sliding mode control scheme based on nonlinear extended state observer (NLESO). Firstly, according to the characteristics of tilt-propulsion UAV, the dynamic model of propulsion system, aerodynamic model of fuselage/wing and yaw rudder, and dynamic equation are established in turn to complete the dynamic modeling work. Then, the internal and external uncertainties are regarded as lumped disturbances, and NLESO is designed to estimate them and compensate the control system. Afterwards, based on NLESO and sliding mode control method, the position and attitude double loop controller of VTOL mode is designed. Finally, the Lyapunov function is designed to analyze the stability of NLESO and the whole control system. Simulation results show that the proposed method significantly improves the trajectory tracking response speed and the ability to suppress uncertainties of vertical take-off and landing mode of tilt dynamic UAV.
摘要
针对存在复杂不确定性的倾转动力无人机垂直起降模态, 进行轨迹跟踪控制研究, 提出了一种基于非线性扩张状态观测器(NLESO)的内外双环滑模控制方案。基于倾转动力无人机特点, 依次建立其动力系统模型、机体与操纵舵面空气动力模型以及动力学方程, 完成动力学建模工作; 将各种内外部扰动视作集总干扰, 设计NLESO对其进行估计与补偿; 基于NLESO与滑模控制方法设计了垂直起降模态的位置与姿态双环控制器; 设计Lyapunov函数对NLESO以及整个控制系统进行了稳定性分析。仿真实验表明, 文中所提出方法针对复杂扰动具有较强的抑制能力, 显著提升了倾转动力无人机垂直起降模态的轨迹跟踪精度与响应速度。
Key words: tilt-propulsion UAV / vertical take-off and landing mode / extended state observer / sliding mode control / stability analysis / trajectory tracking control
关键字 : 倾转动力无人机 / 垂直起降模态 / 扩张状态观测器 / 滑模控制 / 稳定性分析 / 轨迹跟踪控制
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
倾转动力无人机兼具直升机与固定翼飞机的优点,具备起降灵活的特点同时可以满足更高的航程航时指标。在近几十年来,尤其是近年随着垂直起降飞行器发展热潮来临,倾转动力无人机得到了越来越多的关注[1-2]。按照结构特点划分,此类无人机大体上可以分为倾转旋翼式、倾转机翼式以及倾转涵道式这三大类[3-5],它们均是通过倾转推力矢量方向实现飞行模态的切换,具有3种飞行模态, 分别为:垂直起降模态、过渡模态与固定翼模态。本文研究重点聚焦于倾转动力无人机垂直起降模态的高精度轨迹跟踪控制。一方面,倾转动力无人机相比于多旋翼无人机结构与气动外形更为复杂,使建模误差增大,且其更大的机体参考面积导致气动扰动大,动力装置与机身之间存在气动干扰,因此其在垂直起降模态比普通多旋翼无人机需要更强的应对不确定性的能力。另一方面,为了实现倾转动力无人机在垂直起降模态的定点起降(如复杂地形或舰上),以及为过渡模态提供预设初始位置,它必须具备高精度的轨迹跟踪能力。因此,如何实现复杂不确定性情况下倾转动力无人机垂直起降模态的高精度轨迹跟踪,是一个具有理论意义与现实价值的研究问题。
目前,已有众多学者针对倾转动力无人机垂直起降模态及相关无人机面临的轨迹跟踪控制问题,提出了许多控制方法。许景辉等[6]设计了串级PID控制器,基于STM32系列微控器实现倾转三旋翼无人机的悬停状态控制。针对载荷变化对控制精度的影响,Moonumca等[7]结合PID算法与自适应算法提出了一种新型的轨迹跟踪控制方案, 仿真结果表明该方案显著增强了控制系统的鲁棒性。PID方法在现有无人机控制系统设计中依旧应用最为广泛,该方法不依赖模型且参数易于整定,但是抗干扰性和鲁棒性并不理想。滑模控制是飞行控制中应用较多的一种控制方法,对不确定性具有较好的鲁棒性。针对存在阵风干扰及未建模特性的四旋翼飞行器轨迹跟踪控制问题,丁力等[8]设计了一种位姿双环积分滑模控制器。针对受多源干扰影响的四旋翼无人机轨迹跟踪控制问题,赵振华等[9]提出了一种全回路复合快速非奇异终端滑模轨迹跟踪控制方案,显著提升了无人机轨迹跟踪的抗干扰性能。刘金琨团队关于垂直起降飞行器与四旋翼使用滑模控制方法开展了诸多研究[10-11]。
主动抗干扰方案能够通过对不确定性的估计与补偿实现干扰的快速抑制, 近年来在无人机控制设计中备受青睐[12]。扩张状态观测器(ESO)作为一种有效的抗干扰方案,将系统未建模动力学及外部扰动等视为扩张状态,通过估计扩张状态对控制器进行实时补偿[13],近年来在工程上已有所应用[14]。
1 倾转动力无人机系统模型
1.1 分系统动力学建模
本文案例倾转动力无人机由多组动力复合驱动,包括前置螺旋桨与后置分布式涵道螺旋桨,其可以在前置螺旋桨与气动操纵舵面(偏航舵面和升降副翼)的配合下,经由分布式涵道螺旋桨的倾转实现垂直起降模态与固定翼模态之间的模态转换。
采用分体建模方法,针对倾转动力无人机各分系统分别建立动力模型与气动力模型。
前置螺旋桨如图2所示,参考文献[15]根据叶素动量理论,前置螺旋桨拉力系数计算公式为
式中
式中:p, k, b, ϕr, Δϕ, R分别表示螺旋桨桨叶数, 桨叶升力线斜率、弦长、参考扭转角、总扭转角、半径;μx, μz, 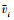 表示无量纲化的前置螺旋桨坐标系下的X向与Z向速度, 以及入流诱导速度。
表示无量纲化的前置螺旋桨坐标系下的X向与Z向速度, 以及入流诱导速度。
因此, 单个前置螺旋桨的拉力计算公式为
式中,Ω表示螺旋桨转速, A表示桨盘面积。
分布式涵道螺旋桨如图3所示, 涵道螺旋桨动力模型与孤立螺旋桨类似, 但是外部涵道会对其动力特性产生影响。涵道拉力因子被定义为外部涵道产生的拉力与系统总拉力之比
式中,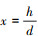 为涵道高度h与涵道内径d之比, 根据经验公式, f(x)具体表达式为:
为涵道高度h与涵道内径d之比, 根据经验公式, f(x)具体表达式为:
当0 < x≤0.2时
当0.2 < x≤1时
则一组分布式涵道螺旋桨的拉力计算公式为
式中, N为涵道螺旋桨个数。
涵道螺旋桨两两之间转向相反, 因此本文忽略它们的反扭矩以及陀螺力矩。
倾转动力无人机推进系统模型汇总为
式中:Tpl, Tpr, Tdl, Tdr分别表示左右前置螺旋桨拉力以及左右分布式涵道螺旋桨组拉力;lp, ld分别表示前置螺旋桨桨毂与涵道螺旋桨中心距机身中轴线的Y向距离;sp, sd则分别表示两者距无人机重心的X向距离。
偏航舵面操纵效果受涵道螺旋桨推力与舵面操纵量影响, 因此建立偏航舵面操纵简化气动力模型
式中: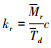 为无量纲化力矩系数;
为无量纲化力矩系数;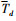 为分布式涵道螺旋桨最大推力,
为分布式涵道螺旋桨最大推力, 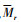 为最大偏航力矩;c为机体参考弦长;δr∈[-1, 1]为正则化后舵面操纵量。
为最大偏航力矩;c为机体参考弦长;δr∈[-1, 1]为正则化后舵面操纵量。
垂直起降模态下倾转动力无人机飞行速度较低, 其受气流影响所产生的主要为气动阻力, 因此将无人机气动力模型近似描述为
式中取k1=-0.03, k2=-0.03, k3=-0.15。
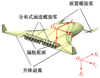 |
图1 案例倾转动力无人机简化模型 |
 |
图2 前置螺旋桨 |
 |
图3 分布式涵道螺旋桨 |
1.2 无人机动力学方程
定义惯性坐标系I与机体坐标系B。基于Newton-Euler方法, 建立倾转动力无人机垂直起降模态动力学方程为
式中: m为无人机质量;J为全机转动惯量; P =[X Y -H]T;Θ =[φ θ ψ]T;F=RIBFsum, M=RIB Msum+ Mrudder;d F, d M表示模型中的不确定性, 包括模型参数摄动, 建模误差以及外界环境干扰。
由惯性坐标系下无人机平动与转动动力学方程(9)可以看出, 针对模型中的不确定性若能得到较为准确的补偿可以使模型具备更高的精度。
2 控制系统设计
2.1 姿态指令解算
对于本文倾转动力无人机而言, 垂直起降模态下是欠驱动的, 无法在6个自由度上同时进行指令跟踪, 所以选择一个合理的控制目标方案为: 跟踪位置P与偏航角ψd, 同时保证另外2个欧拉角稳定有界, 因此θd, φd只是作为中间指令信号由虚拟控制输入生成, 用于跟踪参考位置信号。
变换方程可得
解得
针对中间指令信号θd, φd还需求得它们的一阶和二阶导数, 本文采用有限时间收敛三阶微分器实现[16]。
2.2 观测器设计
2.2.1 线性扩张状态观测器(LESO)
韩京清研究员[13]最早提出的ESO具有非线性结构, 理论分析较为困难, 因此早期研究进展较为缓慢。随着高志强教授等人提出了线性自抗扰控制器[17], 将原本的非线性结构线性化、简洁化, 使ESO应用更为广泛。
以无人机外环为例, 可以基于位置误差设计二阶线性观测器。线性扩张状态观测器设计为
观测误差方程定义为e=[e1 e2 e3]T, 得
则观测误差状态方程写为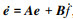 , 通过选择, 使A为Hurwitz矩阵, 可实现误差的有效跟踪, 关于线性扩张状态观测器的稳定性证明见文献[18]。
, 通过选择, 使A为Hurwitz矩阵, 可实现误差的有效跟踪, 关于线性扩张状态观测器的稳定性证明见文献[18]。
2.2.2 非线性扩张状态观测器(NLESO)
在普通低成本无人机中, 速度(地速)测量可以达到较为良好的精度。另外, 由于LESO随着观测误差减小收敛速度降低, 对于时变扰动不利于快速收敛至精准误差边界之内。因此本节设计了一种改进的非线性扩张状态观测器, 其计算复杂度与LESO相近, 但可以依据误差尺度进行自适应调整, 实现更加快速精准的观测。
存在系统
设计非线性扩张状态观测器(NLESO)
设计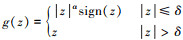 , 其中ε>0, 0 < α < 1, 0 < δ≤1。
, 其中ε>0, 0 < α < 1, 0 < δ≤1。
定义
误差方程为
式中, 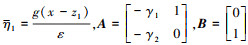 , 通过选择γ1, γ2使A为Hurwitz矩阵。
, 通过选择γ1, γ2使A为Hurwitz矩阵。
定理1 对于非线性系统(9)和非线性扩张状态观测器(17), 存在参数k1, k2, k3, k4, γ1, γ2, 使误差估计收敛至原点的一个小邻域内。
证明 针对本文所设计非线性扩张状态观测器进行稳定性分析时, 构建其Lyapunov方程为
各项参数需满足以下条件
P为正定对称矩阵, 存在正定对称矩阵Q满足AT P + PA =- Q。
根据|z|≤δ与|z| >δ, 分别进行观测器稳定性分析。
情况1 |z|≤δ
观测器收敛条件为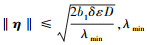 为Q的最小特征值, b1=max(k3, k4), 其收敛速度取决于ε, ε越小收敛速度越快。
为Q的最小特征值, b1=max(k3, k4), 其收敛速度取决于ε, ε越小收敛速度越快。
情况2 | z| >δ
观测器收敛条件为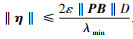 , 其收敛速度取决于ε, ε越小收敛速度越快。
, 其收敛速度取决于ε, ε越小收敛速度越快。
2.3 轨迹跟踪控制方案
本文倾转动力无人机在垂直起降模态下, 采用内外环的双层控制结构, 基于滑模控制方法增强系统鲁棒性, 使用NLESO对外界复合干扰进行实时观测与补偿。
2.3.1 位置子系统控制器设计
位置子系统动力学模型为
位置子系统控制器的设计, 需要实现存在不确定性情况下的高精度轨迹跟踪, 则定义位置跟踪误差为ep= P - Pd。滑模面设计为
直接力控制输入设计如下
而基于扩张状态观测器的控制器设计为
式中:λ1>0, c1>0为待设计参数;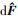 表示d F的观测器估计值。
表示d F的观测器估计值。
2.3.2 姿态子系统控制器设计
通过内环控制律的设计实现姿态跟踪, 为了有效跟踪姿态信号, 需要设计输入力矩M。姿态子系统模型简化为
式中,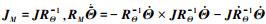 , 定义姿态误差为eΘ= Θ - Θd。滑模面设计为
, 定义姿态误差为eΘ= Θ - Θd。滑模面设计为
力矩控制输入设计为
其中使用饱和函数sat(s2)代替sign(s2)减缓切换抖振, λ2>0, c2>0为待设计参数。
2.4 操纵变量控制分配
本文所提出的基于NLESO与双环滑模控制器的控制结构如图4所示。
根据位置环与姿态环虚拟控制量F和M, 可以反向解算出控制系统所需的力与力矩, 通过控制分配将力与力矩分配至各执行机构
式中, Tpl, Tpr, Tdl, Tdr, lp, ld, sp, sd已经在(6)式进行了定义, Myaw表示偏航舵面力矩。
进一步由(3), (5), (7)式可以解算出推进系统各螺旋桨转速与偏航舵面操纵量。
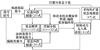 |
图4 控制系统结构图示 |
3 控制系统稳定性分析
综合考虑观测器和控制器构成的闭环系统, 外环Lyapunov函数为
其中相关参数还需满足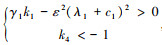 , V1, V2分别为外环控制器与观测器Lyapunov函数。
, V1, V2分别为外环控制器与观测器Lyapunov函数。
由非线性扩张状态观测器误差方程式(19)可得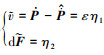 , 从而建立起观测器误差矩阵与控制系统误差变量间映射关系。
, 从而建立起观测器误差矩阵与控制系统误差变量间映射关系。
定理2 对于闭环系统(9)式与扩张状态观测器(17)式以及控制器(25)式, 存在设计参数λ1, γ1, γ2, ε, 使得误差收敛到原点附近小邻域。
证明 针对外环控制器, 由(25)式可得基于扩张状态观测器的控制器。外环Lyapunov函数为
式中, 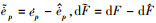 , 分别表示各自真值与估计值的差值。
, 分别表示各自真值与估计值的差值。
存在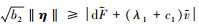 , 其中
, 其中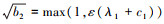 , 则
, 则
针对|z|≤δ与|z|>δ, 分为2种情况进行完整系统稳定性分析。
情况1 |z|≤δ
式中
可以解得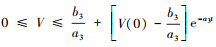 , 而
, 而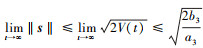 , 通过增大a3以及减小ε, 可使s收敛于零点足够小邻域。
, 通过增大a3以及减小ε, 可使s收敛于零点足够小邻域。
情况2 |z| >δ
令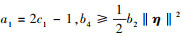 , 则
, 则
进一步可以解得
故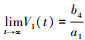 , 其收敛速度取决于控制增益c1与观测误差。
, 其收敛速度取决于控制增益c1与观测误差。
综合考虑观测器和控制器构成的闭环系统, 通过取充分大的c1与足够小ε, 可使函数收敛。
4 仿真实验
本文案例倾转动力无人机主要参数为总质量m为18 kg, 转动惯量I=diag(0.87, 1.1, 1.55), 全机参考面积S=1.15 m2, 参考弦长c=0.6 m。
设置无人机初始条件为
针对倾转动力无人机系统设计非线性扩张状态观测器参数为α=0.5, δ=0.1, ε=0.02, 取γ1=3, γ2=2, 则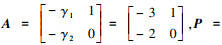
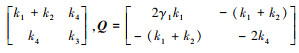 。
。
令k2=1, 得k1=1, 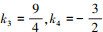 。
。
位置子系统控制器参数为: λ1=diag(6, 6, 6), c1=4, 姿态子系统控制器参数为λ1=diag(30, 30, 30), c1=6, η=0.2。
本文在双环滑模控制器的基础上, 设计使用不同的扰动估计/观测算法, 共同组成控制系统, 将仿真控制系统分为4种, 分别为: 滑模控制器、滑模控制器+自适应扰动估计器(adaptive disturbance estimator)、滑模控制器+线性扩张状态观测器、滑模控制器+非线性扩张状态观测器, 并且针对不确定性开展仿真实验。
倾转动力无人机垂直起降模态所面临的不确定性主要来源于环境扰动, 具体体现为复杂风场引起的外力干扰。因此, 将不确定性设置如下
为了使仿真飞行场景更加合理, 根据垂直起降模态外场飞行实验设计飞行轨迹。由于垂直起降模态下, 无人机主要执行垂直起飞、垂直降落, 以及为过渡飞行做准备的位置调整(水平位移)与方向调整(定点调姿)。因此, 设计期望轨迹为从原点O垂直上升至A点(0~4 s), 然后向前平移至B点(4~6 s), 在B点悬停并左转90°(6~10 s), 再平移至C点(10~12 s), 最后垂直降落至D点(12~16 s与16~18 s)。
由图5a)可知,4种控制系统均实现了对于三维轨迹的基本跟踪效果,但是结合LESO与NLESO的控制系统跟踪效果明显更好,在垂直起飞与垂直降落中基本无“漂移”现象,并且在定点调姿中也稳定地保持在预定位置。进一步,根据图5b)图进行定量误差分析。由于期望指令的瞬时性与控制器响应时间之间的差异,不可避免地存在过程误差,但是4种控制系统均较快地消除了跟踪误差。单独SMC与结合自适应扰动观测器的SMC跟踪误差更大,在定点调姿中(6~10 s),它们持续抖动的轨迹跟踪误差更为明显。
得益于本文所设计控制器具有合理控制分配与姿态指令实时解算能力,4组控制器在姿态指令跟踪中均拥有响应快、收敛准的优良表现。
在扰动的直接观测方面,图7a)直观地展现了不同扰动估计器/观测器的扰动观测效果。自适应扰动估计器存在较大的迟滞,无法实现对时变扰动的精准估计,因此虽然其具有一定的扰动观测能力,但是所产生的最终控制效果依然不够理想。相比之下,LESO与NLESO的优良扰动观测能力得到凸显,两者均实现了对三向力扰动的实时准确观测。为了对比LESO与NLESO的优劣,图7b)进一步在精确范围内展现了两者的观测误差。NLESO在与LESO具有相近计算复杂度的基础上,具有更精准的扰动观测能力,对时变扰动的观测始终保持在一个很小的误差范围之内,其性能相比于LESO提升了一倍多。
图8展示了各控制器的操纵变量响应曲线。单独SMC与结合自适应扰动估计器的SMC操纵响应存在明显抖动,而SMC+LESO也出现很多脉冲式操纵响应。基于NLESO快速、精准的扰动观测能力,SMC+NLESO控制器操纵变量响应平滑性最佳,推进系统各螺旋桨转速连续变化且始终工作在合理转速范围。
 |
图5 位置指令跟踪曲线 |
 |
图6 姿态指令跟踪曲线 |
 |
图7 观测器扰动观测曲线 |
 |
图8 操纵变量响应曲线 |
5 结论
本文针对倾转动力无人机垂直起降模态存在复杂不确定性情况,开展轨迹跟踪控制研究。首先,针对倾转动力无人机的特点,基于分体动力学建模方法建立了可靠的无人机系统模型;然后,针对系统不确定性设计NLESO进行实时估计与补偿;接下来基于NLESO与内外双环结构的滑模控制器,完成了轨迹跟踪控制方案的设计,并且通过控制分配解算出操纵变量;最后设计了Lyapunov函数,完成了NLESO以及整个控制系统的稳定性分析。
通过仿真实验,NLESO相较于LESO及自适应扰动估计器体现出更优的扰动观测能力,其响应精度与速度均具有明显的优势。同时,验证了所设计控制系统对于复杂不确定性的强抑制能力,倾转动力无人机在垂直起降模态能够实现快速、准确的轨迹跟踪,验证了本文所提出方法的有效性与优越性。
References
- WANG Z, ZHENG G, CHENG Y, et al. Practical control implementation of tri-tilt rotor flying wing unmanned aerial vehicles based upon active disturbance rejection control[J]. Journal of Aerospace Engineering, 2020, 234(4): 943–960 [Google Scholar]
- XIA J Y, ZHOU Z. Model predictor control based on ILQR for Tilt-propulsion UAV[J]. Aerospace, 2022, 33(1): 282–295 [Google Scholar]
- LIU N J, CAI Z H, ZHAO J, et al. Predictor-based model reference adaptive roll and yaw control of a quad-tiltrotor UAV[J]. Chinese Journal of Aeronautics, 2020, 33(1): 282–295 [Article] [Google Scholar]
- MURAOKA K, OKADA N, KUBO D. Quad tilt wing VTOL UAV: aerodynamic characteristics and proto type flight[C]//AIAA Infotech@Aerospace Conference, Seattle, Washington, 2009 [Google Scholar]
- ZHAO Changhui, DUAN Hongwei, ZHANG Anping. Agusta project zero new vertical take-off and landing technology verification machine[C]//2014(5th) China UAV Conference, Beijing, 2014 (in Chinese) [Google Scholar]
- XU Jinghui, MA He, ZHOU Jianfeng, et al. Hovering attitude control of tilt three rotor vertical takeoff and landing UAV[J]. Journal of Agricultura Machinery, 2018, 49(10): 16–22 [Article] (in Chinese) [Google Scholar]
- MOONUMCA P, YAMAMOTO Y, DEPAIWA N. Adaptive PID for controlling a quadrotor in a virtual outdoor scenario: simulation study[C]//2013 IEEE International Conference on Mechatronics and Automation, 2013 [Google Scholar]
- DING Li, RUAN Wenrui, CHAO Yuan, et al. Dual loop conditional integral sliding mode control for four rotor aircraft[D]. Electro Optic and Control 2022294731 [Article] (in Chinese) [Google Scholar]
- ZHAO Zhenhua, XIAO Liang, JIANG Bin, et al. Fast nonsingular terminal sliding mode trajectory tracking control of four rotor UAV based on extended state observer[D]. Control and Decision Making 202237922012210 [Article] (in Chinese) [Google Scholar]
- LIU Jinkun, GONG Haisheng. An anti-saturation sliding mode control for VTOL vehicle[D]. Journal of Electrical Machines and Control, 2013, 17(3): 92–97 (in Chinese) [Google Scholar]
- FANG Xu, LIU Jinkun. Dynamic surface control for quadrotor un-manned air vehicle[D]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1777–1784 [Article](in Chinese) [Google Scholar]
- WANG H, CHEN M. Trajectory tracking control for an indoor quadrotor UAV based on the disturbance observer[J]. Transactions of the Institute of Measurement and Control, 2016, 38(6): 675–692 [Google Scholar]
- HAN Jingqing. Auto-disturbance-rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 19–23 [Article] (in Chinese) [Google Scholar]
- CUI R, CHEN L, YANG C, et al. Extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities[J]. IEEE Trans on Industrial Electronics, 2017, 64(8): 6785–6795 [CrossRef] [Google Scholar]
- WANG X H, CAI L L. Mathematical modeling and control of a tilt-rotor aircraft[J]. Aerospace Science and Technology, 2015, 47: 473–492 [CrossRef] [Google Scholar]
- KHALIL H K. Nonlinear systems[M]. 3rd ed. Englewood Cliffs, NJ: Prentice-Hall, 2002 [Google Scholar]
- GAO Z Q. Scaling and bandwidth-parameterization based controller tuming[C]//2003 American Control Conference, NJ, USA, 2003 [Google Scholar]
- GUO B Z, ZHAO Z. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420–430 [CrossRef] [Google Scholar]
All Figures
 |
图1 案例倾转动力无人机简化模型 |
| In the text | |
 |
图2 前置螺旋桨 |
| In the text | |
 |
图3 分布式涵道螺旋桨 |
| In the text | |
 |
图4 控制系统结构图示 |
| In the text | |
 |
图5 位置指令跟踪曲线 |
| In the text | |
 |
图6 姿态指令跟踪曲线 |
| In the text | |
 |
图7 观测器扰动观测曲线 |
| In the text | |
 |
图8 操纵变量响应曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


