EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 37 / No 1 (February 2019) JNWPU, 37 1 (2019) 7-12 Full HTML
Open Access
Issue
JNWPU
Volume 37, Number 1, February 2019
Page(s) 7 - 12
DOI https://doi.org/10.1051/jnwpu/20193710007
Published online 03 April 2019

© 2019 Journal of Northwestern Polytechnical University

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

由于相关技术的飞速发展, 太阳能无人机的续航时间不断增加, 太阳能无人机逐渐迈入实用化阶段。以“探路者[1]”和“太阳神[2]”为代表的全翼布局是太阳能无人机的一种重要布局形式, 与常规布局的太阳能无人机相比, 其具有结构简洁、气动效率高、太阳能电池铺设率高等优点。

由于太阳能无人机对于重量十分敏感, 且起落架的工作时间较短, 全翼布局太阳能无人机的起落架设计必须尽可能轻量化, 通常由4个轮胎和2个碳纤维支架组成, 没有专门的减震机构和转向伺服机构, 前轮有自由转向和固支2种形式。由于没有前轮转向伺服舵机和方向舵, 全翼布局太阳能无人机只能通过螺旋桨动力差动进行滑跑过程的横航向控制。因此, 有必要对全翼布局太阳能无人机滑跑过程进行建模, 并设计采用动力差动为控制输出的滑跑控制方法。

针对无人机滑跑问题, 文献[3]建立了前三点式布局无人机包含起落架和刹车装置的数学模型, 并设计了基于主动刹车和方向舵偏转的纠偏控制律。文献[4]提出采用加权伪逆法对偏航力矩及阻力控制指令进行动态控制分配的方法。文献[5]对四轮起落架布局的无人机进行了建模, 并设计了简单的纠偏控制方法。

由于全翼布局太阳能无人机滑跑过程中速度变化范围较大, 受到气动和地面的复合作用, 同时螺旋桨动力差动效率变化范围较大, 因此所设计的滑跑控制器必须具有很好的抗干扰能力。文献[6]对非线性自抗扰控制方法进行简化, 提出了以线性扩张状态观测器(LESO)为核心的线性自抗扰控制方法(LADRC)。该方法在具有较强抗干扰能力的同时, 大大简化了参数整定过程, 具有较好的工程实现价值。本文在相关研究的基础上, 建立了全翼布局太阳能无人机滑跑模型, 并对其滑跑特性进行了分析。设计了基于线性自抗扰理论的偏航角控制器。在偏航角控制器的基础上通过改进向量场轨迹跟踪方法, 设计了适合起降过程的直线轨迹跟踪器。

1 全翼布局太阳能无人机滑跑动力学模型与滑跑特性分析

本文中研究的全翼布局太阳能无人机由中央翼段、外翼段、垂直安定面和起落架组成, 布局形式如图 1所示。

thumbnail 图1

全翼布局太阳能无人机

1.1 滑跑动力学模型

1.1.1 起落架模型

假设无人机除轮胎外都是刚体, 2种起落架结构形式下, 地面对无人机的作用力如图 2所示。图 2a)和图 2b)分别为前轮自由转向和前轮固支时的受力情况。其中FnFfFs为轮胎受到地面的支持力、摩擦力和侧向力; af和ar分别为前轮和后轮到重心的纵向距离; bt为轮胎到飞机对称面的水平距离; βs为侧偏角。

将轮胎简化为弹簧-阻尼系统, 并忽略其质量, 可以得到

式中，Kδt为轮胎的等效弹簧刚度; Cδt为轮胎的等效阻尼系数; δti和 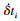是轮胎的压缩量和压缩速度。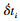可以通过δti对时间进行求导得到。通过无人机的状态和起落架几何关系得到轮胎的压缩量:

式中, H是重心到地面的距离; h为轮胎无压缩时无人机重心的离地高度; θ为俯仰角; φ为滚转角。sat为饱和函数, 将轮胎变形量限制在0~0.02 m之间。

轮胎受到的摩擦力和侧力可以表示为:

式中, μf为轮胎的滚动摩擦因数; Ks为轮胎的侧偏刚度。公式(5)只有在βsi为小角度时才成立, 通常应小于5°。

假设滑跑过程中无人机的俯仰滚转姿态为小量, 对于前轮固支的情况, 可以通过以下公式求解βsi:

式中, uv为体轴系下xy方向的速度; r为偏航角速度。对于前轮自由转向的情况:前轮会始终保持与航向平行, 故βs1=βs2=0;后轮侧偏角与固支布局的计算方法相同。

由于滑跑过程中俯仰角、滚转角和轮胎的侧偏角为小量, 故机体受到地面的作用力和力矩可以表示为:

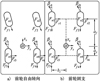thumbnail 图2

前轮自由转向和前轮固支布局起落架受力示意图

1.1.2 螺旋桨动力差动模型

螺旋桨拉力可以简化为[7]:

式中, Sp和Cp为螺旋桨的桨盘面积和拉力系数; δp是油门大小; Kp为螺旋桨出流速度与油门之间的增益; Vp为螺旋桨处的来流速度。考虑到偏航角速度的影响, Vp可以表示为

式中, Vpl和Vpr分别为左右螺旋桨处的来流速度; dp为螺旋桨到飞机对称面的距离。

定义Δδp为油门差动量, 左右油门可以表示为

螺旋桨动力差动可以表示为

螺旋桨作用到飞机的力和力矩可以表示为：

当Δδp=0时, (12)式可以简化为ΔT=-2ρSpCpdpr, 由于ρ, Sp, Cp, dp都大于0, 双螺旋机设计能够为飞机带来额外的偏航阻尼。

1.1.3 完善滑跑模型

将无人机除了轮胎以外的部分视为刚体, 忽略轮胎的重量, 通过建立刚体六自由度模型来描述无人机的运动。无人机在滑跑过程中除了受地面和螺旋桨提供的力和力矩, 还受到气动力、力矩和重力的作用。飞机基本的动力学、运动学方程和飞机气动、重力的作用方程在文献[7]中有详细介绍, 因此这里不再赘述。

1.2 滑跑特性分析

2种布局的起落架在高低2种速度下受到大小为1 N·m持续时间2 s的航向力矩干扰时的响应曲线如图 3所示。

由图 3a)和图 3b)可知在低速滑跑时, 前轮自由转向布局受到航向力矩的影响时产生的侧向偏离和偏航角远大于前轮固支的布局。由(6)式可知, 这主要是因为在速度较低时, 航向角速度r的影响较大, 前轮固支布局的前轮受到侧力的影响, 会提供一定的航向阻尼。因此, 在低速滑行时前轮自由转向的布局需要更少的控制力矩。由图 3c)和图 3d)可知在高速滑跑时, 前轮固支的布局侧向偏离反而稍大于前轮自由转向布局。这是因为在高速时偏航角速度r对侧偏角的影响很小, 轮胎提供的阻尼降低。同时受气动的影响, 无人机出现较大的滚转角, 进而左侧轮胎离地, 前轮固支布局的右前轮受到的侧力能够提供部分的航向力矩。

thumbnail 图3

2种不同布局的起落架在高低2种速度下滑跑受扰后的响应曲线

2 滑跑控制律设计

滑跑控制律主要由偏航角控制器和轨迹跟踪器组成。

2.1 偏航角控制器

基于线性自抗扰控制理论设计偏航角控制器, 具体由偏航角回路和偏航角速度回路组成, 其结构如图 4所示。

不考虑滚转角和俯仰角的影响时, 航向动力学方程可以写为严格仿射的形式

式中，fr为总和扰动, 即待观测动态环节。

设计偏航角回路的过渡过程环节(TD), 该环节能有效减少控制过程中的超调。

式中，fhan为最速控制综合函数; rψ决定跟踪速度; h0为滤波系数; ψcmd为偏航角指令; ψref为过渡指令。

设计偏航角回路的反馈环节, 由于公式(15)第一项齐次, 故使用线性反馈即可

式中，Kψ为反馈增益; m为整数使

设计偏航角速度回路的线性扩张状态观测器(LESO), 式中β01, β02为待整定参数

设计偏航角速度回路的反馈环节

式中将动力差动幅度限制为±20%。

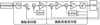thumbnail 图4

偏航角控制器结构

2.2 直线轨迹跟踪器

文献[8]提出了基于向量场的直线轨迹跟踪方法, 该方法相比于目前较为常用的L1轨迹控制器等目标点跟踪方法具有跟踪误差较小和使用范围不受距离限制等优点[12]。无人机与路径的示意图如图 5所示。

图中，ψt为跑道的方向角; d为无人机到跑道的距离。向量场轨迹跟踪方法具体的数学表达式为

式中，ψ∞∈(0, π/2]表示当d无穷大时向量场方向与跑道的夹角; Kd为距离的增益, Kd越小转弯过程越平滑; n为整数, 使得ψcmd∈[-π, π]。通过(21)式可以看出, 向量场轨迹跟踪方法适用于速度基本保持不变的情况, 不适用于起飞、降落滑跑等速度发生很大变化的情况, 因此需要对公式进行改进, 引入

式中，Kd为新的增益参数, 是一个正常数; V为无人机的速度。因此当速度增加时Kd减小, 无人机的运动轨迹变得缓和。将(22)式代入(21)式可得

thumbnail 图5

无人机与目标路径的示意图

3 仿真分析

3.1 仿真条件与控制器参数

研究所用的全翼布局太阳能无人机起飞重量15 kg, 平均气动弦长0.4 m, 翼展7 m, 螺旋桨动力差动的范围为20%, 动力系统采用时间常数为0.02 s的惯性环节代替。

偏航角控制器参数:选取rψ=0.1, h0=0.01, Kψ=1, Kr=10, β01=100, β02=300。直线轨迹跟踪器的参数:ψ∞=π/4, Kd=0.5。

3.2 偏航角控制器

图 6验证偏航角控制器在1 m/s和10 m/s的2种速度下对比前轮自由转向和前轮固支布局的控制效果。

由图 6a)和图 6b)可知, 在低速滑跑过程中, 前轮自由转向的布局能够很好地跟踪偏航角指令, 并且螺旋桨动力差动幅值较小。而前轮固支的布局由于螺旋桨动力差动饱和引起了较大的超调。因此, 前轮自由转向布局更适合于无人机需要从机库自行移动到跑道等需要较长时间低速滑跑的情况, 而前轮固支的布局则需要专门的运载工具。

由图 6c)可得, 在高速度滑跑时, 偏航角控制器具有很好的控制效果。图 6d)表明, 与低速情况相反, 高速时前轮固支布局所需要的螺旋桨动力差动幅值更小, 表明高速滑跑时前轮固支布局反而更有优势。

thumbnail 图6

2种前轮布局在不同速度下跟踪偏航角指令时, 偏航角和螺旋桨动力差动响应曲线

3.3 直线轨迹跟踪器

通过仿真起飞滑跑和降落滑跑过程中无人机对直线轨迹的跟踪能力来验证直线轨迹跟踪器对2种前轮布局的控制效果。起飞滑跑过程油门以每秒5%的速度从20%增加到80%, 当速度大于12 m/s时结束仿真。降落滑跑过程中油门始终维持在20%, 当速度小于1 m/s时结束仿真。

由图 7a)可得, 在起飞滑跑过程中2种前轮布局都能有效跟踪直线轨迹, 前轮自由转向布局的响应时间较快, 但出现了轻微的超调。由图 7b)可得, 前轮固支的布局在2~5 s时出现了控制输出饱和, 但轨迹跟踪效果没有受到很大影响。

与图 7a)相比, 图 7c)表明降落过程中的轨迹跟踪响应速度较慢, 这是由于在降落滑跑过程中, 螺旋桨动力差动的效率较低。图 7d)表明2种前轮布局形式都出现了控制器输出饱和, 但都有明显跟踪直线轨迹的趋势, 没有出现不稳定的情况。通过对比滑跑距离可以发现, 全翼布局太阳能无人机的降落滑跑距离要大于起飞滑跑。

在图 7仿真条件的基础上, 图 8将模型中所有的气动导数正向拉偏20%, 并且螺旋桨差动效率负向拉偏20%, 同时t=0时刻加入sin(2t) N·m的航向干扰力矩后进行仿真, 验证控制器的鲁棒性。

对比图 7与图 8可得, 虽然进行了气动参数拉偏、加入干扰力矩且减小了执行机构的效率, 控制器依然能有效控制2种起落架布局的无人机完成起降滑跑。表明所设计的控制方法具有较好的鲁棒性, 能够有效应对各种干扰。

thumbnail 图7

2种前轮布局在起降滑跑过程中的响应曲线
thumbnail 图8

加入参数拉偏和扰动后, 2种前轮布局在起降滑跑过程中的响应曲线

4 结论

1) 通过合理设计控制方法, 即使只采用螺旋桨动力差动, 依然能够有效对前轮自由转向布局和前轮固支布局的全翼布局太阳能无人机起降滑跑过程进行控制。

2) 在低速滑跑过程中, 与前轮固支布局相比, 前轮自由转向布局具有更好的控制效果, 无需其他运载工具就可实现自行移动, 具有更好的自持能力。在中高速滑跑过程中, 通过合理设计控制器, 2种前轮布局形式都具有很好的控制效果。

3) 论文所设计的控制方法结构简单, 鲁棒性较好, 待整定参数较少, 同时采用实际可测的物理量, 具有较好的工程实现性。

References

  1. Flittie K, Curtin B. Pathfinder Solar-Powered Aircraft Flight Performance[C]//23rd Atmospheric Flight Mechanics Conference, 1998: 4446 [Google Scholar]
  2. Seong Y B, Lim J H, Yeo M S, et al. HELIOS:Solar Rights Analysis System for Apartment Buildings[J]. Solar energy, 2006, 80(6): 723-741 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  3. Wang Yong, Wang Yingxu. Lateral Deviation Correction Control for UAV Taxiing[J]. Acta Aeronoutica et Astronautica Sinica, 2008 (suppl 1): 142-149 (in Chinese) [Article] [Google Scholar]
  4. Wang Yanxiong, Zhou Zhou, Shao Zhuang, et al. Lateral Deviation Correction Control for Flying-Wing UAV Taxiing[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 593-601 (in Chinese) [Article] [Google Scholar]
  5. Deng Yinping, Fan Yanming. Design and Simulation of Ground Taxiing System for UAV with Four Wheels[J]. Journal of System Simulation, 2008, 20(21): 5929-5935 (in Chinese) [Article] [Google Scholar]
  6. Gao Z. Scaling and Bandwidth-Parameterization Based Controller Tuning[C]//Proceedings of the American Control Conference, 2006: 4989-4996 [Google Scholar]
  7. Beard R W, Mclain T W. Small Unmanned Aircraft:Theory and Practice[M]. New Jersey, Princeton University Press, 2012: 28-59 [Google Scholar]
  8. Nelson D R, Barber D B, Mclain T W, et al. Vector Field Path Following for Miniature Air Vehicles[J]. IEEE Trans on Robotics, 2007, 23(3): 519-29 [Article] [CrossRef] [Google Scholar]
  9. Sujit P, Saripalli S, Sousa J B. Unmanned Aerial Vehicle Path Following:a Survey and Analysis of Algorithms for Fixed-Wing Unmanned Aerial Vehicless[J]. IEEE Trans on Control Systems, 2014, 34(1): 42-59 [Article] [Google Scholar]

All Figures

thumbnail 图1

全翼布局太阳能无人机
In the text
thumbnail 图2

前轮自由转向和前轮固支布局起落架受力示意图
In the text
thumbnail 图3

2种不同布局的起落架在高低2种速度下滑跑受扰后的响应曲线
In the text
thumbnail 图4

偏航角控制器结构
In the text
thumbnail 图5

无人机与目标路径的示意图
In the text
thumbnail 图6

2种前轮布局在不同速度下跟踪偏航角指令时, 偏航角和螺旋桨动力差动响应曲线
In the text
thumbnail 图7

2种前轮布局在起降滑跑过程中的响应曲线
In the text
thumbnail 图8

加入参数拉偏和扰动后, 2种前轮布局在起降滑跑过程中的响应曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.