| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 13 - 20 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710013 | |
| Published online | 03 April 2019 | |
Research of Filling Ratio and Fluidization Performance of Dense-Packing Aluminum Powder
铝粉致密装填率及其流化性能研究
1
School of Aerospace, Northwestern Polytechnical University, Xi’an 710072, China
2
Xi'an Modern Chemistry Research Institute, Xi’an 710065, China
Received:
12
March
2018
Based on the granule packing theory, grading vibrating filling experiments have been carried out for aluminum powder with different particle sizes. The effects of the several factors on the dense filling ratio of aluminum powder, such as filling craft, vibration time and grading parameter, have been discussed. The distribution uniformity of particle size and fluidization performance of the dense-packing aluminum powder have been detected and analyzed. The results show that the powder filling ratio can be improved greatly by performing the batch packing, stirring and vibrating on powder. The initial vibration can improve the powder filling ratio obviously, but the ascension is not obvious with the increasing of vibration time. The selection of grading parameter should ensure that the small particles can fill in the gaps among large particles. The filling ratio as high as 73.02% has been obtained under the grading parameter m100 μm:m15μm:m1μm=6.89:2.97:1. The testing results show that the size uniformity of aluminum powder obtained by this filling craft is good at the same height, but need to be improved at different heights. The fluidization performance of dense-packing aluminum is good, and the accuracy of powder supply reaches 3.6%, which can meet the requirement of powder supply in powder rocket engine.
摘要
以颗粒堆积理论为基础,对不同粒径的铝粉进行级配振实装填实验研究,探讨了装填工艺、振动时间和级配参数对铝粉致密装填率的影响,并对致密装填所得的铝粉粒径分布均匀性及粉末流化性进行了实验检测分析。结果表明,对粉体进行分批装填、搅拌和振动,可以极大地提高粉体装填率;初期的振动对装填率提升比较明显,随着振动时间的逐渐加长,装填率提升增益将逐渐减小;级配参数的选取应尽量保证小颗粒能填满大颗粒间形成的空隙,最终在m100 μm:m15 μm:m1 μm=6.89:2.97:1的级配参数下获得了高达73.02%的致密装填率;检测分析结果表明该装填工艺所得铝粉在同一高度处均匀性良好,不同高度处均匀性还有待改善,致密装填所得铝粉的流化性能良好,且粉末供给精度达到了3.6%,可以满足粉末火箭发动机供粉要求。
Key words: granule packing / grading vibrating filling / fluidization performance of powder / powder rocket engine
关键字 : 颗粒堆积 / 级配振实装填 / 粉末流化性 / 粉末火箭发动机
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
粉末火箭发动机使用金属粉末作为燃料, 可通过控制进入燃烧室的粉末流量来控制推力大小, 因而具有推力调节功能, 也可以通过控制阀门的开闭实现多次启动关机, 是一种具备先进的能量管理技术的火箭发动机[1-2]。粉末火箭发动机理论体积比冲很高, 但由于其使用的燃料、氧化剂均为固体粉末状, 导致其实际装填率不可能达到100%, 从而其实际体积比冲要低于理论体积比冲。因而提高粉末燃料的实际装填密度对提升粉末火箭发动机的比冲性能具有重大意义。
对于单一粒径球形颗粒的堆积, 随意松排、随意密排和规则密排是3个比较常见的颗粒堆积概念, 国外研究者们围绕这3个概念做了大量的研究[3-6]。20世纪60年代, Yerazunis等[7]对不同粒度大小的二元(尺寸)粒子堆积进行了分析与研究, 并得到了堆积密度随大、小颗粒尺寸比变化的理论分析结果, 同时也分析了大、小颗粒所占质量比对混合物堆积密度的影响。Mcgeary[8]得到了颗粒堆积密度随着大、小颗粒尺寸比的增加而增大, 当这个比值大于10之后, 二元系统堆积密度值的增加变得十分缓慢。近年来, 国外学者对于细小粉体的实际堆积问题也进行了大量的实验和数值研究。Li等[9]通过实验方法研究了干式充填法和湿式填装法对包含胶结材料、细骨料和粗骨料的混凝土混合物堆积密度的影响, 结果发现湿式填装工艺下混凝土混合物堆积密度更大, 孔隙率更小, 并且超细辅助胶结材料充填效果更好。Parteli等[10]通过实验和数值模拟相结合的手段研究了4~52 μm细玻璃粉体的堆积密度, 研究发现在数值模拟过程中若忽略颗粒间范德华力的作用, 则模拟结果将与实验结果相差甚远, 表明了实际粉体装填时, 细小颗粒间的范德华力对粉体堆积密度的影响不可忽略。
近年来, 国内也有许多学者对粉体堆积问题进行了大量的数值计算和实验研究。清华大学的吴成宝等[11]探讨了多级配规则球形粉体颗粒致密堆积密度的理论值与级配数的关系, 致密堆积状态下粒径分布特征, 以及粉体堆积密度的理论值与单一粉体颗粒干扰宽度和初始空隙率的关系。国防科技大学的欧阳鸿武等[12]研究了二元球形粉体颗粒堆积密度与颗粒配位数、粒径尺寸比和大颗粒体积分数的关系。国防科技大学的杨晋朝等[13]提出了一种粉末燃料高效装填方法, 可将粉末燃料的松装密度提高近10%, 然而其指出振实状态的粉末燃料不易于流化, 却未给出相关验证。
为了进一步提高粉末燃料的装填密度, 本文基于已有的颗粒堆积理论, 对不同粒径的铝粉进行级配振实装填, 研究了不同因素对装填率的影响规律, 同时对级配振实装填所得铝粉的均匀性和流化性能进行了检测分析和实验验证研究。实验所得结果可为粉末火箭发动机燃料储箱的粉体装填提供参考。
1 实验系统及原理
1.1 粉体样本
为了保证粉末火箭发动机的点火、燃烧性能, 实际中所使用的金属粉末燃料粒径一般为1~100 μm之间, 因而本文选取了该粒径范围内的5种不同粒径铝粉作为实验样本, 其实物图如图 1所示。
实验前对所用铝粉进行电镜扫描分析和激光粒度分析以获得实验样本球形度及粒径等参数的详细信息。各个型号样本的电镜扫描照片如图 2所示。总体说来, 1#~4#样本颗粒的形状较为规则, 球形度较好, 但仍然存在部分小颗粒附着于大颗粒表面的现象。5#样本颗粒的形状很不规则, 球形度较差, 颗粒之间相互干涉现象严重。
为了获得粉体样本的实际粒径分布参数, 使用Mastersizer-2000型激光粒度分析仪(英国Malvern公司产), 检测这5种粉末样本的粒度分布, 测试结果如图 3所示。
由图 3可以看出, 实际铝粉粒径并非单一值, 而是呈现正态分布。分析测试结果中D[4, 3],D[3,2]分别称为体积平均径和表面积平均径, 它们相差越大表示粒径分布越宽。d(0.1), d(0.5)和d(0.9)分别为粒度仪的10值、50值和90值(达到该百分比的粒度), 即粒径按从小到大排列, 10%, 50%和90%处颗粒的粒径大小, 因而d(0.5)值就代表中间粒径的大小。
根据分析测试结果, 1#~2#样本的粒径分布比较集中, 而3#~5#样本的粒径分布范围较宽。1#~4#样本的中间粒径与所期望直径非常接近, 而5#样本的中间粒径与期望值相差较大, 这可能与其形状不规则有关。
 |
图1 铝粉样本实物照片 |
 |
图2 铝粉样本电镜扫描照片 |
 |
图3 铝粉样本激光粒度分析测试结果 |
1.2 装填实验装置及装填率测量方法
图 4为粉体致密装填实验装置。实验系统主要由振动台、粉末储箱、活塞、搅拌棒、电子天平等组成。其中振动台购自浙江省上虞市智腾仪器设备厂, 型号为ZDT-800, 振动频率为2 860次/分, 振幅为0.3~0.6 mm。粉末储箱及活塞部分结构参数如表 1所示。
实验前首先用精密电子天平称量质量为mAl的铝粉, 并将其倒入粉末储箱中。使用搅拌棒搅拌一定时间使其掺混均匀, 之后用活塞压住, 以防止在振动过程中粉体弥散从而影响实际装填率测量计算精度。实验时接通振动台电源并使用秒表记录振动时间。实验结束后, 测量计算装填率。
装填率测量计算方法示意图如图 5所示。
测量露在储箱外的活塞杆长为X, 则储箱内铝粉高度为
从而振实后铝粉体积为
则其实际密装密度为
已知铝的密度为ρAl, 从而该铝粉样本实际密装装填率为
 |
图4 铝粉致密装填实验装置 |
粉末储箱及活塞部分结构参数
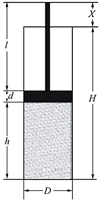 |
图5 装填率测量计算方法示意图 |
1.3 流化性能验证实验系统及原理
使用如图 6所示的粉末供给系统来验证振实装填后铝粉的流化性能。该系统由流化驱动气路、活塞驱动式储箱、气动球阀、位移传感器和背压模拟装置组成。活塞在驱动气的作用下向前推进, 同时流化腔内的粉末燃料与流化气形成气固两相流, 并经由气动球阀一起流出粉箱, 背压模拟装置用来建立一定的背压以模拟发动机工作时的燃烧室压强。活塞速度由进入驱动腔内的驱动气控制, 其相互关系如(5)式所示。
式中, 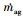 为驱动气质量流率, ρag为驱动腔内驱动气的密度, v为活塞速度, A为活塞的横截面积。
为驱动气质量流率, ρag为驱动腔内驱动气的密度, v为活塞速度, A为活塞的横截面积。
活塞位移测量采用德国FESTO公司生产的电位器式位移传感器, 该位移传感器输出信号大, 且能够实现在线采集, 其线性精度误差为0.05%。
在驱动气量保持不变的条件下, 若粉末燃料流化性能良好, 则由于活塞向前运动被挤到流化腔出口附近的粉末燃料会在流化气的作用下稳定的流出粉箱, 从而活塞会以设计的速度稳定前进。反之, 若粉末燃料流化性差, 则会导致到达流化腔出口处的粉末不能及时被带出粉箱, 从而堆积在粉箱出口, 导致粉末被压实, 并阻碍活塞的平稳推进, 具体表现为活塞位移的曲折振荡。因此, 本文将通过分析活塞位移曲线的走势来判定粉末流化性能的优劣。
 |
图6 粉末燃料供给系统构型 |
1.4 级配理论及实验工况
由颗粒堆积理论[14-16], 粉末颗粒级配装填时, 首先在容器中装填大颗粒(1级颗粒), 若已知大颗粒装填率为η1, 则在大颗粒间会形成1-η1的空隙率; 此时继续填入2级颗粒(装填率η2), 理想情况下, 2级颗粒刚好填充于1级颗粒形成的间隙, 则需填入2级颗粒的量为(1-η1)η2; 依此类推。因而可确定粉末级配装填时的理论最佳质量配比为
式中, md1, md2分别为1级颗粒和2级颗粒的装填质量; η1和η2分别为该2种粒径粉末的实际装填率。
计算表明[17], 单级球颗粒在六方最紧密排列情况下, 其间隙可容纳小颗粒的最大半径为0.224 7R。因而相邻粒级颗粒粒径比(小颗粒与大颗粒粒径之比)理论上至少应小于0.224 7。
由上述级配理论可知, 粉末颗粒装填率的大小与单一粒径粉体样本装填率和级配参数有关, 并且考虑到实际粉体振实装填过程中装填工艺和振动时间可能对粉体实际装填率产生一定的影响, 因而最终设置了如表 2所示的实验工况。首先对5种粒径铝粉分别进行振实装填, 获得其相应的致密装填率η, 从而由(6)式计算可得级配装填时的理论最佳质量配比。对于级配装填, 本文设置了3组对比实验工况来分别研究装填工艺、振动时间和级配参数对铝粉致密装填率的影响。其中工况1, 2和3探讨了不同装填工艺对装填率的影响; 工况3和4研究了振动时间对装填率的影响规律; 工况3,5,6,7和8验证了级配参数对装填率的影响; 工况9是在本文研究基础之上为获得更高的装填率而增加的一组实验工况, 并对该工况下所得铝粉进行了均匀性分析和流化性验证。
实验工况
2 实验结果与分析
2.1 单一粒径铝粉装填结果与分析
根据2.2节装填率测量计算方法对5种铝粉样本的致密装填率进行测量, 结果如图 7所示。
由图 7可以看出, 当颗粒粒径位于1~75 μm之间时, 随着粒径的不断增大, 其密装装填率随之上升, 其中15 μm的铝粉装填率比1 μm的铝粉装填率高了约25.4%;而15 μm, 40 μm和75 μm铝粉的装填率比较接近; 但所有粉体的实际装填率都小于等径颗粒粉体的理论装填率62%。理论上来说, 单一粒径球体的密装装填率(同一堆积方式下)应该相同。导致实验测得的不同粒径铝粉之间装填率差异的很重要的一个原因就是超细颗粒之间的干扰干涉作用。粒径越小, 这种颗粒间的作用力就越明显, 导致1 μm铝粉的装填率很低。然而从图 7中还发现100 μm铝粉的装填率低于15 μm, 40 μm和75 μm铝粉的装填率, 这是由于100 μm铝粉的颗粒形态很不规则, 球形度很差, 此时颗粒形态对装填率的影响占了主导地位, 导致其实际装填率的降低。
 |
图7 铝粉样本致密装填率 |
2.2 级配装填实验结果与分析
2.2.1 装填工艺对装填率的影响
表 3为不同装填工艺下的装填率。由工况1, 2对比可以看出, 分批填料方式所获得的装填率略高于整体填料方式, 但相差不大, 仅高了1.9%。究其原因, 整体填料方式与分批填料方式对粉体装填均匀性影响较小。而通过对比工况2, 3可以发现搅拌与否对装填率的影响较大, 分批填料加搅拌工艺下的装填率比分批填料无搅拌工艺下的装填率高了约9%。因而实际粉体装填时, 若要提高粉体装填率, 必须得将其先充分搅拌均匀后再振实。
不同装填工艺下的装填率
2.2.2 振动时间对装填率的影响
图 8为装填率随振动时间变化曲线。从图中可以看出, 在振动初期, 装填率随振动时间上升的幅度较大, 振动6分钟后, 装填率上升幅度较小, 8分钟后, 装填率达到最大值并保持不变。由于铝粉上面有活塞压着, 所以没有出现装填率下降的现象。
在振动初期, 由于颗粒间空隙较大, 颗粒间相接触的面积比较小, 从而相互之间的摩擦力、应力等都较小, 所以在外部振荡的激励下, 颗粒间的空隙迅速减小, 装填率显著提升。而随着空隙的逐渐减小, 颗粒间的斥力越来越大, 在相同的外部激励条件下, 颗粒越来越难靠近。直到最后, 粉体颗粒达到最大变形, 即使继续振动, 装填率也不会再上升。
因而在实际粉体装填时, 初期的振动对装填率的提升比较明显。随着振动时间的逐渐加长, 装填率的提升增益将很小。
 |
图8 致密装填率对振动时间变化曲线 |
2.2.3 级配参数对装填率的影响
不同级配参数下装填实验结果如表 4所示。其中工况3,5和6研究了质量配比对装填率的影响, 工况3,7和8研究了相邻粒级颗粒粒径比对装填率的影响。由于100 μm和15 μm铝粉的单一粒径装填率分别为57.26%和57.79%, 则根据公式(6), 100 μm/15 μm铝粉级配装填时的理论最佳质量配比为
同理可得100 μm/75 μm和100 μm/40 μm铝粉级配装填时的理论最佳质量配比分别为
由工况3, 5和6实验结果可以看出, 在实际质量配比偏离理论最佳质量配比过大(无论偏高还是偏低)的情况下, 粉体混合后的密装装填率都有所下降。质量配比偏高, 意味着大颗粒数量增多, 而小颗粒只能部分填充大颗粒的间隙, 多出来的大颗粒之间会留出许多空隙不被填充, 导致系统总的装填率下降。而质量配比变小, 意味着小颗粒数量增多, 在填满了大颗粒的间隙后还会剩出一部分的小颗粒, 这就相当于原本应该是大颗粒位置的地方替换为了一群小颗粒, 从而多出来很大一部分空隙, 从而局部装填率减小, 导致整体的装填率下降。
由工况3, 7和8可以看出, 相邻粒级颗粒粒径比对装填率的影响很大。对于工况7和工况8, 由于粒径比均大于0.224 7, 粉体系统处于挤塞状态, 即小颗粒尺寸过大, 不能刚好填充于大颗粒之间的空隙中, 粉体颗粒间的空隙仍然很大。而对于工况3, 颗粒尺寸比小于0.224 7, 小颗粒刚好填入大颗粒形成的间隙中, 导致系统整体的空隙率大大减小, 从而大幅提高了粉体装填率(约20%)。
所以, 应选取合适的级配参数, 尽量保证小颗粒刚好填满大颗粒间的空隙, 这样才能保证整体的装填率达到最大值。
不同级配参数下装填实验结果
2.3 致密装填铝粉均匀性分析及其流化性验证
在上述研究结果的基础之上, 考虑到100 μm, 15 μm和1 μm这3种粒径的铝粉相邻粒级颗粒粒径比(小颗粒与大颗粒粒径之比)分别为0.15和0.067, 均小于0.224 7, 因而使用100 μm, 15 μm和1 μm 3种粒径的铝粉进行3级粒径级配装填实验。结合公式(6), 求得理论最佳质量配比为
在该质量配比条件下进行致密装填实验, 最终获得了高达73.02%的致密装填率。
2.3.1 均匀性分析
对该工况所得铝粉进行取样分析。在其上层和下层各取一个样, 中层不同位置处取3个样, 共计5个样本, 对其进行激光粒度分析, 检测该装填工艺下所得铝粉在不同高度处及同一高度不同位置处的粒径分布均匀性。激光粒度分析测试结果如图 9所示, 分析激光粒度测试结果所得的各粒级铝粉体积含量分布见表 5。
从表 5可以看出, 对于不同高度处的铝粉样本, 上层各粒级颗粒含量与理想值较为接近, 而中、下层1 μm, 15 μm铝粉含量均高于理想值, 100 μm铝粉含量明显偏低。这说明在振动搅拌过程中, 细小颗粒很容易通过大颗粒间的空隙沉入到下层中, 而一旦小颗粒沉入下层之后, 便很难再进入上层, 同时也就意味着大颗粒很难进入下层, 从而导致中、下层细粉含量比较高, 而粗粉含量偏低。这也说明了本装填工艺搅拌均匀性并不是很好, 若采用更好的搅拌工艺, 进一步提高粉体级配装填的均匀性, 则将会获得更高的装填率。从图 9b)和表 5中均可发现对于同一高度不同位置处的铝粉样本, 各粒级颗粒质量含量基本相一致, 说明采用本装填工艺得到的铝粉在同一高度处的均匀性比较好。
 |
图9 致密装填铝粉均匀性分析测试结果 |
各粒级铝粉体积含量分布
2.3.2 流化性验证
使用图 6所示的粉末供给装置, 在0.5 MPa的背压下对工况9所得铝粉进行冷态供粉实验, 所得实验曲线如图 10所示。
从图中可以看出活塞位移一开始有所下降, 这有可能是由于球阀打开滞后导致流化腔内压强瞬间增大并超过驱动腔压强, 从而导致活塞后退。待球阀完全打开后, 流化腔压强迅速下降并恢复正常, 驱动腔与流化腔保持一定的压差并驱动活塞平稳前进, 整个工作过程持续8秒钟。在工作结束时, 活塞位移有明显的突跃, 这可能是由于球阀关闭滞后, 导致流化腔内残余气体继续排出粉箱, 导致活塞两侧压差迅速增大, 从而活塞向前突进。由图可以看出在工作过程中活塞位移曲线基本平稳, 未出现曲折振荡现象, 说明该铝粉流化性能较好, 能够在流化气的曳力作用下及时流出粉箱。活塞速度与设计值误差为3.6%, 由文献[18]可知, 若假设粉箱内粉体装填密度在工作过程中基本保持恒定, 则粉末质量流率与活塞移动速度呈正比关系, 从而粉末供给精度即为3.6%, 在误差允许范围之内, 能够满足粉末火箭发动机供粉要求。
 |
图10 流化性能验证实验曲线 |
3 结论
本文基于已有的颗粒堆积理论, 针对粒径范围在1~100 μm之间的5种铝粉样本进行致密装填实验研究, 探讨了不同因素对铝粉致密装填率的影响规律, 并分别对致密装填所得铝粉的均匀性及流化性进行了分析和验证, 得到的主要结论有:
1) 对粉体进行分批装填、搅拌和振动, 可以极大的提高粉体装填率; 初期的振动对装填率的提升比较明显, 随着振动时间的逐渐加长, 装填率的提升增益将逐渐减小;
2) 在进行颗粒级配装填时, 相邻粒级颗粒粒径比至少应小于0.224 7, 从而保证小颗粒能填充于大颗粒间形成的空隙。同时若其实际质量配比偏离理论最佳质量配比过大将会导致装填率降低。
3) 在m100 μm:m15 μm:m1 μm=6.89:2.97:1的级配参数下获得了73.02%的致密装填率。均匀性分析和流化性验证结果表明所得铝粉在同一高度处均匀性良好, 不同高度处均匀性还有待改善; 致密装填所得铝粉流化性能良好, 粉末供给精度达到了3.6%, 可满足粉末火箭发动机供粉要求。
References
- Zhang Shengmin, Yang Yuxin, Hu Chunbo. Experimental Investigation on Thrust Regulation of Powdered Rocket Motor[J]. Journal of Solid Rocket Technology, 2015, 38(3): 347-350 (in Chinese) [Article] [NASA ADS] [Google Scholar]
- Li Yue, Hu Chunbo, Sun Haijun, et al. Study on Flow and Combustion Characteristics in the Thrust Chamber of Powder Rocket[J]. Journal of Solid Rocket Technology, 2014, 37(6): 792-796 (in Chinese) [Article] [NASA ADS] [Google Scholar]
- Bernal J D, Mason J. Coordination of Randomly Packed Spheres[J]. Nature, 1960, 188: 910-911 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Scott G D. Packing of Equal Spheres[J]. Nature, 1960, 188: 908-909 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Scott G D, Kilgour D M. The Density of Random Close Packing of Spheres[J]. J Phys D Appl Phys, 1969, 2(6): 863-866 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Owe B T G, Mcdonald R L, Trainor R J. The Packing of Spheres[J]. Powder Technology, 1969, 3(1): 183-188 [Article] [CrossRef] [Google Scholar]
- Yerazunis S, Cornell S W, Wintner B. Dense Random Packing of Binary Mixtures of Spheres[J]. Nature, 1965, 207: 835-837 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Mcgeary R K. Mechanical Packing of Spherical Particles[J]. Am Ceram Soc, 1961, 44: 513-522 [Article] [CrossRef] [Google Scholar]
- Li L G, Kwan A K H. Packing Density of Concrete Mix under Dry and Wet Conditions[J]. Powder Technology, 2014, 253: 514-521 [Article] [CrossRef] [Google Scholar]
- Parteli J R, Schmidt J, Blumel C, et al. Attractive Particle Interaction Forces and Packing Density of Fine Glass Powders[J]. Scientific Reports, 2014, 4: 1-7 [Article] [Google Scholar]
- Wu Chengbao, Hu Xiaofang, Duan Baitao. Theoretical Calculation for Packing Density of Powder[J]. China Powder Science and Technology, 2009, 15(5): 76-81 (in Chinese) [Article] [Google Scholar]
- Ouyang Hongwu, Liu Yong, Wang Haibing, et al. Calculation Method for Random Packing of Sphere Particles[J]. Materials Science and Engineering of Powder Metallurgy, 2002, 7(2): 87-92 (in Chinese) [Article] [Google Scholar]
- Yang Jinzhao, Xia Zhixun, Hu Jianxin, et al. Study on High Efficiency Packing Technology of Powdered Fuel[J]. Journal of Solid Rocket Technology, 2013, 36(1): 37-44 (in Chinese) [Article] [Google Scholar]
- Stovall T, Delarrard F, Buil M. Linear Packing Density Model of Grain Mixtures[J]. Powder Technology, 1986, 48: 1-12 [Article] [CrossRef] [Google Scholar]
- Yu A B, Standish N. Porosity Calculations of Multi-Component Mixtures of Spherical Particles[J]. Powder Technology, 1987, 52: 233-241 [Article] [CrossRef] [Google Scholar]
- Westman A E R, Hugill H R. The Packing of Particles[J]. Am Ceram Sot, 1930, 13(10): 767-769 [Article] [CrossRef] [Google Scholar]
- Weymouth C A G. Effects of Particle Interference in Mortars and Concrete[J]. Rock Products, 1933, 25: 26 [Google Scholar]
- Sun H, Hu C, Zhang T, et al. Experimental Investigation on Mass Flow Rate Measurements and Feeding Characteristics of Powder at High Pressure[J]. Applied Thermal Engineering, 2016, 102: 30-37 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 铝粉样本实物照片 |
| In the text | |
 |
图2 铝粉样本电镜扫描照片 |
| In the text | |
 |
图3 铝粉样本激光粒度分析测试结果 |
| In the text | |
 |
图4 铝粉致密装填实验装置 |
| In the text | |
 |
图5 装填率测量计算方法示意图 |
| In the text | |
 |
图6 粉末燃料供给系统构型 |
| In the text | |
 |
图7 铝粉样本致密装填率 |
| In the text | |
 |
图8 致密装填率对振动时间变化曲线 |
| In the text | |
 |
图9 致密装填铝粉均匀性分析测试结果 |
| In the text | |
 |
图10 流化性能验证实验曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


