| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 21 - 27 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710021 | |
| Published online | 03 April 2019 | |
Lateral/Directional RCS Attitude Control for Lift Reentry Vehicle in Large Dynamic Pressure Regime
升力式再入飞行器大动压下横侧向RCS姿态控制方法研究
School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China
Received:
12
March
2018
For the existence of aerodynamic coupling and big turbulence of reentry vehicle in large aerodynamic flight status, Conventional method for RCS controller designing is difficult to track the bank angle command quickly and accurately. To solve the problem, according to the feature that the lateral/directional coupling is significant and the yaw channel is more effective and stronger to turbulence when tracking the bank angle, a strategy is proposed by using the roll and yaw channel simultaneously to control the bank angle dynamic. Double loop dynamic inversion controller is designed in which the bank angle loop conduct as outer loop and the roll and yaw angle rate loop as inner loop. The convergence of sideslip angle is guaranteed by improving the design of roll angle rate controller and the influence of the controller parameters to converge mode is analyzed. PWPF modulator is applied to convert command moment into pulse signals. Numerical simulation is carried out to verify the benefits of the proposed control method, the results shows that the present method solved the problem that RCS controller designed in conventional manner, and improve control ability of RCS in large aerodynamic condition.
摘要
针对升力式再入飞行器大动压下横侧向快速、高精度RCS姿态控制问题,利用再入飞行器在大攻角状态下横侧向耦合明显,偏航通道对倾侧角的控制更高效、抗干扰能力更强的特点,提出了同时控制滚转和偏航跟踪倾侧角指令的策略,设计了以倾侧角控制为外回路,以滚转和偏航角速率为内回路的双回路动态逆控制器。通过滚转角速率控制器的改进设计保证了侧滑角在不受控状态下的收敛性,并分析了控制参数选择对侧滑角收敛特性的影响。将该控制器与采用常规解耦方式设计的控制器进行了仿真对比,结果表明,该方法有效解决了采用常规RCS控制方法时倾侧角在大动压再入条件下响应慢、抗干扰能力差的问题,提高了RCS在大动压下的控制能力。
Key words: reentry vehicle / lateral flight control / reaction control system / dynamic inversion
关键字 : 再入飞行器 / 横侧向控制 / 反作用控制系统 / 动态逆
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
升力式再入飞行器具有高升阻比外形,能够从轨道空间进入稠密大气并借助空气动力减速滑翔和大范围机动实现特定任务,在航天领域具有重要的经济和军事价值。该类飞行器飞行空域和速域跨度极大,为满足控制需要,通常采用气动舵面加RCS(reaction control systems)的操控配置形式[1],在低动压时借助RCS控制稳定姿态,并随着动压的增大逐步过渡至气动舵面控制。在大动压段,由于飞行环境恶劣,飞行器面临严重的气动加热问题,舵面烧蚀和失效的风险显著增加,因此,研究大动压下再入飞行器RCS姿态控制的策略和方法,对于拓展RCS应用范围,提升再入飞行器控制系统的鲁棒性和容错能力,提高再入安全性具有积极意义。
对于再入飞行器的横侧向姿态控制而言,再入过程中飞行器的姿态需在正负间做大范围快速翻转。常规控制设计通过滚转通道控制倾侧角转动,通过偏航通道将侧滑角控制在零度附近以降低耦合影响。文献[2]研究了欠驱动构型再入飞行器横侧向耦合机理,利用飞行器上反效应设计了低动压下襟翼/RCS复合控制策略,取得了较好的跟踪效果;文献[3]将飞行器模型分为快慢回路分别进行设计并采用反演滑模控制方法设计了飞行器再入初期的RCS控制律;文献[4]采用一种带死区的乒乓控制方式设计了再入飞行器高空状态下的独立三通道RCS控制律;文献[5]采用模型跟踪神经网络自适应动态逆控制方法设计了可重复使用再入飞行器的气动/RCS复合姿态控制器。可以看出,但大多研究将RCS控制的使用范围局限于气动效应不明显的再入初期,控制设计上多采用常规策略,在大动压时由于RCS的滚转控制力矩有限,而通道间耦合和气动干扰严重,上述方法设计单纯RCS控制器难以满足横侧向对于快速性和精度的控制需求。
本文利用飞行器大攻角姿态动力学横侧向之间的耦合特性,提出同时控制飞行器滚转和偏航转动以提高倾侧角控制效率的控制策略,不同于常规的横侧向协调控制,本文中偏航方向的转动“超前”于滚转方向,使得飞行器倾侧角转动时诱导出有利的侧滑角,通过侧滑角在大攻角下对滚转力矩的强耦合效应加速飞行器滚动,形成偏航、滚转角速率和侧滑角协同实现倾侧角转动的控制结构。运用动态逆控制方法设计了以倾侧角控制为外回路,以滚转和偏航角速率为内回路的双回路控制器。为解决滚转、偏航角速率同时作为倾侧角控制量导致的侧滑角状态不受控问题,对滚转通道动态逆控制器进行了改进设计,采用部分反馈线性化方法保证了倾侧角趋于稳态时侧滑角的收敛,并分析了控制参数对侧滑角收敛特性的影响。最后,对所设计的控制律在SIMULINK仿真平台进行了数字仿真,仿真结果表明,所采用的控制策略和设计的控制器显著提高了再入飞行器对倾侧角指令的响应能力,增强了RCS控制的抗干扰性能,达到了对倾侧角跟踪精度的要求,具有良好的应用价值。
1 再入飞行器姿态控制建模
升力式再入飞行器的姿态动力学如(1)~(6)式所示,模型忽略了气动阻尼力矩对飞行器的影响,且由于不涉及气动舵面的控制问题,式中省略了舵面偏转所产生的力和力矩项。模型表达式中状态量α, β, μ, p, q分别表示攻角、侧滑角、倾侧角、滚转角速率、俯仰角速率和偏航角速率, 控制变量LR, MR, NR为RCS在滚转、俯仰、偏航方向产生的力矩。
上式的其他符号中, Δα=α-αT, αT为配平攻角。m表示飞行器质量, g0为重力加速度, Vf, γf分别为瞬时飞行速度和轨迹倾角, 在姿态控制系统的设计中, 由于速度和轨迹倾角相对姿态角和角速率为慢变量, 可认为是常值。L表示升力, Yβ, Lβ和Nβ分别表示侧向力、滚转和偏航力矩对侧滑角的偏导数。
再入飞行器三通道操纵力矩由8个喷管组合产生, 其配置方案如图 1所示。由3, 4号喷管产生正、负俯仰力矩, 由2、1号喷管产生正、负偏航力矩, 由6和8号、5和7号分别产生正负滚转力矩。俯仰、偏航和滚转控制力矩分别为150 Nm, 150 Nm和50 Nm, 最小开启时间10 ms, 开启延迟5 ms。
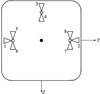 |
图1 飞行器RCS配置方案 |
2 双回路控制器设计
动态逆控制方法的主要原理是通过非线性反馈将非线性系统转化为线性形式, 然后在线性系统下设计输出变量的动态性能。本文基于时标分离原理, 将控制器分为慢回路和快回路分别进行设计。设计中通常要求快回路系统的带宽为慢回路的3~5倍, 这样快回路系统的响应时间相对慢回路可忽略不计, 整个系统实现近似非线性对消。
横侧向双回路动态逆控制器结构如图 2所示, 外回路(快)为倾侧角控制回路, 该回路输出经指令分配后, 产生期望的偏航和滚转角速率rc, pc。内回路(慢)分别为偏航角速率动态逆控制器和改进的滚转角速率控制器, 对应产生偏航和滚转通道指令力矩, 经脉宽脉频(pulse width pulse frequency, PWPF)调制器[6, 11]进行脉冲调制并结合喷管选择逻辑生成对应RCS喷管的开关指令。由结构图知, 该方法不包含侧滑角控制回路, 关于侧滑角的收敛问题由改进滚转角速率控制器解决。下面针对每个回路开展详细设计。
 |
图2 再入飞行器横侧向RCS姿态控制框图 |
2.1 外回路控制器设计
由文章第二部分再入飞行器建模的内容可知, 由于RCS配置的因素, 滚转通道RCS的控制力矩远不及偏航通道控制力矩大, 但机体纵轴惯量较小, 滚转RCS的控制更加灵敏。同时在大动压下, 侧滑角对滚转力矩的耦合项Lβ的大小远超过滚转RCS的操纵效率。因此, 本文控制设计将偏航角速率r和滚转角速率p一同作为控制变量, 目的在于结合2个通道优势提高倾侧角控制的效率和抗干扰性能。倾侧角动力学方程如(3)式所示, 将其写为如下形式
式中
定义倾侧角误差为:
对其求导, 并令误差动态满足如下关系式:
结合(7)式可得:
由于存在2个控制变量, g3(x1)不可直接求逆, 考虑到应让飞行器在转动中产生“有益”的侧滑角, 使得侧滑角耦合产生的滚转力矩方向与指令滚转角速率pc相一致, 根据该原则对控制指令进行分配。忽略(2)式中慢变量的作用, 得到侧滑角动态近似满足如下关系式:
根据上述原则, 需使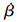 与r异号, 即
与r异号, 即
记(10)式右边为Δμ, 则控制指令pc, rc分配如下:
式中, 0 < λμ < 1, 根据关系式(11)可知, 应选择λμ > sin2α。
2.2 内回路控制器设计
完成倾侧角回路的设计后, 根据得到的控制指令pc, rc分别设计对应的内回路动态逆控制器, 用以产生滚转和偏航通道的RCS控制指令。首先设计偏航角速率控制律。偏航角速率动态方程如(6)式, 将其写为如下形式:
式中, , 定义偏航角速率误差:
, 定义偏航角速率误差:
令偏航角速率的误差动态满足关系式
结合(14)式可得偏航力矩指令NRc的表达式:
对于滚转角速率控制, 若采用同样设计进行非线性对消, 则会造成侧滑角β不受控, 其收敛性不能保证。这里采用部分非线性对消的方法, 保留滚转动态方程中的侧滑角耦合项。
记 , 重新将(4)式中的滚转角速率方程写出如下
, 重新将(4)式中的滚转角速率方程写出如下
假设期望的滚转角速率误差动态
结合(18)式可得LRc的表达式为
由于不包含侧滑角的耦合项, 实际滚转角速率动态
从该式可以看出, 侧滑角耦合产生的附加滚转角速率总是朝着消除侧滑角的方向转动。为分析侧滑角的收敛特性, 假设:①在倾侧角接近稳态时, pc,  都较小, 可忽略; ②偏航角速率r只与倾侧角跟踪有关, 与侧滑角β的状态无关, 可视作干扰量。此时滚转角速率对侧滑角的影响占主导地位, 忽略(2)式中与侧滑无关的慢变量部分, 侧滑角动态方程可简化为
都较小, 可忽略; ②偏航角速率r只与倾侧角跟踪有关, 与侧滑角β的状态无关, 可视作干扰量。此时滚转角速率对侧滑角的影响占主导地位, 忽略(2)式中与侧滑无关的慢变量部分, 侧滑角动态方程可简化为
滚转角速率动态方程可进一步简化为
联立得到以β和p为状态量的线性微分方程组
式中,b4=-Yβ/(mVf), 可求得系统(24)的特征方程为
显然, 由于kPp > 0, Lβ′ < 0且b4 > 0, 系统的特征根实部小于零, 在偏航角速率r趋于零后, 能够自然收敛到零状态。分析可知, 当kPp < Lβ′sinα/b4+b4时, 增大kPp的值可以同时增加特征模态的阻尼与频率。为实现对侧滑角收敛特性的完全配置, 可在滚转控制律酌情(Lβ′幅值过小)引入辅助项-kPββ, 起到增大Lβ′的效果, 通过kPp与kPβ参数的协调选取可令侧滑角动态具有满意的特征模态。
3 仿真验证
为验证本文中控制方法的有效性, 基于前述模型进行了数字仿真验证。取飞行器再入过程中状态点H=50 km, Vf=3 300 m/s, 配平攻角αT=38.72°, 此时飞行动压q=5 323 Pa, Lβ′=-24.1, b4=0.005。控制参数kPμ=1, λμ=0.5, kPr=8, kPp=10, kPβ=0。倾侧角指令为幅值40°,占空比50%,周期20 s的方波经由时间常数为0.4 s的一阶滤波环节形成的信号。为了对比本文控制方法相对采用常规控制思路设计的控制器在大动压下的优越性, 设计了基于μ→p,β→r常规控制模式的动态逆控制器。将仿真分为无扰和扰动情况分别对2种方法所得结果进行比较。
无扰动情况下2种控制器性能对比如图 3~8所示。图中下标“norm”表示常规动态逆方法,无下标曲线为文中所用方法。由图 3可以看出,在控制器设计指标相同的情况下,2种方法设计的控制器对倾侧角指令的动态响应都表现良好,其中常规设计方法的倾侧角控制误差为±0.5°,略小于本文方法的±1°。这是由于常规方法对系统非线性的抵消更彻底,且滚转RCS控制更加灵敏的缘故。由图 4侧滑角曲线的对比可以看出2种方法的差异,常规方法在倾侧角滚动过程中首先产生了阻碍机体滚动的正侧滑角,后在侧滑角控制器的作用下经一次振荡收敛至零,而本文方法由于偏航运动在倾侧角滚动过程中起主导作用,期间产生的侧滑角为利于机体滚动的负侧滑角,且在侧滑角收敛过程中不存在振荡现象。
图 5和图 6分别为滚转和偏航角速率曲线,可以看出,本文方法的滚转速率滞后于常规方法,体现了偏航超前的原则。图 7和图 8为2种控制器产生滚转和偏航力矩指令的对比图,从图中可以看出常规方法产生的最大滚转力矩指令为48 N·m,最大偏航力矩指令为130 N·m,接近饱和,而本文方法的最大滚转力矩指令33 N·m,最大偏航力矩指令94 N·m,说明在系统动态响应性能相同的情况下,本文方法优化了RCS控制指令,效率更高。
实际情况中,由于气动外形和质心不对称以及外界干扰的作用,飞行器会受到建模以外的力矩影响,为验证2种控制方法对于干扰力矩的抵抗能力,对滚转通道施加-40 N·m、偏航通道-20 N·m的常值干扰力矩,其他条件不变。
由图 9倾侧角曲线的对比可以看出,常规控制下无法产生足够的控制量抵消干扰的影响,指令跟踪呈现出发散状态,而本文方法在干扰的影响下仍然保持了良好的动态品质,仅造成倾侧角跟踪误差增大至±2.5°,此误差不致影响制导系统的稳定性,处于可接受范围。由图 10可以看出,本方法之所以克服了干扰力矩的影响,是由于偏航主导倾侧角跟踪时产生了额外的侧滑角,起到了抑制干扰力矩的作用。
 |
图3 无干扰情况倾侧角跟踪对比曲线 |
 |
图4 无干扰情况侧滑角对比曲线 |
 |
图5 无干扰情况滚转角速率对比曲线 |
 |
图6 无干扰情况偏航角速率对比曲线 |
 |
图7 无干扰情况滚转力 |
 |
图8 无干扰情况偏航力矩指令对比曲线矩指令对比曲线 |
 |
图9 有干扰情况倾侧角跟踪对比曲线 |
 |
图10 有干扰情况侧滑角对比曲线 |
4 结论
本文研究了升力式再入飞行器大动压状态下横侧向RCS姿态控制问题。针对常规构型的横侧向RCS控制在大动压情况时效率低下抑制干扰能力差的弱点,提出了用滚转和偏航通道联合进行倾侧角控制,利用偏航控制的力矩优势和侧滑角对滚转力矩的强耦合效应,达到高效控制倾侧角和增强飞行器抗干扰能力的目的。运用动态逆控制设计方法,首先设计了外回路倾侧角控制器,将得出的控制量根据偏航超前的原则进行了指令分配,产生偏航和滚转角速率指令;然后以偏航和滚转角速率作为内回路分别设计了控制器,为保证侧滑角的收敛,对滚转角速率回路的控制律进行了改进,并分析了改进后的侧滑角收敛特性,给出了相关参数的设计依据。对所设计控制律进行了无扰和干扰条件下的数字仿真,并与常规构型的控制器进行了对比。仿真结果说明,在相同的系统响应速率相当的情况下,本文提出的控制结构相对常规构型产生的指令力矩更小,起到提高RCS使用效率,缓解喷流饱和的作用;在受到较大干扰力矩影响使得常规构型控制发散的情况下,本方法能够有效抑制干扰,保持良好的动态跟踪品质并将跟踪误差限制在较小范围内。
References
- Fang Yuanpeng. Reaction Control System Control Method for Reusable Launch Vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(suppl 1): 97-101 (in Chinese) [Article] [Google Scholar]
- Shi Linan, Li Huifeng, Zhang Ran. Gliding Reentry Vehicle Lateral/Directional Coupling Attitude Control Strategy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 120-129 (in Chinese) [Article] [Google Scholar]
- Guo Jianguo, Zhang Tianbao, Zhou Jun, et al. Reaction Control System Design for Reentry Vehicle[J]. Journal of Solid Rocket Technology, 2017, 40(4): 511-516 (in Chinese) [Article] [Google Scholar]
- He Chenglong, Chen Xin, Wu Liaoni. Research on Attitude Control of Reaction Control System for Reusable Launch Vehicle[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(1): 51-54 (in Chinese) [Article] [Google Scholar]
- Mathavaraj S, Omkar Halbe, Radhakant Padhi. Robust Control of a Reusable Launch Vehicle in Reentry Phase Using Model Following Neuro-Adaptive Design[R]. AIAA-2010-8312 [Article] [Google Scholar]
- Chen Haibing, Zhang Shuguang, Fang Zhenping. Implicit NDI Robust Nonlinear Control Design with Acceleration Feedback[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 597-603 (in Chinese) [Article] [CrossRef] [Google Scholar]
- Wang Xiaoting, Zhou Jun, Lin Peng. Proposing Moving Centroid/RCS Control Strategy for Reentry Flight Vehicle[J]. Journal of Northwestern Polytechnical University, 2011, 29(2): 212-216 (in Chinese) [Article][Article] [Google Scholar]
- Ning Guodong, Zhang Shuguang, Fang Zhenping. Research on the Reaction Control System for Spacecraft Re-Entry Flight[J]. Flight Dynamics, 2005, 23(3): 16-20 (in Chinese) [Article] [Google Scholar]
- Lu Yanhui, Zhang Shuguang. An Improvement on PWPF Modulation of Discrete RCS and Design of the Blended Control Logic[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1561-1570 (in Chinese) [Article] [Google Scholar]
- Wu Hongxin, Meng Bin. Review on The Control of Hypersonic Flight Vehicles[J]. Advances in Mechanics, 2009, 39(5): 756-765 (in Chinese) [Article] [Google Scholar]
- Liu Jun, Hiang Yimin, Sun Chunzhen, et al. Research on Attitude Control of Reaction Control System for Hypersonic Vehicle[J]. Oranance Industry Automation, 2014, 33(3): 47-50 (in Chinese) [Article] [Google Scholar]
- Krovel T D. Optimal Tuning of PWPF Modulator for Attitude Control[D]. Trondheim, Norway, Norway University of Science and Technology, 2005 [Google Scholar]
- He Jingjing, Qi Ruiyun, Jiang Bin, et al. Fault-Tolerant Control with Mixed Aerodynamic Surfaces and RCS Jets for Hypersonic Reentry Vehicles[J]. Chinese Journal of Aeronautics, 2017, 30(2): 780-795 [Article] [CrossRef] [Google Scholar]
- Elmar M W, Klaus H W. Attitude Control of a Reentry Vehicle with Internal Dynamics[R]. AIAA-2002-4647 [Article] [Google Scholar]
- Dacosta R R, Chu Q P, Mulder J A. Reentry Flight Controller Design Using Nonlinear Dynamic Inversion[J]. Journal of Spacecraft and Rockets, 2003, 40(1): 64-71 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Mooij E. Adaptive Lateral Flight Control for a Wings Re-Entry Vehicle[R]. AIAA-2003-5322 [Article] [Google Scholar]
- Ramses M A. Robust Failure Detection for Reentry Vehicle Attitude Control Systems[J]. Journal of Guidance Control and Dynamic, 1999, 22(6): 839-845 [Article] [CrossRef] [Google Scholar]
All Figures
 |
图1 飞行器RCS配置方案 |
| In the text | |
 |
图2 再入飞行器横侧向RCS姿态控制框图 |
| In the text | |
 |
图3 无干扰情况倾侧角跟踪对比曲线 |
| In the text | |
 |
图4 无干扰情况侧滑角对比曲线 |
| In the text | |
 |
图5 无干扰情况滚转角速率对比曲线 |
| In the text | |
 |
图6 无干扰情况偏航角速率对比曲线 |
| In the text | |
 |
图7 无干扰情况滚转力 |
| In the text | |
 |
图8 无干扰情况偏航力矩指令对比曲线矩指令对比曲线 |
| In the text | |
 |
图9 有干扰情况倾侧角跟踪对比曲线 |
| In the text | |
 |
图10 有干扰情况侧滑角对比曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


