| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 28 - 34 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710028 | |
| Published online | 03 April 2019 | |
A Numerical Method for Estimating the Nonlinear Eigenvalue Numbers of Boundary Element
一种估计边界元非线性特征值数目的数值方法
School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China
Received:
2
March
2018
Recently, some new proposed methods for solving nonlinear eigenvalue problems (NEPs) have promoted the development of large-scale modal analysis using BEM. However, the efficiency and robustness of such methods are generally still dependent on input parameters, especially on the parameters related to the number of eigenvalues to be solved. This limitation obviously restricts the popularization of the practical engineering application of modal analysis using BEM. Therefore, this paper develops a numerical method for estimating the number of nonlinear eigenvalues of the boundary element method. Firstly, the interpolation method based on the discretized Cauchy integral formula of analytic function is used for obtaining the BEM matrix's derivative with regard to frequency, and this method is easily combined with the mainstream fast algorithm libraries of BEM. Secondly, the method for evaluating the eigenvalue number of BEM under various boundary conditions is obtained by combining the interpolation method with the analytic formula to obtain the eigenvalue number, while the unbiased estimation is used to determine the trace of matrix. Finally, a series of typical examples are used to explore the principle for selecting optimal input parameters in this method, and then a set of optimal input parameters are determined. The overall excellent performance of this method is verified by a complex large-scale example.
摘要
近年来,一些新提出的非线性特征值解法很好地推动了大规模边界元模态分析问题的发展,但这类方法的效率和鲁棒性还普遍依赖于输入参数的选取,特别是与待求解特征值数目相关的参数,这一局限性也明显制约了边界元模态分析方法向实际工程应用的推广。围绕这一问题,发展了一种通用的边界元非线性特征值数目估计方法。首先,针对特征值数目解析计算公式中边界元矩阵关于频率求导困难的问题,采用解析函数的Cauchy积分公式,发展了一种非常易于同主流边界元快速算法库结合的边界元矩阵关于频率导数的插值计算格式;其次,将该插值计算格式与特征值数目解析计算公式结合,并通过无偏估计确定矩阵的迹,获得了适用于各类边界条件的边界元非线性特征值数目估计方法;最后,采用典型算例探索新方法最优输入参数的选取原则,并确定出了一组最优输入参数,而且通过大规模复杂算例对该方法具有的整体优异性能进行了验证。
Key words: boundary element method / modal analysis / nonlinear eigenvalue number / Cauchy integral formula / unbiased estimation
关键字 : 边界元 / 模态分析 / 非线性特征值数目 / Cauchy积分公式 / 无偏估计
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
边界元法[1](boundary element method, BEM)是一种重要的工程数值方法,特别适合处理以声学问题为代表的各类无限域、半无限域问题。然而,传统的BEM系统矩阵为满阵,计算量和存储量都很大,难以处理大规模问题。但近年来随着各类BEM快速算法的发展日趋成熟,应用BEM对大规模复杂工程结构进行分析的效率已大为提高[2]。目前,BEM已被广泛应用于声学、电磁学、传热学以及弹性动力学等领域,且在各类无限域、半无限域问题的仿真分析中表现出了一定的优势,如减振降噪设计中对声场的计算[3]。在减振降噪分析中,通常需要对声场进行模态分析以获得其固有频率和振型。对采用BEM离散的声场进行模态分析相当于求解如下形式的非线性特征值问题[4], 这也是制约这些方法集成到成熟商用分析软件而被广泛使用的原因之一。
目前, 已有学者针对如何高效获得给定频率区域内非线性特征值系统的特征值数目这一课题展开研究, 并已取得了初步成果, 文献[8]就提出了一种基于解析矩阵值函数的史密斯格式的特征值数目估计方法, 由于采用了无偏估计来获得矩阵的迹, 该方法的效率很可观, 非常适合处理大规模非线性特征值问题。但是, 由于该方法的实现过程需要执行T′(z)·v操作, 其中T′(z)为T(z)关于z的导数, v∈Cn×1为向量, 因此其并不能直接处理BEM非线性特征值问题。这是因为:边界元系数矩阵T(z)为非对称满阵, 当问题规模较大时, 必须采用快速算法进行加速, 而各类快速算法的基础就是T(z)远场子矩阵的可低秩近似特性, 如果直接计算T′(z), 这一特性将会消失, 从而导致快速算法失效, 也就无法应用于大规模边界元分析。
为解决上述问题, 本文提出一种基于解析函数Cauchy积分公式的BEM矩阵插值方法, 可以在复平面内任意单连通闭合区域内对T(z)进行高精度插值近似。在此基础上, 发展出了一种针对T′(z)·v的高精度插值方法, 该方法可以与文献[8]提出的估计非线性特征值数目的方法结合, 实现大规模BEM非线性特征值数目的估计。本文提出的这种方法无需显式计算T′(z), 也无需推导不同物理问题以及不同边界条件下T(z)各元素的表达式关于z的导数, 可以与现有的各类快速BEM程序包结合, 具有很强的通用性。而且, 由于插值点预先给定, 计算插值系数的过程也非常适合并行, 该方法也具有较高的计算效率。
1 确定BEM非线性特征值数目
本文以声学BEM为例[9], 考虑其非线性特征值问题, 但所提之方法具有通用性, 也适用于弹性动力学BEM、电磁学BEM等。
声学问题的边界积分方程为
式中, D为声场区域, ∂D为D的边界, p为声压, 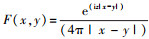 是三维Helmholtz方程的基本解,
是三维Helmholtz方程的基本解,  c(x)为自由项, 当∂D在x附近光滑时, c(x)=1/2, ny表示y点处的外法向。
c(x)为自由项, 当∂D在x附近光滑时, c(x)=1/2, ny表示y点处的外法向。
采用文献[10]的Nyström边界元法离散方程式, 最终可得如下标准形式的边界元离散方程
式中, H和G是边界元离散矩阵, p和q分别是包含节点声压及其法向导数的列向量。矩阵H和G中的近场修正部分仍需要进行常规边界元法中的奇异和近奇异积分计算。本文奇异积分采用文献[11]中的数值计算方法, 而近奇异积分采用逐步细分的方法来计算。
考虑Robin边界条件
当α≠0, β=0时, (3)式退化成Dirichlet边界条件, 当α=0, β≠0时, (3)式退化成Neumann边界条件。
下面考虑吸声结构分析中常见的一类Robin边界条件, 即阻抗边界条件
式中, Z为边界声阻抗, 与节点位置x和频率z有关; ρ0为声场介质密度。(4)式在每个边界元节点xj上都成立, 将这些式子统一写成矩阵形式即为
式中, B(z)是维度为n×n的对角矩阵, 其对角线元素表示为-iρ0ω/Z(xj, z)。将(5)式代入(2)式, 可得
(6) 式即为吸声结构模态分析中所要求解的特征方程, 系统矩阵T(z)=H(z)-G(z)B(z)。Dirichlet和Neumann边界条件所对应的特征方程可类似得到。
BEM中, 矩阵T(z)的元素是由基本解或其法向导数经单元积分后得到的。由于基本解是频率z的复杂函数, 再考虑到吸声结构中各类复杂阻抗边界条件的引入, 从而导致BEM特征值问题成为一种典型的非线性特征值问题。
文献[8]指出, 矩阵T(z)在复平面上给定的单连通闭合区域Ω内的特征值数目m可以通过下式表示
式中, tr(T(z))表示矩阵T(z)的迹, T′(z)表示关于z的导数, Γ表示Ω的边界。可以看出, 直接运用上式估计特征值密度需要进行矩阵求逆以及大量矩阵乘法运算, 计算效率十分低下, 无法应用于大规模非线性特征值问题。
为了避免这一情形, 文献[8, 13-14]提出通过无偏估计来获得矩阵迹的方法
式中, vl为采样向量, 其元素均由1和-1组成, 且等概率分布, L为采样向量数目, 各采样向量线性无关。将(8)式带入(7)式可得
通过数值积分公式离散上式
式中, 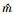 为估计出的特征值数目, N为积分点数目, zj为第j个积分点, wj为相应权重, 本文采用Gauss积分公式离散(9)式。
为估计出的特征值数目, N为积分点数目, zj为第j个积分点, wj为相应权重, 本文采用Gauss积分公式离散(9)式。
2 Cauchy插值
前文提到, 对T(z)关于z进行求导会导致边界元快速算法失效, 无法应用于大规模边界元非线性特征值问题。为解决这一问题, 本节基于解析函数的Cauchy积分公式构造了边界元矩阵T(z)的高精度插值近似格式, 在此基础之上构造了T′(z)的插值近似格式。
由于T(z)为全纯函数, 因此可以由Cauchy积分公式表示为
式中, Γ为复平面内任意积分路径, 此处将其与(8)式的积分路径取为一致, 采用Gauss数值积分离散上式
称(12)式为矩阵值函数T(z)的第一类Cauchy插值公式[15]。式中, 插值项数d决定插值精度, 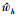 为积分点对应的权重, 它们由所采用的数值积分公式确定。
为积分点对应的权重, 它们由所采用的数值积分公式确定。
通过(12)式可以在复平面内对T(z)进行插值近似, 但是, 当z逼近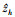 时,
时, 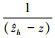 趋于无穷大, 式的精度会迅速下降, 导致插值失败。针对这一现象, 用
趋于无穷大, 式的精度会迅速下降, 导致插值失败。针对这一现象, 用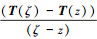 代替(11)式中的
代替(11)式中的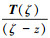 , 前者在z逼近ζ时分子分母同时趋于0, 不存在奇异性, 且其Cauchy积分值为0, 即
, 前者在z逼近ζ时分子分母同时趋于0, 不存在奇异性, 且其Cauchy积分值为0, 即
通过Gauss积分离散上式可得
整理上式可得T(z)的表达式如下
称(15)式为第二类Cauchy插值公式, 式中
对(15)式左右两端同时关于z求导可得
式中
将(17)式代入(10)式可得
根据(19)式可以看出, (10)式中的T′(z)vl可以通过一系列边界元矩阵向量乘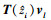 与插值系数φi′(z)线性组合而成。如此, 不仅避免了对T(z)直接求导, 使得(9)式可以应用于大规模边界元非线性特征值问题, 而且还极大增强了程序的通用性, (19)式与T(z)各元素的具体表达式无关, 只与其数值有关, 因此其既适用于各类边界条件的声学边界元, 也适用于其他诸如弹性动力学边界元、电磁学边界元等。
与插值系数φi′(z)线性组合而成。如此, 不仅避免了对T(z)直接求导, 使得(9)式可以应用于大规模边界元非线性特征值问题, 而且还极大增强了程序的通用性, (19)式与T(z)各元素的具体表达式无关, 只与其数值有关, 因此其既适用于各类边界条件的声学边界元, 也适用于其他诸如弹性动力学边界元、电磁学边界元等。
实际应用中, 插值项数d的取值对计算精度和效率的影响非常显著, 在保证插值精度的前提下, 选择尽可能小的d可以显著提高算法的效率。
文献[6]提出了一种通过基本解的插值误差来衡量T(z)插值精度的方法, 其核心思想是当边界元网格上场点x和源点y的距离|x-y|最大时, T(z)中对应位置处的元素t(z)在频域内振荡最为剧烈, 即只要此处的插值精度满足要求, 那么整个边界元矩阵T(z)的插值精度也将满足要求。|x-y|最大值不会超过几何模型的特征尺寸R, T(z)各元素的具体表达式视边界条件而定, 但均由基本解及其关于z的导数组合而成, 很容易获得。
如果给定频率区域上的最大允许插值误差为ζ, 插值项数初值为d0, 那么用上述方法确定最优插值项数的过程可以通过(20)式描述, 给定插值精度要求ζ, 从d0开始, 依次增大dh, h=0, 1, 2, …的取值直到(20)式成立, 此时的dh即为d的最优取值, 为了增大d的可靠性, 也可以对其进行适当放大。
式中, 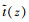 和t(z)分别表示Cauchy插值得到的矩阵元素值和直接计算得到的矩阵元素值。
和t(z)分别表示Cauchy插值得到的矩阵元素值和直接计算得到的矩阵元素值。
虽然本文需要确定的是对T′(z)进行插值的最优插值项数, 但考虑到导函数的阶数不会超过原函数, (20)式的结果同样可以指导对T′(z)进行插值时最优插值项数的选取, 而且还可以避免当核函数或边界条件表达式过于复杂时对T(z)元素求导困难这一问题, 如弹性动力学BEM的核函数[16]和声学BEM中的Delany-Bazley阻抗边界条件[17], 更有利于增强算法的通用性。
3 算例
本文的所有BEM模型都采用六节点二次曲面三角形单元离散, 快速算法选择核无关快速定向压缩算法, 精度设定为1.0×10-6, 线性方程组的求解采用GMRES算法, 收敛残差为1.0×10-6, 选择对角块预处理技术, 统一起见本文的积分路径均取为矩形, 矩阵Cauchy插值的截断误差也均为1.0×10-6。
3.1 验证矩阵插值精度
该算例目的在于验证本文构造的Cauchy插值公式的正确性以及插值项数d的估计策略的有效性。选择一单位立方体内声腔, 将其离散为300个边界单元, 共计1 800自由度, 关注波数范围为(2-2i, 10+2i)m-1, 积分路径选为矩形。首先, 分别对Dirichlet边界T(z)=G和Neumann边界T(z)=H中振荡最为激烈的矩阵元素的函数项tG=eizR/R和tH=keizR/R以及它们的导数tGD=ieizR和tHD=(1+ikR)eizR/R进行Cauchy插值, 根据(21)式绘制插值误差随插值项数的变化曲线, 见图 1。
根据图 1可知, 无论是Dirichlet边界还是Neumann边界, tG和tH的插值误差随插值项数的变换规律分别也可以描述tGD和tHD的插值误差随插值项数的变换规律。
接下来, 为进一步考察对T′(z)的插值精度, 将该模型所有表面均设定为Dirichlet边界, 且根据图 1可知, 当d=30时, T′(z)中振荡最为激烈的元素的最大插值误差小于1.0×10-6, 即插值精度达到快速算法精度, 根据(18)式计算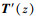 , 并通过(21)式计算复平面内的Cauchy插值误差, 绘制误差云图见图 2。通过图 2可以看出积分路径内T′(z)的插值误差稳定在1.0×10-6~1.0×10-5之间, 即第3节提出的对插值项数d的估计策略是有效的, 同时也证明通过Cauchy插值计算BEM系统矩阵导数这一方法可行。
, 并通过(21)式计算复平面内的Cauchy插值误差, 绘制误差云图见图 2。通过图 2可以看出积分路径内T′(z)的插值误差稳定在1.0×10-6~1.0×10-5之间, 即第3节提出的对插值项数d的估计策略是有效的, 同时也证明通过Cauchy插值计算BEM系统矩阵导数这一方法可行。
式中, 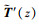 表示插值得到T(z)关于z的导数, T′(z)表示直接计算出的T(z)关于z的导数, y表示一随机向量。
表示插值得到T(z)关于z的导数, T′(z)表示直接计算出的T(z)关于z的导数, y表示一随机向量。
 |
图1 振荡最剧烈核函数及其导数的Cauchy插值误差随插值项数变化规律 |
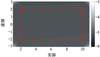 |
图2 复平面内T′(z)的Cauchy插值误差 |
3.2 验证估计结果的正确性
选择3个不同边界条件的基准模型验证本文提出的特征值数目估计方法的正确性和鲁棒性; 同时观察积分点数N和采样向量数L对计算结果的影响, 给出最优的N和L的取值方案。
第一个模型选择Dirichlet边界的单位球内声腔, 将其离散为622个边界单元, 共计3 732自由度, 关注波数范围为(3-1i, 9+1i)m-1; 第二个模型选择Robin边界的单位立方体内声腔, 将其离散为300个边界单元, 共计1 800自由度, 其中一对相互平行的表面为Dirichlet边界, 其余4个面为Neumann边界, 关注波数范围为(3-1i, 8+1i)m-1; 第3个模型选择一频变阻抗边界的长方体内声腔模型, 其长、宽、高分别为0.5 m, 0.4 m和0.3 m, 将其离散为332个边界单元, 共计1 992自由度, 在其中一个0.4 m×0.3 m的表面上敷设多孔吸声材料, 等效为Delany-Bazley阻抗边界条件[17], 其余表面为Neumann边界, 关注波数范围为(5+0i, 14+3i)m-1。前2个算例的实际特征值数目分别为29和12[18], 第3个算例的特征值数目为[17]。
首先, 根据第3节提出的方法绘制图 3, 通过图 3估计出这3个模型的最优插值项数d分别为26, 22和20。接下来通过改变参数观察积分点数N和采样向量数L对特征值估计结果的影响, 见表 1、表 2。
前文已经提到, 本文对特征值数目的估计结果主要用于为后期模态分析时输入参数的选择提供参考, 对估计结果不要求很准确, 所以N和L的取法也不要求精度很高, 观察表 1和表 2可以发现, 取N=10即可满足结果的可靠性要求, 至于L, 其最优取值应该在5~10之间。而对于特征值数目要求很准确的情况, 由于(11)式中的Gauss积分是指数收敛的, 只需要适当增加N, 特征值数目的估计精度就可以显著提高。
N的取值决定了(10)式中积分的精度, L的取值则是决定了(8)式中通过无偏估计获得的矩阵迹的准确程度。实质上, N和L的取值是依赖于矩阵元素关于频率振荡的激烈程度的。当关注频段范围过大, 或是频率非常高, 即矩阵元素关于频率振荡过于激烈时, 适当增加N和L的取值可以确保结果更为可靠。
 |
图3 3个基准模型最大Cauchy插值误差 |
采样向量数目L对估计结果的影响(N=30)
积分点数N对估计结果的影响(L=15)
3.3 实际工程算例
为了考察本文方法对于大规模复杂实际工程算例的适应性, 选择文献[5]提供的汽车驾驶室内声腔BEM模型对其分析, 见图 4, 该模型共计59 100自由度, 全部边界均为Neumann边界。文献[5]给定采样点数为200, 右端项数为2, 运用RSRR非线性特征值解法计算出该模型在40~500 Hz范围内共计有64个特征值。将本文的非线性特征值数目估计方法同上述算例中的RSRR方法结合, 在保持计算结果可靠的前提下, 可以显著提高其分析效率和鲁棒性。
运用本文的非线性特征值数目估计方法对该模型进行估计。首先, 根据(20)式绘制插值误差随插值项数的变化曲线, 见图 5, 并确定d=36, 根据算例4.2中描述的特征值数目估计结果同N和L的关系, 分别给定N=10以及L=5, 频率范围为(40-50i, 500+50i)Hz, 估计出该范围内的特征值数目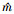 =67.671 9, 可以发现其与真实特征值数目非常接近。
=67.671 9, 可以发现其与真实特征值数目非常接近。
 |
图4 汽车驾驶室内声腔BEM模型 |
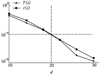 |
图5 汽车驾驶室内声腔模型最大Cauchy插值误差 |
4 结论
本文以声学边界元为例,发展了一种通用的估计大规模边界元非线性特征值数目的数值方法。而且,由于本文给出了系统矩阵求导的统一表达式,因此该方法也并不局限于边界元问题,对于一些系统矩阵难以获得或是矩阵元素关于频率求导困难的问题仍然适用。
1) 基于解析函数的Cauchy积分公式,建立了BEM矩阵关于频率导数的高精度插值格式,且该格式非常易于同主流的BEM快速算法库结合;
2) 将本文构造的插值格式与现有的特征值数目估计方法结合,实现了各类边界条件下BEM特征值数目的准确估计;
3) 通过典型算例探索,分别提出了本文方法最优输入参数的选取原则,并且根据该原则,结合快速算法,准确估计出了大规模复杂BEM模型的特征值数目。
References
- Yao Zhenhan, Wang Haitao. Boundary Element Method[M]. Beijing, Higher Education Press, 2010 [Google Scholar]
- Liu Y J, Mukherjee S, Nishimura N, et al. Recent Advances and Emerging Applications of the Boundary Element Method[J]. Applied Mechanics Reviews, 2011, 64(3): 1001 [Article] [Google Scholar]
- Dominik B, Michael J, Lothar G. A Comparison of FE-BE Coupling Schemes for Large-Scale Problems with Fluid-Structure Interaction[J]. International Journal for Numerical Methods in Engineering, 2010, 77(5): 664-688 [Article] [Google Scholar]
- Mehrmann V, SchrÖder C. Nonlinear Eigenvalue and Frequency Response Problems in Industrial Practice[J]. Journal of Mathematics in Industry, 2011, 1(1): 1-18 [Article] [CrossRef] [Google Scholar]
- Xiao J, Meng S, Zhang C, et al. Resolvent Sampling Based Rayleigh-Ritz Method for Large-Scale Nonlinear Eigenvalue Problems[J]. Computer Methods in Applied Mechanics & Engineering, 2016, 310: 33-57 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Wang Junpeng, Xiao Jinyou, Wen Lihua. An Efficient Numerical Method for Large-Scale Modal Analysis Using Boundary Element Method[J]. Chinese Journal of Theoretical & Applied Mechanics, 2017, 49(5): 1070-1080 (in Chinese) [Article] [Google Scholar]
- Zheng C, Zhang C, Bi C, et al. Coupled FE-BE Method for Eigenvalue Analysis of Elastic Structures Submerged in an Infinite Fluid Domain[J]. International Journal for Numerical Methods in Engineering, 2017, 110: 163-185 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Maeda Y, Futamura Y, Sakurai T. Stochastic Estimation Method of Eigenvalue Density for Nonlinear Eigenvalue Problem on the Complex Plane[J]. JSIAM Letters, 2011(3): 61-64 [Article] [CrossRef] [Google Scholar]
- Kirkup S, Wu S F. The Boundary Element Method in Acoustics[J]. International Journal for Numerical Methods in Engineering, 2000, 108(5): 1973-1974 [Article] [Google Scholar]
- Canino L F, Ottusch J J, Stalzer M A, et al. Numerical Solution of the Helmholtz Equation in 2D and 3D Using a High-Order Nyström Discretization[J]. Journal of Computational Physics, 1998, 146(2): 627-663 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Rong J, Wen L, Xiao J. Efficiency Improvement of the Polar Coordinate Transformation for Evaluating BEM Singular Integrals on Curved Elements[J]. Engineering Analysis with Boundary Elements, 2014, 38: 83-93 [Article] [CrossRef] [Google Scholar]
- Gohberg I, Rodman L. Analytic Matrix Functions with Prescribed Local Data[J]. Journal D'analyse Mathématique, 1981, 40(1): 90-128 [Article] [CrossRef] [Google Scholar]
- Bai Z, Fahey G, Golub G. Some Large-Scale Matrix Computation Problems[J]. Journal of Computational & Applied Mathematics, 1996, 74(1/2): 71-89 [Article] [CrossRef] [Google Scholar]
- Hutchinson M F. A Stochastic Estimator of the Trace of the Influence Matrix for Laplacian Smoothing Splines[J]. Communication in Statistics-Simulation and Computation, 1989, 19(19): 432-450 [Article] [Google Scholar]
- Austin A P, Kravanja P, Trefethen L N. Numerical Algorithms Based on Analytic Function Values at Roots of Unity[J]. SIAM Journal on Numerical Analysis, 2014, 52(4): 1795-1821 [Article] [CrossRef] [Google Scholar]
- Chaillat S, Bonnet M. Recent Advances on the Fast Multipole Accelerated Boundary Element Method for 3D Time-Harmonic Elastodynamics[J]. Wave Motion, 2013, 50(7): 1090-1104 [Article] [CrossRef] [Google Scholar]
- Qu Shen, Chen Haoran. Eigenvalue Analysis for Acoustical Cavity Covered with Porous Materials by Using the Radial Integration Boundary Element Method[J]. Chinese Journal of Computational Mechanics, 2015, 32(1): 123-128 (in Chinese) [Article] [Google Scholar]
- Gao H, Matsumoto T, Takahashi T, et al. Eigenvalue Analysis for Acoustic Problem in 3D by Boundary Element Method with the Block Sakurai-Sugiura Method[J]. Engineering Analysis with Boundary Elements, 2013, 37(6): 914-923 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 振荡最剧烈核函数及其导数的Cauchy插值误差随插值项数变化规律 |
| In the text | |
 |
图2 复平面内T′(z)的Cauchy插值误差 |
| In the text | |
 |
图3 3个基准模型最大Cauchy插值误差 |
| In the text | |
 |
图4 汽车驾驶室内声腔BEM模型 |
| In the text | |
 |
图5 汽车驾驶室内声腔模型最大Cauchy插值误差 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


