EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 41 / No 6 (Decembre 2023) JNWPU, 41 6 (2023) 1073-1079 Full HTML
Open Access
Issue
JNWPU
Volume 41, Number 6, Decembre 2023
Page(s) 1073 - 1079
DOI https://doi.org/10.1051/jnwpu/20234161073
Published online 26 February 2024

© 2023 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

具有机动能力的再入飞行器具有提升突防效能、提高命中精度的优势, 因而成为飞行器再入技术的重要研究方向。在各种再入机动飞行器设计中, 最简单经济的方案之一就是采用一维滚动控制的固定配平飞行器[1]。

固定配平飞行器是利用飞行器外形不对称或质心偏移产生不可控的配平攻角, 通过滚转单通道控制改变配平升力的方向, 实现再入机动飞行。但这种单通道控制特性给制导带来了很大困难, 缺少合适的制导方法是制约这种不对称再入体多约束条件下落点精确控制的主要瓶颈。

目前国内外针对这类飞行器含约束条件下实现精确打击的制导律研究文献较少, 这种外形的应用也多集中在航天器返回等终端约束要求不高的情况。传统的弹道-升力式返回航天器再入过程以纵向多约束制导为主, 侧向采用速度倾侧角正负切换的方式控制横程偏差, 但这种方法在顾及飞行器姿控稳定性和可实现性条件下难以获得较高的落点精度。美国MK500机动弹头则采用程序飞行方式, 以牺牲精度换取机动能力[2]。Gracey等[3]针对固定配平攻角飞行器的特点提出了滚转制导律, 有效实现了固定配平飞行器的精确制导并解决了多余升力消耗问题, 但是难以在制导律中处理各项约束条件。文献[4]在滚转制导律基础上通过引入具有一定运动规律的虚拟目标作为引导, 实现了在不改变制导律形式情况下对落角的有效控制, 但这与满足再入过程的多约束条件还有一定距离。

针对固定配平攻角飞行器多约束条件下再入精确制导问题, 本文提出将轨迹优化和滚转制导律相结合, 利用高斯伪谱法收敛速度快、精度高的特点实现标准轨迹的快速优化, 满足多约束条件, 然后采用滚转制导律+虚拟目标的方式实现对标准轨迹的跟踪, 解决精确制导问题。

1 固定配平飞行器再入制导问题

1.1 固定配平飞行器模型

固定配平飞行器具有以下特点:

1) 俯仰、偏航通道通过配置适当静稳定度实现自稳定, 不施加控制;

2) 稳定飞行条件下, 飞行器攻角为固定配平攻角α=α*, 侧滑角为β=0;

3) 仅通过滚动控制改变γV实现机动飞行即可实现对弹道的控制。

假设地球模型为均匀球体, 固定配平飞行器再入制导模型为

式中, 各状态变量为[V, θ, ψV, x, y, z]T, 各元素依次为飞行器速度、弹道倾角、弹道偏角和飞行器在再入系下的位置坐标; 控制量为速度倾侧角γV; D, L分别为弹体所受阻力和升力; (gx, gy, gz)T为引力加速度在弹道系下的投影; (fx, fy, fz)T为地球自转引起的惯性加速度和哥式加速度在弹道系的投影。

1.2 再入制导约束条件

作为对地打击武器的再入机动飞行器, 再入制导问题需要考虑以下几类约束:

1) 过程约束

从结构安全和热防护角度出发, 再入飞行器通常对动压和过载的上限提出要求, 即

2) 终端约束

为了保证精度, 应满足严格的落点位置约束。以再入系中的坐标来描述, 期望落点的位置可以根据目标射程推算。

为了保证攻击效果、提高突防能力, 通常对终端落角和落速提出要求, 终端时刻自由, 即

式中, 落角约束应以当地弹道倾角为准, 为了简便可以根据目标射程, 针对地球曲率造成的倾角偏差值对落角约束指标进行修正。

3) 初始状态约束

初始状态固定为指定的再入条件

1.3 固定配平飞行器再入制导面临的困难

1) 制导指令的实现

经典的制导设计方法通常将三维制导问题分解为纵、侧向2个平面的二维制导问题，分别设计制导律, 进而会得到纵向和侧向2个方向的过载指令。采用STT或BTT控制的飞行器可以分别按直角坐标和极坐标方式实现2个方向的过载指令。然而固定配平攻角飞行器由于升力大小不可控, 只能控制升力方向, 无法同时满足上述2个维度制导指令。

2) 过剩升力的消耗

由于飞行器配平攻角不可控, 无法实现零升力弹道, 在升力过剩时需要有适当的制导律来消耗多余的升力[5]。

3) 再入过程的多约束条件

再入过程需要满足的终端约束、过程约束和控制约束条件是再入制导的典型问题, 进一步增大了固定配平飞行器制导律的设计难度。

因此实现固定配平飞行器多约束条件下精确打击, 就要求制导律同时解决上述3个问题。本文认为, 多约束问题可以通过轨迹优化有效解决, 而前2个问题则在轨迹跟踪时予以解决。

2 基于高斯伪谱法的标准轨迹优化

2.1 再入制导问题

取状态变量x(t)=[V, θ, ψV, x, y, z]T, 控制变量为u(t)=γV。为了提高突防效果, 选取落速最大为性能指标

为了使高斯伪谱法解算方便, 可对动力学方程进行无量纲化处理。

固定配平飞行器再入轨迹优化[6]可归纳为: 满足微分方程约束(1)和1.2节所述各终端约束、过程约束的Mayer型最优控制问题

2.2 高斯伪谱法求解

高斯伪谱法是将状态变量和控制变量在一系列LG点上离散, 并以离散点为节点构造Lagrange插值多项式来逼近状态变量和控制变量, 从而将连续的最优控制问题转化为具有一系列代数约束的有限维非线性规划(NLP)问题。

按照高斯伪谱法求解的常规步骤[7], 最优控制问题(7)可离散为在N个LG点τk(k=1, 2, …, N)和1个初始点τ0=-1共N+1个离散节点上, 寻求状态变量 X(τk)、控制量U(τk)和终端时刻tf, 使性能指标(8)最小, 并满足动力学方程约束(9)、边界条件约束(10)和过程约束(11)的非线性优化问题。

式中, D∈RN×(N+1)为微分近似矩阵。

本文采用成熟的序列二次规划(SQP)方法求解标准轨迹优化的NLP问题。

3 标准轨迹的跟踪

3.1 固定配平飞行器的标准轨迹跟踪问题

对于固定配平飞行器, 经典的标准轨迹跟踪方法以和约束指标直接相关的纵向制导为主, 例如采用如(12)式所示的跟踪制导律

式中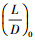：为标准轨道升阻比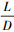；为飞行器配平升阻比；h, R分别为飞行高度、纵程。而侧向制导通过设置漏斗形的横程边界，改变γV的正负，减小横程偏差。

这种制导律倾侧角指令是开关式的不连续信号, 在接近目标时倾侧角正负切换的频率变高。这种快速的滚动与频繁的方向切换不仅对飞行稳定性不利, 也对控制系统提出了过高的要求。在滚转速度受限情况下会造成较大的落点偏差。因此这种方法仅适用于精度要求不高的场合。

为了实现对标准轨迹的有效跟踪, 并获得较高的制导精度, 本文采用针对固定配平飞行器设计的滚转制导方法, 通过设置虚拟目标实现对标准轨迹的跟踪。

3.2 滚转制导律

如图 1所示, O为飞行器质点, T为目标质点, Oxyz为弹道坐标系。定义飞行器速度矢量V和弹目视线构成的平面为误差平面, 同时定义速度矢量与弹目视线的夹角为误差角η(0°≤η≤180°)。为方便描述, 定义误差系Ox′y′z′, 其中Ox′与速度矢量重合, Oy′轴在误差平面内, 指向弹目视线一侧。记误差平面和弹道坐标系Oxy平面的夹角为ξ, 顺着Ox方向看, Oy顺时针转动到Oy′时为正; 飞行器配平升力L与弹道坐标系Oxy平面的夹角即为倾侧角γV。根据定义，ξ和γV均在Oyz平面内。

进而可得到三自由度相对运动方程组如(13)式所示, 其中前2个方程描述了误差平面内的相对运动关系, 第三个方程描述了误差平面的旋转。

式中

滚转制导律的思想是使误差平面内的弹目距离r和误差角η收敛到0, 而误差平面的旋转角度ξ不影响r和η的收敛, 因此可以不施加控制。

在误差平面内建立滚转制导律的制导方程为

式中, K为制导系数, 取值应满足K>1。有关证明可参考文献[5]。进而可得到滚转制导律的制导指令表达式为

式中

thumbnail 图1

滚转制导示意图

3.3 基于虚拟目标的标准轨迹跟踪

令虚拟目标沿优化得到的标准轨迹运动, 飞行器按照滚转制导律对其进行跟踪。虚拟目标取为标准轨迹上飞行器前方纵程相距ΔS处, 即任意时刻可根据飞行器当前纵程S和ΔS在标准轨迹上插值得到其位置坐标。

当虚拟目标与真实目标(标准轨迹落点)重合后不再继续运动, 之后再入飞行末段退化为简单的打击固定目标的滚转制导。

3.4 制导方法稳定性

在不考虑目标运动时, 可以证明[5], 在等式(15)的约束下(对应飞行器升力L对误差角η的控制能力不小于自由运动对误差角的影响), 当K>1时, 可有效控制误差角η趋于0。

当飞行器接近虚拟目标时, 弹目视线距离r较小, (15)式不成立, 此时飞行器因机动能力不足导致制导律不收敛, 并最终产生制导方法误差。为了减小该影响, 保证较高制导精度, 应在虚拟目标设置时, 避免ΔS过小触发上述条件; 另一方面在末段虚拟目标与标准轨迹落点重合后, 可通过设计合理的制导系数与飞行速度, 减小进入不收敛的时间。

考虑虚拟目标速度情况下, 制导律稳定性分析可参考文献[4], 经证明有上文类似结论, 即在飞行器机动能力足够抵消误差影响时, 误差角可收敛至0, 并实现飞行器与虚拟目标呈尾追状态。

本文采用滚转制导律跟踪虚拟目标时, 假设虚拟目标每一时刻都是静止的, 因此制导律中未显式包含虚拟目标的速度项, 这使得在标准轨迹上插值确定虚拟目标位置时, 避免了获取其速度的额外处理, 该方法在不影响制导律稳定性基础上, 有利于工程实现[8]。当虚拟目标与标准轨迹落点重合后问题完全转化为滚转制导律稳定性问题。

4 仿真验证与调参分析

以下通过三自由度仿真对本文提出的制导方法进行仿真验证。

假设飞行器姿态保持配平攻角α=5°, 配平侧滑角β=0°。初始条件和约束指标见表 1。

表1

初始条件和约束指标

4.1 标准轨迹优化

取节点个数N=25进行高斯伪谱法轨迹优化, 优化结果如图 2所示。

1) 优化所得的标准轨迹主要指标为落速1 154 m/s, 落角-72.7°, 轴向最大过载30.6g, 法向最大过载33.4g, 最大动压2.15 MPa, 均能满足约束条件。

2) 飞行器通过平缓变化的倾侧角指令实现了纵向平面弹道在约30 km高度处的拉起减速及低空段的高抛弹道, 满足了过程约束和终端约束要求, 倾侧角指令变化速度不超过15°/s。

3) 倾侧角曲线显示优化后的标准轨迹仍是通过正反2个方向的滚转实现多余升力的消耗, 但优化后的滚转指令远比传统方法更容易跟踪实现。

thumbnail 图2

标准轨迹弹道曲线

4.2 轨迹跟踪

采用“虚拟目标+滚转制导律”的方法对以上优化所得的标准轨迹进行跟踪。取滚转制导律制导系数为K=1.4, 虚拟目标位于飞行器前方纵程相距ΔS=49 km的标准轨迹上。部分仿真结果如图 3所示。

根据仿真结果可得以下结论:

1) 使用滚转制导律可以比较有效地实现对标称轨迹的跟踪, 在滚转限速条件下, 实际弹道主要指标为落速1 236.5 m/s, 落角-59.6°, 轴向最大过载31.5g, 法向最大过载33.3g, 最大动压2.18 MPa, 各指标参数与标称轨迹接近。实际弹道落点偏差为29 m, 这对于机动能力有限的固定配平攻角再入飞行器来说是合理的。

2) 使用滚转制导律虽然可以使各指标参数与标准轨迹接近, 但仍存在一定偏差, 难以实现实际弹道对标称轨迹的精确跟踪。这是因为固定配平攻角飞行器升力机动控制能力有限, 采用的滚转制导律具有如下特点: 在机动能力不足时产生跟踪误差, 在机动能力过剩时以螺旋接近方式消耗多余升力。再入过程中滚转制导律的上述制导效果将体现在实际弹道中, 进而必然和标准轨迹产生差异。尤其是在飞行末段, 虚拟目标和实际目标重合后, 跟踪标准轨迹问题已退化为打击固定目标的滚转制导, 弹道明显体现出滚转制导律的特点, 与标准轨迹无关。此时飞行器已经过动压和过载峰值点, 因此这种退化一般不影响过程约束的满足情况, 但弹道倾角会由于螺旋接近方式出现小幅振荡(见图 4)。

3) 考虑到滚转制导律对标准轨迹的上述跟踪误差, 以及参数拉偏条件下的制导偏差, 轨迹优化时设置的约束指标应该比给定的约束条件更加严格, 以预留足够的裕度。

在轨迹跟踪时, 虚拟目标位置ΔS、制导系数K和滚转角速度限幅大小均会对落点精度和约束指标产生显著影响, 大量仿真显示, 制导参数影响有以下规律:

1) 在正常跟踪情况下, 过载、动压约束基本与标准轨迹一致, 制导参数变化影响较小(1%以内)。

2) 虚拟目标位置ΔS的设置是实现轨迹跟踪最关键的参数, 对落点偏差和落速(落角)都有显著影响。不同ΔS条件下仿真结果统计如表 2。

表2

ΔS取值对主要指标的影响

可见, 在一定范围内, ΔS取值越大, 落点精度提高, 同时落速减小, 反之亦然。超出该范围后, 继续增大ΔS并不能继续提高精度, 而落速仍会快速降低, 这是由滚转速度受限情况下滚转制导律自身的方法误差造成的。同样, ΔS取值过小并不能继续提高落速, 而精度则会快速下降, 这是由过程约束和标准轨迹限制造成的。因此应综合考虑精度和落速的要求选择适当的ΔS值。

3) 制导系数K的影响与滚转制导律影响规律一致。即随着K增大, 最大滚转角速度增大, 落点精度在一定范围内有所提高, 受限于滚转制导律方法误差, 继续增大K落点精度不会继续提高。因此K的取值可根据滚转制导律本身的要求进行设计。

4) ΔS的最优取值与制导系数K大小有关。仿真显示, 在精度、落速、落角指标接近情况下, 若K=1.4, ΔS=49 km, 而K=1.6时ΔS应取35 km, K=1.8时ΔS应取19 km。因此制导律设计时应首先针对滚转制导律确定适当的K值, 在此基础上优化调整ΔS。

5) 与滚转制导律影响规律一致, 滚转角速度增大有助于提高落点精度。但滚转速度过快会使姿态运动的稳定性变差, 并且滚转控制系统难以实现, 因此应根据飞行器姿控能力对滚转速度进行适当限幅。

6) ΔS的取值也可以根据需要设计成时变参数, 在不同的飞行阶段, 或者不同飞行状态下, 利用ΔS的变化, 兼顾落速、精度等不同指标的要求。

thumbnail 图3

三维弹道曲线
thumbnail 图4

当地弹道倾角变化曲线

5 结论

本文采用“高斯伪谱法轨迹优化+滚转制导律跟踪标准轨迹”的方法, 解决了固定配平攻角飞行器多约束条件下再入精确制导问题。仿真结果显示, 该方法可有效解决再入过程的各项终端约束、过程约束问题, 并获得满意的落点精度。同时该方法除了依靠轨迹优化满足约束条件外, 采用滚转制导律跟踪标准轨迹时, 虚拟目标的设置也会对最终的精度和落速产生影响。根据仿真分析总结, 该制导方法在设计和参数设置时, 有以下规律:

1) 因固定配平攻角飞行器升力机动控制能力有限, 实际跟踪弹道会与轨迹优化所得标准轨迹存在跟踪偏差, 采用高斯伪谱法进行轨迹优化时, 设置的约束指标应该比给定的约束条件更加严格, 以预留足够的裕度。

2) 制导律设计时应首先确定适当的制导系数K值, K的影响与滚转制导律影响规律一致, 可根据滚转制导律本身的要求进行设计。在满足滚转制导律稳定性前提下, K增大, 落点精度在一定范围内有所提高, 但继续增大K落点精度不会继续提高, 同时考虑到工程实际中最大滚转角速度的限制, K的取值不宜过大, 必要时根据飞行器姿控能力对滚转速度进行适当限幅。

3) K值确定后, 可在此基础上确定虚拟目标位置ΔS。在一定范围内, ΔS取值越大, 落点精度提高, 同时落速减小, 反之亦然。超出该范围后, 继续增大ΔS并不能继续提高精度, 而落速仍会快速降低。同样, ΔS取值过小并不能继续提高落速, 而精度则会快速下降。因此需根据实际情况, 综合考虑精度和落速的要求, 通过仿真等手段对ΔS取值进行参数优选。更精细的设计中, 可将ΔS取为时变参数, 在不同的飞行阶段利用ΔS的变化, 更好地兼顾各项约束指标。

4) ΔS的最优取值与制导系数K大小有关, 若K有调整, 虚拟目标位置ΔS也应相应优化。K越大, 在实现相近的指标时, ΔS应设置得越小。

References

  1. WANG Yafei, YU Jianqiao, MEI Yuesong, et al. Nonlinear dynamics of fixed-trim reentry vehicles with moving-mass roll control system[J]. Journal of Systems Engineering and Electronics, 2016, 27(6): 1249–1261 [Article] [CrossRef] [Google Scholar]
  2. ZHOU Min, ZHOU Jun, LU Mingfei. A spiral-maneuver control method for a fixed-trim warhead[J]. Journal of Astronautics, 2017, 38(11): 1195–1203 [Article] (in Chinese) [Google Scholar]
  3. GRACEY C, CLIFF E M, LUTZE F H, et al. Fixed-trim reentry guidance analysis[C]//AIAA Guidance and Control Conference, Albuquerque, United States, 1981 [Google Scholar]
  4. GENG Keda, ZHOU Jun, LIN Peng. Design of rolling-guidance law using virtual target with control of terminal azimuth for afixed-trim vehicle[J]. Journal of Solid Rocket Technology, 2015, 38(3): 320–325 (in Chinese) [Google Scholar]
  5. LI Zixing, LI Gaofeng, HUANG Ruiling. A vehicle rolling-guidance law based on fixed trimmed angle of attack[J]. Aerospace Control and Application, 2012, 38(6): 23–26 (in Chinese) [Google Scholar]
  6. ROBERT T B, DAVID S R. Trajectory optimization for a fixed-trim reentry vehicle using direct collocation and nonlinear programming[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, 2000: 14–17 [Google Scholar]
  7. ZHOU Liang, WANG Haoyu, SHANG Haibin, et al. Research on optimal design of the glide trajectory of space-based reentry vehicle based on Gaussian pseudo spectral method[J]. Air & Space Defense, 2020, 3(3): 89–95 (in Chinese) [Google Scholar]
  8. LI Guanlin, CHAO Tao, WANG, Songyan, et al. Guidance law for fixed-trim vehicle against maneuvering target[J]. Systems Engineering and Electronics, 2019, 41(3): 611–618 (in Chinese) [Google Scholar]

All Tables

表1

初始条件和约束指标

In the text
表2

ΔS取值对主要指标的影响

In the text

All Figures

thumbnail 图1

滚转制导示意图
In the text
thumbnail 图2

标准轨迹弹道曲线
In the text
thumbnail 图3

三维弹道曲线
In the text
thumbnail 图4

当地弹道倾角变化曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.