| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1257 - 1265 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861257 | |
| Published online | 02 February 2021 | |
Cooperative Intercepting Guidance Law for Large Maneuvering Target with Impact Angle Constraint
带有攻击角约束的大机动目标协同攻击制导律
1
China Airborne Missile Academy, Luoyang 471009, China
2
Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471009, China
3
Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China
4
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
Received:
14
May
2020
A distributed multi-missile cooperative guidance law based on the finite time theory is proposed to solve the terminal guidance problem of three-dimensional multi-missiles cooperative interception of large maneuvering target. According to the finite time consistency theory, an adaptive guidance law based on the integral sliding mode is designed to ensure that all missiles can reach the target at the same time in the terminal guidance process. The longitudinal and lateral acceleration of the line of sight are based on the guidance law of the fast terminal sliding mode surface. The terminal attack angle is constrained, so that the terminal attack Angle can reach the expected value in finite time. The simulation results show that the designed guidance law can achieve the cooperative attack on the maneuvering targets.
摘要
针对三维空间内多枚空空导弹协同攻击高速大机动目标末制导问题,提出了一种分布式有限时间协同制导律设计方法。视线方向加速度根据有限时间一致性理论设计了基于积分滑模面的自适应制导律,保证了在末制导过程所有导弹能够同时达到目标;视线纵向和视线侧向的加速度均采用基于快速终端滑模面的制导律,同时对末端攻击角进行约束,使得末端攻击角能够在有限时间达到期望值。仿真算例验证了所提出的制导律能够实现对机动目标的协同攻击。
Key words: three-dimension / coordination guidance / maneuvering target / impact angle constraint
关键字 : 三维空间 / 协同制导 / 机动目标 / 攻击角约束
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
现代战争正在由信息化时代向着智能化时代转变,空空导弹作为空中战场的核心武器,其性能和制导技术在空战中有着至关重要的作用[1]。美国为了夺取军事优势,构建了“网络中心战”作战体系,并不断地完善,朝着“分布式作战”、“决策中心战”等新的方向转变。在转变的过程中美国提出了大量的新技术和新装备,以提高作战能力,进一步加强作战优势,战场中出现了新环境和新目标。随着新型干扰的出现,空战环境的变得更为复杂。空中目标性能的提高,数量和种类的增多,对空空导弹的性能提出了新的更高的要求。
传统空空导弹作战都是单对单的,导弹在平台或者体系的信息支援下获取目标信息,通过自身的制导控制系统,完成对于目标的精确打击。为了适应未来智能化战争的新需求,采用多枚空空导弹协同攻击,构建智能化制空作战的空空导弹群体,能够大大提高反隐身,抗干扰等制空作战能力。空空导弹协同制导已经成为目前研究的新方向。
在空空导弹协同制导问题[2]中,要求获得最小的脱靶量[3],同时满足导弹的末端攻击角、碰撞时间等末端约束条件[4]。控制末端攻击角能够有效提高战斗部杀伤能力,而通过导弹间通信拓扑使得碰撞时间相同,可实现饱和攻击[5];协同制导技术作为协同攻击中的核心技术,在协同作战中起着至关重要的作用,因此对导弹协同制导的研究具有非常重要的意义[6-8]。
近年来,在协同制导技术研究方面,各国学者提出了许多先进的制导律设计方法,包括最小时间控制、最小能量控制、冲击时间控制和冲击角控制等[9-11]。对于单枚导弹,上述方法已经达到较高的精度。而对于空中大机动目标的制导问题,采用多枚导弹协同制导,能够达到更好的攻击效果。然而,由于初始条件的不同和各导弹之间的通信限制,对机动目标的同时攻击更加困难[12]。
在现有文献中,很多学者提出了不同典型方法来研究多枚导弹的协同制导问题。具有代表性的一类是将剩余时间作为协调变量的攻击时间协同的制导律,如文献[13]中设计了线性系统的攻击时间约束的闭环制导律,它可以导引多枚导弹在适当时间同时攻击静止目标。文献[14]提出了时间约束条件的扩展,同时控制了攻击时间和攻击角度。对于上述2种方法,需要对每枚导弹进行剩余时间控制。为了提高攻击时间约束的制导律性能,文献[15]提出了基于通信协议的分布式二维协同制导模型,根据一致性理论设计了协同制导律。
另一类方法是,采用“领弹-从弹”模型来描述多导弹协同制导。如文献[16]在传统比例导引的基础上,提出了一种“领弹-从弹”策略来实现多枚导弹的协同攻击,将领弹的剩余距离和弹道偏角误差作为参考状态变量。文献[17]则提出设置1枚虚拟领弹,从而把时间约束转换为非线性化跟踪问题。文献[18]设计了反馈线性化的协同制导律,使每个从弹的攻击时间都能够在有限时间内收敛。
文献[19]采用剩余时间估计方法,提出了一种角度约束的制导律来实现在指定时间内的截获,是一种用于三维场景中分布式导引律。文献[20]提出一种基于扩展比例导引制导律的协同策略,使得低速拦截器对高速目标实施齐射攻击。这些都是解决三维作战中运动目标协同制导问题的初步尝试。
综上,目前的研究中,大多只考虑了二维平面,设计了二维平面内的多导弹协同制导律。在三维作战中,协同制导策略情况较为复杂,对于三维空间内的多导弹同时攻击高速大机动目标的分布式协同制导律较为少见。
针对上述问题,本文重点研究了多导弹协同的三维制导律,提出了一种针对三维空间内高速大机动目标的协同制导律。其中,视线方向对文献[13]中的剩余时间给出了三维情况下的表达式,将其作为协调变量加入协同制导模型,并根据有限时间理论设计了视线方向的制导律。将视线法向分为侧向和纵向,在这2个平面分别采用了快速趋近律来设计快速终端滑模制导律,并对末端期望的弹道倾角和弹道偏角进行约束。最后将本文提出的方法进行仿真分析,验证了本文方法的有效性和合理性。
1 模型建立
图 1为三维空间制导示意图, 其中导弹和目标的质心分别是M和T, 坐标系Mxyz与参考惯性坐标系平行, Mx4y4z4为视线坐标系, r为目标和导弹的相对距离,qε与qβ分别表示视线倾角和视线偏角[19, 21]。
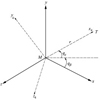 |
图1 三维空间弹目几何关系示意图 |
导弹与目标的相对速度矢量在视线系下的表达式为
对(1)式求导可得
式中:
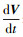 表示矢量V的绝对导数;
表示矢量V的绝对导数;
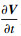 为矢量V的相对导数; ω为角速度。
为矢量V的相对导数; ω为角速度。
将向量ω进行叉乘转化为矩阵,形式如下所示:
结合(2)式和(3)式可得
因此得到三维制导模型下弹-目相对运动方程:
式中,aT=[aTraTεaTβ]T, aM=[aMεaMεaMβ]T是目标加速度的矢量和导弹加速度的矢量在视线坐标系下的投影。
规定状态变量为:x1=r, x2=, x3=qε-qεd, x4=ε, x5=qβ-qβd, x6=β其中, qεd, qβd分别为期望的终端视线倾角和终端视线偏角。结合方程(6)和(7), 可得到带有终端攻击角约束的三维制导系统状态方程如下[21]
引入n个导弹的末制导剩余时间tgoi
对(9)式求导可得
将末制导剩余时间tgoi作为三维空间协同制导模型的状态变量, 则弹目相对运动方程可以表示为[21]
令
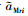 作为新的控制输入
作为新的控制输入
将(12)式代入状态方程(11)可以推出具有角度约束的三维协同制导模型[21]
2 制导律设计
由(13)式可知, 系统的协同制导律设计是由两部分组成的:一方面, 外界存在干扰的情况下, 设计新的视线方向加速度指令
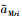 从而使得多导弹协同制导系统的各个导弹的末制导剩余时间tgoi能够在有限时间内趋于一致; 另一方面设计视线纵向和视线侧向的加速度aεi和aβi能够满足有限时间达到收敛。
从而使得多导弹协同制导系统的各个导弹的末制导剩余时间tgoi能够在有限时间内趋于一致; 另一方面设计视线纵向和视线侧向的加速度aεi和aβi能够满足有限时间达到收敛。
2.1 视线方向制导律设计
变量tfi指单枚导弹在t时刻预测的能够攻击目标的时间, 可得[22]
由(14)式可得, 要使tgoi趋于一致, 只需使得tfi趋于一致。
根据(13)式可得
选取积分滑模面
式中:tfi(0)是tfi的初始值;uinorm是一致性协议, 其表达式为[21]
根据文中采用的积分滑模面和三维制导模型(13)提出基于有限时间的一致性协议
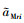 。
。
定理1 对于制导系统(13), 当其通信拓扑图G无向并连通, 设计一致性协议[21]
式中:
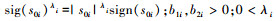
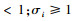 。
。
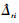 是Δri的估计值, 自适应律如下[21]
是Δri的估计值, 自适应律如下[21]
可以保证滑模面s0在控制器(17)式作用下能够在有限时间内收敛到滑模面s0→0。协同制导系统中tfi能够在有限时间趋于一致, 同理剩余时间tgoi也能够趋于一致。
证明 根据(17)式对s0求导可知
令
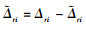 , 取Lyapunov函数
, 取Lyapunov函数
考虑(19)式和(20)式, 并对(21)式相对时间求导, 可得[21]
由(22)式得
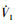 为半负定, 说明V1是非增函数并且有界, 因此,
为半负定, 说明V1是非增函数并且有界, 因此,
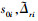 也有界。
也有界。
构造Lyapunov函数为
对(23)式求导
由(24)式可知
 , 则
, 则
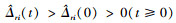 , 当
, 当
 足够大且σi满足
足够大且σi满足
又
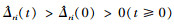 , 则
, 则
根据(26)式可得
因此, 有限时间内s0i=0, 可以确定当滑模面收敛到0时,
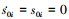 , 此时攻击时间tfi和剩余时间tgoi都能够在有限时间保持一致, 证毕。
, 此时攻击时间tfi和剩余时间tgoi都能够在有限时间保持一致, 证毕。
2.2 视线纵向制导律设计
选择非线性快速终端滑模面
式中:
选取幂次趋近律如下
对滑模面(28)式求导可得
由(29)式和(30)式得
将(8) 式中
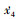 方程带入(31)式可得
方程带入(31)式可得
(32) 式中含有sigγ1(s1)为变结构项, 该制导律为滑模变结构控制, 鲁棒性强。
根据上述分析, 给出末端攻击角约束的有限时间收敛的快速终端滑模的视线方向制导律, 即定理2。
定理2 对于制导系统(13)式, 选取滑模面(28)式和趋近律(29)式, 所设计的制导律如(32)式所示。
证明 选取Lyapunov函数为
对(33)式求导可得
将(28)式和(29)式代入(34)式可得
由于
即
所以
由于制导阶段x1>0, ρ1>0, 因此
故系统状态可以到达滑模面。
根据(39)式可知
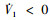 , 进而可知V1(t)有界。由Lyapunov稳定性理论可知, 系统渐进稳定, 滑模面s1能够在有限时间收敛为0。
, 进而可知V1(t)有界。由Lyapunov稳定性理论可知, 系统渐进稳定, 滑模面s1能够在有限时间收敛为0。
系统状态沿滑模面运动时已达到收敛, 此时系统状态为
此时状态方程可表示为
选取Lyapunov函数为
对(42)式求导可得
将(41)式代入(43)式得
根据(44)式可知
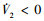 , 进而可知V2(t)有界, 系统状态x3在有限时间收敛到一定区域。
, 进而可知V2(t)有界, 系统状态x3在有限时间收敛到一定区域。
进一步可以得到
从(45)式可得, 系统状态x4在有限时间收敛到一定区域。
由Lyapunov稳定性理论可知, 系统渐进稳定, 当t→∞时, x3→0。
由(46)式可得, 系统末端视线角最终收敛到qεd。至此, 定理证毕。
然而, 变结构项会引起系统的抖振问题, 使得导弹的过载产生震荡现象, 因此本文采用饱和函数代替制导律中的变结构项。下面给出饱和函数[21]
式中, k=const>0是一个非常小的值。可以看出, 当|s1|>k时, sat(s1)=sign(s1)因此用饱和函数代替符号函数后的制导律不影响收敛效果。
2.3 视线侧向制导律设计
选择非线性快速终端滑模面
式中
选取幂次趋近律如下
对滑模面(48)式求导可得
由(48)式和(49)式得
将(8)式中
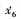 方程带入(51)式可得
方程带入(51)式可得
根据上面的分析, 给出定理3。
定理3 对于制导系统(13)式, 选取滑模面(48)式和趋近律(49)式所设计的制导律如(52)式所示。
证明 选取Lyapunov函数为
对(53)式求导可得
将(48)式和(49)式代入(54)式可得
由于
即
所以
由于制导阶段x2>0, ρ2>0, 因此
故系统状态可以到达滑模面。
系统状态沿滑模面运动至收敛, 此时系统状态为
此时状态方程可表示为
选取Lyapunov函数为
对(62)式求导可得
将(61)式代入(63)式得
根据(64)式可知
 , 进而可知V2(t)有界, 系统状态x5在有限时间收敛到一定区域。
, 进而可知V2(t)有界, 系统状态x5在有限时间收敛到一定区域。
进一步可以得到
从(65)式可得, 系统状态x6在有限时间收敛到一定区域。
由Lyapunov稳定性理论可知, 系统渐进稳定, 当t→∞时, x5→0, 即
由(66)式可得, 系统末端视线角最终收敛到qβd。至此, 定理证毕。
3 仿真分析
为了验证本文提出的协同制导算法, 设计了3枚导弹协同攻击高速大机动运动目标的作战场景, 仿真条件设置如下:
末制导初始时刻, 导弹和目标的参数如表 1所示。各导弹提供的视线方向最大加速度为25g, 视线纵向和侧向最大加速度均为50g, 目标在视线侧向和视线纵向机动加速度分别机动为:aTε=10g, aTβ=10g, 仿真步长0.001 s。导引头盲区:r0=50 m, 3枚导弹之间的通讯网络为中c=[0, 1, 1;1, 0, 1;1, 1, 0](该矩阵表示在末制导过程中, 各个导弹之间的通讯关系)。
导弹和目标的初始条件及各弹期望视线角
制导律仿真参数如下:
视线方向:θi=0.5, σi=1.5, b1i=6, λi=0.6, b2i=2。
视线纵向:k1=0.5, k2=0.6, k3=0.5, α1=1/3, γ1=0.05, ρ1=5。
视线侧向:l1=0.5, l2=0.6, l3=0.5, α2=1/3, γ2=0.05, ρ2=5。
根据上述仿真条件与仿真参数,仿真结果如所图 2~图 7所示。由图 2至图 4可以看出,针对高速大机动运动目标,本文的三维协同制导律中,3枚导弹几乎在同一时间内到达目标。此外,根据图 4可知,在文中给出的有限时间一致性协议下,3枚导弹的末制导剩余时间能够在大约3 s趋于一致。图 5表明了各导弹的在视线方向的加速度在合理范围内,初始阶段波动较大是为了能够调整导弹的末制导剩余时间使得同时攻击机动目标。图 6和图 7分别表明3枚导弹在视线纵向和视线侧向上的加速度,在制导过程开始时该值较大,其原因是保证视线角速率可以收敛到零,随着视线角速率收敛后加速度曲线逐渐平缓。因此,根据仿真结果可以看出,本文所设计的有限时间滑模导引律针对高速大机动目标具有很好的适应性和有效性。
 |
图2 目标和导弹轨迹示意图 |
 |
图3 导弹和目标的相对距离 |
 |
图4 剩余时间 |
 |
图5 视线方向过载 |
 |
图6 视线纵向过载 |
 |
图7 视线侧向过载 |
另外,表 2给出了各枚导弹击中目标时的脱靶量与攻击时间。从表中可以看到,本文提出的协同制导律所产生的导弹的脱靶量较小且能够保证同时攻击。
脱靶量和制导时间
4 结论
本文提出了三维空间内多枚空空导弹针对高速大机动目标攻击角约束的协同制导律。主要研究成果包括:
1) 建立了考虑剩余时间和攻击角度约束的三维协同制导模型。
2) 结合图论、自适应控制理论和有限时间收敛理论,设计视线方向的制导律使得3枚导弹可以同时攻击目标;视线纵向、视线侧向设计了攻击角度约束的导引律,使弹目视线角在有限时间收敛至期望值。
References
- Fan Huitao, Zhang Pengpeng. The Challenges for Air-to-Air Missile[J]. Aero Weaponry, 2017 (2): 3– 7 (in Chinese) [Google Scholar]
- Ren Miao, Wen Lin, Wang Xiuping. Research on Foreign Air-to-Air Missiles Development in 2017[J]. Aero Weaponry, 2018 (1): 62– 70 (in Chinese) [Google Scholar]
- Wei Mingying, Cui Zhengda, Li Yunqian. Review and Future Development of Multi-Missile Coordinated Interception[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41 (suppl 1): 29– 36 (in Chinese) [Google Scholar]
- Ma Peibei, Wang Xingliang, Ji Jun. Review of the Research on Cooperative Guidance of Multi-Missile Attack Time and Attack Angle[J]. Aerodynamic Missile Journal, 2018 (6) 67– 71 (in Chinese) [Google Scholar]
- Wang Jianqing, Li Fan, Zhao Jianhui, et al. Summary of Guidance Law Based on Cooperative Attack of Multi-Missile Method[J]. Flight Dynamics, 2011, 29 (4): 6– 10 (in Chinese) [Google Scholar]
- He S, Wang W, Wang J. Discrete-Time Super-Twisting Guidance Law with Actuator Faults Consideration[J]. Asian Journal of Control, 2017, 19 (6): 1– 8 [CrossRef] [Google Scholar]
- Guo Zhengyu, Han Zhiguo. Multi-Missile Cooperative Guidance Law Design Based on Fast Non-Singular Terminal Sliding Mode[J]. Aero Weaponry, 2020, 27 (3): 62– 66 (in Chinese) [Google Scholar]
- Liu Xiang, Liang Xiaogeng. Integrated Guidance and Control of Multiple Interceptors with Impact Angle Constraints Considered[J]. Journal of Northwestern Polytechnical University, 2019, 37 (2): 273– 282 (in Chinese) [CrossRef] [Google Scholar]
- Li G, Yan H, Ji H. A Guidance Law with Finite Time Convergence Considering Autopilot Dynamics and Uncertainties[J]. International Journal of Control, Automation and Systems, 2014, 12 (5): 1011– 1017 [CrossRef] [Google Scholar]
- Liu Lei, Gao Wenji, Wang Jianchao. Cooperative Terminal Guidance Analysis of Guided Rocket Missle Based on Gauss Pseudo-Spectral Method[J]. Missiles and Space Vehicles, 2020 (3): 81– 85 (in Chinese) [Google Scholar]
- He S, Wang W, Wang J. Adaptive Backstepping Impact Angle Control with Autopilot Dynamics and Acceleration Saturation Consideration[J]. International Journal of Robust and Nonlinear Control, 2017, 27 (17): 3777– 3793 [Google Scholar]
- Li B, Lin D, Wang H. Finite Time Convergence Cooperative Guidance Law Based on Graph Theory[J]. Optik-International Journal for Light and Electron Optics, 2016, 127 (21): 10180– 10188 [CrossRef] [Google Scholar]
- Jeon I, Lee J, Tahk M. Impact-Time-Control Guidance Law for Anti-Ship Missiles[J]. IEEE Trans on Control Systems Technology, 2006, 14 (2): 260– 266 [CrossRef] [Google Scholar]
- Lee J, Jeon I, Tahk M. Guidance Law to Control Impact Time and Angle[J]. IEEE Trans on Aerospace and Electronic System, 2007, 43 (1): 301– 310 [CrossRef] [Google Scholar]
- Zhou J, Yang J. Distributed Guidance Law Design for Cooperative Simultaneous Attacks with Multiple Missiles[J]. Journal of Guidance, Control, and Dynamics, 2016, 39 (10): 2436– 2444 [Google Scholar]
- Zhang Youan, Ma Guoxin, Wagn Xingping. Time-Cooperative Guidance for Multi-Missiles:A Leader-Follower Strategy[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30 (6): 1109– 1118 (in Chinese) [Google Scholar]
- Zhao S Y, Zhou R, Chen W. Design of Time-Constrained Guidance Laws via Virtual Leader Approach[J]. Chinese Journal of Aeronautics, 2010, 23 (1): 103– 108 [CrossRef] [Google Scholar]
- Zhang Y, Wang X, Ma G. Impact Time Control Guidance Law with Large Impact Angle Constraint[J]. Journal of Aerospace Engineering, 2015, 229 (11): 2119– 2131 [Google Scholar]
- Wang X, Lu X. Three-Dimensional Impact Angle Constrained Distributed Guidance Law Design for Cooperative Attacks[J]. ISA Transactions, 2018, 73: 79– 90 [CrossRef] [Google Scholar]
- Ghosh S, Ghose D, Raha S. Retro-PN Based Simultaneous Salvo Attack Against Higher Speed Nonmaneuvering Targets[J]. IFAC Proceedings Volumes, 2014, 47 (1): 34– 40 [CrossRef] [Google Scholar]
- Song Junhong. Research on Finite-Time Guidance Law and Cooperative Guidance Law of Multi-Missiles for Intercepting Maneuvering Target[D]. Harbin: Harbin Institute of Technology, 2018 (in Chinese) [Google Scholar]
- Lyu Teng, Lyu Yueyong, Li Chuanjiang, et al. Finite Time Cooperative Guidance Law for Multiple Missiles with Line-of-Sight Angle Constraint[J]. Acta Armamentarii, 2018, 39 (2): 305– 314 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 三维空间弹目几何关系示意图 |
| In the text | |
 |
图2 目标和导弹轨迹示意图 |
| In the text | |
 |
图3 导弹和目标的相对距离 |
| In the text | |
 |
图4 剩余时间 |
| In the text | |
 |
图5 视线方向过载 |
| In the text | |
 |
图6 视线纵向过载 |
| In the text | |
 |
图7 视线侧向过载 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


