| Issue |
JNWPU
Volume 37, Number 2, April 2019
|
|
|---|---|---|
| Page(s) | 273 - 282 | |
| DOI | https://doi.org/10.1051/jnwpu/20193720273 | |
| Published online | 05 August 2019 | |
Integrated Guidance and Control of Multiple Interceptors with Impact Angle Constraints Considered
攻击角约束多拦截弹协同制导控制一体化研究
School of Automation, Northwestern Polytechnical University, Xi’an 710072, China
Received:
13
March
2018
To solve the multi-interceptor coordination problem and to intercept the target with impact angle constraint, a novel distributed cooperative control algorithm with impact angle constraint based on integrated guidance and control is proposed. First, the mathematic model of integrated guidance and control is established by combining the interceptor-target relative motion model with the dynamic equation of the interceptor on pitch plane. The time varying gain extended state observer is developed to estimate and compensate the unknown disturbance. Based on the estimated value and fast nonsingular dynamic surface sliding control method, the IGC algorithm of leader is given; Then, based on distributed cooperative "leader-follower" model, the cooperative control strategy of multi-interceptor is designed, and gives out speeds in two directions on pitch plane, which are transformed to the command of total velocity and trajectory angle based on kinematic relations. Finally, to control the follower, the time varying gain extended state observer and the dynamic surface sliding control method are adopted. The simulation results demonstrate the effectiveness of the distributed cooperative control algorithm.
摘要
针对带有攻击角约束的多拦截弹协同拦截问题,基于制导与控制一体化(IGC)方法,提出了一种带有攻击角约束的多拦截弹分布式协同控制算法。首先,基于弹目相对运动关系和拦截弹俯仰通道动力学方程,建立带有攻击角约束的拦截弹"领弹"IGC模型,利用变增益扩张状态观测器(TVGESO)对模型中的未知干扰进行估计,在此基础上,基于干扰估计值和非奇异动态面滑模控制设计"领弹"控制算法;其次,采用基于"领弹-从弹"的分布式网络模式,设计多拦截弹协同控制策略,可以得到拦截弹在俯仰通道2个方向的速度分量,利用运动学转换关系转化为速度和弹道倾角参考指令;最后,基于TVGESO和动态面滑模控制设计"从弹"的控制算法。仿真结果验证所设计的带有攻击角约束的多拦截弹协同IGC算法具有较好的稳定性。
Key words: impact angle constraints / integrated guidance and control / extended state observer / dynamic surface sliding control / distributed cooperative control algorithm / cooperative control strategy
关键字 : 攻击角约束 / 制导控制一体化 / 扩张状态观测器 / 动态面滑模控制 / 分布式网络 / 协同控制策略
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
多拦截弹协同制导与控制打破了传统单枚拦截弹作战中没有合作的传统思想, 为适应未来战场的复杂环境应运而生。多拦截弹协同打击目标, 是将多枚拦截弹作为一个整体组成信息共享的网络, 在网络内的拦截弹可以进行数据交换, 通过数据交换实现共同打击的目的, 可以提高拦截弹的打击和突防能力[1-2]。
在传统拦截弹的制导与控制系统的设计方法中, 将拦截弹制导控制系统分为控制回路和制导回路, 分别对2个子系统进行设计, 不考虑2个回路之间的耦合关系。制导与控制一体化设计根据弹体与目标的相对运动信息和拦截弹的运动信息产生控制力, 驱动拦截弹打击目标, 既能保持拦截弹飞行姿态的稳定又能提高制导精度[3-4]。
在制导控制一体化研究方面, 近年来国内外专家学者进行了大量的研究。其中Ran等[5]利用自适应算法逼近系统的耦合, 设计了自适应控制律对未知参数进行估值, 最后控制器设计采用反演滑模控制方法。Shtessel等[6-7]研究了运用高阶滑模控制方法和反演控制算法设计了制导控制一体化控制律。Wu等[8]研究了将导弹的制导控制一体化模型利用非线性变换转化为可控型模型, 并设计具有攻角约束的制导控制一体化算法。董飞垚等[9]基于零视化视线角速率的原理, 设计有限时间控制律, 并利用超螺旋算法对系统的不确定进行补偿。Liang等[10-11]在反演控制方法的基础上, 加入了饱和影响因素并引入执行机构动态模型, 设计了飞行器纵向抗制导与控制一体化算法。
在协同制导与控制方面, 其中后德龙等[12]构造了“领弹-从弹”的拓扑网络, 并将目标作为领弹, 提出了一种位置同步算法实现协同制导。赵启伦等[13]设计了“领弹-从弹”拓扑结构的多导弹协同制导律, 并给出了协同制导律在固定拓扑和切换拓扑的条件。周慧波等[14]等针对系统中存在的扰动和不确定性, 提出了一种基于通讯拓扑的鲁棒自适应协同控制策略。王晓芳等[15]将导弹的六自由度模型简化, 得到导弹的四维精确制导控制一体化模型, 但实质还是分别设计快回路与慢回路算法。
在带约束攻击角的协同控制方面, 张春研等[16]研究了带有攻击角约束和攻击时间约束的协同偏执比例制导律。宋俊红等[17]采用滑模控制方法, 提出了一种带有攻击角约束协同制导律。以上综述可以看出, 目前专家对多拦截弹协同控制的研究基本可分为两类, 一类是研究协同控制律, 另一类是研究协同制导律, 对于多拦截弹协同制导与控制一体化的研究非常有限。拦截弹制导与控制一体化设计方法能够有效的降低设计周期, 提高拦截弹系统的稳定性。
因此, 本文在拦截弹制导与控制一体化方法的基础上, 基于分布式网络协同控制策略和动态面滑模控制理论, 提出了一种带有攻击角约束的多拦截弹协同制导与控制一体化算法, 使多拦截弹之间具有信息交换, 并且能够以期望的攻击角击中目标。最后并利用仿真验证设计算法的有效性。
1 攻击角约束的多拦截弹协同制导控制问题
1.1 问题描述
研究具有攻击角约束的多拦截弹协同制导与控制问题, 是为了寻找一种协同控制策略, 使得多发拦截弹能够以期望相同的攻击角度击中目标, 不仅能够提高多拦截弹的突防能力, 还能进一步提高多拦截弹的杀伤力和全方位的攻击能力。
考虑“领弹-从弹”模式的协同控制策略问题如图 1所示, 假设“领弹”配备高性能导引头可以探测目标的运动信息, “从弹”不配备导引头, 而是通过信息交换获取飞行信息, 渐进收敛到“领弹”的位置。
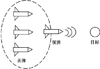 |
图1 协同控制策略 |
1.2 “领弹”制导与控制一体化模型
基于拦截弹俯仰通道, 拦截弹和目标之间的相对运动关系如图 2所示。
图中, M和T分别为拦截弹和攻击目标; am4ε和atε分别为拦截弹和目标运动加速度; Vm和Vt分别为拦截弹和目标的速度; θm和θt分别为拦截弹和目标的弹道倾角; qε为弹-目视线角; r表示拦截弹与目标之间的相对距离。建立拦截弹在纵向平面的相对运动模型为:
攻击角可表述为拦截过程中制导结束时刻拦截弹速度矢量与目标速度矢量之间的夹角。当拦截弹打击目标时, 攻击角即为拦截弹速度矢量角。定义制导结束时刻为tf, 拦截弹期望的攻击角为φd。攻击角约束问题是指在制导结束时刻, 保证拦截弹击中目标的同时以期望的攻击角击中目标, 即满足:
(4) 式表示拦截弹在击中目标时, 目标在视场范围内, 由(1)式和(2)式可得
对于具体攻击任务的拦截弹, 期望的攻击角φd为定值, 假设θt(tf)可知, 由(3)式可知拦截弹在制导结束时刻的弹道倾角θm(tf)也是定值, 由(4)式和(5)式可得到确定且唯一的期望终端视线角, 定义为qd, 则攻击角约束就转化为终端视线角问题[18], 且满足qε(tf)=qd。
拦截弹“领弹”在俯仰通道动力学模型采用如下表达方式:
式中,S为“领弹”参考面积, q为动压, 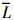 为“领弹”长度, m为“领弹”质量, α为攻角, ωz为俯仰角速度, dα和dωz分别为系统中各个环节的扰动和不确定干扰, Jz为导弹的转动惯量, Cyα, mzα, mzωz为气动力和力矩系数; Mz为俯仰通道控制力矩。
为“领弹”长度, m为“领弹”质量, α为攻角, ωz为俯仰角速度, dα和dωz分别为系统中各个环节的扰动和不确定干扰, Jz为导弹的转动惯量, Cyα, mzα, mzωz为气动力和力矩系数; Mz为俯仰通道控制力矩。
假设拦截弹在末制导阶段的视线角变化不大, 拦截弹的视线角方向与速度方向的夹角较小[10-11], 则可得am4ε≈am3ε。同时,拦截弹制导控制一体化系统的未知干扰dα和dωz连续可微, 且其导数有界。根据(1)式和(6)式, 定义x1=qε-qd, x2=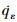 , x3=α, x4=ωz, 可得到具有攻击角约束的拦截弹“领弹”在俯仰通道的制导与控制一体化非线性模型为:
, x3=α, x4=ωz, 可得到具有攻击角约束的拦截弹“领弹”在俯仰通道的制导与控制一体化非线性模型为:
式中,atε为目标的横向加速度, 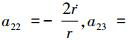
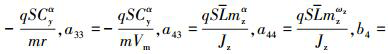
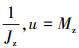 。
。
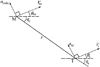 |
图2 拦截弹和目标之间的相对运动 |
2 拦截弹“领弹”控制器设计
2.1 变增益扩张状态观测器(TVGESO)设计
扩张状态观测器可以对系统模型中具有非线性的不确定项进行估值, 将估值反馈到控制系统中进行补偿。针对系统模型(7)中包含的未知不确定干扰atε, dα, dωz, 为消除上述未知干扰对拦截弹领弹控制系统的影响, 设计变增益扩张状态观测器(TVGESO)对进行未知干扰进行估值。
定义 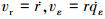 , 由(1)式可得:
, 由(1)式可得:
设计如下形式的TVGESO对目标的横向加速度atε进行估值, 可得:
式中,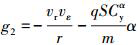 , v21和v22分别是vε和atε的估计值, e21和e22分别是估计误差, λ21和λ22分别为状态观测器待设计变增益系数。
, v21和v22分别是vε和atε的估计值, e21和e22分别是估计误差, λ21和λ22分别为状态观测器待设计变增益系数。
设计变增益系数为:λ21=2L(t), λ22=L2(t)。定义函数L(t)为
式中,γ为自适应系数, 且γ>0。由参照文献[19]可知, 选择合适的系数可保证变增益扩张状态观测器误差系统在有限时间是稳定的。
同理, 对(7)式中的攻角回路和俯仰角速度回路的干扰dα和dωz进设计估值, 可得:
式中,g3=a33x3+x4, g4=a43x3+a44x4+b4u, 未知干扰dα和dωz的估计值分别为v32和v42, 估计误差分别为e32和e42。
2.2 非奇异快速动态面滑模控制器设计
由于拦截弹制导控制一体化模型是非匹配不确定系统, 针对IGC模型(7)和TVGESO估计值(9)~(11)式, 采用动态面滑模控制作为拦截弹“领弹”的控制算法。
1) 根据动态面滑模控制设计方法, 考虑(7)式第2个子系统, 定义x2d为系统跟踪指令信号。
定义第1个动态误差面:
对s2求导, 可得误差动态方程为:
将(9)式中TVGESO估计值v22代入(13)式, 可得到第1个动态面的虚拟控制量
式中,k2>0。为了避免对虚拟控制量求导过程中引起的项数膨胀带来的复杂计算过程, 将x3*通过一阶低通滤波器, 可得滤波的虚拟控制量为:
式中, τ3为滤波器的时间常数, 则可得误差面滤波后的虚拟控制量的微分为:
2) 定义第2个动态误差面为:
对s3求导, 可得误差动态方程为
基于第1个动态面方法将(10)式中TVGESO估计值v32代入, 可得第2个动态面的虚拟控制量为
式中,k3>0。使x4*通过如下低通滤波器, 可得
式中,τ4为滤波器时间常数, 可得到误差面滤波后的虚拟控制量的微分为
3) 定义第3个动态误差面:
对s4求导, 可得误差动态方程为
为保证(22)式在有限时间内快速地收敛到平衡位置, 设计如下非奇异快速滑模趋近律
式中,p, q∈N+且为奇数, 1 < p/q < 2, ka>0, kb>0, 0 < ∂ < 1。
根据(23)~(24)式和(11)式中TVGESO估计值v42可得, 拦截弹“领弹”的非奇异快速动态面滑模控制律为
式中,k4>0, k5>0, 1 < p/q < 2, 0 < ∂ < 1。
2.3 稳定性分析
针对“领弹”制导与控制一体化系统(7), 如果趋近律采用(24)式, 利用TVGESO对系统(7)中外界干扰进行估值, 以及滤波算法(15)式和(20)式, 在设计的动态面滑模控制律(25)式的作用下, 系统(7)能在有限时间内渐进收敛。
证明 定义TVGESO系统的估计误差满足:
式中,N2, N3, N4为正常数。
定义滤波误差为:
对y3, y4求导可得滤波的动态误差:
由(12)~(22)式和(27)式可得
由(7)式、(12)~(22)式和(27)~(29)式可得:
式中,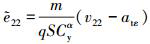 , 假设
, 假设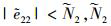 为正常数。
为正常数。
根据Young不等式, 由(29)式~(32)式, 可得:
可知系统模型中的变量与其微分都是有界, 则存在连续的函数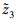 和
和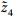 , 且满足
, 且满足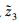 >0,
>0, 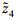 >0, 则使变量
>0, 则使变量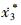 和
和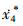 满足:
满足:
根据Young不等式, 由(27)式~(28)式和(36)式, 可得:
根据IGC非线性系统模型(7), 选取Lyapunov函数为:
对Lyapunov函数式(39)两边求导, 可得:
设计参数满足如下规则:
式中,κ为常数, 且满足κ>0, 则可得
式中
由(42)式可得:
因此, 通过设计参数k2, k3, k4, k5和参数τ3, τ4保证系统收敛。选择增加参数k2, k3, k4, k5和减小τ3与τ4, 可以保证κ足够大, 可使滤波误差和误差面达到足够小, 保证控制精度。证毕。
3 分布式网络协同策略
3.1 基于分布式网络的协同控制策略设计
由于只有“领弹”可以探测目标运动信息, 因此, 协同控制的目标是设计一个网络协同策略, 实现“从弹”位置渐进收敛于“领弹”的位置。构建一发“领弹”与n发“从弹”组成的“领弹-从弹”的拓扑结构, 该拓扑结构可以用无向图来描述。假设每一发拦截弹作为一个通讯节点, 则拦截弹之间的信息交换可用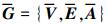 表示, 其中各拦截弹节点组成的集合表示为
表示, 其中各拦截弹节点组成的集合表示为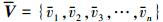 , 各个拦截弹节点之间连线表示为
, 各个拦截弹节点之间连线表示为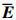 , 无向图的邻接矩阵表示为
, 无向图的邻接矩阵表示为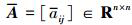 , 如果拦截弹节点i和节点j可以进行交换信息, 则满足
, 如果拦截弹节点i和节点j可以进行交换信息, 则满足 , 否则
, 否则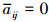 。
。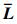 表示为无向图
表示为无向图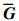 的Laplace矩阵, 其中元素满足:
的Laplace矩阵, 其中元素满足:
定义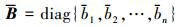 表示各个“从弹”是否能获取“领弹”的状态信息,
表示各个“从弹”是否能获取“领弹”的状态信息,  , i∈{1, 2, 3, …, n}表示各个“从弹”能够获得“领弹”的状态信息,
, i∈{1, 2, 3, …, n}表示各个“从弹”能够获得“领弹”的状态信息,  , i∈{1, 2, 3, …, n}表示各个“从弹”不能获得“领弹”的状态信息。
, i∈{1, 2, 3, …, n}表示各个“从弹”不能获得“领弹”的状态信息。
基于“领弹-从弹”的通讯拓扑结构, 设计多拦截弹的协同控制策略为:
式中,x0表示领弹的位置, xi, i∈{1, 2, 3, …, n}表示各个拦截弹的位置, 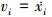 表示各个拦截弹的速度, ki1为常数, 且满足ki1>0。如果协同控制策略可以实现所有拦截弹“从弹”状态收敛于“领弹”状态, 则称协同控制策略达成。
表示各个拦截弹的速度, ki1为常数, 且满足ki1>0。如果协同控制策略可以实现所有拦截弹“从弹”状态收敛于“领弹”状态, 则称协同控制策略达成。
证明:
引理1 Laplace矩阵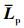 有以下性质:
有以下性质:
1) 若 是连通的,
是连通的, 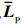 的特征值
的特征值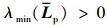 , 称为网络连通图的代数连通度,
, 称为网络连通图的代数连通度,  越大, 则表示网络越连通。
越大, 则表示网络越连通。
2) 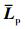 的一个特征值为0, 且1是其对应的特征向量, 其中1表示为n×1列向量。
的一个特征值为0, 且1是其对应的特征向量, 其中1表示为n×1列向量。
定义误差变量ei=xi-x0, 可得:
定义Lyapunov函数:
式中,e=[e1, e2, …, en]T.定义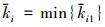 , 对(47)式左右两边求导, 可得
, 对(47)式左右两边求导, 可得
令V(e)≠0, 上式可得:
由(48)~(49)式, 可得
因此, 由引理1可知, V(t)在有限时间内是收敛的, 即拦截弹能收敛到领弹的状态, 实现多拦截弹协同制导与控制。证毕。
3.2 分布式网络协同控制策略实现
分布式多拦截弹协同控制策略的实质就是实现拦截弹“从弹”位置与拦截弹“领弹”位置的同步。因此, 为实现分布式网络同步策略, 网络中每发“从弹”需要对同步策略(45)给出的速度指令进行跟踪。
网络中参与协同拦截的拦截弹的运动关系为:
式中,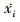 和
和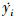 分别表示第i发拦截弹在惯性坐标系下的速度分量。
分别表示第i发拦截弹在惯性坐标系下的速度分量。
根据(45)式分布式网络同步策略, 可以得到“从弹”的速度参考指令为:
根据(51)式和(52)式, 可得
式中,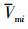 为拦截弹“从弹”的速度参考指令,
为拦截弹“从弹”的速度参考指令, 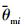 为拦截弹“从弹”的弹道倾角参考指令。
为拦截弹“从弹”的弹道倾角参考指令。
4 拦截弹“从弹”控制器设计
根据(53)式可以看出, 协同控制策略给出的指令可以转化为速度和弹道倾角指令, 为实现协同网络中拦截弹“从弹”对指令信号跟踪, “从弹”控制器采用动态面滑模控制算法。假设拦截弹“从弹”的速度是可控的, 设计“从弹”飞行速度, 忽略空气阻力和重力的影响, 拦截弹“从弹”的飞行速度可表示为
式中, Pi为发动机推力。
为保证系统能快速收敛到平衡位置, 采用如下滑模趋近律
式中,ka>0, kb>0, 0 < λ < 1。
基于滑模控制理论和(55)式, 设计拦截弹“从弹”推力为
式中,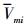 为速度参考指令, kv1>0, kv2>0, 0 < λv < 1。
为速度参考指令, kv1>0, kv2>0, 0 < λv < 1。
令xi1=θmi, xi2=αi, xi3=ωi, 则第i发“从弹”在俯仰通道的动力学方程可表示为:
式中,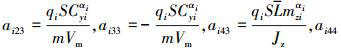
 。
。
根据(9)式~(11)式, 设计TVGESO对(57)式中的干扰进行估值, 则可得di1, di2和di3的估值分别为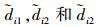 。
。
根据动态面滑模控制理论, 设计“从弹”控制算法。
1) 定义第1个动态误差面:
式中,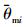 为弹道倾角参考指令。对si1求导, 可得
为弹道倾角参考指令。对si1求导, 可得
可得到第1个动态面的虚拟控制量
式中,ki1>0。为了避免对虚拟控制量求导过程中引起的项数膨胀带来的复杂计算过程, 将xi2*通过一阶低通滤波器, 可得滤波后的虚拟控制量及其微分为:
式中,τi2为滤波器时间常数, 且满足τi2>0。
2) 定义第2个动态误差面
对si2求导, 可得
同理第一个动态面设计方法, 可得第2个动态面的虚拟控制量:
式中, ki2>0, 将xi3*通过如下低通滤波器, 可得:
式中,τi3为滤波器时间常数, 且满足τi3>0。
3) 定义第3个动态误差面
对si3求导, 可得
根据(55)式, 设计拦截弹“从弹”动态面滑模控制律为:
式中,ki31>0, ki32>0, 0 < λi3 < 1。
根据(26)式~(43)式, 可以证明“从弹”控制算法的稳定性。
5 仿真验证
为验证设计的具有攻击角约束的多拦截弹协同制导与控制一体化算法的有效性, 假设拦截弹“领弹”可与另外3发“从弹”进行通信, “从弹”之间采用相邻通信的方式, “领弹”和“从弹”是在理想的通信环境中进行, 通讯拓扑结构如图 3所示。假设“从弹”运动轨迹收敛到“领弹”运动轨迹后, 将按照既定的编队方式进行飞行, 且“领弹”和“从弹”在空间位置上相互独立, 相互不会干扰。拦截弹的期望视线角qd=-30°, 拦截弹“领弹”和“从弹”的初始速度为460 m/s, “领弹”的速度保持不变, 目标的初始速度为200 m/s, “领弹”、“从弹”和目标的初始位置如表 1所示。
针对图 3的通讯拓扑结构, 假设系统存在的干扰为dα=dωz=di1=di2=di3=0.02sin(t), 按照如下2种拦截情形对本文设计的攻击角约束的多拦截弹协同制导控制一体化算法进行仿真研究。
情形1 目标匀速运动:atε=0 m/s2
情形2 目标做直线加速运动:atε=10 m/s2
图 4表示在目标做匀速运动的情形下, 拦截弹“领弹”、“从弹”和目标的运动轨迹, 从图中可以看出在协同控制策略的作用下, 拦截弹“从弹”的运动轨迹逐渐同“领弹”运动轨迹趋于一致, 最终实现了“领弹”和“从弹”协同拦截的目的, 运动轨迹曲线较平滑, 拦截时间较短, 且收敛速度较快, 具有较好的稳定性。图 5表示“领弹”和“从弹”的速度变化曲线, 从图中可以看出“从弹”的速度逐渐收敛到“领弹”的速度。图 6表示“领弹”和“从弹”的视线角变化曲线, 从图中可以看出“领弹”和“从弹”都收敛到相应的视线角期望值, 收敛过程较平滑, 对外部干扰具有较强的鲁棒性。图 7表示“领弹”和“从弹”的俯仰角速度曲线。目标运动情形2的仿真图, 如图 8至11所示。
图 8表示在目标做加速运动的情形下, 拦截弹“领弹”、“从弹”和目标的运动轨迹, 从图中可以看出“从弹”同样实现了跟随“领弹”对目标的协同拦截, 运动轨迹较平滑, 稳定性较好。图 10表示“领弹”和“从弹”的视线角变化曲线, 从图中可以看出在对加速运动目标拦截时, “领弹”和“从弹”都能在击中目标前收敛到相应的视线角期望值, 收敛过程较平滑, 对外部干扰具有较强的鲁棒性。
通过对2种情形下拦截目标的仿真结果可以看出, 设计的具有攻击角约束的多拦截弹协同制导控制一体化算法都可以较稳定的完成协同控制策略的指令跟踪并且以期望的视线角击中目标, 最终实现了多拦截弹协同拦截目标的任务。
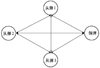 |
图3 拦截弹领弹与从弹通讯拓扑结构 |
拦截弹领弹、从弹和攻击目标的初始条件
 |
图4 情形1下拦截弹“领弹”、“从弹”和目标的运动轨迹 |
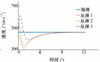 |
图5 情形1下拦截弹“领弹”和“从弹”速度曲线 |
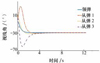 |
图6 情形1下拦截弹“领弹”和“从弹”视线角曲线 |
 |
图7 情形1下拦截弹“领弹”和“从弹”俯仰角速度曲线 |
 |
图8 情形2下拦截弹“领弹”、“从弹”和目标的运动轨迹 |
 |
图9 情形2下拦截弹“领弹”和“从弹”速度曲线 |
 |
图10 情形2下拦截弹“领弹”和“从弹”视线角曲线 |
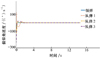 |
图11 情形2下拦截弹“领弹”和“从弹”俯仰角速度曲线 |
6 结论
针对具有攻击角约束的多拦截弹协同拦截问题, 结合制导与控制一体化方法, 并引入分布式协同控制策略, 设计了一种具有攻击角约束的多拦截弹协同制导控制一体化算法。分别采用了动态面滑模控制律和变增益扩张状态观测器设计了拦截弹“领弹”和“从弹”控制算法, 通过分布式协同控制策略保证“领弹”和“从弹”同时拦截目标。通过仿真验证了该算法具备较理想弹道特性, 在目标匀速运动和加速运动的条件下, 均能以期望的视线角实现对目标的协同拦截, 为多拦截弹协同拦截目标提供一种设计方法, 具有一定工程价值。
References
- Zhao S Y, Zhou R, Wei C, et al. Design of Time-Constrained Guidance Laws via Virtual Leader Approach[J]. Chinese Journal of Aeronautics, 2010, 23(1): 103–108 [Article] [CrossRef] [Google Scholar]
- Xiao Zengbo, Lei Humin, Teng Jiangchuan, et al. The Present Status and Prospect of Multi-Missile Cooperative Guidance Law Aero Weaponry, 20116): 18–22 (in Chinese) [Article] [Google Scholar]
- Xue Wenchao, Huang Chaodong, Huang Yi. Design Methods for the Integrated Guidance and Control System Control Theory & Applications, 2013, 30(12): 1511–1520 (in Chinese) [Article] [Google Scholar]
- Hou M Z, Liang X L, Duan G Z. Adaptive Block Dynamic Surface Control for Integrated Missile Guidance and Autopilot[J]. Chinese Journal of Aeronautics, 2013, 26(3): 741–750 [Article] [CrossRef] [Google Scholar]
- Ran M P, Wang Q, Hou D L, et al. Back Stepping Design of Missile Guidance and Control Based on Adaptive Fuzzy Sliding Mode Control[J]. Chinese Journal of Aeronautics, 2014, 27(3): 634–642 [Article] [CrossRef] [Google Scholar]
- Shtessel Y B, Shkolnikov I A, Levant A. Guidance and Control of Missile Interceptor Using Second-Order Sliding Modes[J]. IEEE Trans on Aerospace and Electronic Systems, 2009, 45(1): 110–124 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Shtessel Y B, Tournes C H. Integrated Higher Order Sliding Mode Guidance and Autopilot for Dual-Control Missiles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 79–94 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Wu P, Yang M. Integrated Guidance and Control Design for Missile with Terminal Impact Angle Constraint Based on Sliding Mode Control[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 623–628 [Article] [CrossRef] [Google Scholar]
- Dong Feiyao, Lei Humin, Zhou Chijun, et al. Research of Intergrated Robust High Order Sliding Mode Guidance and Control for Missiles Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2212–2218 (in Chinese) [Article] [Google Scholar]
- Liang X L, Hou M Z, Duan G R. Integrated Guidance and Control for Missile in the Presence of Input Saturation and Angular Constrains[C]//Proceedings of the 32nd Chinese Control Conference, Xi'an, China, 2013: 1070–1075 [Google Scholar]
- Liang X L, Hou M Z, Duan G R. Adaptive Dynamic Surface Control for Integrated Missile Guidance and Autopilot in the Presence of Input Saturation[J]. Journal of Aerospace Engineering, 2015, 28(5): 401–412 [Article] [Google Scholar]
- Hou Delong, Chen Bin, Wang Qing, et al. Collision Avoidance Multi-Missiles Distributed Cooperative Guidance and Control Control Theory and Applications, 2014, 31(9): 1133–1142 (in Chinese) [Article] [Google Scholar]
- Zhao Qilun, Chen Jian, Dong Xiwang, et al. Cooperative Guidance Law for Heterogeneous Missiles Intercepting Hypersonic Weapon Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 936–948 (in Chinese) [Article] [Google Scholar]
- Zhou Huibo, Song Shenmin, Zheng Zhong. Distributed Robust Adaptive Control for Missile Cooperative Engagement within Formation Journal of Chinese Inertial Technology, 2015, 23(4): 516–527 (in Chinese) [Article] [Google Scholar]
- Wang Xiaofang, Zheng Yiyu, Lin Hai. 4D Integrated Guidance and Control Law for Missiles Cooperative Engagement Systems Engineering and Electronics, 2015, 37(4): 874–881 (in Chinese) [Article] [Google Scholar]
- Zhang Chunyan, Song Jianmei, Hou Bo, et al. Cooperative Guidance Law with Impact Angle and Impact Time Constraints for Networked Missiles Acta Armamentarii, 2016, 37(3): 431–438 (in Chinese) [Article] [Google Scholar]
- Song Junhong, Song Shenmin, Xu Shengli. Cooperative Guidance Law for Multiple Missiles with Impact Angle Constraints Journal of Chinese Inertial Technology, 2016, 24(4): 554–560 (in Chinese) [Article] [Google Scholar]
- Sun Sheng, Zhang Huaming, Zhou Di. Sliding Mode Guidance Law with Autopilot Lag for Terminal Angle Constrained Trajectories Journal of Astronautics, 2013, 34(1): 69–78 (in Chinese) [Article] [Google Scholar]
- Lu Xiaodong, Zhao Hui, Zhao Bin, et al. Disturbance Compensation-Based Integrated Guidance and Control Design for Near Space Interceptor Control and Decision, 2017, 32(10): 1782–1788 (in Chinese) [Article] [Google Scholar]
All Tables
All Figures
 |
图1 协同控制策略 |
| In the text | |
 |
图2 拦截弹和目标之间的相对运动 |
| In the text | |
 |
图3 拦截弹领弹与从弹通讯拓扑结构 |
| In the text | |
 |
图4 情形1下拦截弹“领弹”、“从弹”和目标的运动轨迹 |
| In the text | |
 |
图5 情形1下拦截弹“领弹”和“从弹”速度曲线 |
| In the text | |
 |
图6 情形1下拦截弹“领弹”和“从弹”视线角曲线 |
| In the text | |
 |
图7 情形1下拦截弹“领弹”和“从弹”俯仰角速度曲线 |
| In the text | |
 |
图8 情形2下拦截弹“领弹”、“从弹”和目标的运动轨迹 |
| In the text | |
 |
图9 情形2下拦截弹“领弹”和“从弹”速度曲线 |
| In the text | |
 |
图10 情形2下拦截弹“领弹”和“从弹”视线角曲线 |
| In the text | |
 |
图11 情形2下拦截弹“领弹”和“从弹”俯仰角速度曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


