| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 824 - 829 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740824 | |
| Published online | 23 September 2019 | |
Permanent Magnet Synchronous Motor Speed Control System Based on Adaptive Inverse Control Method
基于自适应逆控制的永磁同步电机调速系统
School of Automation, Northwestern Polytechnical University, Xi’an 710072, China
Received:
15
September
2018
The classical feedback control method for the permanent-magnet synchronous motor cannot fulfill the dynamic requirement and anti-interference requirement at the same time. In this paper, an adaptive inverse control method with disturbance elimination is proposed based on the vector control including speed and current loops. It avoids the system instability and the anti-disturbance performance of the system can be enhanced as well. Firstly, the speed loop adopts the adaptive inverse controller possessing a feed forward control structure, and a normalized least-mean square filtering algorithm accelerates the speed error convergence. The inverse model of the approximately linearized system is obtained by modifying the weighting factor online. Secondly, in order to suppress and eliminate the influence of motor parameter perturbation and external disturbance on the control system, an extended state observer is designed to observe and compensate the disturbance of the system. Thus, the dynamic performance and anti-disturbance performance of the system can be improved simultaneously. Finally, the effectiveness of the proposed method is verified by experiment and simulation.
摘要
针对永磁同步电机的反馈控制方法要兼顾系统动态性和抗扰性需求,在双闭环的矢量控制中采用具有扰动消除环节的自适应逆控制方法,能够避免系统的不稳定现象,提高系统的抗扰性能。首先,转速环采用基于前馈控制的自适应逆控制器,通过归一化的最小均方滤波算法使得转速误差能够快速收敛,并通过在线修正控制器权值,得到近似线性化的被控对象的逆模型。其次,为了抑制和消除电机参数摄动和外部扰动对系统的影响,采用扩张状态观测器对系统的扰动进行观测并补偿,同时提高系统动态性能和抗扰性能。最后,通过实验和仿真验证了所提方法的有效性。
Key words: permanent magnet synchronous motor / adaptive inverse controller / normalization of least mean square filtering / extended state observer / vector control / anti-disturbance / stability
关键字 : 永磁同步电机 / 自适应逆控制器 / 归一化最小均方滤波 / 扩张状态观测器
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
永磁同步电机具有高阶、多变量、非线性、强耦合、参数摄动等特点[1], 使得采用传统控制方式下的系统难以完全解耦。另外, 经典的反馈控制系统在保持稳定的前提下很难使对象扰动消除和动态控制效果同时达到最佳, 限制了控制性能的进一步提升。
自适应逆控制器[2](adaptive inverse controller, AIC)通过自适应滤波算法获得近似被控对象传递函数的逆模型作为控制器, 将其串入系统实现控制。该方法是一种开环控制, 能够避免系统因反馈而导致的不稳定现象, 可以将系统动态特性和抑制扰动进行独立控制。AIC与内模控制类似, 都是通过在系统的前向通道串入对象的逆模型, 实现输出跟随输入的目的, 但内模控制需要考虑控制器的可实现性, 通过设计不同阶数的控制器实现对给定信号的无差跟踪。当控制器阶数过低时, 不能有效跟踪给定信号; 当控制器阶数过高时, 不利于其数字化实现[3]。相反, AIC通过滤波算法近似被控对象的逆模型, 不需要被控对象严格意义上存在逆系统。
文献[4]在飞行控制系统中采用具有对象噪声和扰动消除的模型参考自适应逆控制, 自适应算法采用基于BP神经网络的权值寻优方法, 避免局部最优并提高了收敛速度, 使得对象动态响应控制和扰动消除控制独立考虑。该方法虽然提高了系统的动态性能, 但是系统的结构复杂, 运算量较大。文献[5]将自适应逆控制应用在需要具有很高的动态特性的电动舵机控制系统中, 采用了最小均方(least mean square, LMS)滤波器进行在线电动舵机逆系统建模, 并将逆模型作为前向通道的控制器, 建立了补偿模型, 提高了系统跟踪性能, 改善了位置跟踪的相位滞后问题。文献[6]针对多变量、非线性、强耦合的无轴承异步电机的悬浮系统, 利用非线性自适应滤波器对悬浮系统进行自适应建模与逆系统建模, 复制逆模型, 将其串联在系统之前作为自适应逆控制器, 同时采用变步长LMS算法在线调节权值系数, 解决了系统的动态解耦问题。文献[7]针对永磁同步电机控制系统, 采用改进的径向基函数神经网络与FIR滤波器并联作为非线性自适应滤波器, 用于系统的建模辨识、扰动消除、自适应逆控制器设计; 同时采用改进的变步长LMS算法对非线性滤波器的参数进行在线优化, 提高了非线性滤波器的收敛速度和精度, 但系统较为复杂。文献[8]将自适应逆控制方法引入矢量控制中的速度控制, 采用基于LMS自适应滤波算法在线调整权函数, 实现了速度控制, 但自适应逆控制中的扰动消除环节采用了离线的对象建模和对象逆建模, 没有考虑实际电机运行过程中电机参数变化导致的模型误差。文献[9]将自适应逆控制应用于非线性的航空发动机控制系统中, 采用横向滤波器对系统实现近似线性化的建模和逆建模, 同时为了解决系统中的稳态误差, 提出了带积分环节的自适应逆控制结构, 提高了系统的稳态精度, 但是没有考虑系统的外部扰动。
本文为了提高系统的动态性和抗扰性, 设计了一种基于自适应逆控制的永磁同步电机调速系统。转速环采用自适应逆控制器, 通过基于归一化的LMS自适应滤波算法, 在线调节控制器权值来估计被控对象的逆模型, 保证转速跟踪快速收敛。同时, 通过构建扩张状态观测器(extend state observer, ESO)进行在线观测扰动误差, 并进行实时补偿, 相比其他的自适应逆扰动消除方法, 该方法可以减小控制系统的复杂度, 同时降低在线运算量。
1 永磁同步电机的数学模型
永磁同步电机是一个高阶、非线性、强耦合的复杂系统, 因此为了简化分析过程, 常作如下假设[10]:忽略空间谐波, 并设定子三相绕组对称, 在空间中互差120°电角度, 所产生的磁动势沿气隙按正弦规律分布; 忽略磁路饱和, 各绕组电感值恒定; 忽略铁芯损耗; 绕组电阻值恒定。在dq两相旋转坐标系下, 电磁转矩方程可表示为(1)式
式中, Te为电磁转矩, ψf为永磁体磁链, iq和id分别为q轴和d轴的定子电流, np为极对数, Ld和Lq分别为定子d轴和q轴电感。对于隐极式电机有Ld=Lq, 则电磁转矩方程可简化为
忽略外部扰动, 电机的运动方程可表示为
式中, TL为负载转矩, J为转动惯量, B为黏滞摩擦因数, ωr为机械角速度。假设反馈电流完全跟随给定电流, 并且忽略负载转矩, 则(3)式可化简为
式中, 系数b=1.5np2ψf/J。以q轴电流给定为输入, 电机转速为输出的系统传递函数可表示为
因此, 该系统的逆模型存在并且稳定, 用传递函数形式可以表示为
式中, 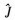 为转动惯量的估计值;
为转动惯量的估计值; 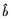 为粘滞摩擦因数的估计值;
为粘滞摩擦因数的估计值;  为系数b的估计值。
为系数b的估计值。
2 自适应逆控制系统
永磁同步电机自适应逆控制调速系统整体框图见图 1, 主要包含转速控制器、电流控制器、扩张状态观测器、SVPWM调制模块、两电平逆变器、电机本体、转子位置检测部分等。转速环的控制采用基于归一化最小均方滤波算法修正权值的自适应逆控制器, 实现对转速环的精确跟踪; 同时, 结合二阶的非线性扩张状态观测器, 对系统的扰动进行抑制, 即AIC+ESO的控制方式。电流环的控制采用双PI控制器, 实现对电流的近似解耦控制。
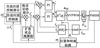 |
1 基于自适应逆控制的永磁同步电机调速系统原理框图 |
2.1 基于归一化LMS的自适应滤波算法
自适应逆控制系统中, 控制器的本质结构为可调权值的自适应滤波器, 通过自适应滤波算法在线调节控制器的权值, 得到近似线性化的电机逆模型并串入被控电机系统的前级, 近而实现输出转速跟随给定的控制效果。图 2为自适应滤波算法示意图。
对于自适应滤波器的权值更新方法, 传统LMS算法采用误差向量e(n)的平方代替均方误差J(n)进行估计, 即瞬时梯度估计
式中, e(n)=d(n)-wT(n)u(n), d(n)为控制器理想的输出给定电流向量, n为滤波器的长度。递推表达式有
μ为决定收敛快慢和稳定性的系数。LMS算法沿误差超曲面梯度最大的方向搜索, 逼近误差超曲面梯度为零的平衡点, 但该点可能不稳定或是局部极小点, 使得算法陷入局部最小值。同时, 算法迭代是基于误差梯度为零的权矢量的精确解, 增加了算法的时间。
本文采用归一化LMS算法, 将权向量迭代式中的修正项用u(n)的平方欧几里得范数归一化, 使得梯度噪声不会因输入向量的变化而放大。同时, 遵循最小化干扰原理, 即自适应滤波器权向量迭代过程以最小方式改变, 且受到更新优化准则的约束, 即δw(n+1)=w(n+1)-w(n)的欧几里得范数最小, 并满足d(n)=wT(n+1)u(n)。算法的性能函数可表示为
式中, λ为拉格朗日算子。为得到J(n)的最小权向量, 有
则可得最优更新权向量为
带入约束条件有
整理可得
将λ带入最优更新权向量得
为了更好地控制修正项的变化, 引入常量μ; 同时, 为了防止‖u(n)‖2过小影响控制, 引入常量γ; 为了提高动态性能, 在不改变收敛方向的情况下, 引入遗忘因子η, 弱化上一时刻的权值对当期状态产生的影响程度, 则权值迭代公式可表示为
由于权值迭代公式的修正项为变参数项, 因此归一化LMS算法是一种变步长算法, 可以加快响应时间、缩短收敛过程。
本文将归一化LMS算法应用到转速环的自适应逆控制器中, 其原理框图见图 3。
将永磁同步电机控制系统的输出转速与给定转速作差得到转速误差, 并作为归一化的LMS自适应滤波器的输入, 通过在线修正控制器的权值, 使控制器能够近似为被控对象的逆模型, 进而使得输出转速能够跟随输入的给定转速, 实现电机系统的转速控制。其中, 参考模型为纯延时环节, 延迟的周期为实际系统中转速环的调节周期。
其中, 自适应滤波算法的输入为给定转速, 控制器的输出为q轴电流给定信号, 误差为给定转速与输出转速的差值。因此, 在k时刻的输入向量可表示为ωr(n)={ωr*(k), ωr*(k-1), …, ωr*(k-n)}; 权值向量可表示为w(n)={w(k), w(k-1), …, w(k-n)}。为了提高系统的动态性, 用当期k时刻的转速误差作为将自适应滤波算法的误差信号, 即e=ωr*(k)-ωr(k)。此时, 归一化LMS的权值迭代公式可表示为
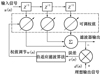 |
图2 自适应滤波算法示意图 |
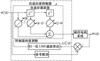 |
3 自适应逆控制原理框图 |
2.2 基于扩张状态观测器的扰动消除方法
(3) 式中的永磁同步电机运动方程是在不考虑外部扰动的情况下得到的, 当考虑实际外部扰动对系统产生的影响, 可得如下方程
式中, TL为负载转矩, J为转动惯量, B为粘滞摩擦因数, d为外部扰动, ωr为机械角速度, 化简得
式中, 系数b=1.5np2ψf/J, d1=-b(iq*-iq)-np(TL+d)/J。
为了消除电机参数摄动、外部负载扰动等对系统造成的影响, 本文通过建立扩张状态观测器对系统中存在的扰动量进行观测, 并对其产生的影响进行反馈补偿。结合电机的运动方程式(4)可得如下的扩张状态观测器的数学表达式
式中, 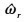 为估计的机械角速度,
为估计的机械角速度, 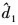 为估计的系统总扰动, β1和β2为系数。ESO的原理框图如图 4所示, 实现对扰动量的估计和对电流的补偿。
为估计的系统总扰动, β1和β2为系数。ESO的原理框图如图 4所示, 实现对扰动量的估计和对电流的补偿。
 |
图4 ESO的扰动观测和补偿原理框图 |
3 实验验证
本节通过实验验证所提控制算法有效性。控制参数:母线电压Udc=100 V, 开关频率fs=10 kHz, 电流环运算周期Tc=10-4 s, 转速环运算周期Ts=5×10-4 s。实验电机参数为:额定功率PN=18 kW, 额定转速ωN=1 200 r/min, 极对数np=4, 定子电阻Rs=0.106 Ω, 电感值Ls=Ld=Lq=2.4 mH, 磁链系数Ψf=0.199 Wb, 转动惯量Jn=0.017 6 kg·m2, 黏滞摩擦因数B=0。归一化最小均方算法的参数为:μ=7.2, γ=0.2, η=0.1。ESO的参数:β1=2 000, β2=12 000。
图 5为不同给定转速下的速度响应曲线, 在3 s时刻给定转速5 rad/s, 其他时刻分别给定转速50, 30, 10 rad/s。从图中可以看到, 加入ESO的自适应逆控制方法在调速过程中具有更短的上升时间。
图 6为给定转速(10 rad/s)在稳态时突加、突卸负载情况下, 转速和相电流响应曲线。从图中可以看出, 采用加入ESO的自适应逆控制方法在突加负载后, 转速能够迅速跟踪给定值; 但是未加入ESO的自适应逆控制方法在突加负载后, 转速掉落0.14 rad/s。因此, 采用ESO的自适应逆控制方法具有更好的鲁棒性。
图 7为电机三相串入电感, 使得等效电感值增加2.25倍后, 给定转速10 rad/s的转速响应波形, 可以看出空载稳态过程中, 未加入ESO的自适应逆控制方法下的输出转速存在0.2 rad/s的静差, 加入ESO的自适应逆控制方法不存在稳态误差。当突加负载后, 2种方法下转速都存在一定程度振荡, 但加入ESO的自适应逆控制方法可以使得转速仍然保持在10 rad/s的给定转速上, 但未加入ESO的自适应逆控制方法存在0.5 rad/s的转速静差。因此, 加入ESO的自适应逆控制方法在参数摄动的情况下, 仍然具有较好的鲁棒性和动态性能。
 |
5 不同转速范围的速度响应 |
 |
图6 突加、突卸负载 |
 |
7 电感参数变化的速度响应 |
4 结论
为了提高永磁同步电机转速控制系统的动态性和抗扰性, 本文采用了具有ESO扰动消除和归一化LMS自适应滤波算法结合的自适应逆控制方法, 应用于永磁同步电机的转速环控制器。通过基于归一化的LMS自适应滤波算法, 在线估计被控对象的逆模型, 并调节转速环控制器的权值, 使得控制器能够对给定转速实现快速跟踪, 保证系统具有快速的收敛速度和稳态精度。另外, 针对自适应逆控制的扰动消除, 本文通过构建扩张状态观测器来观测系统总扰动, 并进行反馈补偿, 有效地提高了系统的鲁棒性。仿真和实验结果证明了所提方法的有效性。
References
- Ruan Yi, Chen Boshi. Control Systems of Electric Drives-Motion Control Systems. Beijing, China Machine Press, 2010 (In chinese) [Google Scholar]
- Gebregergis A, Chowdhury M, Islam M, et al. Modeling of Permanent Magnet Synchronous Machine including Torque Ripple Effects[C]//Energy Conversion Congress and Exposition Denver, 2013: 2108–2114 [Article] [Google Scholar]
- Liu C, Luo G, Xue Z, et al. A PMSM Speed Servo System Based on Internal Model Control with Extended State Observer[C]//Conference of the IEEE Industrial Electronics Society, 2017: 1729–1734 [Google Scholar]
- Lin Jian. Model Reference Adaptive Dynamic Inversion Flight Control Based on Neural Networks[D]. Nanjing, Nanjing University of Aeronautics and Astronautics, 2013 (In chinese) [Google Scholar]
- Wang Houhao, Tang Dejia, Chen Hui, et al. Control of Electric Actuator for Spinning Missile Based on Adaptive Inverse[C]//Proceedings of the 36th Chinese Control Conference. Dalian: China Automation Society Control Theory Specialized Committee, Dalian, 2017: 3458–3462(in Chinese) [Google Scholar]
- Sun Yuxin, Yang Yuwei. Adaptive Inverse Decoupling Control for Bearingless Induction Motors Based on Nonlinear Filter[J]. Trans of the Chinese Society of Agricultural Engineering, 2016, 32(14): 76–83 [Article] (In chinese) [Google Scholar]
- Gong Yulin. Design and Implementation of Adaptive Inverse Control for Permanent Magnet Synchronous Motor[J]. Journal of Changchun University of Science and Technology, 2015(4): 61–64 [Article] (In chinese) [Google Scholar]
- Geng Jie, Chen Zhen, Liu Xiangdong, et al. Adaptive Inverse Control of Permanent Magnet Synchronous Motor[J]. Trans of China Electrotechnical Society, 2011, 26(6): 51–55, 61 [Article] (In chinese) [Google Scholar]
- Hu Wenfei, Huang Jinquan. Study of Aeroengine Adaptive Inverse Control[J]. Journal of Aerospace Power, 2005(2): 293–297 [Article] (In chinese) [Google Scholar]
- Sun Xudong, Wang Shanming. Electric Machinery[M]. Beijing, Tsinghua University Press, 2006 (In chinese) [Google Scholar]
All Figures
 |
1 基于自适应逆控制的永磁同步电机调速系统原理框图 |
| In the text | |
 |
图2 自适应滤波算法示意图 |
| In the text | |
 |
3 自适应逆控制原理框图 |
| In the text | |
 |
图4 ESO的扰动观测和补偿原理框图 |
| In the text | |
 |
5 不同转速范围的速度响应 |
| In the text | |
 |
图6 突加、突卸负载 |
| In the text | |
 |
7 电感参数变化的速度响应 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


