| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 816 - 823 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740816 | |
| Published online | 23 September 2019 | |
A Recognition Algorithm for Modulation Schemes by Convolution Neural Network and Spectrum Texture
基于卷积神经网络与时频图纹理信息的信号调制方式分类方法
Institute of Information and Navigation, Air Force Engineering University, Xi'an 710077, China
Received:
23
July
2018
The recognition of modulation schemes for communication signals is an important part of communication surveillance and spectrum monitoring. An algorithm based on deep learning and spectrum texture is proposed to recognize modulation schemes. Based on imperceptible differences among various spectrums of modulation schemes, the algorithm uses Convolution Neural Network to capture the features of image texture and thus classify the features with a SOFTMAX classifier. The experiment shows the algorithm performs better than traditional algorithm based on feature parameters, while the features captured can better reveal the signal detail and reduces effort on feature parameter design.
摘要
通信信号的调制方式识别是通信侦察、频谱监测的重要工作内容之一,提出一种利用深度学习提取信号时频图纹理信息的分类方法。该方法利用不同调制方式在时频图细节上的微弱差别,并使用卷积神经网络提取图像纹理特征,最终输入SOFTMAX分类器进行分类。结果表明,该方法在大样本条件下,可取得良好的分类效果。与传统基于特征参数的支持向量机分类方法或前馈神经网络方法相比,其提取特征更优、分类效果更好,同时减少了人工设计特征参数的工作量和不确定性。
Key words: modulation classification / spectrum texture / deep learning / convolution neural network / algorithm
关键字 : 调制识别 / 时频图纹理信息 / 深度学习 / 卷积神经网络
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
由于在通信侦察、频谱监测等领域中的重要作用,通信信号调制方式的自动识别一直是通信信号处理的主要研究内容之一。特别是复杂电磁环境下的调制方式自动识别,由于受到通信信号种类繁多、信噪比低、信道衰落及信号自适应变化等影响,其识别效果还无法满足实用要求。目前除了对卫星通信的信号监测应用以外,国内外尚无完全满足应用需要的无线电信号自动识别和分类系统。因此,在现有研究成果的基础上,研究探索应用新技术提升复杂电磁环境下通信信号自动识别和分类的性能具有重要意义。
当前,信号分类问题广泛采用基于特征的方法[1-6],即首先对信号的时域、频域信息进行特征参数提取,随后利用神经网络[1-3]、支持向量机等[4-6]分类器进行分类。近年来,利用信号间统计似然特征的差异进行分类的最大似然方法也逐步得到重视[7-9]。基于特征的方法需要根据所判别的信号种类采用实现最佳可分性的特征值,其最优特征随着信道变化而不同,人工选择工作量大;同时,所处理的信号内部可能存在特定的联系,这些深层次特征不易被参数化描述。基于最大似然方法在使用时需要完整的信道先验信息,但实际情况中往往难以取得;同时,该方法须假设信号先验符合均匀分布[5],局限性大。近年来,深度学习技术作为神经网络技术的最新发展,在图像、语音识别领域获得了广泛应用,其核心思想在于使用新的算法、网络结构提升神经网络的泛化能力,基于深度学习的神经网络能够自动进行特征学习,由于实现了分层特征抽取,反映了数据本身的结构,深度学习在大多数场景下表现优于手工特征提取。基于此,本文研究利用信号时频图对通信调制信号进行分类,将通信信号分类问题转化为图像分类问题,并使用基于深度学习技术的卷积神经网络取代浅层学习结构,通过卷积核对二维数据的纹理信息与空间结构进行特征提取,捕捉不同调制方式在时频图上的微小差异,从而实现信号分类。
1 基于时频图差异的信号调制方式分类
当前,基于人工设计特征参数和浅层学习的信号分类方法获得了广泛应用,即通过人工分析并确定信号分类所需要的特征参数,将信号映射至特征空间,再使用SVM、ANN等分类器进行处理。但是,基于信号瞬时幅度、频率、相位信息的识别方法易受信道的影响,在低信噪比下效果差;而基于高阶统计量的处理方法难以区分QAM信号,必须借助循环谱进一步处理,而循环谱的运算量大,目前还难以实时计算[10]。
时频图分析是一种基于短时傅里叶变换(STFT)的常用人工辅助通信信号分析手段,即通过观察、判别时频图在频点、包络和结构上的差异区别各类信号。时频图能够反映非平稳信号时间、频率和功率之间的关系,其中时间和频率的最小分辨率组合为一个矩形,称之为时频原子。但部分调制方式的差异难以通过图像结构信息体现,不能利用时频图直接观察得到。图 1a)的2FSK信号存在2条高能量谱线,易于识别,但图 1b)、图 1c)中的QPSK、8PSK信号则难以观察区分,这是由于人眼观察时频图时,总是更为注意时频图在结构、轮廓上的差异,而高阶调制的频带掩盖了时频原子的潜在分布差异,难以体现信号内部变化规律。
深度学习中的卷积神经网络(CNN)能够学习、利用图像在多个尺度上的基本结构,这一特性与时频图的多尺度特性匹配。因而,使用CNN对时频图的纹理和结构关系进行学习,就能够确定信号所属的调制方式,为探讨利用纹理信息分类的可行性,本文首先利用灰度共生矩阵[11]、图像局部二值模式[12]来描述时频图的纹理信息,并说明了这些图像特征与信号特征的映射关系。
 |
1 不同调制方式时频图图样 |
1.1 基于时频图特征参数分类方法及其局限性
1) 灰度共生矩阵
灰度共生矩阵反映了图像灰度分布关于方向、变化幅度和局部领域的综合信息[13]。其定义为在θ方向上, 相隔距离d的一对像素分别具有灰度值i和j出现的概率, 记为P(i, j, d, θ), 利用灰度共生矩阵可以得到4类特征参数:
(1) 角二阶矩C1
式中,L为图像最大灰度, 下同。
(2) 惯性矩C2
(3) 逆差分矩C3
(4) 熵C4
2) 图像局部二值模式
图像局部二值模式(LBP)是一种用于描述图像局部纹理特征的方法[14-15]。设图像I尺寸为(a, b), I上有点P(x, y), 在以P为中心的3×3窗口内, 以P灰度为阈值, 将另外8个像素的灰度值与P进行比较, 若灰度值大于P灰度值, 则该点被标记为1, 否则为0。这样, 3×3窗口内的8个点经比较可产生8位二进制数, 即得到该窗口中心像素点的LBP值, 并最终生成一个(a-1, b-1)大小的LBP谱, 其值域为0~255。
本文选择d取[1,4], θ取0°, 45°, 90°, 135°下的灰度共生矩阵统计量, 和图像LBP谱直方图构成联合特征用于分类。由于联合特征维数为320, 因此使用了稀疏自编码器(SA)进行降维, 得到了128维的联合特征, 它保留了原320维特征的全部信息。
从实验中可以看到, 对于2FSK, MSK信号, 基于时频图纹理特征的分类方法有良好的效果, 但对QPSK, 8PSK和256QAM, 1 024QAM信号则不能分辨。本文认为原因在于:
1) 图像的特征统计量不能反映图像特征的组合特性。对于LBP而言, 如图像纹理具有较多的特征模式x, 则LBP直方图x对应二进制数处会出现较高的峰值, 该峰值仅仅显示了x的统计特性, 对于该特征出现的位置、特征间的组合关系则不能体现, 同理灰度共生矩阵也存在相同的问题。
2) 模型维数过高。由于不能事先确定最为有效的特征参数, 算法保留了全部特征, 可能导致冗余信息对最优特征构成稀释。
在图像处理中, 纹理体现的是物体在空间分布的规律及相关性[16], 人工设计的纹理特征参数具有对其空间意义的描述, 而时频谱图中的纹理特征是时间序列映射至高维空间的信息奇异性表征, 而利用灰度信息的纹理特征提取方法难以在高维空间对其描述[17], 且易受噪声影响, 因而效果较差。因此, 本文采用基于卷积神经网络的深度学习方法, 通过高维空间抽取来获取信号的纹理特征, 再通过降维实现不同调制信号的分类。
基于时频图纹理特征的分类实验结果准确率
1.2 卷积神经网络
卷积神经网络(CNN)是一种专门用于处理具有矩阵结构数据的神经网络, 其与普通神经网络的主要区别在于CNN使用由卷积层和池化层(降采样层)构成的特征提取器, 每个卷积层包含多个特征图, 特征图内的单元共享权值以实现参数稀疏[18]。CNN模仿人眼处理信息的分层方式, 利用卷积操作以获取不同尺度卷积核对图像某一区域的激活响应, 实现分层特征提取, 从而使网络反映数据的本质结构。
研究表明, 图像可以分为由不同方向线性函数所描述的边缘[11-12], 将这些二维线性函数组成的矩阵称为图胞, 如图 2所示。
对任意一个图胞P, 将其视为坐标(x, y)的函数, 记为P(x, y), 则任意一个复杂二维图像I可表示为各图胞的加权和, 记权重为w(x, y), 则有
一般情况下, w(x, y)具有Gabor函数的性质, 此时另记w(x, y)为
式中
α, βx, βy, f, ϕ, x0, y0, τ为参数, 这些图胞是图像在不同尺寸上的切分的组成元素, 即小尺度特征的加权和构成大尺度特征。这些大尺度特征同样可以构成更大尺度的特征, 从而形成多层结构。根据图像切分得到的特征不是依靠人工确定的算法得到的特征值, 而是图像本身的结构信息, 因而能够学习时频图纹理信息的最优特征[19], 如图 3所示。
具体学习方法为:
步骤1 随机生成卷积核及各卷积核权值, 并使用这些核对图像进行二维卷积操作, 可以得到图像某一区域对卷积核的激活值, 随后将激活值通过ReLU激活函数处理, 以避免传统网络结构可能出现的梯度消失问题;
步骤2 对激活值进行池化, 即降采样, 从而赋予卷积核对于微小形变、噪声的不变性, 降采样后的激活值作为下一层的输入。
步骤3 将分类输出误差利用反向传播分摊至各层权值, 进行调整, 最终完成各个尺度上卷积核权值的训练。
 |
图2 由Gabor权值描述的图胞 |
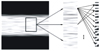 |
3 图像分层切分示意 |
1.3 识别算法设计
1.3.1 信号分类方法
本节利用卷积神经网络提取通信信号时频图纹理特征, 并使用SOFTMAX分类器进行分类, 分类使用欧氏距离损失函数
式中, l为信号样本的输出, y为样本标签, 其具体步骤为:
步骤1 时频图生成与标记。训练开始时, 利用信号样本生成时频图, 并根据对应的调制方式进行标记。为减少STFT带来的纹波, 将时频图进行自适应幂函数增强[20], 使得其带外部分能量降至频带内-30 dB以下。
步骤2 无监督的图像特征提取。使用随机初始化的卷积核检测图像的纹理, 构成特征。
步骤3 有监督的参数微调。将网络输出接入SOFTMAX分类器, 得到所属类别, 并与信号标签进行对比, 将误差向后传递并调整权值。误差下降至满足终止条件时, 在测试集验证网络准确性, 即可得到目标网络。
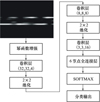 |
图4 信号识别算法流程 |
1.3.2 神经网络参数确定
目前学界普遍认为CNN卷积核的大小决定了CNN的特征提取能力, 因而必须确定卷积核的大小使其能够观察到图像在纹理、结构上的区别。本文认为小尺度卷积核应当能够覆盖时频原子, 使得一个小尺度卷积核匹配一个FFT单元, 下面对其尺寸与FFT参数进行分析, 试图确定其大小。
假设样本信号S(t)采样率为Fs, 码元速率为Rb, 时长为T, 则总长度为T·Fs点; 在进行n点长STFT后生成时频图长度为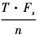 点, 每个时频原子包含
点, 每个时频原子包含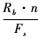 个码元; 在奈奎斯特采样下, 最高频率为
个码元; 在奈奎斯特采样下, 最高频率为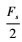 , 频率分辨率为
, 频率分辨率为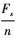 , 则共有
, 则共有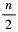 点; 最终形成时频图的尺寸为
点; 最终形成时频图的尺寸为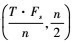 , 随后将其缩放至(L, L), 假设卷积核按层由上到下大小分别为(x, x), (y, y), (z, z)。本文中, 为限制问题复杂度, 确定以3个时频原子组成一个卷积核, 即z取3, 此时有
, 随后将其缩放至(L, L), 假设卷积核按层由上到下大小分别为(x, x), (y, y), (z, z)。本文中, 为限制问题复杂度, 确定以3个时频原子组成一个卷积核, 即z取3, 此时有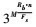 种时频原子组合, 将其视为16个卷积滤波器加权和, 即卷积核参数为(3, 3, 16)。
种时频原子组合, 将其视为16个卷积滤波器加权和, 即卷积核参数为(3, 3, 16)。
其他2层参数确定尚无数学根据, 现由多次实验确定x取32, y取8。第一层共4个过滤器, 第二层为8个, 第三层16个。
2 实验验证
为验证方法的有效性, 本文设计了包含2FSK, MSK, QPSK, 8PSK, 256QAM, 1 024QAM 6种调制方式在内的六分类实验, 观察分类效果, 并借助卷积核梯度图像分析核特性。
2.1 信号样本设计
实验中为去除其他因素的影响, 采用随机生成的0, 1比特, 经调制生成采样率Fs为10 MHz、符号速率R为1 M波特的信号, 信号共计10 000点, FFT窗长取1 024。
对于2FSK, MSK, QPSK, 8PSK, 256QAM, 1 024QAM信号, 其载频Fc取2 MHz, 第一零点带宽2 MHz, 2FSK信号的Fc1取2.2 MHz, Fc2取1.8 MHz, 并生成时频图, 每组随机数对应生成6个时频图样本, 并全部缩放至128×128, 共生成24 000个样本, 如图 5所示, 图 5a)~5f)分别为2FSK, QPSK, 8PSK, MSK, 256QAM, 1 024QAM信号。从中取3 600个样本作为测试集, 另外20 400个样本作为训练集。
 |
5 时频图样本 |
2.2 调制样式分类实验
本文在实验中, 将训练集信号样本组成尺寸为(128, 128, 20 400)的矩阵导入神经网络, 待网络训练完毕后对测试集中的图像进行分类测试。实验共进行5次, 结果取平均, 保留1位小数。为体现效果, 这里同时采用文献[2-4]方法作为对比。
文献[2]中, 使用信号的奇异谱、功率谱、小波能量谱熵特征作为特征参数输入SVM进行分类。
文献[3]中, 使用了信号的高阶原点矩和高阶累积量构成17维联合参数, 输入多层感知机(MLP)进行分类, 该MLP共3层, 单元数分别为20, 8, 6。
文献[4]中, 将信号高阶统计量|C61|2/|C42|3和平滑后的频谱相关峰值作为特征参数, 输入SVM分类器进行分类。
为体现图像非线性增强的有效性, 同时对比增强前后效果, 记录准确率如表 2所示。可以看到, 本文算法具有良好的分类能力, 在进行幂函数增强且信噪比为0 dB时, 仍能得到89.1%的准确率, 较基于特征值的方法提升约7%, 而在信噪比为6 dB以上时准确率可达99%, 且本文算法仅涉及对信号中心频率的估计, 减少了人工设计特征参数的工作量。
一般而言, 神经网络的学习过程难以观察, 为了解释网络学习成果, 本文采用梯度图像诊断网络参数, 即导出网络中某个给定层对于输入图像的梯度, 随后将其缩放, 使其与输入大小保持一致并与输入图像叠加, 再次作为输入; 如此反复迭代多次, 使得最终输出反映该核的特性。
图 6为卷积层1生成梯度图像。由于卷积层1的核尺寸较大, 因而卷积运算对图像形成平滑, 弱化了纹理的影响, 主要关注信号在频谱图中的位置。可以看到, 卷积层1获取了信号高能量部分(图像中心)。
卷积层2尺寸减小, 使得各滤波器进一步反映了信号结构信息。从图 7中可以看到, 该层提取了时频图的上下边缘, 由于时频图不是恒包络的, 因而边缘不平整, 另外, 由于卷积核较大, 该层仍然不能提取纹理信息。
随着卷积核进一步减小至能够与时频原子大小相比拟时, 能够反映图像时频原子的特性, 观察提取的纹理信息可以发现, 生成图像的高能量部分存在偏移, 即卷积核对中频偏移不敏感。
图 9为全连接层生成梯度图像, 全连接层获取与其匹配的纹理, 并将其放大, 可以观察到图像中低能量部分存在简单图案的重复, 这是由卷积核激活值最大的部分生成图像叠加在输入的低能量区上形成的图案, 因而消除了输入信号能量的影响, 换言之, 即神经网络认为各类时频图是由这些简单图案构成的, 可以认为神经网络成功提取了纹理特征, 并成功区分了这些从时频图结构特征上无法区分的信号类型。
分类准确率数据
 |
图6 卷积层1生成梯度图像 |
 |
7 卷积层2生成梯度图像 |
 |
图8 卷积层3生成梯度图像 |
 |
9 全连接层生成梯度图像 |
2.3 扩展类别识别
为了验证方法对更多调制方式的适应性, 本文还进行了包含2FSK, 4FSK, MSK, BPSK, QPSK, 8PSK, 8QAM, 16QAM, 64QAM, 256QAM, 1 024QAM信号在内共计11类信号的调制识别实验。
由于高阶PSK调制的抗干扰性能较差, 实际应用中很少使用16及以上进制的PSK调制, 出于同样的原因也不使用1 024以上进制的QAM调制。在实验之前, 可以联想到8QAM和8PSK的星座图接近, 各相位上的幅值差别较小, 当在8个相位上具有相同的符号映射时难以分清, 因此首先进行8QAM和8PSK类别分类实验以验证适应性。信号参数、神经网络网络设计同2.1节一致, 2类各提供4 000个时频图样本作为训练集, 另外各200个作为测试集。测试结果如下(保留1位小数, 实验进行5次, 结果取平均值)。
可以看到二分类结果较差, 算法不能有效区分8QAM和8PSK信号。但考虑到8QAM和8PSK信号解调方法没有大的区别, 接下来的实验中将把8QAM, 8PSK作为一类进行处理。对于2FSK, 4FSK, MSK, BPSK, QPSK, (8PSK, 8QAM), 16QAM, 64QAM, 256QAM, 1 024QAM共计10类信号, 信号参数、神经网络设计同2.1节一致, 每类各提供10 000个样本作为训练集, 另外各200个作为测试集。测试结果如下。
结果表明, (1)在分类数量增加时, 分类性能出现了一定下降, 算法仍能保持精确度在70%以上。(2)在信噪比小于等于4 dB时, 幂函数增强不起作用, 此时应当关闭增强特性。
本文算法分类准确率数据
分类准确率数据
3 结论
本文针对信号调制方式分类问题中基于特征参数的机器学习方法的缺点, 提出利用信号时频图将一维信号分类问题转化为二维图像分类问题, 解释了二维图像特征参数和一维信号特征参数之间的映射关系, 并针对基于特征参数的图像分类对信号时频图的不适应性, 提出使用CNN提取图像特征, 将特征参数反映在网络参数内, 并将其用于信号分类, 实验中, 对2FSK, MSK, QPSK, 8PSK, 256QAM, 1 024QAM信号的分类取得了较好的结果, 证明了其相对传统方法的优越性。下一步的工作中, 可以对神经网络结构进一步调整, 使其具有识别训练集以外样本的能力, 由于数字调制种类有限, 因而可以尝试利用信号的进制数、频点数、中心频率、频偏等特征参数的集合G完成对某一信号调制方式的语义描述, 这个语义描述可以代替人工标注的标签。此时, 可以将神经网络定义为3层模型, 第一层为本文所描述的3层CNN, 第二层为一个n参数的分类器, 用于判断CNN输出和G的对应关系, 第三层为一个语料库, 根据n个参数将信号映射到具体类别, 从而实现在无样本情况下的零样本语义识别。
References
- Chen Hong, Cai Xiaoxia, Xu Yun, et al. Communication Modulation Recognition Based on Multi-Fractal Dimension Characteristics[J]. Journal of Electronics and Information Technology, 2016, 38(4): 863–869 [Article] (In chinese) [Google Scholar]
- Yang Faquan, Li Zan, Li Hongyan, et al. Research of Communication Modulation Recongnition Based on Bee Colony Algorithm and Neural Netowork[J]. Systems Engineering and Electronics, 2013, 35(10): 2186–2191 [Article] (In chinese) [Google Scholar]
- Li Yibing, Ge Juan, Lin Yun. Modulation Recongition Using Entropy Features and SVM[J]. Systems Engineering and Electronics, 2012, 34(8): 1691–1695 [Article] (In chinese) [Google Scholar]
- Zhao Xiongwen, Guo Chunxia, Li Jingchun. Mixed Recognition Algorithm for Signal Modulation Schemes by High-Order Cumulants and Cyclic Spectrum[J]. Journal of Electronics & Information Technology, 2016, 38(3): 674–680 [Article] (In chinese) [Google Scholar]
- Han Jie, Zhang Tao, Wang Huanhuan, et al. Communication Emitter Individual Identification Based on 3D-Hibert Energy Spectrum and Multi-Scale Fractal Features[J]. Journal on Communications, 2017, 38(4): 99–109 [Article] (In chinese) [Google Scholar]
- Nandi A K, Azzouz E E. Algorithms for Automatic Modulation Recognition of Communication Signals[J]. IEEE Trans on Communications, 1998, 46(4): 431–436 [Article] [CrossRef] [Google Scholar]
- Fu Junqiang, Li Rong, Zhao Chenglin, et al. Sequential Bayesian Inference Based Adaptive Modulation Recognition Algorithm[J]. Systems Engineering and Electronics, 2015, 37(12): 2860–2864 [Article] (In chinese) [Google Scholar]
- Liu Mingqian, Li Bingbing, Cao Chaofeng, et al. Recognition Method of Digital Modulation Signals over Non-Gaussian Noise in Cognitive Radio[J]. Journal on Communications, 2014, 35(1): 82–88 [Article] (In chinese) [Google Scholar]
- Lu Shanshan, Wang Wei, Wang Guoyu. Constellation Recovery and Modulation Recongition for Multiplequadrature Amplitude Modulation Signals[J]. Journal of Mational University of Defense Technology, 2016, 38(6): 130–134 [Article] (In chinese) [Google Scholar]
- Swami A, Sadler B M. Hierarchical Digital Modulation Classification Using Cumulants[J]. IEEE Trans on Communications, 2000, 48(3): 416–429 [Article] [CrossRef] [Google Scholar]
- Haralick R, Shanmngam K, Dinstein I. Texture Feature for Image Classification[J]. IEEE Trans on Systems, Manand Cybernetics, 1973, 3(6): 768–780 [Article] [Google Scholar]
- Ji Zhong, Nie Linhong. Texture Image Classification with Noise-Tolerant Local Binary Pattern[J]. Journal of Computer Research and Development, 2016, 53(5): 1128–1135 [Article] (In chinese) [Google Scholar]
- Lee H, Grosse R, Ranganath R. Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations[C]//International Conference on Machine Learning, 2009 [Google Scholar]
- Lee Y J, Grauman K. Learning the Easy Things First: Self-Paced Visual Category Discovery[C]//Conference on Computer Vision and Pattern Recognition, 2011 [Article] [Google Scholar]
- Nixon M, Alberto S. Aguado. Feature Extraction and Image Processing[M]. Amsterdam, Elsevier Academic Press, 2008 [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton G. Imagenet Classification with Deep Convolutional Networks[C]//Advances in Neural Information Processing Systems, 2012: 1097–1105 [Article] [Google Scholar]
- Goodfellow I, Courville A. On Distinguishability Criteria for Estimating Generative Models[C]//International Conference on Learning Representations, 2014 [Article] [Google Scholar]
- Kingma D, Rezende D, Mohamed S. Semi-Supervised Learning with Deep Generative Models[C]//Neural Information Processing Systems, 2014 [Google Scholar]
- Bertoncini C, Rudd K, Nousain B. Wavelet Fingerprinting of Radio-Frequency Identification(RFID) Tags[J]. IEEE Trans on Industrial Electronics, 2012, 59(12): 4843–4850 [Article] [CrossRef] [Google Scholar]
- Sun Yankui. Wavelet Analysis and Application[M]. Beijing, Mechanical Industry Press, 2005 (In chinese) [Google Scholar]
All Tables
All Figures
 |
1 不同调制方式时频图图样 |
| In the text | |
 |
图2 由Gabor权值描述的图胞 |
| In the text | |
 |
3 图像分层切分示意 |
| In the text | |
 |
图4 信号识别算法流程 |
| In the text | |
 |
5 时频图样本 |
| In the text | |
 |
图6 卷积层1生成梯度图像 |
| In the text | |
 |
7 卷积层2生成梯度图像 |
| In the text | |
 |
图8 卷积层3生成梯度图像 |
| In the text | |
 |
9 全连接层生成梯度图像 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


