EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 345-356 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 345 - 356
DOI https://doi.org/10.1051/jnwpu/20254320345
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

超视距空战远距离接敌导引是根据目标的位置、速度和姿态等信息, 导引战斗机沿合适的轨迹以较优的姿态去跟踪、接近或拦截目标。

比例导引(proportional navigation, PN)是最早出现的导引律, 它通过抑制视线旋转来实现跟踪制导[1], 具有形式简单、便于工程实现等优点, 但当目标机动过快时, 传统PN的制导性能会大幅下降, 且制导过程无法考虑其他约束条件。为解决制导过程中需要约束的问题, 国外的Kim等[2]通过设计与剩余飞行距离相关的时变偏置项, 利用偏置比例导引律(BPNG)实现了制导末段的进入角约束; 在此基础上, 文献[3]设计了一种满足任意初始前置角和末端攻击角度约束的偏置比例导引律, 解决了前置角变化较大的问题。针对目标机动时制导精度不高的问题, 文献[4]中提出了一种基于扩展比例导引律的制导模型, 将目标的加速度作为补偿值, 在传统比例导引律上对加速度、重力的影响及目标机动的影响进行补偿, 该方法提升了导引制导的机动能力和效率; 在此基础上, 文献[5]基于泰勒级数预测模型对加速度的修正项进行迭代控制, 提出了一种改进的比例导引律, 仿真表明该方法进一步提高了制导的精度; 文献[6]则提出一种基于反向传播神经网络的自适应偏置比例导引律, 在证明参数和偏置项之间存在映射关系的基础上, 采用BP网络对该映射进行高精度的拟合逼近, 提高了偏置比例导引的制导精度。

微分对策导引律的优势是仅需获知目标的机动性能，Sun等[7]将其描述为受不确定因素影响的零和微分博弈问题, 采用自适应动态规划算法并利用修正网络求解HJI(Hamilton-Jacobi-Isaacs)方程, 得到了良好的制导拦截效果。在此基础上, 文献[8]提出了一种基于双启发式的自适应动态规划算法, 将视线角速度作为回报, 求解出了一种更加平稳的制导方法。文献[9]提出了双导弹以角度协同方式拦截目标的微分对策律, 降低了对导弹加速度性能的要求; 文献[10]进一步考虑了多弹协同的场景, 提出了一种基于微分对策的协同制导方法, 该方法综合考虑二维空间内的多种约束条件和导弹间的信息交互问题, 得到了多弹协同微分对策导引律, 并通过仿真证明了协同导引律的有效性。

最优导引律是基于最优控制理论研究出的导引律。假设机动目标的运动信息是完全可观的前提下, 文献[11]推导出了导弹制导过程中的最优导引律。最优导引律不仅能够考虑导弹-目标的动力学问题[12], 而且可以考虑制导起点或终点的约束条件, 例如终端脱靶量、可控时长等。针对最优控制律捕获时长不足的问题, 可将滚动时域控制(receding horizon control, RHC)应用到最优控制律中, 来克服计算捕获时间的困难[13]。然而, 最优控制律依然要求目标运动轨迹完全已知, 这在实际空战中几乎是不可能的, 因此实用性不强。

基于现代控制理论设计的导引律可以提高导引算法在各种不确定因素条件下的有效性和鲁棒性。文献[14]利用李雅普诺夫优化法对导弹控制系统进行反馈, 提出了一种非线性导引律, 其计算控制量时无需测出目标线角速度和目标加速度。文献[15]中设计了一种滑模导引律, 它不需要准确的目标加速度, 但要得到目标机动的上界。

近些年随着各类搜索优化算法的发展, 许多学者开始研究将这些搜索算法应用到导引领域, 将对战斗机的导引问题视为动态的航迹规划、机动决策问题, 通过迭代搜索寻找每一时刻的最优导引指令。例如, 文献[16]采用模糊控制原理, 将火控系统距离和方向上的瞄准误差转化为飞机的控制指令, 实现了火控的攻击导引; 文献[17–19]分别利用粒子群算法、遗传算法和强度学习实现了无人机航路的实时规划导引; 文献[20–22]分别利用LSTM网络、蒙特卡洛树搜索法和强化遗传算法实现了无人机的机动占位。

上述对战斗机的各种导引方式分别在导引的精确度、时效性、鲁棒性等方面有着各自的优势。然而这些方法大都将载机-目标视为2个质点的相对运动, 未考虑空战双方RCS变化对导引精度和导引方式的影响。实际进行远距接敌导引的过程中, 由于双方相对位置和目标姿态的实时变化, 我方机载雷达入射方向的目标RCS可能发生剧烈变化, 这将直接影响雷达对目标的探测概率。机动性能和隐身性能较好的目标便能借此摆脱跟踪, 给载机的远距接敌导引增添极大的不确定性。因此, 在充分考虑目标RCS动态变化的影响下制定载机的导引策略, 可以使跟踪过程中的目标RCS保持在较大的区间内, 提高机载雷达探测和跟踪的稳定性, 减小导引过程中目标丢失的概率。

1 算法模型与流程

建立基于动态RCS约束的超视距空战导引算法, 首先通过分析导弹攻击区、目标威胁区和目标全空域RCS的分布规律, 研究战机远距接敌导引的最佳攻击态势; 其次建立远距接敌导引时的三维空间内载机-目标相对运动模型, 并由此推导出考虑目标RCS约束的空战态势评估模型; 最后研究基于粒子群过载寻优的载机导引策略, 并在此基础上考虑动态RCS约束, 建立从攻击占位、攻击区解算到导弹制导的全流程模型。

1.1 基于动态RCS的最佳态势分析

1.1.1 基于RCS约束的攻击态势分析

当载机距离目标较远且尚未发射导弹时, 远距接敌导引的目的是导引我方战机快速接近目标, 抢占可攻击的优势位置, 形成可以发射导弹的最佳态势。因此, 远距接敌导引的末端区域应与载机所搭载的武器性能相关, 应参考空空导弹的可攻击区来确定。最佳攻击态势需要从以下3点来考虑:

1) 从战术进攻角度考虑, 为保证导弹发射后具有较高概率命中目标, 最佳攻击占位点应处于我方导弹可攻击区内, 且我机要对准目标(满足离轴角要求)。

2) 从战术防御角度考虑, 为增加我方的生存概率, 攻击占位点应尽量避开目标的可攻击区范围或目标雷达的可探测范围。

3) 从雷达探测概率角度考虑, 为尽可能地避免目标丢失问题, 攻击占位点方向上的目标RCS要尽可能的大。

根据上述3点, 可综合考虑我方空空导弹的可攻击区, 目标的威胁区以及目标的RCS数据分布来求解最佳攻击态势, 如图 1所示。

图 1为目标直线飞行时, 目标所在水平面内的最佳攻击态势分析图。图 1中蓝色区域为目标的威胁区, 即目标探测区域和目标可攻击区的重叠部分; rT, ϕT分别为扇形威胁区的半径和圆心角; 2个椭圆分别为以目标为中心的可攻击区的内外边界; 目标战斗机周围的曲线反映了RCS(单位为dB)随雷达入射方位角的变化趋势; 2个红点即为考虑动态RCS约束的最佳占位点, 位于目标机体两侧。当我方战机位于最佳占位点且满足最小离轴角时, 处于最优的攻击态势。

选取占位点时, 假设在远距接敌导引过程中目标尚未发现我方战机, 处于巡航阶段, 因此可近似认为目标侧滑角为零。此时目标的航迹偏转角ψc_T和偏航角ϕT一致。根据目标RCS和雷达入射方位角ϕ的关系可知, 当机载雷达位于目标机体两侧(即ϕ≈90°或ϕ≈270°)时, 目标的RCS值往往较大, 雷达瞬时探测概率更高。图 1中红色占位点既满足导弹发射的攻击区内外边界要求, 又避开了目标的威胁区, 且此处载机正好位于目标的正侧方, 目标的RCS处于最大值, 有利于对目标的探测和跟踪。

综上所述, 本文选取攻击区外边界上目标进入角为90°或270°的位置作为最佳占位点, 当我方战机位于最佳占位点且满足最小发射离轴角时, 处于最优的攻击态势。

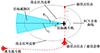thumbnail 图1

最优攻击态势分析图

1.1.2 最佳占位点仿真

目标不同机动、不同初始状态下的攻击区边界都是不同的。在考虑动态RCS约束时(设探测概率下限Pmin=0.5), 在目标执行水平急转弯和置尾机动时进行最佳占位点仿真。得到载机的最佳占位点如图 2~3所示。

图 2~3中, 红点为本文认为的远距接敌导引最佳占位点。可以看出, 目标不同机动下的占位点不同, 同一机动下的2个占位点也不同。实际进行远距接敌导引时, 载机只需选择距离战机最近的占位点最为目标点即可。

thumbnail 图2

占位点-水平急转弯
thumbnail 图3

占位点-置尾机动

1.2 基于动态RCS的态势评估模型

本节首先对一对一远距接敌导引的空战态势进行建模, 之后在传统态势评估基础上, 考虑目标RCS动态起伏对远距接敌导引的影响, 调整了角度评估方法, 并增加了对雷达探测概率的评估，期望导引载机往目标RCS值较大的最佳占位点飞行。

1.2.1 远距接敌导引的态势建模

空战态势是用来描述敌我飞机相对位置、相对速度和相对角度等信息的一个向量, 也是判断目标当前的威胁程度和敌我双方位置优劣的基础。空战态势包含的信息越全面越精确, 描述的空战情景就会越完整, 所做出的判断就更趋近于最优策略。但同时, 过于庞大的信息量也会降低决策的速度, 影响决策的时效性。合理的态势评估模型不仅可以准确描述当前的空战情景, 确保决策结果的可靠性, 还可以减小相关的计算量。因此, 在远距接敌导引时, 要建立合适的空战态势评估模型。在三维空间内, 一对一的空战态势如图 4所示。图 4中, 在北天东坐标系下, P(xP, yP, zP), T(xT, yT, zT)分别为载机和目标的位置坐标; vP, vT分别为载机与目标的速度; θP, ϕP分别为载机的航迹倾斜角以及航迹偏转角; θT, ϕT分别为目标的航迹倾斜角以及航迹偏转角; r为载机-目标连线的矢量, rxz为其在XOZ平面上的投影; θr, ϕr为目标视线的俯仰角以及偏转角; ϕ, q分别为我机的偏离角与目标的进入角(两者速度矢量与目标相矢量间的夹角, 取值范围均为[0°, 180°])。

图 4中, 目标线r在北天东坐标系下3个坐标轴上的投影分别为rx, ry, rz, 则有

式中, rx=xT-xP, ry=yT-yP, rz=zT-zP, rxz=。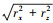

我机的偏离角和目标的进入角可根据向量运算公式求解，如(2)式所示。

式中：vPx, vPy, vPz分别为我机速度在3个坐标轴上的投影分量; vTx, vTy, vTz分别为目标速度在3个坐标轴上的目标速度投影分量。

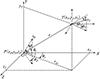thumbnail 图4

远距接敌导引态势

1.2.2 基于RCS约束的态势评估

空战优势函数是评估当前态势优劣的标准, 根据1.2.1小节对远距接敌导引态势的建模, 本文将从角度、距离、高度、速度和基于动态RCS的雷达探测概率五方面设置评估子函数对空战态势进行评估[20]。

1) 考虑RCS约束的角度评估子函数f1

我方战机与敌方战机之间相对角度的优劣与我机的偏离角和目标的进入角有关。角度评估函数的作用是导引我方战机调整航向, 以合适的目标进入角进入导弹可攻击区域, 并能以合适的离轴角发射导弹。图 5反映了远距接敌导引中载机-目标间的相对角度关系, 其中图 5a)描述了载机-目标在三维空间内的角度关系, 图 5b)分别将目标线矢量和目标速度矢量投影到目标所在的水平面内, 得到了目标的水平进入角qxoz。

图 5中, ϕ为我机偏离角; r为目标线矢量, rxoz为目标线矢量r的水平投影; q为目标进入角, qxoz为水平进入角, 取值范围[0°, 180°]; vT_xoz为目标速度矢量vT的水平投影。

对于目标进入角而言, 近距离“狗斗”的机动决策中一般认为尾追优势(目标进入角q→0°)最优[20]。因为当敌我双方距离较近时, 形成尾追优势后载机跟踪目标所需要的转弯过载最小, 更容易保持对目标的跟踪。然而, 本文考虑的远距接敌导引场景下敌我距离相对较远(通常距离d>60 km), 跟踪目标时需要的转弯过载并不高。因此, 在研究目标自身角度对态势的影响时, 本文着重考虑目标RCS对探测概率的影响。根据1.1.2小节对占位点的分析可知, 在忽略侧滑角的情况下, 当目标水平进入角qxoz=90°时RCS处于最大值, 雷达的探测概率相对较大, 此时认为较优; 当qxoz=180°时, 我方战斗机有被目标探测和锁定的风险, 认为此时态势较差。因此, 目标进入角q的优劣一定程度可以通过水平进入角qxoz的大小进行反映, 本文对目标进入角的评估函数为

式中, ϕT为目标扇形威胁区域的最大角度。

对于我机偏离角而言, 本文认为当偏离角ϕ→0°时为最优态势。此时我方战机朝着目标迎头飞行, 不仅能快速地接近目标, 还可以充分发挥我方机载雷达的性能，实现对目标的探测和跟踪。此外, 当携带导弹的离轴角较小时, 迎头飞行也能为战斗机创造良好的开火条件。因此我机偏离角评估函数为

综上所述, 本文的角度优势函数由进入角函数fq和偏离角函数fϕ相乘, 得到角度方面的评估子函数f1如(5)式所示。

2) 距离评估子函数f2

空战中, 载机与目标之间的距离对态势的评估起着重要作用, 一方面, 机载雷达的瞬时概率受到相对距离的影响; 另一方面, 导弹的制导成功率也与导弹-目标初始距离息息相关。距离评估函数的主要作用是导引我方载机迅速逼近目标, 进入攻击区范围内达成导弹发射条件。本文通过敌我战机间距d衡量距离优势, 定义距离评估子函数f2为[23]

式中：dq为对应目标进入角下的攻击区外边界; dradar为目标RCS处于较大值时, 我方机载雷达最大探测距离。

3) 高度评估子函数f3

根据空战经验, 当载机具有合适的高度优势时, 可攻击区往往会变大, 对导弹制导而言, 适当的高度优势同样使导弹具有更多的势能, 将其转换成动能可增大导弹的最大可控航程。当然, 载机的高度优势不能过大, 一方面高空稀薄的空气会对飞机的飞行造成负面影响; 另一方面, 载机-目标间高度差过大会使目标视线俯仰角过大, 不利于导弹发射。

综合来讲, 在合适的范围内, 战机对目标具有一定的高度优势对空战的影响是正面的, 高度优势应由我方高度hP和目标高度hT共同决定, 本文高度评估子函数f3设置为[24]

式中：h0为最佳高度；hT为目标飞行; 高度hmin为载机可飞行的最小高度。

4) 速度评估子函数f4

空战中, 速度较快的战机往往更具有空战的主动性和优先权, 根据具体态势选择逼近目标进行攻击或拉开距离摆脱敌方的跟踪。对于远距接敌导引来说, 当战机-目标距离较远时, 应该导引我方战机加速靠近目标; 当我方逐渐逼近可攻击区范围时, 由于速度过快会导致转弯半径过大、最佳攻击时间间隔过短等问题, 此时应该适当地减小速度, 期望与目标相近, 为导弹发射创造条件。综合考虑以上因素, 本文的速度优势函数与最佳空战速度v+有关, 如(9)式所示。

式中：vT为目标的速度; v+为最佳空战速度。本文的速度评估子函数f4如(10)式所示。

5) 考虑目标RCS的探测概率评估子函数f5

上述对空战态势中相对角度、相对距离和相对高度的评估可以导引我方战机朝着最佳占位点飞行, 在目标RCS相对较大的位置发射导弹。然而, 目标RCS随雷达入射角的变化是随机的、上下抖动的。在飞行过程往往会遇到目标RCS突然变小的情况, 将导致雷达的瞬时探测概率大大降低, 容易造成目标丢失。因此, 本文考虑目标RCS的起伏对雷达瞬时探测概率的影响, 假设目标飞行过程中的姿态角信息我方全部可知, 将雷达的探测概率作为态势评估的一个指标, 定义雷达探测概率评估子函数f5如(11)式所示。

式中: Pdr为机载雷达对目标的瞬时探测概率, 可根据雷达瞬时探测概率公式计算; Pdr_min为满足目标跟踪的要求的雷达最小瞬时探测概率。

5个态势评估子函数, 可以从5个不同的维度对空战态势进行评估, 实际空战中需要综合考虑各个方面的影响来进行远距接敌导引。本文采用线性加权的方式得到最终的态势评估函数

式中: w1, w2, …, w5为各个子评估函数的权重系数, 满足

在远距接敌导引中, 要根据不同阶段态势合理地调整各个权重系数。在远距接敌导引初期双方的距离较远, 此时应适当增大距离和角度优势, 使我机从合适的角度迅速逼近目标; 在远距接敌导引中期, 当我方战机位于目标侧方qxoz≈90°时, 应适当增加高度优势使载机-目标尽快处于同一高度范围; 在远距接敌导引后期, 当角度优势较高时, 提高速度权重使我机以合适的速度跟踪目标, 为进入攻击区进行导弹发射做准备。

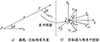thumbnail 图5

相对角度关系示意图

1.3 基于粒子群算法的过载寻优算法

远距接敌导引的过程实际上是导引己方载机前往最佳占位点, 不断提高空战优势的过程。本文中我机的运动迭代使用三自由度的控制模型, 利用过载n=(nx, ny, nz)来控制飞行。因此, 远距接敌导引问题的重点在于如何找到每一空战时刻的最佳过载控制量, 使得我方战机的空战态势能不断提高, 快速接近占位点。

粒子群优化算法(particle swarm optimization, PSO)是一种模拟鸟群觅食行为的非线性极值寻优算法, 可用于求解模糊控制、多目标优化等问题。算法的核心思想是利用群体中个体对信息的共享, 使整个群体的运动在问题求解空间中产生从无序到有序的演化过程[25], 从而获得问题的可行解。该算法具有原理简单、收敛速度快、设置参数少等优点[26]。

本节基于前文建立的空战态势模型和态势评估函数, 采用粒子群优化算法对远距接敌导引时3个方向上的过载控制量进行寻优搜索, 期望得到每个时刻最佳的过载, 从而导引我机前往最佳占位点, 完成导弹发射前的准备。

1.3.1 基于粒子群算法的单步过载寻优

粒子群算法属于进化算法的一部分, 粒子群中的每一个粒子都代表一个问题的可能解, 通过粒子个体的简单行为, 以及种群内的信息交互实现优化问题的求解。远距接敌导引中我方战斗机的最佳过载控制量n =(nx, ny, nz)可以通过粒子群寻优算法得到。

本文将战斗机过载控制量参数的个数作为粒子向量的维度, 随机构造初始粒子群, 群内每一个粒子都代表一组战机过载控制量, 将远距接敌导引中的空战态势评估值fT作为评价粒子的适应度函数, 通过计算粒子适应度得到个体最优解和群体最优解。单个粒子搜索的速度和方向都会根据个体最优解和群体最优解不断更新[25], 粒子状态更新之后继续计算适应度值, 不断循环搜索直至满足收敛条件, 最终得到当前时刻最优的过载控制量, 标准粒子群优化算法的流程如图 6所示。

根据图 6所示的标准PSO算法流程, 本文中粒子群算法寻找最优过载控制量的算法流程如下。

步骤1  初始化粒子群群体

根据我方战机过载控制量未知数的个数确定粒子维度, 随机产生过载控制量粒子的初始位置和速度。设置群体规模为Nc, 最大迭代次数N, 过载控制量粒子维度为3, 随机生成Nc个初始控制量粒子, 每个粒子及其速度分别记为χi和vi(i=1, 2, 3, …, Nc)。

步骤2  计算控制量粒子的适应度值

对于每一个控制量粒子, 将粒子χi代入适应度函数中计算其适应度值。本文根据(12)式的态势评估函数得到适应度函数

若迭代次数达到设定的最大值, 则结束过载控制量搜索, 将种群中适应度值最大的粒子作为全局最优粒子Gbest, 得到最优的过载控制量, 否则继续。

步骤3  更新个体最优解

将第i个过载控制量粒子χi的前适应度值Di与该粒子的历史最优位置χPi适应度值DPi进行比较, 若Di>DPi, 则更新第i个粒子的个体最优粒子为χi, 否则继续。

步骤4  更新群体最优解

将第i个过载控制量粒子χi的前适应度值Di与种群内的历史最优粒子χGi适应度值DG进行比较, 若Di>DG, 则更新群体最优粒子为χi, 否则继续。

步骤5  更新粒子的位置和速度

在更新过个体及群体最优解后, 根据(15)~(16)式更新第i个粒子的位置和速度。速度更新公式为

式中: ω为速度惯性权重；c1, c2为加速度因子常数；r1, r2为[0, 1]上的随机数, 用来增加搜索的随机性。

位置更新更公式为

步骤6  返回步骤2继续迭代。

thumbnail 图6

粒子群算法流程图

1.3.2 单步过载寻优仿真

为验证基于粒子群优化算法过载寻优的有效性, 并确定粒子群算法中相关参数设置的合理性, 本文首先进行了远距接敌导引的单步过载寻优仿真, 涉及的相关算法参数如表 1所示。

以远距接敌导引中某次空战态势为例进行基于粒子群算法的过载寻优, 搜索过程中适应度值的变化结果如图 7所示。

图 7中, 红色曲线反映了群体最优解的适应度值随迭代次数增加的变化趋势, 蓝色曲线反映了种群内所有粒子的平均适应度值随迭代次数增加的变化趋势。为验证粒子群寻优算法在时效性方面的表现, 本文基于某一空战片段, 连续进行了多次单步过载寻优仿真，其运算时间如图 8所示。

如图 8所示共进行了60次的单步粒子群过载寻优仿真, 除去代码刚启动阶段的时间波动后, 其余单次仿真的平均运行时间在43 ms左右。算法可以满足时效性的要求。

表1

粒子优化算法仿真参数

thumbnail 图7

粒子群算法适应度曲线
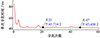thumbnail 图8

过载寻优运行时间

2 仿真分析

在1.3.2节验证了基于粒子群优化算法求解过载控制量的单步可行性, 在此基础上, 本节开展远距接敌导引的仿真，具体过程为: 根据空战态势信息实时计算攻击区, 继而求出导弹最佳发射点; 基于粒子群寻优算法实时计算最佳过载控制量, 导引战斗机前往最佳发射点; 战机到达最佳发射点后调整自身姿态, 使其满足导弹发射条件, 形成适合导弹发射的最优空战态势。远距接敌导引的仿真参数如表 2所示。

分别在2个不同场景下进行远距接敌导引仿真, 当态势评估值F≥0.92认为到达最佳攻击态势, 结束接敌导引。2个场景的初始参数如表 3所示。

2个场景中, 考虑动态RCS约束, 基于粒子群优化算法进行过载寻优的远距离远距接敌导引仿真结果如图 9~10所示。

1) 场景1:目标匀速直线巡航

2) 场景2:目标匀速盘旋

图 9a)和图 10a)为远距接敌导引的3D仿真结果, 图 9b)和图 10b)为相应的俯视图; 红色战机为我方飞机, 其飞行轨迹对应为红色; 蓝色战机为敌方目标, 其飞行轨迹对应为蓝色; 目标周围的绿色曲线为我方空空导弹的可攻击区外边界; 绿点为远距接敌导引的最佳占位点, 处于攻击区外边界附近, 位于目标侧方。

3) 与未考虑RCS的远距接敌导引对比

由于战机-目标间的距离对雷达探测概率有很大影响, 本文选取战机-目标初始相对距离较大的场景1进行仿真, 更能凸显RCS变化对探测概率的影响。当不考虑RCS影响时, 我机采取仍基于粒子群寻优的方式进行导引, 此时空战轨迹如图 11所示。

图 11为忽略RCS约束的远距接敌导引轨迹图, 我方战机最终飞到了目标尾后, 与目标的水平距离满足攻击区发射的要求。将此图与考虑动态RCS约束的图 9进行对比, 两者的初始场景和战机性能完全一致, 仅有导引方式不同。本文从远距接敌导引过程中空战态势、雷达探测概率、目标动态RCS 3个方面进行对比, 结果如图 12~14所示。

图 12所示为远距接敌导引过程中空战态势评估值的变化情况, 不难看出2种算法均可以让我方战斗机的空战态势逐渐变大, 但考虑动态RCS约束的远距接敌导引其最佳占位态势更好, 因此最终态势评估值F≥0.92, 几乎达到最优攻击态势; 未考虑RCS影响的导引方式评估值在F=0.7左右, 并未能处于最适合导弹发射的态势。

图 13~14分别显示了2种方法在远距接敌导引过程中雷达探测概率和目标RCS的变化情况, 随着时间的推进, 战机-目标间的距离逐渐缩小, 2种导引方法对应的雷达探测整体都在增大。然而, 由于空战中目标的RCS随雷达入射角动态起伏, 探测概率会随之突变。图 14中, 不考虑RCS约束的远距接敌导引对应RCS跳动频繁且上下落差极大, 由于导引的终点处于目标尾后, 目标动态RCS整体没有增高的趋势; 考虑动态RCS约束的远距接敌导引可以有效减小RCS的剧烈起伏, 且由于最佳占位点选取在目标侧方, 目标的动态RCS随时间整体逐渐增大。反映到图 13, 不考虑RCS约束的远距接敌导引其探测概率会因为RCS的起伏而跳动; 而考虑动态RCS约束的远距接敌导引的探测概率逐步增大, 在到达Pdr=1后基本保持不变, 可以稳定探测目标。

综上所述, 本文使用的考虑目标RCS约束, 基于粒子群进行过载寻优的远距接敌导引法可以导引我方战机朝着目标RCS较大的最佳占位点飞行, 有效减小了目标RCS的起伏程度, 避免RCS陷入数值过小的区间内, 大大降低了远距离跟踪过程中目标丢失的概率, 能更好地为后续导弹制导做准备。

表2

远距接敌导引仿真参数

表3

远距接敌导引场景参数

thumbnail 图9

目标匀速直线的远距接敌导引
thumbnail 图10

目标匀速盘旋的远距接敌导引
thumbnail 图11

未考虑RCS影响的远距接敌导引
thumbnail 图12

态势评估值对比
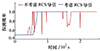thumbnail 图13

瞬时探测概率对比
thumbnail 图14

目标RCS对比

3 结论

随着现代科技尤其是军事科技的快速发展, 空战环境日益复杂, 对载机的导引技术提出了更高的要求。针对超视距条件下载机的导引问题, 本文研究基于RCS约束的远距接敌导引方法。首先, 综合导弹攻击区、目标威胁区和目标全空域RCS的变化特点分析了远距接敌导引的终点目标, 包括最佳攻击占位点和导弹最佳发射态势的研究。其次, 在三维空间内对远距接敌导引中战机-目标相对态势进行建模, 在考虑动态RCS约束条件下从五方面建立了态势的评估函数。再次, 基于态势评估函数, 采用粒子群算法对远距接敌导引中我方战机过载控制量进行寻优, 以此导引我方战机前往最佳占位点完成导弹的发射瞄准。之后, 将考虑RCS的远距接敌导引和未考虑RCS的远距接敌导引进行仿真对比, 结果表明考虑RCS约束的接敌导引在跟踪时目标RCS变化幅度较小, 能避免目标RCS落入数值过小的区间内, 增强了机载雷达探测概率的稳定性, 防止丢失目标。结果表明基于考虑RCS约束的远距接敌导引方法, 可以在一定程度上减小火控攻击中目标丢失的概率, 有效提高战斗机执行火控攻击任务的成功率。

References

  1. SUN Guoxin, WEN Qiuqiu, XU Zhiqiang, et al. Impact time control using biased proportional navigation for missiles with varying velocity[J]. Chinese Journal of Aeronautics, 2020, 33(3): 956–964. [Article] [Google Scholar]
  2. KIM B S, LEE J G, HAN H S. Biased PNG law for impact with angular constraint[J]. IEEE Trans on Aerospace and Electronic Systems, 1998, 34(1): 277–288. [Article] [Google Scholar]
  3. MA Shuai, WANG Xugang, WANG Zhongyuan, et al. BPNG law with arbitrary initial lead angle and terminal impact angle constraint and time-to-go estimation[J]. Acta Armamentarii, 2019, 40(1): 68–78. [Article] (in Chinese) [Google Scholar]
  4. ZHANG Gang, WANG Yunming. The research of guidance model based on the extended proportional guidance law[J]. Fire Control & Command Control, 2016, 41(2): 82–84 (in Chinese) [Google Scholar]
  5. WANG Liguang, YU Changqing, ZHAO Jiong, et al. Improved proportion navigation based on iterative optimization of prediction model[J]. Flight Dynamics, 2021, 39(1): 66–70 (in Chinese) [Google Scholar]
  6. LIU Chang, FAN Shipeng, WANG Jiang, et al. BP neural network-based adaptive biased proportional navigation guidance law[J]. Acta Armamentarii, 2022, 43(11): 2798–2809 (in Chinese) [Google Scholar]
  7. SUN J, LIU C, YE Q. Robust differential game guidance laws design for uncertain interceptor-target engagement via adaptive dynamic programming[J]. International Journal of Control, 2017, 90(5): 990–1004. [Article] [Google Scholar]
  8. SUN Lei, FU Bing, WAN Shizheng, et al. Differential game guidance law based on adaptive dynamicprogramming for the interception of hypersonie targets[J]. Advances in Aeronautical Science and Engineering, 2020, 11(6): 796–802 (in Chinese) [Google Scholar]
  9. HUA Wenhua, ZHANG Yongjun, ZHANG Jinpeng, et al. Differential game guidance law for double missiles with cooperative intercept angle[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 838–844 (in Chinese) [Google Scholar]
  10. YU Jianglong, DONG Xiwang, LI Qingdong, et al. Cooperative differential game guidance method for intercepting maneuvering target[J]. Journal of Command and Control, 2020, 6(3): 217–222 (in Chinese) [Google Scholar]
  11. GUELMAN M, SHINAR J. Optimal guidance law in the plane[J]. Journal of Guidance, Control and Dynamics, 1984, 7(4): 471–476 [Google Scholar]
  12. SUN Jingliang, LIU Chunsheng. An overview on the adaptive dynamic programming based missile guidance law[J]. Acta Automatica Sinica, 2017, 43(7): 1101–1113 (in Chinese) [Google Scholar]
  13. AAMIR M. Nonlinear receding horizon sub-optimal guidance law for the minimum interception time problem[J]. Control Engineering Practice, 2001, 9(1): 107–116 [Google Scholar]
  14. VINCENT T L, MORGAN R W. Guidance against maneuvering targets using Lyapunov optimizing feedback control[C]//Proceedings of the American Control Conference, Anchorage, 2002: 215–220 [Google Scholar]
  15. MOON J, KIM K, KIM Y. Design of missile guidance law via variable structure control[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(4): 659–664 [Google Scholar]
  16. ZHANG Yanxia, ZHANG An, WANG Qiang. Research on unmanned aircraft controlled and autonomous attack system based on fuzzy control theory[J]. Fire Control & Command Control, 2015, 40(12): 44–47 (in Chinese) [Google Scholar]
  17. XIONG Huajie, YU Baoguo, HE Chenglong. UAV path planning method based on lmproved PSO[J]. Computer Measurement & Control, 2015, 40(12): 44–47 (in Chinese) [Google Scholar]
  18. ZHAO Qinglu, ZHOU Chengping. Research on collaborative path planning algorithm based on genetic algorithm[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(1): 46–50 (in Chinese) [Google Scholar]
  19. ZHANG Kun, LI Ke, SHI Haotian, et al. Autonomous guidance maneuver control and decision-making algorithm based on deep reinforcement learning UAV route[J]. Systems Engineering and Electronics, 2020, 42(7): 1567–1574 (in Chinese) [Google Scholar]
  20. ZHANG J, YU Y, ZHENG L, et al. Situational continuity-based air combat autonomous maneuvering decision-making[J]. Defence Technology, 2023, 29: 66–79 [Google Scholar]
  21. HE Xu, JING Xiaoning, FENG Chao. Air combat maneuver decision based on MCTS method[J]. Journal of Air Force Engineering University, 2017, 18(5): 36–41 (in Chinese) [Google Scholar]
  22. XIE Jianfeng, YANG Qiming, DAI Shuling, et al. Air combat maneuver decision based on reinforcement genetic algorithm[J]. Journal of Northwestern Polytechnical University, 2020, 38(6): 1330–1338. [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
  23. QIAN Haili. A path planning method based on dynamic RCS[J]. Electronic Technology & Software Engineering, 2020(6): 75–76 (in Chinese) [Google Scholar]
  24. FANG Wei, FANG Jun, XU Tao, et al. Method of situation assessment in beyond visual range air combat simulation[J]. Computer Simulation, 2019, 36(10): 29–33 (in Chinese) [Google Scholar]
  25. WU Wenhai, ZHOU Siyu, GAO Li, et al. Improvements of situation assessment for beyond visual range air combat based on missile launching envelope analysis[J]. Systems Engineering and Electronics, 2011, 33(12): 2679–2685 (in Chinese) [Google Scholar]
  26. SHIN J J, BANG H. UAV path planning under dynamic threats using an improved PSO algorithm[J]. International Journal of Aerospace Engineering, 2020, 2020(1): 8820284 [Google Scholar]

All Tables

表1

粒子优化算法仿真参数

In the text
表2

远距接敌导引仿真参数

In the text
表3

远距接敌导引场景参数

In the text

All Figures

thumbnail 图1

最优攻击态势分析图
In the text
thumbnail 图2

占位点-水平急转弯
In the text
thumbnail 图3

占位点-置尾机动
In the text
thumbnail 图4

远距接敌导引态势
In the text
thumbnail 图5

相对角度关系示意图
In the text
thumbnail 图6

粒子群算法流程图
In the text
thumbnail 图7

粒子群算法适应度曲线
In the text
thumbnail 图8

过载寻优运行时间
In the text
thumbnail 图9

目标匀速直线的远距接敌导引
In the text
thumbnail 图10

目标匀速盘旋的远距接敌导引
In the text
thumbnail 图11

未考虑RCS影响的远距接敌导引
In the text
thumbnail 图12

态势评估值对比
In the text
thumbnail 图13

瞬时探测概率对比
In the text
thumbnail 图14

目标RCS对比
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.