EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 368-380 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 368 - 380
DOI https://doi.org/10.1051/jnwpu/20254320368
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

无人机集群(UAVs)是战场上侦察态势、攻击重点高敏目标、进行毁伤评估的有力支撑。美国国防部(DoD)[1]提出无人机集群能力是近远期发展的关键技术之一，并认为这种能力可以使美军在无人系统作战中处于优势地位。当下，国内外对无人机集群技术的研究越来越多，主要集中在体系架构[2]、路径规划[3]、任务分配[4]、态势感知[5]、通信组网[2, 6–7]、编队飞行控制[4, 6]、防碰撞技术[8–12]等方面，但对其如何通过作战试验来验证面向使命任务的作战效能还缺乏可借鉴的经验。为推动无人机集群实战化应用，势必要推动其作战试验的相关研究。

装备体系作战试验是检验作战效能和适用性[1]的关键环节。由于装备体系具有涌现性[13]，作战试验变得更为复杂，具有挑战性。无人机集群作战试验是装备体系作战试验的一种，评估时需充分考虑到无人机集群作战试验与无人机平台(单机)作战试验的检验目的不同，避免简单加和单机效能。实际操作中，应结合内外场试验，采用综合性指标，全面展现体系作战任务完成能力。无人机集群任务可靠性可以反映集群在特定时间范围内和特定条件下完成规定任务的能力，是一个较为合理的综合性指标。对任务可靠性的预测是辅助指挥人员进行作战决策的重要依据[14]，据此调整任务规划，可实现对无人机集群作战试验的合理设计。然而目前对无人机集群的任务可靠性特别是单阶段任务可靠性的研究较少，考虑到无人机集群任务可靠性在智能化战争中的重要价值[15]，需深入挖掘其求解方法。

本文提出一种基于任务可靠性的无人机集群作战试验方案的规划方法，为试验规划供参考。

1 国内外研究现状

在体系作战试验的评估目的中，作战效能是当前研究的重点。为了提出更为有效的任务可靠性模型从而支持无人机集群作战试验方案设计，本文首先对现有研究中关于无人机作战效能、无人机集群作战效能以及无人机集群任务可靠性进行梳理，为研究提供支撑。

1.1 无人机作战效能研究现状

无人机系统可完成战术侦察、预警、电子对抗、对地打击等多种任务[2]。

针对无人机作战效能，大量文献对无人机的单阶段(作战领域阶段)作战进行效能评估，研究多集中于指标体系构建和仿真检验结果。初欣阳等[16]构建了基于改进ADC模型的作战效能评估指标体系，在传统ADC模型中引入战场环境影响参数、战术运用系数以及作战保障能力系数，充分考虑了侦察无人机分系统繁多、串并联关系复杂等特点；何媛等[17]提出一种基于粗糙集和神经网络的无人机侦察效能评估方法，构建了效能评估指标体系，然后利用粗糙集理论去除当中的冗余因素，使用遗传优化的BP神经网络构建无人机侦察效能评估模型，仿真结果具备良好的精度；王晓红等[18]采用层次分析法及专家打分法构建侦察无人机生存能力指标体系，结合灰色理论对侦察无人机生存能力进行综合定量评价。然而，构建指标体系的方法无法充分考虑敌我双方对抗情况，且不能很好地将无人机执行任务时影响任务成功与否的动态因素考虑在内。陈思圯[19]分析了察打一体无人机对时敏目标打击的任务过程，构建精度仿真模型分析挂载不同武器对时敏目标攻击的火力精度，构建三维视景仿真模型对时敏目标打击过程进行验证，然而此方法仅考虑了单机与敌方在火力方面的对抗，没有考虑集群视角对抗，以及侦察时敌方干扰带来的影响。

也有一些学者研究了无人机多阶段任务的任务可靠性。Remenyte-Prescott等[20]将无人机作战任务分为起飞、巡航和着陆3个阶段，使用BDD组合方法求解；Steurer等[21]将无人机作战任务分为起飞、飞往着陆区、搜索着陆点以及着陆4个阶段，集成了系统建模语言(SysML)、对偶图误差传播模型(DEPM)和离散马尔可夫链(DTMC)的可靠性分析方法进行分析；Goncalves等[22]将无人机作战任务分为起飞、爬升、途中、搜索和扫描区域、下降和着陆6个阶段，使用故障树和BDDS方法求解；胡杰等[23]将无人机蜂群作战任务分为滑行、起飞、爬升、途中、进场和着陆6个阶段，使用Petri网模型进行求解。上述方法首先划分无人机集群执行任务的阶段，然后计算任务可靠性，但是对于各阶段特别是作战阶段无人机与敌方对抗细节研究较少，在计算任务可靠性时只考虑了无人机的性能可靠性，未考虑无人机与敌方对抗对任务可靠性产生的影响。

1.2 无人机集群作战效能研究现状

目前评估无人机集群作战效能的方法有3种。

第一种是构建作战效能指标体系，往往会融合仿真方法进行验证。陈亮[24]提出了考虑保障度和突防因素、适合于体系作战条件下侦察无人机作战效能改进ADC模型，给出效能指标体系，并使用灰色关联分析法进行求解；王坦等[25]以OODA环路为基础，从感知能力、决策能力、行为能力、安全能力和通信能力五方面建立了有人机/无人机协同作战指标体系，利用可拓层次分析法(EAHP)和模糊评判法得到评价数据，将其作为离散型Hopfield神经网络(DHNN)的参考标准，依据DHNN的联想记忆功能设计了有人机/无人机协同作战效能评估模型，并进行仿真验证；赵蕊蕊等[26]结合不同无人集群关键技术研究中涉及的评价指标，提出了面向无人集群关键技术能力的评估指标设计思路。使用指标体系评估无人机集群能力，虽然有利于细分能力评估，但是无人机集群提供的能力提升远胜多架无人机能力加权[13]，即集群的能力涌现性[27]，此方法对涌现性特点的评估较弱。

第二种是利用仿真平台进行作战模拟，对效能的评估基于分析直观的作战模拟结果(如红蓝方损失率和存活率)进行分析。如：王晓悦等[28]通过开发任务级仿真平台构设了无人蜂群体系典型作战场景，在平台中建立了环境要素模型和实体模型，开展了全流程仿真推演，并依托蒙特卡洛收敛结果数据，获取了蜂群体系对抗结果。仿真模型结果虽然直观，但不能充分利用“作战试验过程”中的数据，还需结合实际操作结果进行验证和调整，从而获得更全面的理解并从中汲取改进经验。

第三种是通过综合指标进行评估，例如，对无人机集群任务可靠性的评估以及最近几年发展出的对无人机集群任务韧性[29]的研究。对无人机集群任务可靠性的研究详见1.3小节。

1.3 无人机集群任务可靠性研究现状

针对无人机系统的特性和复杂性，对无人机系统的可靠性建模主要分为3种类型，包括k-out-of-n模型及其变体、基于故障模式识别和分析的方法(FMEA)及变体、多阶段任务模型(PMS)[30]。其中，多阶段任务模型充分考虑了无人机系统在执行任务时的特性，可以对整个作战活动的可靠性进行评估。Feng等[31]构建了无人机集群的多阶段任务k-out-of-n系统模型，使用基于二元决策图(BDD)的方法分析单个无人机的可靠性；Yin等[32]将执行灾难救援任务的无人机集群建模为线性k-out-of-n、且有动态k, n和共享无人机的F系统，用于监视、定位和货物交付等不同子任务，采用MCEM方法进行可靠性分析；李博[33]将序贯表决模型和PMS可靠性建模结合，提出了一维和二维序贯表决和多阶段任务综合模型及其优化模型；Prescott等[34]采用BDD法研究了多平台多阶段任务的无人机可靠性建模问题；Yang等[35]利用Petri网模型模拟多平台多阶段任务的可靠性。上述方法考虑到不同阶段无人机集群执行任务的差异，但是同样较少考虑各阶段特别是作战阶段无人机与敌方对抗细节，即在计算任务可靠性时只考虑了无人机的性能可靠性，缺少对无人机与敌方对抗对任务成功影响的考量。

因此，本文以无人机集群作战试验中的实际需求为出发点，以构建方案设计模型为目标，以构建无人机集群任务可靠性模型为着力点，对无人机集群作战试验方案设计展开研究。本文所述方案设计思路为作战试验方案设计提供了新视角，且在构建任务可靠性模型时，考虑因素更加全面，建模中充分考虑无人机飞行高度、无人机类型、与敌方对抗和作战环境等因素影响。

2 无人机集群任务可靠性建模

无人机集群可以执行的任务类型[36]中侦察、打击和侦察打击最为常见。本节对3种任务的任务可靠性分别建模，作为试验方案设计时的筛选依据。

2.1 模型假设

本文主要假设有：

1) 侦察区域为矩形；

2) 敌方目标位置固定；

3) 所有型号无人侦察机传感器的最大探测夹角相同；

4) 执行某一任务的过程中无人侦察机的侦察高度不变，且相同类型的侦察机侦察高度相同；

5) 不考虑飞行速度对侦察能力的影响，且所有无人侦察机的速度相同；

6) 无人机在飞行中出现的俯仰、偏航和侧滚情况对飞行任务的影响可以忽略不计。

2.2 作战区域参数

在情报侦察前，作战区域的目标大致位置、数量和型号已有预先情报支援，且根据情报和装备库信息可以推断出该作战区域的如下信息：

1) 作战区域面积: A=L×W, L代表长边, W代表短边;

2) 作战区域敌方一个干扰源j的电磁信号干扰可靠性影响系数为kemij, 表示干扰源对侦察无人机任务可靠性的影响程度, 属于敌方干扰系数;

3) 作战区域敌方一个火力单元z的火力攻击可靠性影响系数为kfpz, 表示火力单元对侦察无人机任务可靠性的影响程度, 属于敌方干扰系数;

4) 作战区域敌方干扰源共有b个, 火力单元共有c个, 需要打击的目标有e个。

2.3 无人机参数

本文中，侦察任务是由侦察机组成的无人机子群前往作战区域搜集情报或确定目标；打击任务是在敌方目标清楚定位的情况下，由具有打击功能的无人机，如自杀式无人机，前往作战区域对敌方目标进行火力打击、摧毁敌方目标；侦察打击任务，即包含由侦察机组成的侦察子群和由攻击机组成的攻击子群，执行任务时，侦察子群先前往作战区域执行侦察任务，传回情报后，再由攻击子群执行打击任务。

我方所含侦察无人机和自杀式无人机的相关指标分别如表 1~2所示。

根据表 1~2，可知有：

表1

侦察无人机相关指标一览表

表2

自杀式无人机相关指标一览表

2.4 无人机集群情报侦察可靠性建模

在侦察机执行任务的过程中，飞行可靠性fiI和目标识别能力riI共同影响着最终侦察任务完成可靠性，如图 1所示。飞行可靠性指无人机能否在特定环境、特定高度和速度下稳定飞行；侦察可靠性则指电磁、红外、压力等传感器在特定环境(作战中特别要考虑敌方的对抗)、特定工作强度下能够保证通信联通和精准导航的能力。

假设每个无人机的寿命服从指数分布, 则第i种侦察机的飞行可靠性函数为

式中，t为侦察机在侦察区域停留的时间, 不同侦察方式的侦察时长不同。

将未遭遇到敌方电磁信号干扰和火力攻击时侦察机的侦察可靠性定义为该侦察机的单机基本任务可靠性, 则定义第i种侦察机的单机基本任务可靠性为ri0I, i=1, 2, …, a1。

划分侦察区域将提高侦察效率, 令单机传感器的探测夹角为α、侦察高度为h, 则单机最大侦察宽度为2htanα, 为保证覆盖所有侦察区域, 区域划分个数 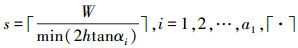表示向上取整，若有侦察区域交叠(当s不能被2整除时), 相互有交叠的3个区域分别为 。

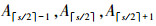在情报侦察阶段，为充分了解敌方情况，假设无人机集群采取单向单次遍飞的地毯式搜索方式。

为了合理分配无人机种类和数量，需确定各子区域敌方威胁的情况，针对无人机的威胁主要有电磁干扰和火力打击2种。由前期情报可得各区域大致敌方干扰源的分布，据此可以计算敌方干扰系数。

根据文献[37]中的经验公式可推测，我方无人机承受的干扰强度与干扰源电磁功率强度呈正比，与无人机和干扰源之间距离(飞行高度)的平方呈反比，如(4)式所示。

式中：PR表示我方无人机接收到的电磁功率；PS表示敌方电磁功率发射强度。

干扰源采用电磁功率的大小与距离我方无人机的远近有关，无人机飞行高度越高，敌方地面干扰源采用的电磁功率越大，且敌方电磁干扰对我方的影响与我方承受的干扰强度呈正比，所以有

故给出作战区域敌方一个干扰源j的电磁信号干扰影响系数定义如(6)式所示。

式中：kj是干扰源系数，与干扰源信号的发射功率、发射波等有关，取值区间为(1, +∞)；τj为抗干扰性能系数，取值区间为(0, 1)，无人机系统通信配置越高，取值越小，即敌方干扰对侦察无人机可靠性的影响越小；Ps表示敌方干扰源发射电磁波的功率。当无人机低空飞行时，通常界限为300 m，由于受到地表复杂环境的掩护，其受电磁信号干扰的可能性大大下降，故取电磁信号干扰的可靠性影响系数为0.01；当地面目标不具备干扰能力时，电磁信号干扰影响系数为0。

那么，1个干扰源下单架侦察无人机的抗干扰能力和子区域Ax上单架侦察无人机的抗干扰能力可由(7)~(8)式得出。

式中：bx表示子区域Ax包含的敌方干扰源个数。

由于不同类型侦察无人机的抗火力打击能力区别不大, 计算侦察无人机抗打击能力时仅考虑目标的差异。对于作战区域敌方的一个火力单元z, 其火力攻击影响系数为

式中: W表示敌方武器集合; w1表示单兵防空导弹；w2表示防空炮。无人机在敌方武器火力攻击范围内基本难以逃脱，故考虑攻击无人机费效比合理的敌方目标，比如单兵防空导弹、防空炮，一般对无人机的毁伤概率很高，将导致无人机的任务可靠性降低一半；其他情况下，比如对于没有攻击能力的或者攻击无人机费效比过高的敌方目标，火力攻击可靠性影响系数为0。

同理，一个火力单元下单架侦察无人机的抗打击能力和子区域Ax上单架侦察无人机的抗打击能力可由(10)~(11)式得出。

式中, cx表示子区域Ax的敌方火力单元个数。

且有, 单架侦察无人机在子区域Ax上费用损耗如(12) 式所示。

式中：Ca表示第a型号侦察无人机的造价。

子区域Ax上发生的费用损耗如(13) 式所示。

式中：nixI表示第i型号侦察无人机在第x个子区域上分配的数量。

因此, 某一子区域上飞行高度为h的第i种侦察机的实际侦察任务可靠性riI计算方法如(14)式所示。

特别地, 当某个子区域不派无人机时, 该区域的任务可靠性也视为1。

则可用(15)式计算第x个子侦察区域上的侦察可靠性。

式中：fiI为第i种侦察机的飞行可靠性；lxi为第x个侦察区域上分配的第i种无人机数量；t为侦察机经历1次某子侦察区域的时间。

最后, 综合考虑各子区域上的侦察可靠性，以及在任务执行过程中整个侦察无人机集群的抗干扰能力, 整个侦察无人机集群在整个作战领域上的侦察可靠性计算如(16)式所示。

式中, RACI表示无人机集群执行侦察任务过程中的抗干扰能力, 工程应用上通信设备在规定的使用范围内可以保障通信和导航, 各通信设备构成冷备结构, 通常无人机的通信源备份只有1个, 可靠性框图如图 2所示。因此, 无人机集群执行侦察任务通信源可靠性的计算如(17)式所示[4]。

式中：β为通道出现故障的概率(假设不同通道单位时间出现故障的次数相同)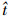；为通信链路工作的时间，在本文中即为在作战区域上空完成侦察任务花费的时间; ζ为开关K的可靠性(即某一个通信源故障后及时切换到另一个通信源的可靠性)。

不考虑通信设备的成本, 算出整个作战任务的费用损耗如(18)式所示。

thumbnail 图1

侦察任务可靠性组成
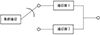thumbnail 图2

无人机集群通信源备份情况可靠性框图

2.5 无人机集群打击任务可靠性建模

本文的攻击型无人机指自杀式无人机, 其打击任务可靠性包含飞行可靠性、目标识别能力和目标打击能力, 如图 3所示。

飞行可靠性和目标识别可靠性的计算同侦察无人机, 目标打击可靠性的计算与打击距离、作战环境、无人机挂载等有关[38], 因此第i种自杀式无人机的目标打击能力如(19)式所示。

式中：kD为距离系数, 与自杀式无人机距敌方目标的直线距离有关[39], 如(20)式所示; kE为环境影响系数, 取值如表 3所示, 反映能见度、风力等[40–42]作战环境对自杀式无人机打击效果的影响; pDAM为毁伤概率[43–44], 即自杀式无人机击中目标后摧毁目标的可能性, 计算方法如(21) 式所示。

式中：d为自杀式无人机发出位置和目标位置间的直线距离, 在无人机集群执行打击任务之前即可明确, 特别地, 为了简化计算, 忽略自杀式无人机处于不同飞行高度时d的差异; RiA为第i种自杀式无人机的毁伤半径(即开始对敌发动自杀式打击最大距离); Rj为第j种敌方目标的攻击半径(当敌方目标不具备攻击能力时, 取0);RiAI为第i种自杀式无人机的侦察半径。

式中：RCEPi表示第i种自杀式无人机打击圆公算偏差, 反映了自杀式无人机的命中精度[11]，该值越大, 打击精度越差。

由(20)式可知, 鉴于敌方各目标位置不同, 某型号单架自杀式无人机的打击任务可靠性需要针对敌方目标逐一计算。(22)式表示飞行高度为h的单架第i种自杀式无人机针对g个目标的实际打击可靠性。

式中：Rantiemi, x表示子区域Ax上单架自杀式无人机的抗干扰能力；Rantifp, x表示子区域Ax上单架自杀式无人机的抗打击能力, 计算方法同侦察机; ri0AI为第i种自杀式无人机的单机基本任务可靠性; fiA为第i种侦自杀式无人机的飞行可靠性; t为自杀式无人机从发出位置到敌方目标位置经历的时间。由(22)式可以看出, 针对相同类型敌方武器, 所处的子区域不同会导致计算得出单架自杀式无人机的任务可靠性不同, 这是因为不同子区域上敌方对我方无人机整体干扰情况会有所区别。

特别地, 为了完成打击任务, 包含敌方目标的子区域必须分配自杀式无人机。

针对第g个目标, 自杀式无人机集群的目标打击可靠性如(23)式所示。

式中, lgi为针对第g个敌方目标第i种自杀式无人机被分配的数量。

接着, 用(24) 式可计算出整个自杀无人机集群在全作战领域上的目标打击可靠性。

式中, RACA表示无人机集群执行任务过程中的集群抗干扰能力, 计算方法与无人机集群执行侦察任务的集群抗干扰能力类似, 参考(17)式。

不考虑通信设备的成本和自杀式无人机的收回, 整个作战任务的费用损耗如(25) 式所示。

thumbnail 图3

打击任务可靠性组成
表3

无人机作战环境影响系数取值表

2.6 无人机集群侦察打击任务可靠性建模

无人机集群执行先侦察后打击任务时, 侦察任务和打击任务属于串联关系, 此时任务可靠性计算如(26)式所示, 作战总成本由(27)式计算得出。

式中：RAM表示作战区域A上无人机集群任务可靠性。

3 无人机集群作战试验方案设计

3.1 作战试验方案设计建模

以无人机集群侦察打击任务为例, 进行试验方案设计时, 方案计算得出的RMA需要不低于作战要求的任务可靠性下界 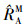, 并且要对成本进行控制, 因此可以给出试验方案设计模型，如(28) 式所示。

3.2 多目标量子粒子群算法

本文所述模型属于多目标整数优化问题。针对多维输入的整数优化问题，可以采用粒子群算法(particle swarm optimization, PSO)或其变体。传统的PSO方法需要预先设定的参数过多，不利于找到待优化模型的最优参数，且粒子位置变化缺少随机性，容易陷入局部最优的陷阱[45]。因此采用量子粒子群(quantum particle swarm optimization, QPSO)算法进行求解。QPSO算法取消了粒子的移动方向属性，粒子位置的更新不再与粒子之前的运动相关，这样就增加了粒子位置的随机性[46]。进一步地，可以对粒子位置进行整数规格化，达到解决整数优化问题的目的。针对多目标优化问题，由于各个目标之间相互制约，可能一个目标性能的改善是以损失其他目标性能为代价的，不可能存在一个使所有目标性能都达到最优的解，所以对于多目标优化问题，其解通常是一个非劣解的集合——帕累托(Pareto)解集，因此要使用多目标优化算法求解，多目标粒子群(multi-objective particle swarm optimization algorithm, MOPSO)算法将原本只能用在单目标上的PSO应用于多目标上。综上，本文拟采用多目标量子粒子群算法(multi-objective quantum particle swarm optimization algorithm, MOQPSO)进行求解。

3.3 计算流程及步骤标量子粒子群算法

QPSO相对于PSO, 改进了pbest的计算方法; MOQPSO则进一步根据多目标问题改进了gbest的选取方法, 因此在PSO的求解步骤基础上进行改进, 得到MOQPSO的求解步骤如下。

步骤1  随机初始化粒子群坐标以及一些基本参数, 比如种群大小、存档大小、迭代次数、权重系数等;

步骤2  计算适应值, 将每个粒子当前的适应值作为自身初始pbest;

步骤3  根据Pareto支配原则, 计算得到Archive集(存放当前的非劣解);

步骤4  计算Archive集中的拥挤度, 据此得到初始gbest;

步骤5  更新粒子群位置;

步骤6  计算适应值并更新粒子群pbest(支配法: 无法判别优劣的情况下随机选择的方法);

步骤7  根据Pareto支配原则, 更新存档；

步骤8  计算Archive集中的拥挤度, 更新gbest(存档若是超出最大存储粒子数则根据自适应网格法裁剪);

步骤9  收敛或者达到最大迭代次数则退出循环; 否则, 转到步骤4继续循环。

4 实例分析

4.1 作战试验区域设定

情报可知某侦察区域敌方分布如图 4所示, W为16 km, L为20 km。干扰源、火力单元(单兵火箭炮和防空炮)及打击目标等用图标表示。

根据敌方干扰源和火力单元分布情况, 确定不同高度区域划分。据前文分析, 300 m为无人机受电磁信号干扰的临界点, 而实战中无人机集群飞行最高高度为2 000 m左右, 分别选取无人机飞行高度为300, 500, 1 000, 2 000 m。

我方可选侦察无人机的相关指标如表 4所示。我方可选自杀式无人机的相关指标如表 5所示。

按照表 4所示我方可选无人机参数，以侦察范围较小的无人机侦察范围为准，按照前述方法，当飞行高度为300, 500, 1 000, 2 000 m时，可分别将侦察区域划分为16, 10, 5, 4个子区域。特别地，不存在敌方目标的区域任务可靠性为1，故仅考虑包含敌方目标的区域，并以敌方目标的中心确定其所在区域，因此可以简化不同飞行高度下的敌方区域如表 6所示。需要打击的敌方目标基本情况如表 7所示。

thumbnail 图4

作战区域情报图
表4

可选侦察无人机相关指标一览表

表5

我方可选自杀式无人机相关指标一览表

表6

简化后的敌方区域威胁情况

表7

简化后的敌方目标基本情况及在无人机不同飞行高度下所属的区域

4.2 无人机集群侦察打击任务方案设计

在无人机集群执行侦察打击任务之前，是不知道敌方目标的准确位置的。简单推理可知，若目标位置在一个区间内取值时方案无法成为帕累托最优方案，则其在目标位置确定时一定不可能成为帕累最优方案。进一步地，根据仿真结果，还需对比不同方案任务可靠性的稳定性和平均最优情况。

因此针对无人机集群侦察打击任务的实例分析，本文将分2步进行：

1) 使用前述MOQPSO方法，筛选得到较为合理的帕累托最优方案集；

2) 针对集合中的方案，再进行仿真验证，分析不同方案有多大概率是更优的，据此筛选出更为可靠的方案。

4.3 无人机集群侦察打击任务帕累托最优方案

干扰源系数k取1 000，可得各子区域上2种型号侦察无人机和2种型号自杀式无人机的抗干扰能力和抗打击能力分别如表 8~11所示。

令通道出现故障的概率β取0.001, 开关K的可靠性ζ取0.999 99, 使用MOQPSO代码, 设置循环次数为10 000次, 得到的帕累托曲线如图 5所示, 可以看出收敛性良好。挑选前2个最优方案, 相关结果如表 12所示，方案1的总任务可靠性为0.990 5, 总成本为2 170万元，方案2的总任务可靠性为0.990 4，总成本为2 170万元。

表8

型号一侦察机抗干扰和抗打击能力一览表

表9

型号二侦察机抗干扰和抗打击能力一览表

表10

型号一自杀式无人机抗干扰和抗打击能力一览表

表11

型号二自杀式无人机抗干扰和抗打击能力一览表

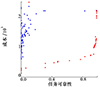thumbnail 图5

多目标量子粒子群算法循环10 000次后的帕累托曲线
表12

无人机集群侦察打击任务帕累托最优方案

4.4 概率更优帕累托最优方案

由于在执行侦察打击任务前敌方目标位置是在一个区间内取值，所以将不同方案进行比较时，还需考虑不同方案任务可靠性的稳定性和平均最优情况，为指挥人员决策提供更加客观的参考。下面对初步筛选方案的置信度进行进一步分析。

假设在最后筛选中，重点考虑可靠性，在表 7所示的距离范围中，分别对每个分配方案进行100次循环，为了更准确地比较2种方案的优劣，分别对其结果中可靠性大于0.98的结果占比(参数Ⅰ)、可靠性均值(参数Ⅱ)和方差(参数Ⅲ)进行统计，2个方案循环100次的数据结果如表 13所示。

由仿真结果可以看出，方案2比方案1可靠性取值更加稳定，且整体更优，因此对比这2个方案，选择方案2，即方案2为最优方案。

表13

2个方案优劣性对比

5 结论

本文在回顾国内外研究基础上，以无人机集群侦察打击任务为例，构建了无人机集群作战区域阶段任务可靠性计算模型，并基于此进行了无人机集群作战试验方案设计。

无人机集群作战试验方案是在预先情报的支持下，在作战试验区域内对特定类型的无人机进行分配。在作战试验方案设计的时候，需要考虑敌方的威胁。对于侦察任务，需着重确保无人机飞行可靠性与目标识别准确性，敌方干扰和火力攻击是主要威胁因素，同时要考虑无人机集群执行侦察任务时的集群抗干扰能力。针对打击任务，需确保自杀式无人机的飞行可靠性与目标识别能力，同时目标打击效果是任务成功的关键，类似地，需要考虑无人机集群执行打击任务时的集群抗干扰能力。针对侦察打击任务，需要考虑到侦察任务和打击任务串联性。进一步地，不同分配方案得到的结果也不同，在比较时，综合考虑可靠性和成本目标得到不同飞行高度下的帕累托方案，然后再与目标任务可靠性进行对比，考虑费用等条件，确定最终的试验方案。

本文方法为无人机集群试验方案设计提供了新视角。篇幅所限，本文研究仅仅是一个起步，在未来的研究中，对无人机集群任务可靠性进行建模时，可以补充考虑无人机之间的通信，以及更多的区域划分方式和无人机集群飞行方式，后续将展开更深入的研究。

References

  1. United States Department of Defense. Unmanned systems integrated roadmap FY2017-2042[EB/OL]. (2018-08-30)[2023-12-18]. [Article] [Google Scholar]
  2. LI Hao, SUN Hemin, LI Hongquan, et al. A review of UAV cluster swarm operations and their early warning detection response strategies[J]. Scuderia Missile, 2018(11): 46–51 (in Chinese) [Google Scholar]
  3. YANG Zhongying, WANG Yulong, LAI Chuanlong. A study of the current status and trends in the development of UAV swarm warfare[J]. Scuderia Missile, 2019(5): 34–38 (in Chinese) [Google Scholar]
  4. YU Yifan, WANG Lei. A study of the current status and trends in the development of UAV swarm warfare[J]. Scuderia Missile, 2019(2): 34–42 (in Chinese) [Google Scholar]
  5. WANG Xiangke, LIU Zhihong, CONG Yirui, et al. Miniature fixed-wing UAV swarms: review and outlook[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(4): 15–40 (in Chinese) [Google Scholar]
  6. JIA Yongnan, TIAN Siying, LI Qing. Recent development of unmanned aerial vehicle swarms[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(suppl. 1): 1–11 (in Chinese) [Google Scholar]
  7. ZHU Wenjin, WANG Luohaoji, CAI Zhiqiang, et al. Resilience analysis for reconfigurable network with cascading failures[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 839–846. [Article] (in Chinese) [Google Scholar]
  8. WAQAS A, KANG D, CHA Y. Deep learning-based obstacle-avoiding autonomous UAVs with fiducial marker-based localization for structural health monitoring[J]. Structural Health Monitoring, 2024, 23(2): 971–990 [Google Scholar]
  9. XU Zhao, HU Jinwen, MA Yunhong, et al. A study on path planning algorithms of UAV collision avoidance[J]. Journal of Northwestern Polytechnical University, 2019, 37(1): 100–106. [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
  10. ZHANG Qiqian, XU Weiwei, ZHANG Honghai, et al. The obstacle-avoidance path planning for UAV based on IOCAD[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 238–245. [Article] (in Chinese) [Google Scholar]
  11. ZHANG Qianyu, LI Qingqing, SUN Ruijie. Construction of operational-effectiveness-test indicators for aircraft carrier anti-ship equipment system-of-system[J]. Journal of Ordnance Equipment Engineering, 2019, 40(12): 1–4 (in Chinese) [Google Scholar]
  12. GUO Xinwen, ZHANG Zhengjuan. The study of organization model of operational range test for long range ballistic aircraft[J]. Journal of Northwestern Polytechnical University, 2019, 37(1): 44–49 (in Chinese) [Google Scholar]
  13. HE Qiang, WANG Ying. SoS and systems in engineering practice[J]. Science & Technology Review, 2018(20): 32–37 (in Chinese) [Google Scholar]
  14. ANDREWS J D, POOLE J, CHEN W H. Fast mission reliability prediction for unmanned aerial vehicles[J]. Reliability Engineering & System Safety, 2013, 120: 3–9 [Google Scholar]
  15. LU Nan, WANG Xiaodong, TANG Zheng, et al. Modeling method of unmanned aerial vehicle swarm behavior based on spatiotemporal hybrid Petri net[J]. Journal of Northwestern Polytechnical University, 2022, 40(4): 812–818. [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. CHU Xinyang, LIAO Xuejun, XU Qinxian, et al. Improved ADC method for operational effectiveness evaluation in operational test of unmanned reconnaissance aircraft[J]. Journal of Ordnance Equipment Engineering, 2020, 41(8): 89–96 (in Chinese) [Google Scholar]
  17. HE Yuan, GAN Xusheng, TU Congliang, et al. UAV reconnaissance effectiveness evaluation based on rough set and neural network[J]. Firepower and Command and Control, 2021, 46(3): 20–25 (in Chinese) [Google Scholar]
  18. WANG Xiaohong, LI Long, WANG Shengchun, et al. Assessment of reconnaissance UAV viability based on GAHP[J]. Military-Industrial Automation, 2022, 41(2): 23–27 (in Chinese) [Google Scholar]
  19. CHEN Siyi. Design and simulation realization of hitting process of reconnaissance and combat integrated drones on time-sensitive targets[D]. Chengdu: University of Electronic Science and Technology of China, 2019 (in Chinese) [Google Scholar]
  20. REMENYTE-PRESCOTT R, ANDREWS J D, CHUNG P W H. An efficient phased mission reliability analysis for autonomous vehicles[J]. Reliability Engineering & System Safety, 2010, 95(3): 226–235 [Google Scholar]
  21. STEURER M, MOROZOV A, JANSCHEK K, et al. Model-based dependability assessment of phased-mission unmanned aerial vehicles[J]. IFAC-PapersOnLine, 2020, 53(2): 8915–8922 [Google Scholar]
  22. GONCALVES P, SOBRAL J, FERREIRA L A. Unmanned aerial vehicle safety assessment modelling through Petri nets[J]. Reliability Engineering & System Safety, 2017, 167: 383–393 [Google Scholar]
  23. HU Jie, CHEN Hualiang, LIU Liang, et al. Research on operational effectiveness evaluation of UAV swarm[J]. Fire Control & Command Control, 2022, 47(4): 164–168 (in Chinese) [Google Scholar]
  24. CHEN Liang. UAV operational effectiveness evaluation model in system combat[J]. Naval Electronics Engineering, 2016, 36(7): 124–127 (in Chinese) [Google Scholar]
  25. WANG Tan, YANG Sen, QI Xiaohui, et al. Effectiveness evaluation of MAV/UAV cooperative operations based on hopfield neural network[J]. Electro-Optics and Control, 2021, 28(10): 80–84 (in Chinese) [Google Scholar]
  26. ZHAO Ruirui, YU Haiyue, YOU Yaqian, et al. Review on current status and technology method of unmanned swarm test evaluation[J]. Systems Engineering and Electronics, 2024, 46(2): 570–585 (in Chinese) [Google Scholar]
  27. HU Xiaofeng, ZHANG Bin. SoS complexity and SoS engineering[J]. Journal of Chinese Academy of Electronic Science, 2011, 6(5): 446–450 (in Chinese) [Google Scholar]
  28. WANG Xiaoyue, WANG Xun, WANG Yongzhen, et al. Evaluation method for combat effectiveness of task-based simulated UAV swarm system[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(suppl. 1): 726937 (in Chinese) [Google Scholar]
  29. CHENG Congcong. Mission-oriented UAV cluster toughness assessment research[D]. Changsha: National University of Defense Technology, 2020 (in Chinese) [Google Scholar]
  30. XING L, JOHNSON B W. Reliability theory and practice for unmanned aerial vehicles[J]. IEEE Internet of Things Journal, 2023, 10(4): 3548–3566 [Google Scholar]
  31. FENG Q, LIU M, DUI H, et al. Importance measure-based phased mission reliability and UAV number optimization for swarm[J]. Reliability Engineering & System Safety, 2022, 223: 108478 [Google Scholar]
  32. YIN J, CUI L, SUN Y, et al. Reliability modelling for linear and circular k-out-of-n: F systems with shared components[J]. Reliability Engineering & System Safety, 2022, 219: 108172 [Google Scholar]
  33. LI Bo. Study on resilience evaluation for the mission-oriented UAV swarm[D]. Changsha: National University of Defense Technology, 2018 (in Chinese) [Google Scholar]
  34. PRESCOTT D R, ANDREWS J D, DOWNES C G. Multiplatform phased mission reliability modelling for mission planning[J]. Journal of Risk and Reliability, 2009, 223(1): 27–39 [Google Scholar]
  35. YANG C, YANG J, DONG P, et al. Reliability model of multiplatform phased mission system based on CPN[C]//2010 IEEE International Conference on Industrial Engineering and Engineering Management, 2010 [Google Scholar]
  36. YANG Lina, CAO Zeyang, LI Yongxiang. Research on the operational structure and concept of unmanned aerial swarm[J]. Modern Defense Technology, 2020, 48(4): 44–51 (in Chinese) [Google Scholar]
  37. JI Yuefeng. Modern communications technology[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2020 (in Chinese) [Google Scholar]
  38. QU Gaomin. Ground attack UAV operational effectiveness assessment and software development[D]. Nanchang: Nanchang Aviation University, 2015 (in Chinese) [Google Scholar]
  39. ZHANG Xuemei. Operational effectiveness evaluation of ground attack UCAV[D]. Xi'an: Northwestern Polytechnical University, 2007 (in Chinese) [Google Scholar]
  40. 翼达蔚蓝 影响无人机飞行的因素(无人机飞行六大气象环境) [EB/OL]. (2023-03-03)[2023-12-18]. [Article] [Google Scholar]
  41. 舟山海事 能见度不良时, 切莫"雾"入歧途! (2023-03-01)[2023-12-18]. [Article] [Google Scholar]
  42. Standardization Administration of China General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Meteorological standards[S]. GB/T 28591-2012, 2012 [Google Scholar]
  43. YUE Yuan, DONG Yanfei, XU Guanhua, et al. Task oriented for cooperation of manned/unmanned fighters in air-to-ground attacking probability model[J]. Firepower and Command and Control, 2015, 40(2): 53–57 (in Chinese) [Google Scholar]
  44. YUE Yuan. The research of UCAV combat simulation modeling[D]. Nanchang: Nanchang Aviation University, 2015 (in Chinese) [Google Scholar]
  45. Nico Phymat 【超参数寻优】量子粒子群算法(QPSO)超参数寻优的python实现 [Article] [Google Scholar]
  46. Ai工匠 多目标优化问题的算法及其求解 (2018-09-06)[2023-12-28]. [Article] [Google Scholar]

All Tables

表1

侦察无人机相关指标一览表

In the text
表2

自杀式无人机相关指标一览表

In the text
表3

无人机作战环境影响系数取值表

In the text
表4

可选侦察无人机相关指标一览表

In the text
表5

我方可选自杀式无人机相关指标一览表

In the text
表6

简化后的敌方区域威胁情况

In the text
表7

简化后的敌方目标基本情况及在无人机不同飞行高度下所属的区域

In the text
表8

型号一侦察机抗干扰和抗打击能力一览表

In the text
表9

型号二侦察机抗干扰和抗打击能力一览表

In the text
表10

型号一自杀式无人机抗干扰和抗打击能力一览表

In the text
表11

型号二自杀式无人机抗干扰和抗打击能力一览表

In the text
表12

无人机集群侦察打击任务帕累托最优方案

In the text
表13

2个方案优劣性对比

In the text

All Figures

thumbnail 图1

侦察任务可靠性组成
In the text
thumbnail 图2

无人机集群通信源备份情况可靠性框图
In the text
thumbnail 图3

打击任务可靠性组成
In the text
thumbnail 图4

作战区域情报图
In the text
thumbnail 图5

多目标量子粒子群算法循环10 000次后的帕累托曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.