EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 496-508 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 496 - 508
DOI https://doi.org/10.1051/jnwpu/20254330496
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

无人水下航行器(unmanned underwater vehicle, UUV)的高精度自定位在导航、监视、海底测绘、水下搜救等诸多领域中具有至关重要的作用。通常, UUV利用航位推算系统或惯性导航系统进行定位导航, 具有自主、隐蔽、实时、不易受外界环境干扰等优点, 然而这些方法的导航定位误差会随着时间不断累积增加, UUV长时间远航程航行时就会产生大的位置累积误差, 不能保证任务的准确执行。因此, 在UUV长时间的航行中, 要通过其他方法对UUV的位置进行校正[1-4]。一种方法是通过全球定位系统(global positioning systems, GPS)或北斗卫星导航系统(BeiDou navigation satellite system, BDS)进行位置校正。但是GPS和BDS的电磁波信号在水下衰减严重, 只能传播几米的距离, UUV必须上浮至水面附近才能接收到GPS或BDS信号, 这种操作尤其在深海情况下是非常耗能费时的, 且容易被发现, 影响其隐蔽性。另一种方法是利用水声定位系统对UUV进行定位, 例如水声传感器网络(underwater acoustic sensor networks, UASN)对UUV位置进行校正。

UASN是由具有声学通信与计算能力的传感器节点构成的水下监测网络系统, 节点间通过水声信号进行无线通信组网。UASN的目标定位可通过各种不同的测量值和不同的定位方法实现。常见的测量物理量可分为以下几类: 到达时间(time of arrival, TOA)、到达时间差(time difference of arrival, TDOA)、接收信号强度(received signal strength, RSS)、到达角度(angle of arrival, AOA)、多普勒频率类测量或者这几种不同物理量组合[5-7]。TOA和TDOA属于时间测量值, 利用时间测量值进行高精度定位是目前最常用的定位方式, 但基于TOA或TDOA测量的方法都要求UASN节点之间具有精确的时钟同步。水下环境复杂, 如声速不均匀、传播时延长、节点易漂移、通信耗能高等, 这些都使水下节点间、节点与UUV间很难做到精确的时钟同步, 且维持时钟同步的成本很高[8]。

由于海洋中介质的非均匀性, 以及声速是压力、温度和盐度的函数而导致声速分布不均匀, 使得声波在海洋传播过程中其声线发生了弯曲[9-11]。对于基于TOA或TDOA测量来定位的UASN, 用平均声速乘以TOA或者TDOA来计算声线传播的直线距离或者距离差, 可满足一定的定位精度要求, 但如果平均声速选取不准确, 会进一步引起更大的定位误差[12-13]。为了保证UUV较高的定位精度, 必须进行声线修正。国内外对声线弯曲修正进行了研究, 常用的方法包括有效声速法、根据射线声学原理进行计算的迭代法、查表法[14-17]。然而这3种方法都是针对时钟同步网络, 要求UUV、节点间精确的时钟同步。

在深海中, 由于声线类型简单、数量较少且易区分[18], 射线声学原理的迭代法适用于深海UUV的定位。对于异步时钟UASN的深海UUV定位, 节点可配备测向功能装置, 可以测得声线在节点处的掠射角。当节点处掠射角已知时, 根据分层介质的射线声学原理可以求出声线的水平传播距离。

本文针对UASN深海UUV定位中, UUV、节点间时钟异步和声线弯曲问题, 提出了一种基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法。该方法在掠射角测量值已知时可以计算精确的UUV和节点间水平距离, 并在掠射角测量值存在误差情况下通过微分迭代逼近方法提高了UUV的定位精度。此外, 本文仿真了掠射角测量值存在误差情况下基于掠射角声线修正的水平距离估计效果, 对定位时节点深度的设置和通信范围内节点的选择具有实际的指导意义。

1 UUV水声定位测量模型和问题描述

UASN节点分布在海面附近, UUV在深海中航行。定位原理示意图如图 1所示, 图中有M个传感器节点和1个UUV, 传感器节点的真实位置已知, 假设 s i=[xi, yi, zi]T, i=1, 2, …, M, UUV的真实位置 u o=[xo, yo, zo]T未知, 通过UASN对UUV进行定位。UUV发射定位请求信号, 节点i测得信号从UUV到节点i的传播时间TOA值τi, TOA测量值τi可以转化为距离测量值di。

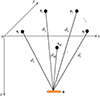thumbnail 图1

UASN目标定位原理示意图

M个节点可获得M个距离测量值, 向量形式的测量模型可以表示为

式中: d o=[d1o, d2o, …, dMo]T是真实的距离向量; n d=[nd1, nd2, …, ndM]T是距离测量噪声向量。

对于上述描述的UUV水声定位问题, 采用最大似然估计算法、最小二乘估计算法或凸优化算法可以估计出UUV的位置 u o。但由于声速空间分布不均匀和声线弯曲, 如果选用平均声速c计算UUV到节点的距离向量 d, 距离测量误差 n d会很大, 导致上述方法估计的UUV位置误差也会很大, 无法满足UUV的高精度定位需求。因此, 要想根本上提高UUV定位精度, 必须先提高节点和UUV间的距离估计精度, 再采用优良的目标定位算法提高UUV的定位精度。

因此为了得到更加精确的UUV位置, 必须采用声线修正方法使距离测量值di更加精确。本文针对深海UUV水声定位中声线弯曲特点和UUV、节点时钟异步情况, 提出了一种基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法, 可以得到更加精确的UUV和节点间水平距离ri, 并针对掠射角测量值存在误差情况, 采用微分迭代逼近的目标定位方法, 使UUV位置估计得更加精确。

2 深海UUV免时钟同步定位方法

2.1 分层介质中的射线声学

在水声中, 射线声学是常用的一种处理问题方法。水中声速分布不均匀, 导致声线传播方向发生弯曲。海水中的声速受温度、盐度、压力的影响, 这3个要素都随深度而变, 且具有垂直分层特性, 因此海水中的声速也随深度而变且具有垂直分层特性。工程上往往在测得随深度z变化的声速分布c(z)后, 沿深度方向将其分成若干层, 并使每层中的相对声速梯度a等于常数, 这就是分层介质模型。

射线声学所遵循的基本规律是Snell定律, 表示为

式中：αi为深度zi(第i层边界)处声线与水平坐标x轴的夹角, 称为掠射角；ci为该深度上的声速；α0, c0为某特定深度上, 如声源深度上声线出射处的掠射角和声速。若α0和声速的垂直分层分布c(z)已知, 则可由Snell定律求出海洋中任意深度处声线的掠射角, 从而确定了任意深度处声波传播方向。

深海UUV水声定位中, UUV位于传感器节点下方, 如图 1所示, UUV发送声信号, 声线从UUV发射出来, 向上弯曲传播到达传感器节点处。图 2为分层介质模型的声速和声线图, 其中图 2a)为声速剖面, 图 2b)为声线轨迹。

thumbnail 图2

分层介质模型的声速和声线图

1

图 2中, r为声线传播的水平距离, 当声速分布近似为多层恒定梯度分布时, 按照声线初始掠射角α0和射线声学原理可以求出各层的水平距离和传播时间。设zi, αi分别代表第i层介质边界处的深度、声线掠射角, 分别代表第i层介质的声速梯度、声线经过第i层的水平距离和传播时间。垂直分层模型条件下, N分层声线的水平距离和传播时间为

式中

从(3)~(6)式可以看出, 声线经过的水平距离和传播时间都是声线初始掠射角α0的函数, 在UUV深度、节点深度和声速剖面(由温深曲线计算得到)已知的情况下, 对于每个初始掠射角α0, 必有一个水平距离和传播时间与它对应。在异步UASN深海UUV定位中, UUV和节点时钟不同步, 在节点测得声线掠射角情况下, 本文提出了一种基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法, 用于提高深海UUV的定位精度。

2.2 基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法

UUV在深度z处向外发射定位请求信号, 声线到达各个节点处。根据声速变化情况, 将声速剖面近似成垂直多层等声速梯度分布。

对于节点 s i, i=1, 2, …, M, UUV深度z0和节点深度zi之间由下到上共有N个等声速梯度层, 可以测得节点处到达掠射角为αN, 由(2)式可得每个分层处的掠射角为

由(3)式和(5)式可求得节点 s i到UUV的水平距离为

M个节点 s i可得到M个节点到UUV的水平距离ri, 则

将实测的各节点处掠射角代入(7)~(9)式, 通过最小二乘算法估计出UUV位置的初值 u 0=[x0, y0]T。

由UUV位置的初值计算出UUV到各个节点的水平距离

令 , 则fi(x, y, xi, yi)在(x, y)处的全微分为

M个fi(x, y, xi, yi)在 u 0=[x0, y0]T处的全微分为

式中, Δri=ri-r′i。令 δ =[Δx, Δy]T, 则(12)式可表示成 Gδ = h, 利用最小二乘估计算法可求得

式中

用修正量 δ对UUV位置的初值进行修正, 使UUV位置的新设定值为

将(x′, y′)作为UUV位置的初值, 重复计算(10)~(15)式, 直到 δ满足迭代结束条件, 则此时(x′, y′)作为UUV最终定位结果, 即 u =[x′, y′]T。

迭代结束条件为

式中, ε为一很小的门限值。

综上所述, 可总结出基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法计算流程。

准备工作: 对实验声速数据或实验区域的实测声速数据, 进行3次样条插值, 得到光滑的声速剖面。

步骤1传感器节点配置垂直线列阵, 如图 3所示, 测得从UUV射出的声线在节点处的掠射角αN;

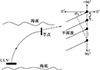thumbnail 图3

节点垂直线列阵测向示意图

步骤2确定节点、UUV的深度, 根据声速变化情况将声速剖面分成N层等声速梯度, 每层分界处的声速值为cj(j=0, 1, 2, …, N);

对于UUV水声定位, 通常UUV上安装了深度传感器测量其深度z, 调制后通过水声信道将其发送给各个节点。

步骤3根据(7)~(8)式, 计算出UUV到各节点的水平距离ri(i=1, 2, …, M);

步骤4采用最小二乘算法计算出UUV位置的初值 u 0=[x0, y0]T;

步骤5根据(10)~(15)式计算出 δ和UUV位置的新设定值(x′, y′);

步骤6判断(16)式迭代结束条件是否满足, 如果不满足, 则重复步骤5, 直到满足结束条件为止, 得到UUV的最终定位结果。

基于时间的传统声线修正方法要求节点和UUV之间时钟同步, 在计算声线传播水平距离时需要进行多次迭代。而本文提出的基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法不要求节点和UUV之间时钟同步, 在计算声线传播水平距离时只进行了1次计算, 所以本文提出的声线修正方法计算复杂度低、运算速度快。

为了提高掠射角测量值存在误差情况下UUV的定位精度, 本文提出的微分迭代的定位方法根据全微分定义构建包含UUV位置修正量 δ的方程组, 采用最小二乘方法求解修正量, 多次迭代求得更加精确的修正量, 进而提高UUV的定位精度。

3 定位方法性能仿真和分析

本文所提方法需要节点测得UUV射出声线在节点处的掠射角αN, 为了验证本文所提方法的可行性和有效性, 本文利用(2)~(6)式仿真得到节点接收端的掠射角αN。在节点测得接收端掠射角情况下, 利用本文提出的定位方法, 先通过基于掠射角的声线修正方法得到声线经过的水平距离, 然后采用微分迭代定位方法计算得到UUV的位置。

本文主要针对深海UUV进行水声定位, 因此选用Munk声速剖面, 如图 4所示, 水深为5 000 m。

thumbnail 图4

Munk声速剖面

本文所提算法的性能用均方根误差(root mean square error, RMSE)和偏差这2个指标进行评价。

对于单个节点，节点和UUV间声线传播水平距离估计的RMSE为

式中：ro为节点和UUV间声线传播水平距离的真实值; rk为第k次仿真实验的水平距离估计值; L为蒙特卡洛仿真实验的次数。

对于UUV位置估计，RMSE和偏差(bias)分别为

式中，u k为第k次仿真实验的目标估计位置; L为蒙特卡洛仿真实验的次数。

3.1 声线传播时间测量值误差对传统声线修正方法性能影响的仿真及分析

当节点和UUV间时钟异步时, 声线传播时间的测量值就会存在误差。当声线传播时间的测量值存在误差时, 传统声线修正方法的效果会受到影响。在传统声线修正方法中, 查表法可以根据迭代法建立表格, 有效声速可以通过(2)~(6)式仿真的声线传播时间计算得到。因此对有效声速法和迭代法的修正效果进行仿真。

仿真中, 节点位置坐标为(50, 100, 35)m, UUV位置坐标为(1 000, 800, 1 000)m。当传播时间测量值无误差和误差方差为0.000 5, 0.001, 0.002, 0.003, 0.004, 0.005 s2时, 蒙特卡洛仿真实验的次数为5 000, 有效声速法和迭代法修正方法的效果如图 5所示, 其中图 5b)是图 5a)的局部放大。

thumbnail 图5

传播时间测量值误差对传统声线修正方法效果的影响

在图 5中, 当传播时间测量值无误差时, 迭代法计算的声线传播水平距离估计RMSE为0.074 3 m, 原因在于(2)~(6)式仿真的声线传播时间是近似精确的, 之后又以这个传播时间进行声线修正, 况且声速剖面也近似成N层等声速梯度分布, 所以声线修正得到的水平距离和真实水平距离之间有误差, 但误差很小, 可以忽略; 有效声速法在传播时间测量值和有效声速无误差时, 水平距离估计的RMSE为0。这些验证了传播时间无误差时传统声线修正方法的可行性。在图 5b)中, 传播时间测量值无误差时, 有效声速误差的方差越大, 有效声速法计算的声线传播水平距离的RMSE越大。

当传播时间测量值误差方差为0.000 5 s2时, 迭代法和有效声速法计算的声线传播水平距离的误差RMSE都在40 m以上, 随着误差方差的逐渐增大, 对应的RMSE也逐渐增大。可以看出, 当传播时间测量值误差存在时, 即使再小的传播时间测量值误差, 采用传统的声线修正方法也会产生很大的距离误差, 进而使UUV水声定位误差增大。因此当节点和UUV时钟异步时, 传统声线修正方法不再适用。

3.2 基于掠射角声线修正的深海UUV免时钟同步定位方法的性能仿真及分析

当节点和UUV间时钟异步时, 节点可测得声线的接收端掠射角, 比较基于时间的传统声线修正方法和本文提出的基于掠射角声线修正的深海UUV免时钟同步定位方法的性能。

仿真中, 传感器节点有6个, 节点位置坐标依次为 s 1=(50, 100, 35)m, s 2=(103, 600, 22)m, s 3=(500, 670, 30)m, s 4=(620, 300, 40)m, s 5=(400, 60, 20)m, s 6=(280, 390, 18)m。通过(2)~(6)式得到声线从UUV到每个节点的真实接收掠射角和声线传播时间。假设时钟异步导致的声线传播时间测量值误差的方差为0.000 5 s2, 有效声速值无误差, 然后分别通过这2种传统声线修正方法和本文提出的基于掠射角的声线修正方法得到声线经过的水平距离, 再采用最小二乘方法计算出UUV的位置, 对比3种方法修正的水平距离和定位效果。声线方向以水平轴为零度, 朝水平轴上方时, 掠射角为负, 垂直向上的掠射角为-90°; 朝向下方时, 掠射角为正, 垂直向下的掠射角为90°。

从图 4的Munk声速剖面图可以看到, 声速剖面大致可分为2段, 上半段是负梯度声速, 下半段是正梯度声速, 为了验证本文提出的基于掠射角的声线修正方法适用于各种声速分布, 仿真中让UUV分别处于负梯度声速和正梯度声速的深度上。UUV位置的水平坐标为(1 000, 800)m, 深度分别为600 m和2 700 m, 仿真结果分别如表 1~2所示。

表1

负梯度声速段声线修正和UUV定位效果

表2

正梯度声速段声线修正和UUV定位效果

表 1中, 传播时间测量值误差方差为0.000 5 s2时, 采用基于时间的传统声线修正方法中的迭代法和有效声速法进行修正, 水平距离估计的均方误差均在30 m以上, 利用得到的水平距离进行定位, 势必会带来很大的定位误差。然而利用接收端掠射角采用本文提出的基于掠射角的声线修正方法, 水平距离误差均在1 m以下。最后采用最小二乘方法进行求解, 得UUV位置的水平坐标为(1 000.52, 799.52)m, 结合UUV已知的深度, 可得UUV位置的三维坐标为(1 000.52, 799.52, 600)m。表 2中, 可以看到类似的结果, 最终求得UUV位置的三维坐标为(1 000.24, 800.48, 2 700)m。

从以上的仿真结果分析可以看出, 当时钟异步时, 基于时间的传统声线修正方法得到的水平距离误差很大, 已经不能满足定位中对于距离精度的要求, 而本文提出的基于掠射角的声线修正方法效果很好, 水平距离误差均在1 m以内, 能够很好地修正声线弯曲对UASN深海UUV水声定位带来的影响, 提高定位精度, 验证了在掠射角无误差情况下基于掠射角声线修正的深海UUV免时钟同步定位方法的可行性。

3.3 掠射角测量值存在误差时方法性能仿真及分析

本文提出了基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法, 在声线修正部分, 传感器节点需要测得声线的掠射角, 实际设计中每个节点可以配置垂直线列阵, 通过波达方向估计方法估计入射信号的到达角, 进而得到声线的掠射角。但在实际中, 波达方向估计方法、阵列倾斜等都会使入射信号到达角度估计不准确, 声线掠射角估计也就会存在误差。

3.3.1 基于掠射角声线修正方法的水平距离修正效果仿真及分析

本小节在掠射角测量值存在误差情况下, 仿真深海UUV位于不同位置时基于掠射角声线修正方法的水平距离估计误差的变化情况, 并进行分析。

仿真分为两部分: 水平距离一定时, UUV深度逐渐增大; UUV深度一定时, 水平距离逐渐增大。仿真中, 掠射角测量误差服从零均值、方差为σα2的高斯分布, 蒙特卡洛仿真实验次数为5 000。

1) 水平距离一定时, UUV深度逐渐增大。

节点深度为35 m, UUV与节点间水平距离不变, UUV深度从600 m增加到2 600 m。仿真中, 掠射角测量误差的方差分别为0.5, 1.0, 1.5, 2.0 (°)2, 仿真结果如图 6所示, 其中图 6a)对应的水平距离为1 000 m, 图 6b)对应的水平距离为1 600 m。

thumbnail 图6

掠射角测量误差存在时水平距离估计误差随深度变化情况

图 6中, 当水平距离和目标深度固定时, 掠射角测量误差越大, 水平距离估计误差就越大; 对于同一个测量值误差方差, 在水平距离一定时, 随着目标深度的增加, 水平距离估计误差的RMSE先减小、后增大, 图 6a)在1 000 m左右深度处取得最小值, 图 6b)在1 600 m左右深度处取得最小值。图 4的Munk声速剖面中, 声速曲线是先下降后上升, 为了验证图 6的水平距离估计误差变化是否与图 4声速曲线变化相关, 将接收节点深度设置为1 600 m, UUV与节点水平距离为800 m, 仿真结果如图 7所示。

thumbnail 图7

节点处于正声速梯度、掠射角测量误差存在时水平距离估计误差随深度变化情况

图 7中, 水平距离估计误差的RMSE也是先减小、后增大, 可见掠射角测量误差存在时水平距离估计误差的先减小后增加变化与节点和UUV所处声速层无关; 同时可以看到, 水平距离估计误差的RMSE最小值在2 400 m左右UUV深度处。分析图 6~7可以得出, 水平距离一定时, UUV和接收节点之间的深度差与水平距离相差越大, 水平距离估计误差越大; 当两者相等时, 水平距离估计误差最小。

2) UUV深度一定时, 水平距离逐渐增大。

节点深度为35 m, UUV深度为1 000 m, 水平距离从250 m增加到5 000 m。仿真中, 掠射角测量误差的方差分别为0.5, 1.0, 1.5, 2.0 (°)2, 仿真结果如图 8所示。

thumbnail 图8

掠射角测量误差存在时水平距离估计误差随水平距离变化情况

图 8中, 掠射角测量误差越大, 水平距离估计误差也越大; 在UUV深度一定时, 水平距离估计误差随水平距离的增大而增大, 水平距离越大, 水平距离估计误差也越大。

UASN可以对目标直接进行定位, 也可以作为UUV惯性导航等定位方式的辅助, 图 6~8得出的结论对于节点深度设置、通信范围内节点选择及定位时UUV所处深度的选取有实际的指导意义。同时可以看到, 为了根本上提高水平距离估计精度, 提高信号入射角估计精度是今后研究的一个重要方向。

3.3.2 基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法的性能仿真及分析

仿真中, 传感器节点与3.2节的节点设置一样, UUV位置的坐标为(1 000, 800, 600)m, 假设掠射角测量误差服从均值为零、方差为σα2的高斯分布, 比较基于掠射角声线修正后直接利用最小二乘方法和利用微分迭代方法进行UUV定位的效果。将基于掠射角声线修正后直接利用最小二乘方法估计的方法表示为“掠射角声线修正-最小二乘方法”, 将本文提出的基于掠射角声线修正后利用微分迭代方法估计的方法表示为“掠射角声线修正-微分迭代方法”。

图 9展示了掠射角声线修正-最小二乘方法和掠射角声线修正-微分迭代方法2种方法的100次定位结果分布。图中, 红色实心点表示UUV的真实位置, 图 9a)的蓝色空心正方形表示掠射角声线修正-最小二乘方法的估计结果, 图 9b)的蓝色空心五角星表示掠射角声线修正-微分迭代方法的估计结果。仿真中, σα2=2 (°)2。从图 9中可以看到, 掠射角声线修正-最小二乘方法的估计结果距离真值较远且比较分散, 掠射角声线修正-微分迭代方法的估计结果在真值附近且比较集中, 直观上看, 掠射角声线修正-微分迭代方法估计的偏差低于掠射角声线修正-最小二乘方法估计的偏差。

thumbnail 图9

UUV定位结果x-y平面分布图

图 10展示了σα2从0.5~3 (°)2变化时2种方法的定位性能。图 10a)是RMSE结果, 2种方法估计误差的RMSE都随着σα2增大而增大, 本文提出的掠射角声线修正-微分迭代方法估计误差的RMSE明显小于掠射角声线修正-最小二乘方法估计误差的RMSE。图 10b)是偏差结果, 2种方法估计误差的偏差都随着σα2增大而增大, 本文提出的掠射角声线修正-微分迭代方法的估计误差偏差小于掠射角声线修正-最小二乘方法的估计误差偏差。

thumbnail 图10

掠射角测量值误差对基于掠射角声线修正的目标定位方法的性能影响

图 10的仿真结果表明, 本文提出的掠射角声线修正-微分迭代方法的估计误差RMSE和偏差都小于掠射角声线修正-最小二乘方法估计误差的RMSE和偏差, 所以本文提出的掠射角声线修正-微分迭代方法的定位效果优于掠射角声线修正-最小二乘方法的定位效果, 明显修正了掠射角测量值误差对深海UUV水声定位的影响。

4 公开数据集验证

采用国家海洋科学数据中心的西北太平洋中国海洋实况分析(CORTA 1.0-WNP)-声速数据集对本文所提方法进行Bellhop模拟验证。CORTA 1.0-WNP采用国家卫星海洋应用中心及国际公开的海表温度和海面高度数据重构水下三维温盐场, 并利用国际公开和中心观测监测的实时/准实时资料对重构场进行同化订正, 产品的海区范围为99°E~150°E、10°S~52°N, 空间水平网格分辨率为0.125°。Bellhop模型是水声信道计算与仿真中应用最为广泛的模型之一, 该模型通过对声场模型进行计算可得到传播损失、本征声线、冲激响应以及声线到达时间序列等多种实用数据, 是声场建模及分析的一种有效手段。

该数据集中, 海洋深度0~9 000 m, 共有51个深度层边界。在同一个深度层边界上, 海区范围内每个网格的声速值略有差异, 部分网格没有声速数据。因此, 要对数据集的数据进行处理, 首先对同一深度层边界上的非NaN数据进行平均操作, 得到表 3所示的分层声速数据。然后再对分层声速值进行3次样条插值, 得到如图 11的声速剖面。

表3

某海域分层声速数据

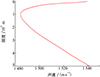thumbnail 图11

某海域声速剖面

将6个节点分别布放于实验海域某区域, 在三维直角坐标系中, 节点位置与3.2中节点位置一样。目标在(1 000, 800, 600)m处发射定位信号, 6个节点分别接收到目标发射的信号。用Bellhop模型分别模拟声线的传播路径, 计算出各节点接收处直达径声线的掠射角, 如表 4所示。

表4

各节点处声线掠射角

在实际海域实验时, 垂直线列阵测量的掠射角会存在误差。假设节点接收处掠射角测量值误差服从均值为零、方差σα2=1(°)2的高斯分布, 仿真本文所提基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法, 仿真次数为5 000, 计算出目标到各节点的水平距离误差RMSE, 结果如表 5所示。目标位置估计误差RMSE为44.65 m。

表5

公开数据集模拟定位结果

图 12是模拟定位结果的x-y平面分布图, 蓝色区域是5 000次估计的目标位置分布范围。

thumbnail 图12

模拟定位结果x-y平面分布图

表 5中, 在节点接收处掠射角测量值误差方差σα2=1(°)2时, 采用本文提出的方法计算出目标到各节点的水平距离和目标位置, 水平距离RMSE在50 m以下, 目标位置估计RMSE为44.65 m。图 12中, 蓝色区域集中围绕在目标真实位置的红色实心圆点周围。对表 5和图 12进行分析, 可以得出, 在实际实验时掠射角测量值存在误差的情况下, 本文提出的基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法可以高精度地估计出UUV的位置。

5 结论

本文针对UASN深海UUV水声定位中UUV、节点间时钟异步和声线弯曲问题, 提出了一种基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法。在节点和UUV间时钟异步时, 该方法可以通过节点测得的接收掠射角, 获得精确的UUV和节点间水平距离, 针对掠射角测量值存在误差情况采用微分迭代方法提高UUV的定位精度。Matlab仿真和Bellhop模拟实验验证了方法的可行性和有效性, 表明本文提出的基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法可以使UASN深海UUV水声定位的精度更高, 同时在掠射角测量误差存在时仿真了基于掠射角的声线修正效果, 对实际定位中节点深度设置和通信范围内节点选择具有一定的指导意义。

由于深海目标的声线类型简单, 声线数量少, 本文针对节点接收的直达径声线进行研究, 提出了一种基于掠射角声线修正及微分迭代的深海UUV免时钟同步定位方法。下一步将针对声线存在反转点和海面海底反射的情况进行研究, 研究声线类型的区分方法及相应的声线修正和定位方法。

References

  1. JIA Tianyi, GAO Jingjie, SHEN Xiaohong, et al. Moving underwater vehicle localization with uncertain sound speed[J]. Systems Engineering and Electronics, 2022, 44(9): 2699–2706 (in Chinese) [Google Scholar]
  2. JIA Tianyi, HO K C, WANG Haiyan, et al. Localization of a moving object with sensors in motion by time delays and doppler shifts[J]. IEEE Trans on Signal Processing, 2020, 68(1): 5824–5841 [Google Scholar]
  3. SUN Dajun, ZHENG Cui'e, CUI Hongyu, et al. Developing status and some cutting-edge issues of underwater sensor network localization technology[J]. Scientia Sinica Informationis, 2018, 48(9): 1121–1136 (in Chinese) [Google Scholar]
  4. ZHAO Chen, QIAO Gang, ZHOU Feng. Underwater cooperative target localization method based on double orthogonal moving autonomous underwater vehicles[J]. Journal of Electronics & Information Technology, 2021, 43(3): 834–841 (in Chinese) [Google Scholar]
  5. JIA Tianyi, WANG Haiyan, SHEN Xiaohong, et al. Target localization based on structured total least squares with hybrid TDOA-AOA measurements[J]. Elsevier Signal Processing, 2018, 143(1): 211–221 [Google Scholar]
  6. WANG Ling, SHEN Xiaohong, KANG Yuzhu, et al. Least squares estimation performance for TDOA target localization in underwater acoustic sensor networks[J]. Acta Armamentarii, 2020, 41(3): 542–551 (in Chinese) [Google Scholar]
  7. GONG Zijun, LI Cheng, JIANG Fan. AUV-aided joint localization and time synchronization for underwater acoustic sensor networks[J]. IEEE Signal Processing Letters, 2018, 25(4): 477–481 [Google Scholar]
  8. LUO Junhai, YANG Yang, WANG Zhiyan, et al. Localization algorithm for underwater sensor network: a review[J]. IEEE Internet of Things Journal, 2021, 8(17): 13126–13144 [Google Scholar]
  9. LUO J H, FAN L Y, WU S, et al. Research on localization algorithms based on acoustic communication for underwater sensor networks[J]. Sensors, 2018, 18(1): 67 [Google Scholar]
  10. GAO Ruru, XU Tianhe, AI Qingsong. Research on underwater sound velocity calculation, error correction and positioning algorithms[C]//CPGPS 2017 Forum on Cooperative Positioning and Service, Harbin, 2017 [Google Scholar]
  11. ZHAO Shuang, WANG Zhenjie, HE Kaifei, et al. Investigation on underwater positioning stochastic model based on acoustic ray incidence angle[J]. Applied Ocean Research, 2018, 77: 69–77 [Google Scholar]
  12. ZHENG Cui'e, CHENG Chiyu, HAN Yunfeng, et al. Medium and remote range acoustic PNT datum positioning and navigation technology[J]. Journal of Harbin Engineering University, 2023, 44(11): 2018–2026 (in Chinese) [Google Scholar]
  13. AMEER P M, JACOB L. Underwater localization using stochastic proximity embedding and multi-dimensional scaling[J]. Wireless Networks, 2013, 19(7): 1679–1690 [Google Scholar]
  14. GONG Haoliang, CHEN Bo, WAN Lili, et al. A dichotomy iteration method of real-time sound ray correction[J]. Technical Acoustics, 2018, 37(4): 303–308 (in Chinese) [Google Scholar]
  15. LIANG Minzan, YU Yi, WANG Liming, et al. A table look-up method of sound ray correction[J]. Technical Acoustics, 2009, 28(4): 556–559 (in Chinese) [Google Scholar]
  16. LIN Wangsheng. Research on underwater sound channel simulation and sound ray revision[D]. Harbin: Harbin Engineering University, 2009 (in Chinese) [Google Scholar]
  17. SUN D J, LI H P, ZHENG C E, et al. Sound velocity correction based on effective sound velocity for underwater acoustic positioning systems[J]. Elsevier Applied Acoustics, 2019, 151(1): 55–62 [Google Scholar]
  18. DUAN Rui. Studies on sound propagation and source localization methods in deep water[D]. Xi'an: Northwestern Polytechnical University, 2016 (in Chinese) [Google Scholar]

All Tables

表1

负梯度声速段声线修正和UUV定位效果

In the text
表2

正梯度声速段声线修正和UUV定位效果

In the text
表3

某海域分层声速数据

In the text
表4

各节点处声线掠射角

In the text
表5

公开数据集模拟定位结果

In the text

All Figures

thumbnail 图1

UASN目标定位原理示意图
In the text
thumbnail 图2

分层介质模型的声速和声线图

1
In the text
thumbnail 图3

节点垂直线列阵测向示意图
In the text
thumbnail 图4

Munk声速剖面
In the text
thumbnail 图5

传播时间测量值误差对传统声线修正方法效果的影响
In the text
thumbnail 图6

掠射角测量误差存在时水平距离估计误差随深度变化情况
In the text
thumbnail 图7

节点处于正声速梯度、掠射角测量误差存在时水平距离估计误差随深度变化情况
In the text
thumbnail 图8

掠射角测量误差存在时水平距离估计误差随水平距离变化情况
In the text
thumbnail 图9

UUV定位结果x-y平面分布图
In the text
thumbnail 图10

掠射角测量值误差对基于掠射角声线修正的目标定位方法的性能影响
In the text
thumbnail 图11

某海域声速剖面
In the text
thumbnail 图12

模拟定位结果x-y平面分布图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.